现在的浇梁板体系都是梁和板共同工作, 一般将框架梁看成T型梁, 将梁和板分别称为腹板和翼缘板。

对于T型梁, 一般其挠度ω (x)和沿着梁轴线方向的位移μ (x, y)分别为:

ω=ω(x)(1)μ(x, y)=hudwdx+1-y3b3u(x)2

式中:u(x)为板剪切变形的最大差值; b为1/2的板净跨; h_u为截面的形心轴到翼缘板的中面距离。

通过理论推导可以得到:

EIw″+M(x)+34EIuu'(x)=0(3)EIu-914u″(x)-34w‴+95Gu(x)Eb2=04EIu914u'(x)-34w″δu(x)x1x2=0(5)

式中:E为弹性模量; I为抗弯系数; M(x)为弯矩; u(x)为板剪切变形的最大差值; G为剪切模量; b为板的跨度。

式(3)(4)(5)就是剪力滞后的基本微分方程。令:

n=11-78IuI; k=1b14Gn5E

式中:n和k分别为Reissner系数, 推导可得:

μ″(x)-k2u(x)=7nQ(x)6EI6

式中:Q(x)为横向截面的剪力表达式, 式(6)的解为:

μ(x)=7n6EI(c1ekx+c2e-kx+μ* )(7)

式中:μ ^* 是与Q(x)分布较为相关的特解; 系数c₁和c₂一般通过边界条件确定。

由图1可以计算得到该截面梁的内力为:

M(x)=12qlx-M0-112ql2-12qx27

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 混凝土梁隔离体的计算简图Fig.1 Calculation diagram concrete beam separator

式中:M₀=F_e是由于预应力偏心产生的弯矩;

σmax=huI(M0-124ql2)-7nq6k2·3Iu4Ilkekl21-ekl+18

σ _max一般出现在梁肋以及翼板相互交接的地方, 也就是y=b的地方。

Be=b1-1M0q-124l2·8k27n·1-ekllkekl2+1-ekl+IuI9令:K1=M0q-124l2; K2=8k27n·1-ekllkekl2+1-ekl10K3=IuI11

因此, 梁跨中的有效翼缘宽度为:

Be=1-1K1K2+K3b12

式中:K₁为荷载; K₂的值取决于材料的性质以及几何性质; K₃是翼缘板的惯性矩和总截面惯性矩的比值。

在实际工程中, 如果梁或者板的截面尺寸、材料的性质以及支座情况等参数确定之后, 三个参数K₁、K₂、K₃就比较容易求出。

GB 50010-2002的7.2.3款规定:T形、I形及以及倒L形截面受弯构件的受压翼缘宽度b'_f一般都应该按照规范中的最小值进行确定。这个规定特别适用于计算预应力混凝土的受弯构件正截面的承载能力极限状态, 这样, 预应力混凝土梁板体系有效翼缘的宽度在受弯极限承载力下有具体规定, 但是如果是在弹性状态下规范就没有给出相应的规定。

美国ACI318-02规范中对有效翼缘取值也有特别规定:如果将预应力混凝土板看成T形梁翼缘, 其有效宽度要小于或者等于梁跨度的1/4, 并且预应力混凝土梁腹的两侧悬出翼缘的有效宽度是预应力混凝土板厚的8倍或者相邻预应力混凝土梁净距的1/2。如果近一侧有混凝土板的预应力混凝土梁, 悬挑出来的有效宽度是预应力混凝土梁跨度的1/12或预应力混凝土板厚度的6倍或相邻混凝土梁腹之间净距的1/2。

MC90模式规范对预应力混凝土梁有效翼缘的宽度也进行了规定:预应力混凝土梁有效宽度可以在弹性或者塑性理论计算的基础进行确定, 预应力混凝土梁有效宽度可以沿着梁的轴线发生变化。如果没有确定预应力混凝土梁有效宽度时, 一般用于进行总体分析的预应力混凝土梁有效宽度可以取腹板厚度(h)加上零弯矩点之间距离l₀的1/5, 但是要注意的一点是不可以超过预应力混凝土梁顶板的实际宽度h₀。在这样的情况下, 预应力混凝土梁的有效宽度沿着这个跨度的方向可以取为常数, 包括了连续预应力混凝土梁接近中间支座的地方。对于预应力混凝土的边梁, 有效宽度的值等于腹板厚度h加上零弯矩点之间距离的十分之一。如果相邻跨度的比率为1~1.5, 且预应力混凝土悬臂部分的长度(l₁)不大于邻跨的1/2时, 设计算跨度为l, 则各跨的零弯矩之间距离l₀的取值为:预应力混凝土端跨为0.85l; 预应力混凝土中间跨为0.7l; 预应力混凝土悬臂跨为2l。

T形预应力混凝土梁有效翼缘宽度的取值不但要考虑腹板尺寸、翼缘尺寸以及跨度, 而且还要考虑预应力混凝土梁的一些支座条件。美国规范ACI318指出混凝土梁有效翼缘宽度取值是针对非预应力的混凝土梁所提出来的, 规范并没有考虑不同形式的荷载所采用的应力之间的区别, 尤其是忽略了受弯作用以及受轴压作用两者之间的区别。

黄坤耀等^[4]针对某个实际的工程案例, 采用有限元分析方法分析了有粘结的预应力混凝土梁板柱体系, 得出相应的应力分布基本情况, 结果表明:影响预应力混凝土梁有效翼缘宽度的一个很重要的因素就是结构受力类型, 翼缘在等效轴力作用下(主要是由预应力产生), 其应力分布曲线相对比较平坦, 预应力混凝土梁的有效翼缘宽度较宽。Aalami^[5]通过试验研究分析得出相似的结论。对于单跨预应力框架梁, 在预应力等效荷载的作用下, 预应力混凝土翼缘板将会出现压应力, 而且这种应力会迅速地从端部扩展到跨中, 最后基本达到均匀分布; 但在等效的均布荷载以及集中弯矩的作用下, 预应力混凝土翼缘板跨中的压应力分布不是很均匀, 最大的应力发生在板梁相交处, 随着远离梁的距离的不断增大, 应力越来越小。预应力混凝土翼缘板梁板在受弯的时候, 通常翼缘的肋梁上方位置相对其他位置具有较大的受力, 而且预应力混凝土翼缘内部的纵向压应力会随着离梁的远近程度而发生不同的变化。产生这种翼缘压应力变化的主要原因是由于预应力混凝土翼缘内的剪切滞后的影响, 由于存在着剪切变形, 纵向压应变与梁距离呈现负相关的关系。如果仅仅受轴向力的作用, 剪切滞后效应不会存在, 从而预应力混凝土梁跨中的压应变也相对较为均匀。

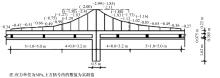
河北省的一新客站广场工程位于河北省火车站的南侧, 该结构采用的是连续多跨双向预应力的框架结构, 地面以上是3层, 地下1层, 地上的第2层的梁为连续三跨连续梁, 跨度达到了15 m, 由于该大跨度的连续梁要承受结构上面柱子的自重以及较大的荷载, 设计的时候采用后张法进行预应力施工, 第2层的预应力梁的配筋图如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 预应力混凝土梁的预应力配筋图Fig.2 Prestressed reinforcement figure of prestressed concrete beams

第2层楼板主要包括了两种类型的混凝土板:一种是厚度为200 mm的单层板; 另外一种是上层板厚度为220 mm, 下层板厚度为80 mm的双层板, 预应力混凝土梁的截面在单层楼板的宽和高分别是480 mm和1600 mm, 而在双层混凝楼板的宽和高分别是480 mm和2000 mm。所采用预应力钢筋是低松弛的钢丝束, f_ptk=1800 MPa, 其进行张拉时的控制应力取为1438 MPa, 张拉的方式采用两段张拉, 而且所采用的混凝土的等级为C40。这是一个典型的跨度较大的双向梁板柱结构, 在进行框架计算时, 楼板对梁的弯曲刚度不能忽略。

本文采用有限单元方法确定预应力混凝土梁的有效翼缘宽度, 并将计算结果与现场的实测结果进行对比分析。

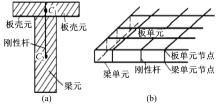
图3为梁、板单元相连的刚性杆。图中, C₁、C₂分别为梁和板的形心。由图3可以得出, 预应力混凝土梁的计算应该分别按照T形以及矩形取值, 计算得到的结果相差不是很大, 由图4可知, 预应力混凝土翼缘上面的纵向应力的分布相对混凝土梁的中部区域而言不是很均匀, 距离梁较近的位置应力较大, 而距离梁较远的地方应力较小。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 梁、板单元相连的刚性杆Fig.3 Liang, rigid rod plate unit connected

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 2-2截面的应力分布图Fig.4 Stress distribution of 2-2 sectional

某一个桥梁工程的单幅宽度是15.5 m, 这座桥是跨越永定新河的一座特别大的桥, 单幅的桥宽达到16.5 m。由于该桥的长度较长, 超过了1000 m, 而且与永定新河呈45° 的交角, 为了更好地进行施工, 采用三联3× 55 m PZ造桥机施工形成预应力混凝土连续箱梁, 平曲线的半径达到了5000 m。施工的第1阶段是简支的单悬臂, 施工长度为55 m简支加11 m悬臂, 该桥设计的悬臂尺寸为跨径长度的1/5, 从力学角度来讲, 该位置的弯矩最小, 所以将施工缝设在该位置; 施工的第2阶段完成长度为44 m加11 m悬臂; 施工的第3阶段完成剩下的44 m。采用的主要预应力钢束都是单向张拉的方式, 而且最大单向的张拉长度达到66 m。按预应力混凝土采用C50。基本参数如下:E_c=3.45× 10⁴ MPa; f_cd=22.4 MPa; f_td=1.83 MPa。

预应力钢绞线的基本参数为:

E_p=1.95× 10⁵ MPa; f_pk=1860 MPa, f_pd=1260 MPa。

HRB335级钢筋的基本参数为:

E_s=2.00× 10⁵ MPa; f_sd=280 MPa; f_sd=280 MPa

3.3.1 预应力混凝土翼缘有效宽度的计算

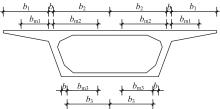
当箱形截面预应力混凝土梁承受弯矩作用的时候, 在横桥的方向会存在剪力滞后效应, 这样接近腹板的翼缘的法向应力就会与腹板法向应力较为接近, 且离预应力混凝土腹板距离越大则法向应力越小。在进行预应力施工过程中, 所有的预应力钢束都应该布置在预应力混凝土翼缘的有效宽度以内, 这样可以保证预应力混凝土能够均匀受力, 在进行设计和计算的时候认为分布在预应力混凝土翼缘有效宽度范围以内的普通钢筋能够有效地发挥作用。图5为箱梁的截面尺寸。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 箱梁的截面尺寸Fig.5 Box girder cross-sectional dimension

对于预应力混凝土梁的边支点以及边跨中的梁段L_i=0.8L=44 m; 对于预应力混凝土梁跨中梁段L_i=0.6L=33 m, 中间支点的L_i等于0.2倍的两个相邻跨径的和, 即L_i=0.2× (55+55)=22 m。

(1)计算应力混凝土梁中支点的翼缘的等效宽度:

悬臂板:b₁/L₁=0.16, 查ρ -s曲线, b_m1/b₁=0.55, b_m1=0.55× 3.5 m=1.93 m

箱内顶板:b₂/L₂=0.17, 查ρ -s曲线, b_m2/b₂=0.5, b_m2=0.5× b₂=1.92 m

箱内底板:b₃/L₃=0.13, 查ρ -s曲线, b_m3/b₃=0.65, b_m3=0.65× 2.92 m=1.90 m

(2)计算预应力混凝土梁中跨跨中翼缘的等效宽度:

悬臂板:b₁/L₁=0.11, 查ρ -f曲线, b_m1/b₁=0.9, b_m1=0.9× 3.5 m=3.15 m

箱内顶板:b₂/L₂=0.13, 查ρ -f曲线, b_m2/b₂=0.86, b_m2=0.86× 4.38 m=3.77 m

箱内底板:b₃/L₃=0.10, 查ρ -f曲线, b_m3/b₃=0.92, b_m3=0.92× 3.31 m=3.05 m。全部的计算结果如表1所示。

表1

Table 1

表1(Table 1)

表1 翼缘有效宽度计算(m) Table 1 Effective flange width calculation (m) 计算位置 混凝土悬臂板 底板 底板箱内顶板 边部支点 b1 3.45 b3 2.84 B2 3.82 L1 44.24 L3 43.95 L2 43.98 b1/L1 0.08 B3/L3 0.06 B2/L2 0.09 Bm1/L1 0.74 Bm3/L3 0.89 Bm2/L2 0.82 Bm1 2.62 Bm3 2.54 Bm2 2.79 边跨的跨 中部位 b1 3.49 b3 3.32 B2 4.37 L1 43.98 L3 43.98 L2 43.98 b1/L1 0.08 B3/L3 0.08 B2/L2 0.09 Bm1/L1 0.94 Bm3/L3 0.94 Bm2/L2 0.93 Bm1 3.34 Bm3 3.13 Bm2 4.02 中部的 支点 b1 3.49 b3 2.93 B2 3.82 L1 21.98 L3 21.98 L2 21.98 b1/L1 0.15 B3/L3 0.12 B2/L2 0.16 Bm1/L1 0.54 Bm3/L3 0.66 Bm2/L2 0.49 Bm1 1.92 Bm3 1.89 Bm2 1.91 中跨的跨 中位置 b1 3.49 b3 3.32 B2 4.37 L1 32.98 L3 32.98 L2 32.98 b1/L1 0.12 B3/L3 0.11 B2/L2 0.12 Bm1/L1 0.89 Bm3/L3 0.91 Bm2/L2 0.88 Bm1 3.14 Bm3 3.04 Bm2 3.76

表1 翼缘有效宽度计算(m) Table 1 Effective flange width calculation (m)

通过对计算结果进行分析可得, 预应力混凝土的跨中翼缘的有效宽度的折减相对比较小, 但在预应力混凝土的支点的位置的折减比较大, 产生这种现象的原因是由于支点位置的剪力滞后效应较大。

3.3.2 预应力混凝土压应力的控制

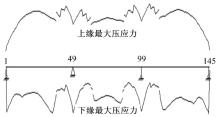
(1)预应力混凝土的正截面压应力的控制公式为:σ _pt+σ _kc≤ 0.5f_ck, 也就是要求本案例中的预应力混凝土的正截面压应力小于等于16.19 MPa。从图6可以看出, 预应力混凝土的最大压应力9.93 MPa大约在节点105的上缘位置, 基本满足要求。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 正截面混凝土压应力Fig.6 Normal section of concrete compressive stress

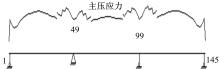
(2)预应力混凝土斜截面的主压应力的控制公式为:σ _cp≤ 0.6f_ck, 也就是要求本案例中的预应力混凝土的主压应力小于等于19.43 MPa。从图7可以看出, 预应力混凝土的最大主压应力为9.918 MPa, 大约在节点105上缘的位置, 满足要求。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 基本组合混凝土的主压应力Fig.7 Master the basic combination of concrete compressive stress

3.3.3 预应力混凝土钢筋拉应力控制

(1)预应力混凝土中的钢绞线的最大拉应力控制公式为:σ _pe+σ _p≤ 0.64f_pk, 也就是钢绞线的最大拉应力小于等于1208 MPa。

(2)预应力混凝土的最大拉应力1239 MPa> 0.65f_pk=1208 MPa, 通过计算可以看出, 只有局部的一个点的值略大, 在2.48%左右。详细的计算结果见表2。由表2可以得出, 对于预应力混凝土中的短钢束, 竖向弯矩较小的可以通过减小

表2

Table 2

表2(Table 2)

表2 钢束最大永存应力 Table 2 The maximum stress forever of steel beam 编 号 钢束 编号 预应力钢筋的 最大拉应力/Mpa 钢筋容许 拉应力/Mpa 超出标准的 范围/% 1 19 1229 1208 - 2 20 1240 1208 2.47 3 21 1234 1208 - 4 22 1219 1208 - 5 23 1223 1208 - 6 24 1234 1208 - 7 29 1234 1208 -

表2 钢束最大永存应力 Table 2 The maximum stress forever of steel beam

施工工程中的张拉控制应力进行解决, 即使张拉的控制应力为0.70f_pk, 钢束上面的永存的应力一般不会超过标准的要求。