本试验在英国GDS单向激振动力三轴试验仪上进行(见图1), 其测定的动应变范围为10^-4~10^-2。考虑到在试验过程中轴向荷载作用时活塞的运动会引起围压的波动, GDS动三轴试验使用了平衡锤技术, 保证试验过程中围压稳定不变。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 GDS动力三轴试验仪Fig.1 GDS cyclic triaxial test instrument

试验所用土样为某工程场地粘土, 其基本物理指标如表1所示, 采用击实法批量制备试样^[9]。先配成含水率为19%的土样, 并在限制蒸发条件下保持24 h以使土的含水率及结构均匀, 然后分层装模, 按设计要求的干密度将土夯实压密, 试样尺寸为39.1 mm× 80 mm的圆柱体。

表1

Table 1

表1(Table 1)

表1 试验用土的物理指标 Table 1 Tests with soil physical indicators 天然含水率/% 土粒比重 液限% 塑性指数 颗粒组成/% 0.5~0.075 mm 0.075~0.005 mm < 0.005 mm 19.0 2.74 57.7 23.9 1.3 49.9 48.8

表1 试验用土的物理指标 Table 1 Tests with soil physical indicators

试验研究了粘土试样分别在不同固结围压、固结比及不同振动频率状态下的动力特性, 具体的试验方案如表2所示。对于每一个试样, 待固结变形稳定后, 向试样施加等幅正弦波荷载, 采用对同一试样逐级加大动应力的分级试验方法。土在循环动力荷载作用下会产生残余变形^{[10, 11]}, 而且产生残余变形的过程是不均匀的, 随循环次数的增加而逐渐减小。由于残余变形的影响, 在每一级动荷载下求得的一系列应力应变滞回圈并没有完全重合, 但在同级动应力作用下随着振动圈次的增加, 滞回圈趋于重合。

表2

Table 2

表2(Table 2)

表2 试验方案 Table 2 Experimental scheme 方案1 方案2 方案3 围压/kPa 频率/Hz 固结比 围压/kPa 频率/Hz 固结比 围压/kPa 频率/Hz 固结比 100 0.20 1.50 200 0.20 1.00 200 0.05 1.50 300 0.20 1.50 200 0.20 1.25 200 0.20 1.50 400 0.20 1.50 200 0.20 1.75 200 0.05 1.50

表2 试验方案 Table 2 Experimental scheme

图2为一个试样在某级动应力下振动75圈次的起始3圈次和最后3圈次, 可以看出在振动起始阶段土样产生的残余变形较大, 随着振动圈次的增加, 残余变形逐渐减小。表3列举了一系列滞回圈次的动力参数计算值, 可以看出残余变形对各个参数均有一定影响, 但是影响较小:第2圈次和第75圈次计算的动应变值相差约3.3%, 动弹模量相差约3.2%, 阻尼比相差约23%; 除阻尼比值相差较大外, 其他两项相差均较小。

表3

Table 3

表3(Table 3)

表3 计算数值 Table 3 Calculated values 圈次 2 5 10 40 60 70 75 动应变 4.12× 10-4 4.19× 10-4 4.20× 10-4 4.21× 10-4 4.25× 10-4 4.31× 10-4 4.26× 10-4 动弹模量/MPa 204.67 201.72 200.48 200.69 198.48 196.18 198.33 阻尼比/% 4.36 4.52 4.38 3.15 3.25 2.88 3.38

表3 计算数值 Table 3 Calculated values

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 滞回圈对比Fig.2 Contrast of hysteresis loop

试验过程中, 假如每一级动荷载均通过增加振动圈次消除残余变形的影响会造成孔压急剧上升, 也会影响最终的试验结果, 综合分析认为可以忽略残余变形对试验结果的影响。在本次试验研究中采取每级动荷载下振动3圈次的试验方法。

Hardin等^[5]由试验得出土在周期循环荷载作用下的应力-应变关系为双曲线型, 即:

σd=εd1Edmax+εdσdmax1

式中:E_dmax、σ _dmax分别为最大动弹模量和最大动应力。

式(1)亦可改写为:

Ed=1b+aεd2

各试验条件下的1/E_d-ε _d关系曲线均可以用直线来拟合, 直线斜率为a, 截距为b^{[12, 13, 14, 15, 16, 17]}, 其中:

Edmax=1/b3σdmax=1/a4

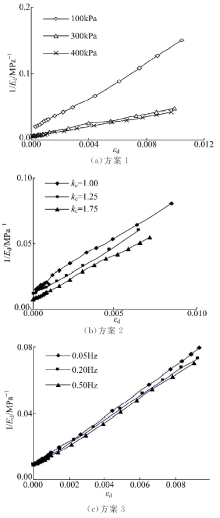
在坐标系下绘制不同试验条件下的1/E_d-ε _d关系曲线如图3所示。可以看出各试验条件下1/E_d与ε _d之间几乎呈线性关系, 可近似用直线方程进行描述。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 1/Ed-ε d关系曲线Fig.3 1/Ed-ε d curve

在土动力学中, 依据Janbu公式, 不论用固结压力σ ₃或平均主应力σ _m=(σ ₁+2σ ₃)/3(等压时k_c=1, σ ₃=σ _m), 均可以建立最大动弹模量E_dmax与平均主应力σ _m的指数关系式^{[18, 19, 20, 21]}:

Edmax=k·Pa·σm/Pan15

式中:Pa为大气压力; k、n₁为试验参数。

当k_c≠ 1时, 试件振动前承受了初始剪应力, 使土体骨架趋于更稳定结构。实践证明, 不同k_c的E_dmax-σ _m在双对数坐标系中不在一条线上。何昌荣^[8]采用动三轴试验对原状粘土和扰动砂土进行了较系统的动模量阻尼比试验, 考虑了固结比k_c的影响, 并提出了以下计算公式:

Edmax=k1·Pa·σ3/Pan2(kc)m6

式中:Pa为大气压力; k₁、n₂、m为试验参数。

在试验数据处理过程中, 针对本试验对式(6)进行了优化(用平均主应力σ _m代替σ ₃, 并根据试验经验取m=1), 得出如下计算公式:

Edmax=k1·Pa·(σm/Pa)n2·kc7

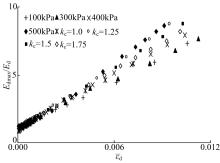
在双对数坐标系下绘制不同固结应力状态(σ ₃, k_c)下的(E_dmax/Pa· k_c)-(σ _m/Pa)关系曲线(见图4), 可见其表现出了良好的线性关系, 得到了在不同固结应力状态(σ ₃, k_c)下的归一化公式:

Edmax/Pa·kc=428.61·σm/Pa0.73928

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 (Edmax/Pa· kc)-(σ m/Pa)关系曲线Fig.4 (Edmax/Pa· kc)-(σ m/Pa)curve

为了验证式(8)的可靠度, 补充两个试验分别验证试验数据点内插与外延的计算精度, 试验方案如表4所示, 验证结果如表5所示。可以看出内插试验计算结果的可靠度超过了90%, 外延试验计算结果的可靠度超过了85%, 可靠度均较高。说明通过以上的处理方法来实现最大动弹模量E_dmax在不同固结应力状态(σ ₃, k_c)下的归一化是可行的。

表4

Table 4

表4(Table 4)

表4 补充试验方案 Table 4 Additional experimental scheme 编号 围压/kPa 频率/Hz 固结比 1 200 0.2 1.5 2 500 0.2 1.5

表4 补充试验方案 Table 4 Additional experimental scheme

表5

Table 5

表5(Table 5)

表5 Edmax值比较结果 Table 5 Comparison results of Edmax 编号 计算值/MPa 试验值/MPa 相差 1 120.3 129.4 7.1% 2 236.8 276.9 14.5%

表5 Edmax值比较结果 Table 5 Comparison results of Edmax

将式(7)代入式(2)中, 可得:

Ed=k1Pa(σmPa)nkc11+k1k2kcεd(σmPa)1-n9

式中:k₂=aσ _m。

移项并整理, 可得:

EdmaxEd=1+kεd¯10

式中:k=k₁· k₂。

εd¯=εdkc(σmPa)n-111

式中: εd¯称为归一化应变。

已知k₁、n₂的值, 绘制(E_dmax/E_d)与 εd¯之间关系曲线散点图(包括补充试验), 如图5所示。可见随着 εd¯的增大(E_dmax/E_d)呈现线性增长; 且经过归一化应变 εd¯的处理后, 不同固结应力状态(σ ₃, k_c)下的试验点均分布在较窄的范围内, 简化起见, 可以归一为一条直线。试验参数k₂的取值如表6所示, 可见k₂在不同的固结应力(k_c, σ ₃)状态下其值相差较小, 故可取其平均值, 即1.596, 则归一化直线表达式为:

EdmaxEd=1+684.06εd¯12

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 Edmax/Ed- εd¯关系Fig.5 Relation between Edmax/Ed and εd¯

表6

Table 6

表6(Table 6)

表6 参数k2取值 Table 6 Parameter k2 value 围压/kPa k2 固结比 k2 100 1.472 1.0 1.596 300 1.468 1.25 1.698 400 1.761 1.5 1.608 500 1.496 1.75 1.670

表6 参数k2取值 Table 6 Parameter k2 value

一般地, 阻尼比λ _d计算公式为滞回圈面积A₀和三角形面积A_T的比值:

λd=A04πAT13

Hardin等^[5]提出了几种砂性土和粘性土最大阻尼比λ _dmax的经验计算公式, 国内外其他文献也提出了一些求取方法和公式可供参考。依据大量试验和文献资料的分析发现, 应力应变水平较高以后(如ε _d> 5× 10^-4), 足够大的滞回圈可以较准确地确定λ _d, λ _d的变化和增幅也较小。λ _d-ε _d曲线的右上边趋于平缓, 渐近于某一常数, 取该渐近常数为 λdmax7。

由文献[7]可知动弹模量比R_E与动剪模量比R_G相等, 即:

RE=Ed/Edmax=Gd/Gdmax=RG14

Hardin等^[5]在根据试验资料对应力-应变滞回圈几何特征进行对比分析中发现, 卸载曲线的起始坡度总是等于或接近等于G_dmax, 而与应变幅大小无关^[18], 由此导出:

λd=λdmax1-GdGdmax15

为了使式(15)有更好的适用性, 有时在括号外再引入一个指数n₃, 写为^[18]:

λd=λdmax1-GdGdmaxn316

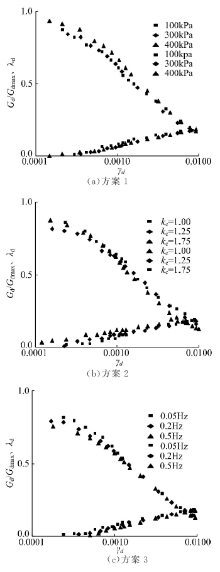
将各试验条件下的阻尼比λ _d-动剪应变γ _d与动剪模量比G_d/G_dmax-动剪应变γ _d关系曲线散点图绘制在单对数坐标系中(见图6)。由图6可以

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 λ d-γ d与Gd/Gdmax-γ d关系Fig.6 Relation between λ d and γ d, Gd/Gdmax and γ d

看出:

(1)各试验条件下阻尼比均随着动剪应变的增大而逐渐增大, 并逐渐趋于平缓; 在不同的固结围压及振动频率试验条件下, 数据点均集中在较窄的范围内, 为简便起见, 可以不考虑固结围压与振动频率对阻尼比的影响, 归一为一条曲线; 固结比对阻尼比有一定影响, 随着固结比的增加, 阻尼比曲线呈现跳跃式变化。

(2)不同试验条件下动剪模量比值均随着动剪应变的增大而减小, 且在不同试验条件下, 模量比关系曲线的试验点均分布在较窄的范围内:固结围压对其影响最大, 相差约10%左右, 固结比影响相差约15%左右, 振动频率影响相差约12%左右, 影响均较小。为简化起见, 认为在各个试验条件下动剪模量比关系曲线可以归一化处理。

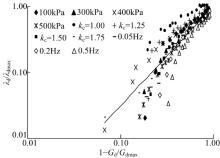
把不同试验条件下(包括补充试验)的(λ _d/λ _dmax)与(1-G_d/G_dmax)关系的试验点绘在同一对数坐标系中(见图7), 可以看出各试验条件下的试验点交错分布在较窄的范围内, 在一定精度范围内可以近似地归一为一条直线, 表达式为:

λd=λdmax1-GdGdmax1.508317

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 (λ d/λ dmax)-(1-Gd/Gdmax)关系Fig.7 Relation between(λ d/λ dmax) and (1-Gd/Gdmax)

由于不同试验条件下的λ _dmax值相差很小(求取过程略), 故取其平均值:0.2303。而由式(11)及式(14)可以得到以动应变ε _d或动剪应变γ _d为变量的动剪模量比函数, 这样阻尼比λ _d也就成为了动剪应变γ _d的函数, 便于计算。