负荷传感优先阀建模及仿真分析

引用本文

刘昕晖, 李倩雯, 陈晋市, 张鹏, 牛平杰. 负荷传感优先阀建模及仿真分析. 2015, 45(6): 1817-1824
LIU Xin-hui, LI Qian-wen, CHEN Jin-shi, ZHANG Peng, NIU Ping-jie. Mathematical modeling and simulation of load-sensing priority valve. Journal of Jilin University Engineering and Technology Edition, 2015, 45(6): 1817-1824 复制到剪切板

Permissions

负荷传感优先阀建模及仿真分析

刘昕晖^1,², 李倩雯¹, 陈晋市^1,³, 张鹏¹, 牛平杰¹

1.吉林大学机械科学与工程学院,长春 130022

2.吉林大学汽车仿真与控制国家重点实验室,长春 130022

3.广西柳工机械股份有限公司,广西柳州 545007

陈晋市(1983-),男,在站博士后.研究方向:流体传动与电液控制.E-mail:spreading@jlu.edu.cn

作者简介:刘昕晖(1962-),男,教授,博士生导师.研究方向:流体传动与电液控制.E-mail:liuxinhui8015@163.com

基金:湖南省科技重大专项项目(SW20120112)

摘要

介绍了某型号负荷传感静态优先阀的结构和工作原理,通过完整的数学模型和系统传递函数框图定性地分析了影响优先阀转向流量响应的重要参数,建立了其AMESim仿真模型,对优先阀在不同输入条件下的转向流量动态响应进行定量仿真分析,并对优先阀结构的关键参数进行了优化。对比仿真与实验结果发现,仿真模型准确反映了优先阀的输入输出特性。仿真分析表明,优先阀LS和R阻尼孔的大小对转向流量动态响应有很大影响,适当增大其直径可以提高系统性能。

关键词: 流体传动与控制; 全液压转向; 负荷传感; 优先阀; 动态特性; AMESim模型

中图分类号:TH137.5 文献标志码:A 文章编号:1671-5497(2015)06-1817-08

Mathematical modeling and simulation of load-sensing priority valve

LIU Xin-hui^1,², LI Qian-wen¹, CHEN Jin-shi^1,³, ZHANG Peng¹, NIU Ping-jie¹

1.School of Mechanical Science and Engineering, Jilin University, Changchun 130022, China

2.State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022, China

3.Guangxi LiuGong Machinery Co.,Ltd,Liuzhou 545007,China

Abstract

The structure and working principles of the load-sensing static signal priority vale are analyzed in this paper. By establishing the complete mathematical model and creating a block diagram of the system, the parameters, which have large impact on the steering flow response, are quantitatively analyzed, and the AMESim simulation model is established. The response of the steering flow under different input conditions is quantitatively investigated through dynamic simulation, and the key structure parameters are optimized. Comparison of simulation and experiment results shows that the model is accurate. Simulation results demonstrate that the sizes of the orifices of priority vale LS and damper S have huge influence on the response of the steering flow and increasing diameters appropriately can improve the system performance.

Keyword: fluid power transmission and control; full hydraulic steering system; load-sensing; priority valve; dynamic characteristic; AMESim model

Show Figures

转向系统的性能直接影响整机的安全性、工作效率、能源消耗等。目前, 采用铰接式转向的工程机械大都装配负荷传感全液压转向系统^[1], 而负荷传感优先阀是负荷传感全液压转向系统的核心元件, 其功能结构可等效为A型半桥回路, 流量增益较大, 阀芯移动较小的位移, 转向流量将产生大幅变化, 具有良好的动态特性。同时, 负荷传感优先阀与转向器组合使用, 不仅能根据转向速度的需要优先给转向系统供油, 又能保证转向器前后的压差保持恒定, 转向过程中转向速度不受转向负载和工作负载的影响, 保证转向供油流量的稳定性, 同时将剩余油液供给工作系统, 减少功率损失。该系统转向平稳可靠, 缺点是系统存在负荷传感油路及优先阀阀芯的响应时间, 有轻微的滞后感。

优先阀的转向流量动态响应对转向的平稳性和灵敏性有着重要的影响。但是以往研究鲜有对优先阀进行完整的数学模型搭建^{[2, 3]}, 且通常直接简化数学模型运用Simulink等软件仿真^[3]。本文针对负荷传感优先阀的工作原理和实际结构进行数学建模, 分析影响转向流量响应的重要参数, 并且按照优先阀的实际结构在AMESim液压元件设计库平台搭建模型进行仿真分析, 针对分析结果对优先阀结构参数提出优化方案。

1 优先阀结构及其工作原理

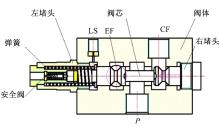
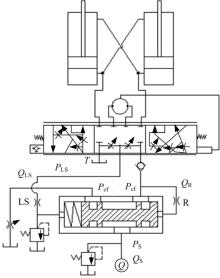
本文的研究对象是负荷传感静态优先阀, 其结构和组成如图1所示, 与开中心式全液压转向器组成全液压转向系统, 其液压原理图如图2所示。CF口接转向器P口; EF口接工作油路; LS负荷传感口与转向器LS口连接。

	Figure Option View Download New Window
	图1 优先阀结构图Fig.1 Structure of priority valve

	Figure Option View Download New Window
	图2 全液压转向系统液压原理图Fig.2 Hydraulic schematics of full hydraulic steering system

当系统开始工作, 液压泵向优先阀P口供油。转向器未转动时, 优先阀CF口、LS口和转向器T口通过转向器中位节流孔相联接。油液进入P-CF口, 由于转向器中位节流孔很小, CF口压力大于LS口压力, CF口压力通过R口反馈至阀芯右腔, LS口压力作用在阀芯左腔。优先阀阀芯左腔为低压腔, 因此阀芯左移, 大量油液从P-EF口进入工作系统, 只留少量油液经过P-CF口进入转向器中位阻尼孔产生压降, 来保持阀芯状态。

在转向器开始工作时, CF口经过转向器进油口与LS口相通, 油液流经P-CF口进入转向器。随着转向器转速的增加, 转向器进油口开口面积增大, CF口与LS口压差减小, 优先阀阀芯右移, P-CF口开大, CF口流量增大, CF口与LS口压差随之增加。因此, 通过动态调节使得CF口与LS口压差基本为一个定值, 而转向流量与转向器进油口大小成正比, 等于转向器转速乘以转向器计量马达排量^[4]。

当转向过程中, 外界负荷超过转向安全阀设定值时, LS口卸压, 此时流入转向系统的油液达到一恒定值, 转向速度不会再随着转向器开度的增大而增加。

2 优先阀数学模型

通过对转向器结构研究表明, 转向器阻尼孔在一定转向速度下为定值。LS口压力=转向负载压力+转向器内部阻尼孔压降(不包含转向器进口阻尼孔)。因此, 在对优先阀的动态性能研究过程中, 转向速度一定情况下, 用LS口压力可以衡量转向负载压力。优先阀各个节流口流量关系如下^[4]:

$\begin{matrix} \begin{matrix} Q_{S} = Q_{cf} + Q_{ef} (1) \\ Q_{cf} = Q_{1} + Q_{R} (2) \\ Q_{Z} = Q_{1} - Q_{LS} (3) \\ Q_{cf} = C_{d} A_{cf} \sqrt{2 (P_{S} - P_{cf}) / ρ} (4) \\ Q_{ef} = C_{d} A_{ef} \sqrt{2 (P_{S} - P_{ef}) / ρ} (5) \\ Q_{1} = C_{d} A_{Z} \sqrt{2 (P_{cf} - P_{LS}) / ρ} (6) \\ Q_{LS} = C_{d} A_{1} \sqrt{2 (P_{LS} - P_{L}) / ρ} (7) \\ Q_{R} = C_{d} A_{2} \sqrt{2 (P_{cf} - P_{R}) / ρ} (8) \\ A_{cf} = x_{cf} w_{cf} = (U_{cf} + x) w_{cf} (9) \\ A_{ef} = x_{ef} w_{ef} = (U_{ef} - x) w_{ef} (10) \\ A_{Z} = x_{Z} w_{Z} = (U_{Z} + x_{1}) w_{Z} (11) \end{matrix} \end{matrix}$

优先阀阀芯左右腔有:

$\begin{matrix} \begin{matrix} Q_{LS} - A_{f} \overset{\cdot}{x} = \frac{V_{1}}{β_{e}} \frac{d P_{L}}{dt} (12) \\ A_{f} \overset{\cdot}{x} - Q_{R} = \frac{V_{2}}{β_{e}} \frac{d P_{R}}{dt} (13) \end{matrix} \end{matrix}$

式中:Q_S为优先阀供油流量, L/min; Q_cf、Q_ef分别为优先阀CF口、EF口流量, L/min; Q₁为进入转向器流量, L/min; Q_R为优先阀流过R节流口A₂流量, L/min; Q_Z为流过转向器计量马达的流量, L/min; Q_LS为优先阀流过LS节流口A₁流量, L/min; C_d为流量系数; ρ 为液压油密度, kg/m³; A_cf、A_ef分别为CF、EF口通流面积, mm²; A_Z为转向器进油口通流面积, mm²; P_cf、P_ef、P_LS、P_S分别为优先阀各口压力, MPa; A₁、A₂分别为优先阀LS、R阻尼孔通流面积, mm²; P_L、P_R分别为优先阀阀芯左腔和右腔压力, MPa; w_cf、w_ef分别为CF、EF口面积梯度, mm²; w_Z为转向器进油口面积梯度, mm²; x_cf、x_ef分别为优先阀CF口、EF口开口量, mm; x_Z为转向器进油口开口量, mm; U_cf、U_ef分别为优先阀阀芯位移为0时CF口、EF口开口量, mm; U_Z为转向器阀芯与阀套相对位移为0时进油口开口量, mm; x为优先阀阀芯位移, mm; x₁为转向器阀芯与阀套展开后线位移差, mm; V₁、V₂分别为优先阀左右腔油液体积, mm³; β _e为优先阀有效体积弹性系数, N/mm; A_f为优先阀阀芯作用面积, mm²。

优先阀阀芯力平衡方程如下:

$\begin{matrix} \begin{matrix} P_{L} = P_{LS} - {(\frac{Q_{LS}}{C_{d} A_{1}})}^{2} \frac{ρ}{2} (14) \\ P_{R} = P_{cf} - {(\frac{Q_{R}}{C_{d} A_{2}})}^{2} \frac{ρ}{2} (15) \end{matrix} \end{matrix}$

m_f $\begin{matrix} \overset{\cdot \cdot}{x} \end{matrix}$ =A_f(P_L-P_R)-k(x-x₀)- $\begin{matrix} \overset{\cdot}{cx} \end{matrix}$ (16)

式中:k为优先阀弹簧刚度, N/mm; x₀为优先阀弹簧预压缩量, mm; c为优先阀内部黏性阻尼系数, kg/s; m_f为优先阀阀芯质量, kg。

若把转向器计量马达啮合副理想化(即不考虑摆线副泄漏), 则由转向器的工作原理可知:

$\begin{matrix} \begin{matrix} Q_{Z} = ω_{m} D_{m} / 2 π (17) \\ θ_{m} = 2 π \int_{0}^{t} \frac{Q_{Z}}{D_{m}} dt (18) \\ θ_{f} = \int_{0}^{t} ω_{f} dt (19) \\ θ = θ_{f} - θ_{m} (20) \\ x_{1} = \frac{d}{2} θ = \frac{d}{2} \int_{0}^{t} ω_{f} dt - dπ \int_{0}^{t} \frac{Q_{Z}}{D_{m}} dt (21) \end{matrix} \end{matrix}$

式中:ω _m为计量马达转速, r/min; ω _f为转向器阀芯转速, r/min; θ _m为计量马达角位移, 即阀套角位移, rad; θ _f为转向器阀芯角位移, rad; θ 为转向器阀套与阀芯角位移差, rad; D_m为转向器计量马达排量, L/r; d为转向器阀套与阀芯接合面直径, mm。

优先阀系统的重要输入输出参数图如图3所示。

	Figure Option View Download New Window
	图3 优先阀输入输出关系图Fig.3 Input-output relationship diagram of priority valve

3 优先阀关键参数定性分析

根据转向系统流量连续方程和力平衡方程, 在转向器转速一定的条件下, 得到转向器进油口压差表达式为:

$\begin{matrix} \begin{matrix} Q_{LS} = 0 (22) \\ Q_{R} = 0 (23) \\ P_{L} = P_{LS} (24) \\ P_{R} = P_{cf} (25) \\ ΔP = P_{cf} - P_{LS} = \frac{k (x + x_{0})}{A_{f}} (26) \\ Q_{1} = C_{d} A_{Z} \sqrt{\frac{2 ΔP}{ρ}} (27) \end{matrix} \end{matrix}$

式中:Δ P为转向器进油口压降, MPa。

由于优先阀阀芯位移相对于弹簧预压缩量非常小, 在阀芯运动位移较小条件下, Δ P基本为一个定值, 通过转向器进油口的流量只与转向器进油口面积有关, 即与转向器阀芯转动速度有关, 而与转向负载和工作负载无关^[4]。

对优先阀系统的数学模型式(4)~式(21)进行拉氏变换^[5]:

$\begin{matrix} \begin{matrix} X_{1} (s) = \frac{d}{2 s} ω_{f} (s) - \frac{dπ}{s D_{m}} Q_{Z} (s) (28) \\ Q_{Z} (s) = Q_{1} (s) - Q_{LS} (s) (29) \\ Q_{1} (s) = Q_{cf} (s) - Q_{R} (s) (30) \\ Q_{S} (s) = Q_{ef} (s) + Q_{cf} (s) (31) \\ Q_{cf} (s) = K_{qcf} X (s) + K_{ccf} (P_{S} (s) - P_{cf} (s)) (32) \\ Q_{ef} (s) = - K_{qef} X (s) + K_{cef} (P_{S} (s) - P_{ef} (s)) (33) \\ Q_{1} (s) = K_{q 1} X (s) - K_{c 1} (P_{cf} (s) - P_{LS} (s)) (34) \\ Q_{LS} (s) = K_{cLS} (P_{LS} (s) - P_{L} (s)) (35) \\ Q_{R} (s) = K_{cR} (P_{cf} (s) - P_{R} (s)) (36) \\ Q_{LS} (s) - A_{f} sX (s) = \frac{V_{1}}{β_{e}} s P_{L} (s) (37) \\ A_{f} sX (s) - Q_{R} (s) = \frac{V_{2}}{β_{e}} s P_{R} (s) (38) \\ m_{f} s^{2} X (s) = A_{f} (P'_{L} (s) - P_{R} (s)) - (k + cs) X (s) (39) \end{matrix} \end{matrix}$

式中:K_qcf、K_qef、K_q1分别为CF口、EF口、转向器进油口流量增益; K_ccf、K_cef、K_c1、K_cLS、K_cR分别为CF口、EF口、转向器进油口、LS阻尼孔、R阻尼孔流量-压力系数。

令转向器阀芯转速输入信号ω _f(s)、转向负载输入信号P_LS(s)、工作负载输入信号P_ef(s)为系统的输入信号; 转向器流量输出Q_Z为系统的输出信号, 根据式(28)~式(39)得到系统的传递函数框图如图4所示。

	Figure Option View Download New Window
	图4 系统传递函数框图Fig.4 System transfer function block diagram

由系统的传递函数框图可知, 决定系统响应的参数K_qcf、K_qef、K_q1、K_ccf、K_cef、K_c1、K_cLS、K_cR主要受c_d、ρ 、A₁、A₂、w_cf、w_ef、w_Z等参数的影响, β _e、K、A_f、V₁、V₂同样影响系统的响应。根据优先阀优化方案的可实施性, 将其结构参数A₁、A₂、K、A_f作为关键参数进行仿真分析和优化^{[6, 7]}。

4 仿真模型建立及仿真分析

4.1 模型建立

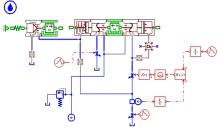
采用AMESim软件提供的液压元件设计库, 面向实际结构对优先阀建模^{[4, 8]}。优先阀仿真模型如图5所示, 参数按照其实际结构设置, 如下所示:阀芯作用面积A_f=25 mm; 主弹簧刚度K=31 N/mm; R阻尼孔直径d₂=1.2 mm; LS阻尼孔直径d₁=1 mm。

	Figure Option View Download New Window
	图5 优先阀仿真模型Fig.5 The HCD model of priority valve

4.2 仿真分析

4.2.1 仿真与实验对比

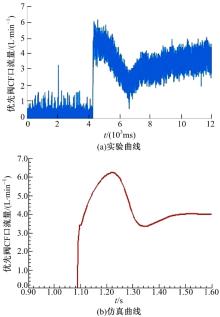
图6(a)(b)分别为优先阀转向流量的实验曲线和仿真曲线, 仿真条件为:Q_S=100 L/min; P_LS=3.9× 10⁵ Pa; P_ef=0.43× 10⁵ Pa。从图6可以看出, 二者的稳态值、超调量等基本吻合, 说明该模型能够反映实际系统工作情况, 在此模型上进行的仿真分析具有实用意义。

	Figure Option View Download New Window
	图6 优先阀CF口流量实验和仿真曲线Fig.6 Experimental and simulation curves of CF port flow

4.2.2 结果分析

优先阀CF口流量响应受系统输入(转向负载、工作负载、转向器转速、优先阀供油流量)和系统本身的参数(优先阀阀芯作用面积A_f、优先阀主弹簧K、优先阀R阻尼孔直径d₁、优先阀LS阻尼孔直径d₂)的影响。

(1)不同输入对流量响应的影响

以阶跃信号模拟恒定方向盘转速, 1 s时转向器转速阶跃至50 r/min, 图7~图9为CF口流量对不同系统输入的响应。

	Figure Option View Download New Window
	图7 不同工作负载对转向流量的响应Fig.7 Response of CF port flow for different workload

	Figure Option View Download New Window
	图8 不同转向负载对转向流量的响应Fig.8 Response of CF port flow for different steering load

	Figure Option View Download New Window
	图9 优先阀CF口流量对不同供油流量的响应Fig.9 Response of CF port flow for different oil flow

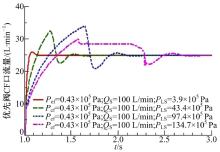
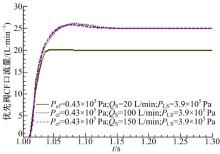
仿真结果表明, 优先阀在恒定的转向器转速条件下输出恒定转向流量。图7表明在一定范围内工作负载的增大与空载时相比转向流量响应上升时间减小, 但存在一定的滞后。图8表明转向负载越大, 转向流量响应越慢; 超调量越大, 稳定性差, 转向负载对于转向流量响应有着不可避免的影响。图9表明在系统供油流量满足转向需求的条件下, 供油流量的大小对转向流量的响应无显著影响。

(2)系统自身参数对流量响应的影响

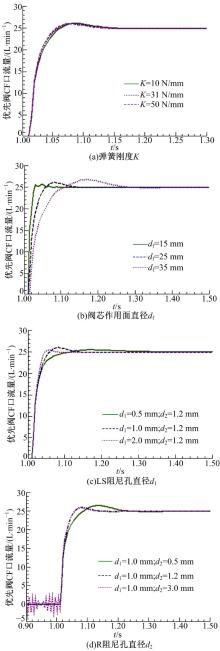
一定方向盘转速下, 改变影响系统的重要参数A_f、K、d₁、d₂观察转向流量响应, 结果如图10(a)(b)(c)(d)所示, 仿真条件同图6。

	Figure Option View Download New Window
	图10 转向流量对不同系统参数的响应Fig.10 Response of CF port flow for different system parameters

图10(a)表明, 优先阀弹簧刚度K对优先阀转向流量动态特性没有显著影响。图10(b)表明, 随着优先阀阀芯作用面积的增大, 优先阀CF流量响应上升时间增大, 调节时间增加, 响应缓慢, 作用面积较小时, 流量响应振荡严重。同时, 阀芯作用面积的增加, 不可避免引起阀芯质量的增大, 影响系统的固有频率。图10(c)和10(d)表明:LS和R阻尼孔太小, 系统的响应速度变慢, 太大又会增大系统的振荡。

(3)参数优化

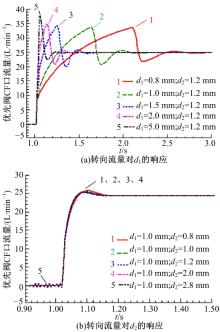
通过分析仿真结果可知, 优先阀LS、R节流孔直径对转向流量响应有着重要的影响, 因此将其作为优化目标。图11(a)为转向流量对不同LS阻尼孔大小d₁的响应, 令P_LS=94.7× 10⁵ Pa; 其他仿真条件同图6; 图11(b)为转向流量对不同R阻尼孔大小d₂的响应, 令P_LS=3.9× 10⁵ Pa; 其他仿真条件同图6。

	Figure Option View Download New Window
	图11 转向流量对d₁和d₂的响应Fig.11 Response of CF port flow for different d₁ and d₂

图11(a)(b)表明, 转向重载条件下, 随着LS阻尼孔的增大, 转向流量响应上升时间减小, 但是当LS阻尼孔直径大于1.5 mm时, 超调量随着孔径的增大而增大, 但是上升时间并无显著变化; 当R阻尼孔大于1 mm, 阻尼孔大小对响应的影响减弱, 随着阻尼孔的增大, 响应基本一致。但当R阻尼孔直径达到2.8 mm时, 系统在不转向时存在轻微振荡。

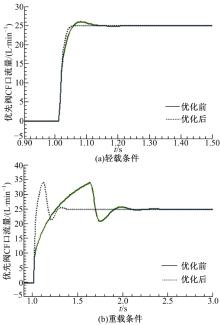
取d₁=2 mm、d₂=2 mm对优先阀CF口流量响应进行优化。图12(a)(b)为转向轻、重载情况下优化前后对比, 其中图12(a)中P_LS=3.9× 10⁵ Pa; 图12(b)中P_LS=97.4× 10⁵ Pa; 其他仿真条件同图6。结果表明, 适当增大LS、R阻尼孔可以提高转向流量响应的灵敏性和稳定性。

	Figure Option View Download New Window
	图12 轻、重载条件下优化前后转向流量响应对比曲线Fig.12 Response of CF port flow before and after optimization under light and heavy load condition

5 结论

(1)建立了负荷传感优先阀数学模型, 针对优先阀转向流量响应, 推导了其控制框图, 定性地分析了优先阀的重要参数对转向系统性能的影响, 并建立了该优先阀的AMESim模型, 通过优先阀台架试验验证了该模型的正确性。

(2)仿真分析了优先阀系统对不同输入的响应, 结果表明转向负载、工作负载和优先阀阀芯作用面积A_f、优先阀R阻尼孔直径d₁、优先阀LS阻尼孔直径d₂均对转向流量动态响应的快速性和稳定性产生一定影响。

(3)根据仿真结果, 适当增大LS和R孔直径, 可以减小转向流量动态响应的超调量和上升时间。该结果为优先阀的设计和转向系统的问题分析提供了可靠的理论支撑。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	尹国会, 赵向阳, 景军清, 等. 负荷传感转向系统[J]. 流体传动与控制, 2005(1): 44-45. Yin Guo-hui, Zhao Xiang-yang, Jing Jun-qing, et al. Load sensing steering hydraulic system[J]. Feuid Power Transmission & Control, 2005(1): 44-45. [本文引用:1]
[2]	侯友山, 石博强, 谷捷. 负荷传感转向液压系统优先阀的稳健设计[J]. 农业工程学报, 2010, 26(10): 129-133. Hou You-shan, Shi Bo-qiang, Gu Jie. Robust design of priority valve in load sensing hydraulic steering system[J]. Transactions of the CSAE, 2010, 26(10): 129-133. [本文引用:1]
[3]	杨忠炯, 何清华. 铰接车辆液压动力转向系统动态特性仿真[J]. 中南大学学报: 自然科学版, 2004, 35(1): 80-85. Yang Zhong-jiong, He Qing-hua. Simulation of dynamic chsracteristics of hydraulic power steering system of articulated vehicles[J]. Journal of Centralsouth University(Natural Science), 2004, 35(1): 80-85. [本文引用:2]
[4]	赵锋. 装载机全液压转向系统机液联合仿真与实验研究[D]. 长春: 吉林大学机械科学与工程学院, 2012. Zhao Feng. Mechanical-hydraulic co-simulation and experimental research on loader full hydraulic steering system [D]. Changchun: School of Mechanical Science and Engineering, Jilin University, 2012. [本文引用:4]
[5]	刘豹. 现代控制理论[M]. 北京: 机械工业出版社, 1998. [本文引用:1]
[6]	弓永军, 王祖温, 徐杰, 等. 先导式纯水溢流阀仿真与试验研究[J]. 机械工程学报, 2010, 46(24): 136-142. Gong Yong-jun, Wang Zu-wen, Xu -jie, et al. Simulation and experiments study on water hydraulic pressure relief valve with pilot stage[J]. Journal of Mechanical Engineering, 2010, 46(24): 136-142. [本文引用:1]
[7]	杜恒, 魏建华, 冯瑞琳. 压力跟踪阀建模、仿真与试验研究[J]. 浙江大学学报: 工学版, 2012, 46(6): 1034-1040, 1047. Du Heng, Wei Jian-hua, Feng Rui-lin. Modeling, simulation and experimental research on pressure tracking valve[J]. Journal of Zhejiang University(Engineering Science), 2012, 46(6): 1034-1040, 1047. [本文引用:1]
[8]	王同建, 陈晋市, 赵锋, 等. 全液压转向系统机液联合仿真及试验[J]. 吉林大学学报: 工学版, 2013, 43(3): 607-612. Wang Tong-jian, Chen Jin-shi, Zhao Feng, et al. Mechanical-hydraulic co-simulation and experiment of full hydraulic steering systems[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(3): 607-612. [本文引用:1]

2005

0.0

. 2005, (1):44-45 DOI:doi:10.3969/j.issn.1672-8904.2005.01.015

Load sensing steering hydraulic system

负荷传感转向系统

Yin Guo-hui , Zhao Xiang-yang , Jing Jun-qing

尹国会, 赵向阳, 景军清

负荷传感转向液压系统能够按照转向油路的要求,优先向其分配流量,无论负载压力大小,方向盘转速高低,均能保证供油充足,因此转向动作平滑可靠.

... 目前,采用铰接式转向的工程机械大都装配负荷传感全液压转向系统^[1],而负荷传感优先阀是负荷传感全液压转向系统的核心元件,其功能结构可等效为A型半桥回路,流量增益较大,阀芯移动较小的位移,转向流量将产生大幅变化,具有良好的动态特性 ...

2010

0.0

. 2010, 26(10):129-133 DOI:doi:10.3969/j.issn.1002-6819.2010.10.021

Robust design of priority valve in load sensing hydraulic steering system

负荷传感转向液压系统优先阀的稳健设计

Hou You-shan , Shi Bo-qiang , Gu Jie.

侯友山, 石博强, 谷捷

The aim of the research is to realize the robust design of priority valve. Based on the analytical method and SIMULINK software, the dynamic mathematical model and simulation model of priority valve were established, and the influence characteristics of system parameters on priority valve dynamic response were analyzed. On basis of analyzing the main influencing factors on dynamic response, the robust design based on loss model was completed, by using the minimum overshoot of priority steering system flow response as the design objective, the valve core diameter, spring stiffness and throttle area as the design variables, the steering wheel angular, steering load, work load and output flow as the uncertain factors. The results show that robust design can improve design objective to a certain extent, the dynamic response characteristic of priority valve is promoted. The design method is also applicable to other valves design improvement.

为了实现优先阀的稳健设计，基于解析法及SIMULINK分别建立了优先阀动态数学模型及仿真模型，仿真分析了系统各参数变化对优先阀动态响应特性的影响规律。在分析动态响应特性主要影响因素的基础上，以优先阀转向系统的流量响应超调量最小为设计目标，以优先阀的阀芯直径、弹簧刚度及节流口面积为设计变量，以方向盘角速度、转向负载、工作负载及输出流量为不确定因素，完成了基于损失模型的稳健设计。结果表明，稳健设计提高了设计目标的稳健性，一定程度上提升了优先阀的动态响应特性，该设计方法同样适用于其他阀件的改进设计。

... 但是以往研究鲜有对优先阀进行完整的数学模型搭建^[2,3],且通常直接简化数学模型运用Simulink等软件仿真^[3] ...

2004

0.0

. 2004, 35(1):80-85 DOI:doi:10.3969/j.issn.1672-7207.2004.01.016

Simulation of dynamic chsracteristics of hydraulic power steering system of articulated vehicles

铰接车辆液压动力转向系统动态特性仿真

Yang Zhong-jiong , He Qing-hua.

杨忠炯, 何清华

摘　要：利用液压控制理论和SIMULINK控制系统仿真软件，以DQ-18型地下运矿卡车(地下汽车)液压动力转向系统为例，计算并仿真铰接车辆液压动力转向系统的动态特性，仿真结果为设计液压动力转向机构提供理论依据。研究结果表明：负载质量决定液压转向系统的响应速度，响应速度与负载质量成反比。为改善液压转向系统的动态特性，应减少转向油缸负载质量，同时缩短转向系统液压管路的长度以减少液压管路中油液质量；液压系统的有效液体体积弹性模数对液压系统的动态响应速度影响很大，严格控制液压系统中空气的含量，同时液压管路采用钢管以及缩短液压胶管的长度，以改善系统的动态特性。该液压动力转向系统仿真模型针对不同的液压转向系统，只需改变个别参数，就可对液压转向系统进行仿真和优化设计。

... 但是以往研究鲜有对优先阀进行完整的数学模型搭建^[2,3],且通常直接简化数学模型运用Simulink等软件仿真^[3] ...

2012

0.0

. 2012, :-

Mechanical-hydraulic co-simulation and experimental research on loader full hydraulic steering system

装载机全液压转向系统机液联合仿真与实验研究[D]

Zhao Feng.

赵锋

装载机是工程机械中广泛使用的机种，在工程建设项目中发挥着重要的作用。转向系统是装载机重要的子系统之一，转向系统的性能好坏直接关系到装载机的安全可靠性，因此对于转向系统的研究工作具有重要的意义。以往对于转向系统的研究大多基于系统的数学模型，对于元件及负载都进行了多种简化和等效，特别是对于转向系统的负载无法建立准确的模型。基于此，本文结合校企合作项目“装载机液压系统及传动系统动态仿真分析及对比测试研究”，以铰接式装载机的负荷传感全液压转向系统为研究对象，采用机液联合仿真的方法对转向系统的动态特性进行了分析研究。本文根据优先阀、转向器的实际结构，详细分析了转向系统两大关键元件的工作原理，通过对优先阀和转向器建立静态数学模型，分析了二者的静态特性；同时，对轮胎进行了相关的理论分析。在此基础上，利用AMESim软件建立了优先阀和转向器的仿真模型，其中对转向器提出一种全新的建模方式，可以充分体现转向器的实际结构并保证其位移控制随动功能，进而很好地反映其原理性能。根据不同工况，对转向系统进行了动态仿真分析，通过仿真发现两个转向油缸的运动有一定区别，其中转向同侧的油缸运动速度稍快，活塞杆位移较大，指出一直以来的误区，为以后的设计工作提供了参考。通过铰接式装载机的转向系统实验，验证了仿真模型的正确性，并分析了系统的动态性能。鉴于一直以来对于转向系统负载等效的困难，本文通过多体动力学仿真软件LMS Virtual.Lab Motion建立了铰接式装载机的动力学仿真模型，充分考虑了转向机构和轮胎与地面作用对转向的影响，并与AMESim进行机液联合仿真，通过与实验的对比证明，联合仿真结果与实验结果比较接近，可以很好地反映实际情况，从而为转向系统的负载模拟开辟了一种新的途径。同时，通过对不同工况的联合仿真，分析了转向过程中轮胎的受力情况及其对系统压力的影响，并发现适当减小轮胎的侧偏刚度有利于减小转向的压力振摆现象，为以后的研究工作提供了参考。

... 因此,通过动态调节使得CF口与LS口压差基本为一个定值,而转向流量与转向器进油口大小成正比,等于转向器转速乘以转向器计量马达排量^[4] ...

... 优先阀各个节流口流量关系如下^[4]: ...

... P基本为一个定值,通过转向器进油口的流量只与转向器进油口面积有关,即与转向器阀芯转动速度有关,而与转向负载和工作负载无关^[4] ...

... 1 模型建立采用AMESim软件提供的液压元件设计库,面向实际结构对优先阀建模^[4,8] ...

1998

0.0

... 对优先阀系统的数学模型式(4)~式(21)进行拉氏变换^[5]: ...

2010

0.0

. 2010, 46(24):136-142 DOI:doi:10.3901/JME.2010.24.136

Simulation and experiments study on water hydraulic pressure relief valve with pilot stage

先导式纯水溢流阀仿真与试验研究

Gong Yong-jun , Wang Zu-wen , Xu -jie

弓永军, 王祖温, 徐杰

针对具有高压引流和二级节流新型结构阀口的先导式纯水溢流阀进行仿真和试验研究,建立阀的AMESim仿真模型,分析先导阀导向间隙、阻尼孔直径、敏感腔体积、阀芯质量以及弹簧刚度等不同参数对先导式纯水溢流阀特性的影响,在纯水液压综合性能试验台上进行先导式纯水溢流阀的静动态试验,并对仿真和试验结果进行对比分析.仿真与试验结果表明,液阻直径是先导式纯水溢流阀最主要的影响参数,而阀芯质量变化的影响则基本可以忽略;在小于20 L/min的小流量工况下的定压精度较低,而大于20 L/min的大流量工况下的定压精度较高;阀的动态响应试验表明,入口压力超调量小于30%,并且压力上升时间小于80 ms.

... 根据优先阀优化方案的可实施性,将其结构参数A₁、A₂、K、A_f作为关键参数进行仿真分析和优化^[6,7] ...

2012

0.0

. 2012, 46(6):1034-1040,1047 DOI:doi:doi:10.3785/j.issn.1008-973X.2012.06.012

Modeling, simulation and experimental research on pressure tracking valve

压力跟踪阀建模、仿真与试验研究

Du Heng , Wei Jian-hua , Feng Rui-lin.

杜恒, 魏建华, 冯瑞琳

Large engineering equipment with damping system often needs to achieve that the pressure in the elastic element tracks the pressure in the actuator, which can make the system switch smoothly when the elastic element and the actuator are connected. In order to achieve this goal easily, safely and reliably, a pressure tacking valve was designed, and the corresponding mathematical model and the simulation model based on AMESim were established. The feedback link on the valve was analyzed, and the dynamic and static characteristics of the valve under the influences of the spool area, valve opening and damper damping were studied. When the spool diameter is 16 mm, the orifice diameter is 1 mm and the valve opening is zero, the pressure tracking valve has good static and dynamic characteristics of pressure tracking. The test bench was set up and the experimental research was performed. The results show that the pressure tracking error can be controlled in about 0.1 MPa and the stability of the valve is good. The elastic element and the actuator can switch smoothly in the system with the application of the pressure tracking valve.

在应用减振技术的大型液压装备中常常需要实现弹性元件内压力对执行器内压力的跟踪,以保证弹性元件与执行器接通时系统的平稳.为了简易、安全并可靠的实现这一功能,设计了一种压力跟踪阀,建立相应的数学模型及AMESim仿真模型.对阀的反馈环节进行分析并考察阀芯作用面积、阀口开度和阻尼器阻尼对阀动、静态特性的影响.当阀芯直径为16 mm、阻尼孔直径为1 mm且为零开口阀时,压力跟踪阀具有较好的动、静态特性.搭建相关试验台进行试验验证,结果表明：压力跟踪阀可以较好地实现压力跟踪功能,压力跟踪误差可控制在0.1 MPa左右且压力跟踪稳定.应用了压力跟踪阀的系统可以有效的实现弹性元件与执行器之间的平稳切换.

... 根据优先阀优化方案的可实施性,将其结构参数A₁、A₂、K、A_f作为关键参数进行仿真分析和优化^[6,7] ...

2013

0.0

. 2013, 43(3):607-612 DOI:doi:10.7964/jdxbgxb201303009

Mechanical-hydraulic co-simulation and experiment of full hydraulic steering systems

全液压转向系统机液联合仿真及试验

Wang Tong-jian , Chen Jin-shi , Zhao Feng

王同建, 陈晋市, 赵锋

The working principle the load-sensing full hydraulic system was introduced in this paper. The co-simulation model of the hydraulic steering system of a loader was established based on AMESim and LMS Virtual.Lab Motion. The dynamic characteristics of the steering process was simulated and analyzed. Comparison of simulation and experiment results shows that the co-simulation model is accurate and credible. The multi-body dynamic model can accurately simulate the system load. It is found by simulation analysis that tire cornering stiffness significantly affects the pressure oscillation of the steering system, thus reducing the stiffness can reduce the pressure fluctuation.

介绍了负荷传感全液压转向系统工作原理,基于AMESim和LMS Virtual.Lab Motion软件建立了装载机全液压转向系统的联合仿真模型,并对转向系统转向过程的动态特性进行了仿真分析.仿真及试验结果表明:联合仿真模型准确可信,装载机转向多体动力学模型能够准确地模拟系统负载.通过仿真分析发现:轮胎侧偏刚度对转向系统压力振摆具有很大的影响,适当减小该值可以减小压力波动.

... 1 模型建立采用AMESim软件提供的液压元件设计库,面向实际结构对优先阀建模^[4,8] ...