双定子单作用液压马达转子径向受力特性

引用本文

闻德生, 刘巧燕, 刘忠迅, 高俊峰, 周瑞彬. 双定子单作用液压马达转子径向受力特性. 2015, 45(6): 1825-1830
WEN De-sheng, LIU Qiao-yan, LIU Zhong-xun, GAO Jun-feng, ZHOU Rui-bin. Rotor radial force of double-stator single-acting motor. Journal of Jilin University Engineering and Technology Edition, 2015, 45(6): 1825-1830 复制到剪切板

Permissions

双定子单作用液压马达转子径向受力特性

闻德生, 刘巧燕, 刘忠迅, 高俊峰, 周瑞彬

燕山大学机械工程学院,河北秦皇岛 066004

作者简介:闻德生(1954-),男,教授,博士生导师.研究方向:新型液压元件及新型液压传动.E-mail:wendesheng@ysu.edu.cn

基金:国家自然科学基金项目(50975246)

摘要

双定子单作用液压马达有内外马达分别单独工作、内外马达联合工作、内外马达差动工作4种工况,分析了不同工况下转子的受力状况及奇、偶叶片数对转子受力的影响,推导出了各工况下转子受力的表达式,同时根据液压马达样机参数采用MATLAB对转子受力情况进行了仿真。结果表明:转子在4种不同受力状态下所受径向力都在一定范围内做周期性的变化,与传统叶片马达相比,双定子马达转子径向受力较好,且奇数叶片时的转子受力状态更好,为双定子单作用液压马达变量机构的设计奠定了理论基础。

关键词: 流体传动与控制; 双定子单作用马达; 差动连接; 受力特性

中图分类号:TH32 文献标志码:A 文章编号:1671-5497(2015)06-1825-06

Rotor radial force of double-stator single-acting motor

WEN De-sheng, LIU Qiao-yan, LIU Zhong-xun, GAO Jun-feng, ZHOU Rui-bin

School of Mechanical Engineering, Yanshan University, Qinhuangdao 066004,China

Abstract

Single-acting double-stator motor has four operating states, including inner or outer motor working alone, inner and outer motor united working and differential operating states. Through the calculation of the hydraulic force acting on the rotor in different operating states, the formula of acting force is acquired, the effect of the vane number, which is odd or even, on the acting force is considered. The simulation according to the prototype was carried out using MATLAB. The results show that the rotor radial force varies periodically within a certain range under four strained conditions. Compared with that of the classical vane pumps, the strained conditions of the rotor of single-acting double-stator are better. This study may provide reference for the design of the variable displacement mechanism for single-acting double-stator hydraulic motors.

Keyword: fluid transmission and control; double-stator single-acting multi-motor; differential connection; mechanical characteristic

Show Figures

液压传动所具有的独特优越性, 使它的应用非常广泛^[1]。液压泵和液压马达的性能和寿命在很大程度上决定着整个液压系统的工作能力^[2]。当前, 国内外研究人员大多是在现有液压泵或马达原理的基础上, 致力于提高元件性能, 改善各部件的材料、润滑条件, 提高元件寿命^{[3, 4, 5, 6]}。对泵和马达的工作原理进行深入研究的人员却很少。

双定子单作用液压马达由一个转子对应两个定子, 且有等宽的内外定子曲线, 故其有无需回程装置、叶片不脱空、比功率大、能差动工作等优点^{[7, 8, 9, 10, 11, 12, 13, 14]}。目前已获国家发明专利^[15], 属原创技术, 是在原理和结构上的突破, 该双定子马达完成后可取代一系列中低压马达, 广泛应用于汽车、船舶等领域。

转子受到的径向力不平衡使得单作用液压马达的工作压力和使用寿命受到限制。因此, 对双定子液压马达的转子进行径向受力分析在理论和工程上都具有重要的意义。本文采用理论分析与仿真相结合的方法, 对双定子液压马达在4种工况下转子的径向受力规律进行了研究, 为今后的研究工作奠定了理论基础。

1 双定子单作用液压马达工作原理

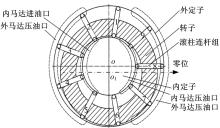
双定子单作用连杆滚柱式液压马达是双定子单作用液压马达中的一种, 图1为该马达的工作原理图, 马达结构如图2所示。其中, 由外定子、转子、滚柱连杆组和两边侧板形成外马达的变化容腔; 同理, 由内定子、转子、滚柱连杆组和两边侧板形成内马达的变化容腔。

	Figure Option View Download New Window
	图1 双定子液压马达原理简图Fig.1 Operating principle of double-stator motor

	Figure Option View Download New Window
	图2 双定子单作用液压马达的结构Fig.2 Structure of double-stator single-acting motor

连杆滚柱型双定子马达的主要结构特点为:

(1)滚柱与外定子的内表面和内定子的外表面为滚动摩擦, 液压马达的摩擦副之间均有润滑, 提高了马达的机械效率, 延长了其使用寿命。

(2)马达的外定子环的内表面和内定子环的外表面为相似的等距曲面, 叶片为连杆滚柱结构, 因此不需要压紧机构或回程弹簧。

(3)连杆的半圆槽半径略大于滚柱的半径, 可使得滚柱磨损后能够自动补偿, 从而减小液压马达的径向泄漏。

2 内、外马达单独工作时转子的径向力分析

单作用双定子马达转子受到的径向力是由直接作用在转子圆周上的液压力和作用在封油区滚柱连杆组上的液压力组成。分析可知双定子单作用连杆滚柱马达的外马达单独工作时转子的径向力F_外为:

$\begin{matrix} \begin{matrix} F_{外} = \sqrt{{(F_{x 外} + P_{x 外})}^{2} + {(F_{y 外} + P_{y 外})}^{2}} \\ (1) \end{matrix} \end{matrix}$

方向为:α _外=arctan $\begin{matrix} \frac{F_{y 外} + P_{y 外}}{F_{x 外} + P_{x 外}} \end{matrix}$ 。

式中:F_x_外、F_y_外分别为转子在x、y方向上的液压合力:

$\begin{matrix} \{\begin{matrix} F_{x 外} = \overset{(z + 1) N / (2 z)}{\sum_{n = 1}} - p_{0} BR φ_{0} \cos [φ + (n - 1) φ_{0}] + \\ \overset{N}{\sum_{(z + 1) N / (2 z)}} - p_{1} BR φ_{0} \cos [φ + (n - 1) φ_{0}] \\ F_{y 外} = \overset{(z + 1) N / (2 z)}{\sum_{n = 1}} - p_{0} BR φ_{0} \sin [φ + (n - 1) φ_{0}] + \\ \overset{N}{\sum_{(z + 1) N / (2 z)}} - p_{1} BR φ_{0} \sin [φ + (n - 1) φ_{0}] \end{matrix} (2) \end{matrix}$

φ 为滚柱连杆组随转子转过的角度; P_x_外、P_y_外分别为封油区滚柱连杆受的液压力在x、y方向上的合力:

$\begin{matrix} \begin{matrix} \{\begin{matrix} P_{x 外} = P_{1} sinφ + P_{2} \sin [\frac{z + 1}{2} \cdot \frac{2 π}{z} + φ] \\ P_{y 外} = P_{1} cosφ + P_{2} \cos [\frac{z + 1}{2} \cdot \frac{2 π}{z} + φ] \end{matrix} \\ (3) \end{matrix} \end{matrix}$

N为以滚柱连杆1为起点(如图1所示)将转子外圆周等分的压力分布区个数; n为按逆时针方向依次规定的第1, 第2, …, 第n个压力分布区序号; P₁、P₂分别为处于封油区的滚柱连杆所受的液压力; z为滚柱连杆数; R为转子外径; φ ₀=2π /N。

同理, 内马达单独工作时转子的径向力F_内以及方向α _内也可得出, 只需将转子外径R替换为转子内径r即可, 不再赘述。

3 内、外马达联合工作时转子的径向力分析

双定子单作用液压马达能实现内外马达联合工作以及差动工作, 即可进行4种定转速和定转矩的切换。因此, 对内外马达联合工作以及差动连接下转子的径向力分析尤为重要。

3.1 转子圆周上径向液压力的计算

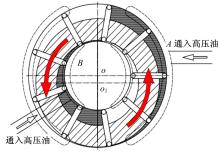
以滚柱连杆1为起点将转子圆周等分为N个压力分布区, 按逆时针方向依次规定为第1, 第2, …, 第n个压力分布区。图3为内外马达联合工作时的通油方式, 即向进油口A、B同时通油, 当外马达的压力分布区处于高压油作用时, 内马达的压力分布区位于低压油作用, 从而使转子受到外马达指向圆心的径向液压力和内马达背离圆心的径向液压力。因此, 可得出内外马达联合工作时转子圆周上第n压力分布区的总径向液压力为:

$\begin{matrix} F_{n} = \{\begin{matrix} B φ_{0} (R p_{0} - r p_{1}), 1 \leq n \leq \frac{z + 1}{2 z} N \\ B φ_{0} (R p_{1} - r p_{0}), \frac{z + 1}{2 z} N < n \leq N \end{matrix} (4) \end{matrix}$

则可得转子在x、y方向上的液压合力为:

$\begin{matrix} \{\begin{matrix} F_{x 1} = \overset{(z + 1) N / (2 z)}{\sum_{n = 1}} - B φ_{0} (R p_{0} - r p_{1}) \\ \cos [φ + (n - 1) φ_{0}] + \overset{N}{\sum_{(z + 1) N / (2 z)}} - B φ_{0} \\ (R p_{1} - r p_{0}) \cos [φ + (n - 1) φ_{0}] \\ F_{y 1} = \overset{(z + 1) N / (2 z)}{\sum_{n = 1}} - B φ_{0} (R p_{0} - r p_{1}) \\ \sin [φ + (n - 1) φ_{0}] + \overset{N}{\sum_{(z + 1) N / (2 z)}} - B φ_{0} \\ (R p_{1} - r p_{0}) \sin [φ + (n - 1) φ_{0}] \end{matrix} (5) \end{matrix}$

	Figure Option View Download New Window
	图3 内外马达联合工作时的通油方式Fig.3 Inner and outer motor unite working operating condition

3.2 封油区滚柱连杆上液压力的计算

内外马达联合工作时处于封油区的连杆受力简图如图4所示, 作用在滚柱连杆向外马达处悬伸部分的液压力方向与作用在向内马达处悬伸部分的液压力方向相反。因此, 内外马达联合工作时作用于封油区滚柱连杆上总的液压力为:

$\begin{matrix} P = B (p_{1} - p_{0}) (l_{1} - l_{2}) (6) \end{matrix}$

	Figure Option View Download New Window
	图4 内外马达联合工作时封油区连杆受力简图Fig.4 Rod’ s force diagram in seal oil region when inner and outer motor unite working

式中:l₁、l₂分别为滚柱连杆在外马达中悬伸的长度和在内马达中悬伸的长度, 表达式为:

$\begin{matrix} \{\begin{matrix} l_{1} = \sqrt{R_{1}^{2} - e^{2} co s^{2} φ} + esinφ - R \\ l_{2} = r - [\sqrt{R_{2}^{2} - e^{2} co s^{2} φ} + esinφ] \end{matrix} (7) \end{matrix}$

式中:R₁为外定子半径, mm; R₂为内定子半径, mm; e为偏心距, mm。

则在封油区的两个滚柱连杆在x、y方向上的分力为:

$\begin{matrix} \{\begin{matrix} P_{1 x} = P_{1} sinφ \\ P_{1 y} = P_{1} cosφ \\ P_{2 x} = P_{2} \sin (\frac{z + 1}{2} \cdot \frac{2 π}{z} + φ) \\ P_{2 y} = P_{2} \cos (\frac{z + 1}{2} \cdot \frac{2 π}{z} + φ) \end{matrix} (8) \end{matrix}$

在x、y方向上的合力为:

$\begin{matrix} \{\begin{matrix} P_{x} = P_{1 x} + P_{2 x} \\ P_{y} = P_{1 y} + P_{2 y} \end{matrix} (9) \end{matrix}$

由以上分析可得出转子所受径向合力为:

$\begin{matrix} \begin{matrix} F_{1} = \sqrt{{(F_{x 1} + P_{1 x})}^{2} + {(F_{y 1} + P_{1 y})}^{2}} \\ (10) \end{matrix} \end{matrix}$

其方向为α ₁=arctan $\begin{matrix} \frac{F_{y 1} + P_{1 y}}{F_{x 1} + P_{1 x}} \end{matrix}$ 。

4 内外马达差动连接时转子的径向力分析

4.1 转子圆周上径向液压力的计算

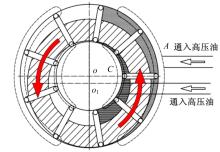
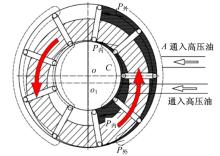
内外马达差动连接时的通油方式如图5所示, 当内外马达差动连接时, 外马达和内马达的压力分布区同时受到高压油的作用力或同时受到低压油的作用力。这样使得转子也同时受到外马达指向圆心的径向液压力和内马达背离圆心的液压力。因此, 可得出内外马达差动连接时转子圆周上第n个压力分布区的总径向液压力为:

$\begin{matrix} F_{n} = \{\begin{matrix} B p_{0} φ_{0} (R - r), 1 \leq n \leq \frac{z + 1}{2 z} N \\ B p_{1} φ_{0} (R - r), \frac{z + 1}{2 z} N < n \leq N \end{matrix} (11) \end{matrix}$

	Figure Option View Download New Window
	图5 内外马达差动连接时的通油方式Fig.5 Inner and outer motor unite working differential operating condition

则可得转子在x、y方向上的液压合力为:

$\begin{matrix} \{\begin{matrix} F_{x 2} = \\ \overset{(z + 1) N / (2 z)}{\sum_{n = 1}} - B p_{0} φ_{0} (R - r) \cos [φ + (n - 1) φ_{0}] + \\ \overset{N}{\sum_{(z + 1) N / (2 z)}} - B p_{1} φ_{0} (R - r) \cos [φ + (n - 1) φ_{0}] \\ F_{y 2} = \\ \overset{(z + 1) N / (2 z)}{\sum_{n = 1}} - B p_{0} φ_{0} (R - r) \sin [φ + (n - 1) φ_{0}] + \\ \overset{N}{\sum_{(z + 1) N / (2 z)}} - B p_{1} φ_{0} (R - r) \sin [φ + (n - 1) φ_{0}] \end{matrix} (12) \end{matrix}$

4.2 封油区滚柱连杆上液压力的计算

内外马达差动连接时处于封油区的连杆受力简图如图6所示。当内外马达差动连接时作用在滚柱连杆向外马达处悬伸部分的液压力方向与作用在向内马达处悬伸部分的液压力方向一致。因此, 内外马达差动连接时作用于封油区滚柱连杆上总的液压力为:

$\begin{matrix} P' = B (p_{1} - p_{0}) (l_{1} + l_{2}) (13) \end{matrix}$

内外马达差动连接时在封油区的两个滚柱连杆在x、y方向上的分力与内外马达联合工作时类似, 只需将P'替换P即可。

	Figure Option View Download New Window
	图6 内外马达差动连接时封油区连杆受力简图Fig.6 Rod’ s force diagram in seal oil region when Inner and outer motor unite working differential operating condition

则内外马达差动连接时转子的径向合力为:

$\begin{matrix} \begin{matrix} F_{2} = \sqrt{{(F_{x 2} + P'_{1 x})}^{2} + {(F_{y 2} + P'_{1 y})}^{2}} \\ (14) \end{matrix} \end{matrix}$

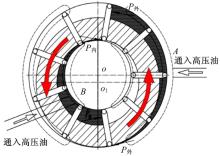
其方向为:α ₂=arctan $\begin{matrix} \frac{F_{y 2} + P'_{2 y}}{F_{x 2} + P'_{2 x}} \end{matrix}$ 。

5 双定子单作用液压马达径向受力仿真分析

根据双定子单作用液压马达的特点, 可通过调节电磁换向阀的通断, 实现液压马达各种连接方式之间的自由切换, 输出不同的转矩和转速。马达的连接方式如图7所示。

	Figure Option View Download New Window
	图7 双定子单作用液压马达连接方式Fig.7 Connection of single-acting double-stator motor

为了更直观地分析双定子液压马达各种工况下转子的受力情况及规律, 根据双定子单作用液压马达样机参数, 并参考文献[8], 对奇数叶片9与偶数叶片8的双定子马达, 使用MATLAB软件分别对其转子的径向受力及方向在一个周期内进行分析和计算^[16]。样机各项参数设置如下:额定压力为6.3 MPa; 转速为150~2000 r/min; 排量为35 ml/r; 内、外定子直径分别为80、140 mm; 转子内、外径分别为90、128 mm; 转子宽为45 mm。

以图1所示的零位位置以及滚柱连杆1所在位置为起始角度对滚柱连杆1转到2时进行分析, 结果如表1和表2所示。

表1 滚柱连杆组数取8时转子径向合力F及方向α Table 1 Rotor’ s radial force F and direction α when the roller linkage is eight

表2 滚柱连杆组数取9时转子径向合力F及方向α Table 2 Rotor’ s radial force F and direction α when the roller linkage is nine

通过分析表1和表2中数据可知, 当外马达单独工作和内外马达联合工作的工况下, 随着转子的旋转, 马达的径向合力呈逐渐增大的趋势, 而当内外马达差动连接工作时的径向合力是逐渐减小的; 内外马达差动工作工况下转子所受径向力由于内马达油液压力的作用, 远小于内、外马达分别单独工作和联合工作工况。不论外马达单独工作, 内外马达联合工作或是差动连接工作, 转子所受径向力都以T=2π /(zω )的周期进行变化, 且滚柱连杆组为奇数时转子的受力状况要比偶数时好。

6 结论

(1)在双定子液压马达在随着转子旋转的一个作用周期内, 内外马达联合工作时转子的径向合力逐渐增大, 差动连接工作时转子的径向合力逐渐减小。

(2)双定子液压马达在内外马达差动连接工作时转子的径向合力要远小于外马达单独(即传统的单马达)工作与内外马达联合工作时转子的径向合力。

(3)双定子单作用液压马达当叶片数为奇数时转子所受径向合力比偶数时要好, 且马达在不同工况下转子的径向合力的大小及作用位置都以T=2π /(zω )周期进行变化。

(4)双定子单作用液压马达转子受力变化范围与表达式表明该马达的调压弹簧结构应能适应不同工况下转子受力的变化, 为变量机构的设计奠定了理论基础。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	李壮云. 液压元件与系统[M]. 3版. 北京: 机械工业出版, 2011. [本文引用:1]
[2]	黎克英, 陆祥生. 叶片式液压泵和马达[M]. 北京: 机械工业出版社, 1993. [本文引用:1]
[3]	王益群, 张伟. 流体传动及控制技术的评述[J]. 机械工程学报, 2003, 39(10): 95-99. Wang Yi-qun, Zhang Wei. Summary of fluid power transmission and control technology[J]. Chinese Journal of Mechanical Engineering, 2003, 39(10) : 95-99. [本文引用:1]
[4]	柯明纯, 丁凡, 李宾. 背压对液压马达效率影响的探讨[J]. 农业机械学报, 2006, 37(10): 128-131. Ke Ming-chun, Ding fan, Li Bin. Exploration of the influence of backing pressure on the efficiency of hydraulic motor[J]. Transactions of the Chinese Society for Agricultural Machinery, 2006, 37(10) : 128-131. [本文引用:1]
[5]	陈卓如. 低速大扭矩液压马达理论、计算与设计[M]. 北京: 机械工业出版社, 1989. [本文引用:1]
[6]	Bergada J M. A complete analysis of axial piston pump leakage and output flow ripples[J]. Applied Mathematical Modeling, 2012, 36(4): 1731-1751. [本文引用:1]
[7]	Wen De-sheng, Wang Zhi-li, Lv Shi-jun, et al. Single-acting double-stator multi-pumps and multi-motors[J]. Journal of Chongqing University (English Edition), 2010, 9(4): 208-215. [本文引用:1]
[8]	闻德生, 常雪, 张少波, 等. 双定子单作用液压马达转矩脉动研究[J]. 农业机械学报, 2013, 44(2): 238-242. Wen De-sheng, Chang Xue, Zhang Shao-bo, et al. Double stators and other single-acting hydraulic motor torque ripple study[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(2): 238-242. [本文引用:1]
[9]	Wen De-sheng. Theoretical analysis of output speed of multi-pump and multi-motor driving system[J]. Science China: Technology Sciences, 2011, 54(4): 992-997. [本文引用:1]
[10]	Wen De-sheng, Wang Zhi-li, Zhang Yong, et al. Output speed and flow of double-acting double-stator multi-pumps and multi-motors[J]. Journal of Zhejiang University: Science A Applied Physics & Engineering, 2011, 12(4): 301-309. [本文引用:1]
[11]	闻德生, 吕世君, 刘晓晨, 等. 等宽双定子泵和马达的原理研究[J]. 哈尔滨工业大学学报, 2008, 40(11): 1840-1844. Wen De-sheng, Lv Shi-jun, Liu Xiao-chen, et al. Theoretic research on variable displacement of equal width double-stators pump and motor[J]. Journal of Harbin Institute of Technology, 2008, 40(11): 1840-1844. [本文引用:1]
[12]	闻德生. 液压元件的创新与发展[M]. 北京: 航空工业出版社, 2009. [本文引用:1]
[13]	闻德生, 徐添, 杜孝杰, 等. 多泵/多马达容积调速回路的理论分析[J]. 上海交通大学学报, 2011, 45(9): 1294-1298, 1303. Wen De-sheng, Xu Tian, Du Xiao-jie, et al. Multiple pump/volume multi-motor speed control circuit theory analysis[J]. Journal of Shanghai Jiaotong University, 2011, 45(9): 1294-1298, 1303. [本文引用:1]
[14]	闻德生, 郑珍泉, 王远, 等. 非对称型多速液压马达的差动连接转矩转速分析[J]. 吉林大学学报: 工学版, 2014, 44(5): 1342-1346. Wen De-sheng, Zheng Zhen-quan, Wang Yuan, et al. Analysis of rotational speed and torque of differential connection of asymmetric multi-speed hydraulic motor[J] Journal of Jilin University (Engineering and Technology Edition), 2014, 44(5): 1342-1346. [本文引用:1]
[15]	闻德生. 等宽曲线双定子滚柱泵[P]. 中国: 02144406, 2003-03-19. [本文引用:1]
[16]	张铮, 杨文平, 石博强, 等. MATLAB程序设计与实例应用[M]. 北京: 中国铁道出版社, 2003. [本文引用:1]

2011

0.0

... 液压传动所具有的独特优越性,使它的应用非常广泛^[1] ...

1993

0.0

... 液压泵和液压马达的性能和寿命在很大程度上决定着整个液压系统的工作能力^[2] ...

2003

0.0

. 2003, 39(10):95-99 DOI:doi:10.3321/j.issn:0577-6686.2003.10.016

Summary of fluid power transmission and control technology

流体传动及控制技术的评述

Wang Yi-qun , Zhang Wei.

王益群, 张伟

在回顾流体传动及控制技术发展历史的基础上,对20世纪90年代后期以来液压技术的发展作了综合评述,它集众多学科于一体,具有显著的机电液一体化特征,尤其是与计算机技术相结合,使得液压技术在系统设计、控制、故障诊断、虚拟现实等方面有了长足的进步.最后对流体传动及控制技术的发展前景进行了预测,指出关注环保性能;元件与系统的集成化、模块化、智能化、网络化; 新材料的使用将是未来的发展方向.

... 当前,国内外研究人员大多是在现有液压泵或马达原理的基础上,致力于提高元件性能,改善各部件的材料、润滑条件,提高元件寿命^[3,4,5,6] ...

2006

0.0

. 2006, 37(10):128-131 DOI:doi:10.3969/j.issn.1000-1298.2006.10.034

Ding fan, Li Bin. Exploration of the influence of backing pressure on the efficiency of hydraulic motor

背压对液压马达效率影响的探讨

Ke Ming-chun

柯明纯, 丁凡, 李宾

以斜轴式轴向柱塞液压马达为例,建立液压马达效率的数学模型,分析背压对其效率的影响,通过仿真计算和效率测试,得到定负载和定转速下不同背压时的液压马达效率.结果表明,背压的存在,使摩擦转矩增大,液压马达机械效率降低,特别是低负载工况下效率降低更为严重;背压对容积效率影响较小.

... 当前,国内外研究人员大多是在现有液压泵或马达原理的基础上,致力于提高元件性能,改善各部件的材料、润滑条件,提高元件寿命^[3,4,5,6] ...

1989

0.0

... 当前,国内外研究人员大多是在现有液压泵或马达原理的基础上,致力于提高元件性能,改善各部件的材料、润滑条件,提高元件寿命^[3,4,5,6] ...

2012

0.0

... 当前,国内外研究人员大多是在现有液压泵或马达原理的基础上,致力于提高元件性能,改善各部件的材料、润滑条件,提高元件寿命^[3,4,5,6] ...

2010

0.0

... 双定子单作用液压马达由一个转子对应两个定子,且有等宽的内外定子曲线,故其有无需回程装置、叶片不脱空、比功率大、能差动工作等优点^{[7,8,9,10,11,12,13,14]} ...

2013

0.0

. 2013, 44(2):238-242 DOI:doi:10.6041/j.issn.1000-1298.2013.02.043

Double stators and other single-acting hydraulic motor torque ripple study

双定子单作用液压马达转矩脉动研究

Wen De-sheng , Chang Xue , Zhang Shao-bo

闻德生, 常雪, 张少波

In order to realize the performance of motor, the influence of torque pulsation by different number of slider was studied based on the analysis of the theoretical displacement and theoretical torque of double-stator single-acting multi-motors. Through the analysis, mathematical expressions of the motors torque and the number of sliders were obtained. Meanwhile, the results show that lag angle could influence torque pulsation when outer motor and inner motor work at the same time and differential connections. This research work laid a theoretical foundation for the design of double-stator single-acting multi-motors. 

为了解双定子单作用液压马达的性能，在探讨双定子单作用液压马达理论排量和理论转矩的基础上，分析了不同滑块数对液压马达转矩脉动的影响，得出液压马达滑块数与转矩脉动的数学关系式。结果表明，滑块个数为奇数的液压马达的转矩脉动小，进一步推导出滞后角对液压马达差动连接和内、外马达同时工作时的转矩脉动影响。

2011

0.0

2011

0.0

2008

0.0

. 2008, 40(11):1840-1844

Theoretic research on variable displacement of equal width double-stators pump and motor

等宽双定子泵和马达的原理研究

Wen De-sheng , Lv Shi-jun , Liu Xiao-chen

闻德生, 吕世君, 刘晓晨

研究了一种新型双定子泵,该泵由滚柱、两个定子和一个转子组成,可制成单作用、双作用及多作用的双定子泵,实现了一个泵有多个等比例不同流量的输出,且输出的压力间互不影响,对该泵的运动学及试验进行了论述.研究结果表明:该研究能够很好地解决液压系统中的一个泵不用减压阀无法驱动两个以上不同压力系统,一个泵不能控制多缸不同压力、不同流量同步等问题.

2009

0.0

2011

0.0

. 2011, 45(9):1294-1298,1303

Multiple pump/volume multi-motor speed control circuit theory analysis

多泵/多马达容积调速回路的理论分析

Wen De-sheng , Xu Tian , Du Xiao-jie

闻德生, 徐添, 杜孝杰

This paper analyzed the traditional circuit of variable displacement pump or fixed displacement motor. On this basis, a new volume speed circuit which consists of multi-pump or multimotor was proposed. The paper also separately analyzed the operating principle and character of variable displacement pump or fixed displacement multi-motor and variable displacement multi-pump or fixed displacement multi-motor; the character curves were obtained. Compared with the traditional circuit of variable displacement pump or fixed displacement motor it is found that the new volume speed circuit can acquire multi-stage constant torque or multi-stage constant power regulation, which expands the range of speed.

分析了传统单泵/单马达容积调速回路、单泵/多马达回路以及多泵/多马达回路的原理和特性，提出了由多泵、多马达组成的新型容积调速回路，并与单泵/单马达回路进行比较.结果表明，所提出的多泵/多马达回路可以实现多级恒转矩或多级恒功率的调节，扩大了回路的转速和转矩的调节范围.

2014

0.0

. 2014, 44(5):1342-1346 DOI:doi:doi:10.13229/j.cnki.jdxbgxb201405019

Analysis of rotational speed and torque of differential connection of asymmetric multi-speed hydraulic motor

非对称型多速液压马达的差动连接转矩转速分析

Wen De-sheng , Zheng Zhen-quan , Wang Yuan

闻德生, 郑珍泉, 王远

The structure of the asymmetric multi-speed hydraulic motor is analyzed. Then a differential connection method of this type of motor is proposed. The output rotational speed and output torque formulae of the hydraulic motor with different differential connections are obtained through differential connection of the 2 inner 3 outer motor. The general formulae of the output torque and rotational speed are derived about differential connection of this type of motor. At the same time, in order to avoid the failure point and the repeated phenomenon, the effect of the motor factor selection on the differential connection is analyzed. The results show that there more ways of differential connection of asymmetric multi-speed hydraulic motor than that of the ordinary hydraulic motor and it is limited by the motor factor. This study may establish the theoretical foundation for further research of differential connection of this new type of hydraulic motor.

在对非对称型多速液压马达的结构分析的基础上,对该类型马达进行差动连接。通过对内2外3多速马达的差动连接,得出在不同差动连接下液压马达的输出转速和输出转矩的公式,并由此推导出这一类型马达差动连接时转矩转速输出的一般公式。同时分析了马达系数的选取对差动连接的影响,以避免死点和重复现象的出现。得出非对称型多速液压马达相比普通的液压马达有更多方式的差动连接,且受到马达系数的限制。为进一步研究该新型液压马达的差动连接奠定了理论基础。

0.0

... 目前已获国家发明专利^[15],属原创技术,是在原理和结构上的突破,该双定子马达完成后可取代一系列中低压马达,广泛应用于汽车、船舶等领域 ...

2003

0.0

... 为了更直观地分析双定子液压马达各种工况下转子的受力情况及规律,根据双定子单作用液压马达样机参数,并参考文献[8],对奇数叶片9与偶数叶片8的双定子马达,使用MATLAB软件分别对其转子的径向受力及方向在一个周期内进行分析和计算^[16] ...