月基二维转台轴承预紧力和系统刚度计算

引用本文

王智. 月基二维转台轴承预紧力和系统刚度计算. 2015, 45(6): 1831-1835
WANG Zhi. Computation of the relationship between bearing preload of lunar-based two-dimensional turntable and system stiffness. Journal of Jilin University Engineering and Technology Edition, 2015, 45(6): 1831-1835 复制到剪切板

Permissions

月基二维转台轴承预紧力和系统刚度计算

王智

中国科学院长春光学精密机械与物理研究所,长春 130033

作者简介:王智(1978-),男,研究员,博士.研究方向:航天光学遥感器研制.E-mail:wz070611@126.com

基金:国家自然科学基金项目(61108066)

摘要

为了研究在转台结构形式确定的情况下,轴承预紧力与系统刚度的关系,分析了轴承预紧力、轴承刚度和轴系刚度之间的关系,推导了轴承预紧力与轴系固有频率之间的计算公式,并通过有限元分析的方法获得了轴承预紧力与系统固有频率的关系曲线。通过对二维转台固有频率的测试,验证了该方法的正确性,同时为轴承最佳预紧力的确定提供了一个有效的方法。

关键词: 机械设计; 极紫外相机; 二维转台; 轴承; 预紧力; 刚度

中图分类号:TH133.3 文献标志码:A 文章编号:1671-5497(2015)06-1831-05

Computation of the relationship between bearing preload of lunar-based two-dimensional turntable and system stiffness

WANG Zhi

Changchun Institute of Optics, Fine Mechanics and Physics,Chinese Academy of Sciences, Changchun 130033, China

Abstract

The relationship between bearing preload and system stiffness was investigated under the condition that the structure turntable was fixed. The relationships among bearing preload, bearing stiffness and shafting stiffness were analyzed. The computation formula between bearing preload and shafting natural frequency was deduced. Using finite element analysis the relationship curve between bearing preload and system natural frequency was obtained. Natural frequency tests of a two-dimensional turntable verified the validity of the proposed method, and an effective method was provided to determine the optimum bearing preload.

Keyword: mechanical design; extreme ultraviolet camera; two-dimensional turntable; bearing; preload; stiffness

Show Figures

0 引言

嫦娥三号月球着陆器对极紫外相机的刚度提出了很高的要求, 同时为了避免与卫星及着陆器的基频耦合, 要求极紫外相机发射方向基频大于70 Hz, 垂直于发射方向基频大于28 Hz。极紫外相机的刚度主要由二维转台的刚度决定, 在相机主体以及二维转台结构形式确定的情况下, 系统刚度的高低就与轴系刚度的高低有直接的关系。月基二维转台主要由俯仰、方位轴系组成, 大量级的振动、冲击以及低速工作的模式, 要求所用轴承有较高的轴向、径向刚度; 同时, 转台的指向精度还要求轴承具有高的定位精度和低的摩擦力矩。为保证月基二维转台的精度和刚度, 在工程实施上, 轴系多采用配对、能预紧的角接触球轴承^{[1, 2]}。

对配对使用的角接触球轴承施加合适的预紧力, 可以提高轴承刚度、轴系的旋转精度, 减小振动噪声, 消除轴向间隙。在安装轴承时, 如果实际预紧力大于最佳预紧力, 虽然可以获得较高的轴系刚度及抗卸载能力, 但却使轴承的摩擦力矩过大, 且容易出现“ 死点” , 导致温升加剧, 降低轴承寿命; 如果实际预紧力小于最佳预紧力, 虽然摩擦力矩小了, 但轴承刚度将不能满足系统刚度要求, 在较大的加速度作用下容易发生卸载, 出现间隙。因此施加预紧力的准确性对于轴承的性能以及系统的性能都有很大的影响。

为了保证极紫外相机二维转台的刚度、精度及可靠性要求, 本文在文献[3]工作的基础上对其轴承预紧力和系统刚度之间的关系进行分析, 推导出月基二维转台刚度与轴承预紧力之间关系的简化公式, 并通过有限元分析和试验验证了理论的正确性。

1 月基二维转台轴承的配置方式

单个角接触球轴承只能承受一个方向的轴向载荷, 在承受径向载荷时, 会引起附加轴向力, 必须施加相应的反向载荷。因此角接触球轴承需成对使用, 且通过轴向定位预紧以提高其刚度。

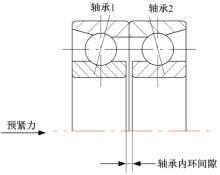
考虑嫦娥三号月球着陆器的力、热条件, 月基二维转台^{[4, 5]}(见图1)的俯仰、方位轴系轴承的配置均采用一端固定, 另一端游动的方式, 如图2所示。为了增加轴系的抗弯刚度, 月基二维转台俯仰、方位轴系固定端角接触球轴承均采用如图3所示的配对方式, 采用轴向定位预紧; 轴系的游动端采用深沟球轴承, 其内圈和轴之间可以滑动, 以消除温度变化引起的轴系变形。

	Figure Option View Download New Window
	图1 月基极紫外相机结构模型Fig.1 Model of optical-mechanical structure design for EUV camera

	Figure Option View Download New Window
	图2 轴系轴承配置方式Fig.2 Bearing configuration of shafting

	Figure Option View Download New Window
	图3 角接触轴承配置方式Fig.3 Partnership pattern of angle contact ball bearing

2 轴承预紧力与轴系刚度的关系

轴承的预紧力影响着轴承的刚度, 轴承的刚度影响着轴系的刚度, 而轴系的刚度又影响着整个系统的固有频率。因此通过分析轴承预紧力与轴承刚度的关系、轴系刚度的关系, 建立轴承预紧力与系统固有频率的关系表达式, 确定轴承的最佳预紧力。

2.1 轴承预紧力与轴承刚度关系分析

月基二维转台相机主体的质心设计在俯仰轴系的旋转轴上, 因此俯仰轴系受力简单, 静态情况下仅受径向负荷, 轴承径向刚度可以用简化计算公式^{[6, 7]}获得:

$\begin{matrix} K_{r} = 1.7164 D_{w}^{\frac{1}{3}} Z^{\frac{2}{3}} \frac{co s^{2} α}{si n^{\frac{1}{3}} α} F_{a 0}^{\frac{1}{3}} (1) \end{matrix}$

式中:D_w为钢球直径; Z为单个轴承钢球数目; α 为接触角; F_a0为所施加的轴向预紧力。

方位轴系仅受轴向载荷, 轴承轴向刚度可以用简化计算公式获得:

$\begin{matrix} K_{a} = 6.8658 \times 10^{6} {(Z^{2} D_{w} si n^{5} α)}^{\frac{1}{3}} F_{a 0}^{\frac{1}{3}} (2) \end{matrix}$

月基二维转台在设计时, 需要考虑系统的力学环境适应性(正弦、随机), 要能承受卫星发射过程、地月变轨以及月表着陆过程的振动、冲击。因此动态情况下, 需要分析在径向、轴向联合负荷作用下轴承的刚度, 采用近似计算方法的轴承刚度计算式为:

$\begin{matrix} \begin{matrix} K'_{a} \approx K_{a} (3) \\ 径向刚度为 : K'_{r} \approx 2 K_{r} (4) \end{matrix} \end{matrix}$

由轴承动态刚度的近似计算公式可以看出, 联合负荷情况下轴承的径向刚度为纯径向负荷条件下径向刚度的2倍左右。原因是轴向负荷的施加使原本只在径向负荷下近一半钢球承载的情况变成了几乎所有钢球承载, 因此轴承径向刚度成倍提高, 所以轴向预紧力有利于提高轴承的径向刚度。

2.2 轴承预紧力与轴系刚度的关系计算

2.2.1 轴系固有频率计算

(1)俯仰轴系固有频率计算

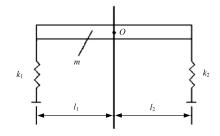
由前面的分析可以得知, 给配对使用的角接触球轴承施加合适的预紧力, 可以提高轴承的刚度, 进而提高轴系的刚度。而轴系的刚度可以由其固有频率来表征, 静态情况下俯仰轴系可以简化为如图4所示的弹簧质量系统, 该轴系的固有频率为^[8]:

$\begin{matrix} \begin{matrix} W_{n}^{2} = \frac{1}{2} (a + c) \mp \frac{1}{2} \sqrt{{(a - c)}^{2} + \frac{4 m b^{2}}{I}} \\ a = \frac{K_{1} + K_{2}}{m}, b = \frac{K_{2} l_{2} - K_{1} l_{1}}{m}, c = \frac{K_{1} l_{1}^{2} + K_{2} l_{2}^{2}}{m} \\ (5) \end{matrix} \end{matrix}$

式中:W_n=2π f, f为轴系固有频率; m为轴系质量; K₁、K₂分别为柔性元件1、2的刚度; l₁、l₂分别为柔性元件1、2相对于振动体中心O的距离, l=l₁+l₂; I为振动体的转动惯量。

	Figure Option View Download New Window
	图4 弹簧质量系统Fig.4 System of spring-mass

由式(5)可以看出, 俯仰轴系的固有频率取决于系统的质量、刚度及轴承的分布, 在图1所示的月基二维转台中, 轴系(含相机主体)的质量、转动惯量及轴承的分布都可以很容易计算。所以俯仰轴系的固有频率就取决于轴承的刚度, 即轴向定位预紧角接触球轴承的刚度。

(2)方位轴系固有频率计算

方位轴系仅受轴向载荷, 方位轴系的轴向振动模型如图5所示(图中C₁、C₂为阻尼), 可以得出方位轴系轴向刚度与固有频率的关系为^[9]:

$\begin{matrix} ω_{n}^{2} = K_{a} / m (6) \end{matrix}$

由式(6)可以看出, 方位轴系的固有频率取决于定位预紧角接触球轴承的刚度。

	Figure Option View Download New Window
	图5 轴系轴向振动模型Fig.5 Axial dynamic model of a shafting

2.2.2 轴承预紧力与轴系刚度的关系

(1)俯仰轴系

月基二维转台俯仰轴系所用角接触球轴承为71905AC, 由式(1)可知, 轴向定位预紧角接触球轴承的径向刚度与所施加的预紧力有关; 由式(5)可知, 轴系的刚度与相机主体的质量、角接触球轴承的刚度及分布有关。综合式(1)(5)可以得到轴承预紧力与轴系固有频率的关系为:

$\begin{matrix} \{\begin{matrix} F_{a 0} = \frac{f^{6} sinα}{40.45 π^{6} D_{w} Z^{2} B^{3} co s^{6} α} \\ B = (\frac{2}{m} + \frac{l_{1}^{2} + l_{2}^{2}}{I}) - {[(\frac{2}{m} - \frac{l_{1}^{2} + l_{2}^{2}}{I})}^{2} + \\ {\frac{4 {(l_{2} - l_{1})}^{2}}{Im}]}^{\frac{1}{2}} \end{matrix} (7) \end{matrix}$

(2)方位轴系

月基二维转台的方位轴系所用角接触球轴承为71815C, 轴承预紧力与轴系固有频率的关系为:

$\begin{matrix} F_{a 0} = \frac{f^{6} m^{3}}{2.07 \times 10^{22} π^{6} Z^{2} D_{w} si n^{5} α} (8) \end{matrix}$

由式(7)(8)可以看出, 在轴系结构已定的情况下, 轴承的预紧力与轴系的固有频率有关。

3 轴承预紧力与系统基频的关系

月基二维转台与相机主体的有限元模型如图6所示。

	Figure Option View Download New Window
	图6 系统有限元模型Fig.6 FEM of system

3.1 俯仰轴系轴承预紧力对系统基频的影响

在图6所示的整机有限元模型中, 对方位轴系角接触球轴承施加350 N预紧力, 对俯仰轴角接触球轴承施加不同预紧力。相机整机的一阶模态与俯仰轴系的角接触球轴承预紧力关系如表1所示。

表1 相机一阶模态与俯仰轴系轴承预紧力关系 Table 1 Relationship between preload of pitching bearing and first modal frequency of system

从表1可以看出, 在方位轴系轴承预紧力不变的情况下, 相机整机频率随俯仰轴系轴承预紧力的增大而提高。

3.2 方位轴系轴承预紧力对系统基频的影响

在图6所示的整机有限元模型中, 俯仰轴系轴承施加150 N预紧力, 对方位轴角接触球轴承施加不同预紧力。相机整机的一阶模态与方位轴系的角接触球轴承预紧力关系如表2所示。从表2可以得出, 在俯仰轴系轴承预紧力不变的情况下, 相机整机频率随方位轴系轴承预紧力的增大而提高。

表2 相机一阶模态与方位轴系轴承预紧力关系 Table 2 Relationship between preload of azimuth bearing and first modal frequency of system

3.3 整机模态

通过以上分析, 结合实际装配情况综合考虑整机模态分析时, 方位轴系预紧力施加350 N, 俯仰轴系预紧力施加120 N, 计算整机一阶模态为29.01 Hz。

4 试验验证

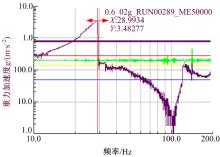
整机的固有频率测试试验如图7所示, 相机通过专用工装固定在振动台上, 通过对系统进行0.2g扫频获得系统的基频。图7中相机的振动方向为与卫星发射方向垂直的方向, 且该方向系统的基频最低, 图8为该方向的基频曲线。

	Figure Option View Download New Window
	图7 系统固有频率测试Fig.7 Test for first modal frequency of system

	Figure Option View Download New Window
	图8 试验方向一阶频率曲线Fig.8 Test curve of first modal frequency

5 结束语

为了满足嫦娥三号月球着陆器对月基二维转台提出的刚度要求, 在月基二维转台结构形式确定的情况下, 研究了提高系统刚度的措施。对配对使用的角接触球轴承施加合适的预紧力, 可以提高轴承的刚度, 进而提高支撑系统的刚度。基于该思路, 本文主要分析了轴承预紧力和轴承刚度、轴系刚度的关系, 推导出了轴承预紧力与轴系刚度的关系表达式, 并通过有限元分析的方法获得了轴承预紧力与整机固有频率的关系曲线。验证试验证明了理论的正确性, 并为确定轴承最佳预紧力提供了一个有效的方法。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	张景旭. 大型跟瞄架方位轴系的研制[J]. 光学精密工程, 1996, 4(2): 73-77. Zhang Jing-xu. Development of vertical axial system for large tracking and pointing mount[J]. Optics and Precision Engineering, 1996, 4(2): 73-77. [本文引用:1]
[2]	田学光, 田兴志, 刘轩, 等. 大型精密转台高精度角度微驱动装置研制[J]. 光学精密工程, 2010, 18(5): 1112-1118. Tian Xue-guang, Tian Xing-zhi, Liu Xuan, et al. Development of angular micro driving device for large-scale and high accurate turntable[J]. Optics and Precision Engineering, 2010, 18(5): 1112-1118. [本文引用:1]
[3]	韩德一, 梁波. 惯性平台轴承预紧力及其刚度的计算分析[J]. 中国惯性技术学报, 1998, 6(4): 39-43. Han De-yi, Liang Bo. Analysis and computation on the preloaded force and stiffness of bearing fixed in the inertial platform[J]. Journal of Chinese Inertial Technology, 1998, 6(4): 39-43. [本文引用:1]
[4]	王智, 李朝辉. 月基极紫外相机光机结构设计[J]. 光学精密工程, 2011, 19(10): 2427-2433. Wang Zhi, Li Zhao-hui. Optical-mechanical structure design for lunar-based extreme ultraviolet camera[J]. Optics and Precision Engineering, 2011, 19(10): 2427-2433. [本文引用:1]
[5]	李朝辉, 陈波. 月基对地观测跟踪转台设计与分析[J]. 光子学报, 2010, 39(12): 2215-2219. Li Zhao-hui, Chen Bo. Development of lunar pointing mounts for imaging to the earth[J]. Acta Photonica Sinica, 2010, 39(12): 2215-2219. [本文引用:1]
[6]	李为民, 王海涛. 轴向定位预紧轴承刚度计算[J]. 河北工业大学学报, 2001, 30(2): 15-19. Li Wei-min, Wang Hai-tao. Rigidity calculation of axial position preload bearings[J]. Journal of Hebei University of Technology, 2001, 30(2): 15-19. [本文引用:1]
[7]	方兵, 张雷, 曲兴田, 等. 角接触球轴承刚度理论计算与实验[J]. 吉林大学学报: 工学版, 2012, 42(4): 840-844. Fang Bing, Zhang Lei, Qu Xing-tian, et al. Theoretical and experimental research of stiffness of angular contact ball bearing[J]. Journal of Jilin University(Engineering and Technology Edition), 2012, 42(4): 840-844. [本文引用:1]
[8]	郭向东, 王燕霜. 轴承预紧力-系统固有频率及跨距关系的研究[J]. 轴承, 2013(4): 30-33. Guo Xiang-dong, Wang Yan-shuang. Research on relationship among bearing preload, system natural frequency and span[J]. Bearing, 2013(4): 30-33. [本文引用:1]
[9]	Shan Xiao-biao, Xie Tao, Chen Wei-shan. Novel approach for determining the optimal axial preload of a simulating rotary table spindle system[J]. Journal of Zhejiang University Science A, 2007, 8(5): 812-817. [本文引用:1]

1996

0.0

. 1996, 4(2):73-77

Development of vertical axial system for large tracking and pointing mount

大型跟瞄架方位轴系的研制

Zhang Jing-xu.

张景旭

Changchun Institute of Optics and Fine Mechanics, Chinese Academy of Sciences, ChangChun 130022

The development process of vertical axial system for large tracking and pointing mountare presented detailed in the paper. The design of axial system and large key parts is analyzedby determined or undetermined.

详细地叙述了大型跟瞄架方位轴系的研制过程,对轴系及关键大件的设计给出了定性及定量分析.

... 为保证月基二维转台的精度和刚度,在工程实施上,轴系多采用配对、能预紧的角接触球轴承^[1,2] ...

2010

0.0

. 2010, 18(5):1112-1118

Development of angular micro driving device for large-scale and high accurate turntable

大型精密转台高精度角度微驱动装置研制

Tian Xue-guang , Tian Xing-zhi , Liu Xuan

田学光, 田兴志, 刘轩

1.Changchun Institute of Optics, Fine Mechanics and Physics,Chinese Academy of Sciences, Changchun 130033,China; 2.Graduate University of Chinese Academy of Sciences, Beijing 100039, China

A high precision angular driving device was developed for a Large-Scale and High Accurate Turntable( its positioning accuracy should be less than 0.5″) for calibration and test of cameras. The whole structure of the turntable was introduced, and the principle and structure of the developed angular driving device were given in detail. By using a new angular displacement conversion mechanism, the angular driving device could convert the straight-line displacement into a angular displacement to obtain a high angular resolution. Meanwhile, the angular micro driving device scarcely generates the axial force or radial force to influence on the axis accuracy in driving turntable. Furthermore, a new positioning method combined coarse and fine positionings was proposed to improve the positioning accuracy, in which a torque motor was used for coarse positioning and the angular driving device for fine positioning. Finally, the angular resolution of the angular driving device was calculated and verified, results show that it is superior to 0.08″ and can meet the requirement of the turntable for positioning accuracy.

针对用于标定和检测的大型精密转台（要求其定位误差≤±0.5″），研制了高精度角度微驱动装置。介绍了转台的总体结构，给出了角度微驱动装置的驱动原理和构成。该角度微驱动装置主要通过一个角位移转换机构把精密直线位移转化为精密角位移来实现高的角度分辨率，其在驱动转台旋转的过程中几乎不给转台带来轴向力和径向力，因此不影响转台的轴系精度。为了满足定位要求，转台设计采用了粗精结合、二次定位的方法，即先采用力矩电机进行粗定位，然后使用角度微驱动装置来实现精定位。最后，从理论上计算了角度微驱动装置的分辨率并进行了测试和应用验证，证明此角度微驱动装置的分辨率优于0.08″,满足转台定位精度要求。

... 为保证月基二维转台的精度和刚度,在工程实施上,轴系多采用配对、能预紧的角接触球轴承^[1,2] ...

1998

0.0

2011

0.0

. 2011, 19(10):2427-2433 DOI:10.3788/OPE.20111910.2427

Optical-mechanical structure design for lunar-based extreme ultraviolet camera

月基极紫外相机光机结构设计

Wang Zhi , Li Zhao-hui.

王智, 李朝辉

Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun 130033, China

To monitor and research 30.4 nm radiation generated by the plasmasphere, a lunar-based Extreme Ultraviolet(EUV) camera was developed.A multilayer mirror optical system and a 30.4 nm photon counting detector were adopted as the main body of the camera, and a two-dimensional tracing mechanism drived by a stepping motor was used to trace the earth. Aim to the vibration and impact from the process of satellite launching, orbit changes from earth's to moon's, moon landing, and the cruel temperature environment of the moon, the optical-mechanical design of EUV camera gave a consideration to the environmental adaptability. After the optimization by finite element analysis,it shows that the first order resonant frequency of the optical-mechanical structure is 49.3 Hz with the mass less than 15 kg, the motion mechanism operates freely within -50~+80 ℃, and the mirror surface accuracy (RMS) is 13.44 nm(<14 nm) under the load of uniform temperature drop of 50℃. Those results meet the technical requirements of the camera.

为了对地球等离子体层产生的30.4 nm辐射进行全方位的长期监视和观测,研制了月基极紫外相机。相机主体采用多层膜单反射镜光学系统以及30.4 nm球面光子探测器的结构形式,跟踪机构采用俯仰-方位模式,由步进电机驱动实现对地球的捕获。针对卫星发射、地月变轨、月表着陆过程中的振动冲击以及月表残酷的温度环境,月基极紫外相机的光机结构设计考虑了环境(力学、温度)适应性,有限元分析结果表明,光机结构在整机质量<15 kg条件下,一阶谐振频率为49.3 Hz;运动机构在-50~+80 ℃运转自如;在50 ℃均匀温降载荷作用下反射镜面形精度RMS值为13.44 nm(<14 nm),满足相机的技术指标要求。

... 考虑嫦娥三号月球着陆器的力、热条件,月基二维转台^[4,5](见图1)的俯仰、方位轴系轴承的配置均采用一端固定,另一端游动的方式,如图2所示 ...

2010

0.0

. 2010, 39(12):2215-2219 DOI:10.3788/gzxb20103912.2215

Development of lunar pointing mounts for imaging to the earth

月基对地观测跟踪转台设计与分析

Li Zhao-hui , Chen Bo.

李朝辉, 陈波

（Changchun Institute of Optics,Fine Mechanics and Physics,Chinese Academy of Sciences,Changchun 130033,China）

Aiming at the mechanical condition during the moon landing,complex environment lunar surface features,and strict weight requirements,a tracking turntable for lunar-based earth observation was designed which consists of two main components: horizontal shaft and elevation actuator modules,and vertical shaft and azimuth actuator modules.In addition,Hour sensors were selected as the rotation position detector of elevation and azimuth shafts,and the pointing accuracy is better than 0.1°.An effective tracking turntable design configuration,optimized structure of supporter and selection of material were performed based on the finite element analysis method,and the stiffness of axis system and transmission accuracy of actuator module were analyzed to obtain the trade-off design with better capabilities of deep space environmental adaptability.To qualify the design for the specific mission requirements,the vibration and thermal vacuum tests were carried out with the result of 41 Hz eigenfrequencies and the required running temperature changing range (—40℃~+80℃).The experimental results show that the proposed design has advantages of compact volume,light weight and high reliability.

针对登月过程严酷的力学条件、月球表面复杂的环境特征以及严格的重量要求,设计了一种可适用于月基观测的跟踪转台.该转台主要由水平轴系及驱动机构和竖直轴系及驱动机构组成,采用霍耳元件作为位置检测元件,其综合指向准确度≤0.1°.基于有限元分析方法确定转台结构方案、优化主要支撑件结构及合理选材,并对驱动机构与轴系对转台刚度、温度适应性和指向准确度的影响做了深入分析与计算.同时进行了整机的力学模拟试验和运动机构的高低温试验,一阶谐振频率为49 Hz,在-40 ℃ ～+80 ℃温度范围内工作正常.结果表明转台各项性能指标满足工程任务要求,具有结构紧凑、可靠性高、重量轻的特点.

... 考虑嫦娥三号月球着陆器的力、热条件,月基二维转台^[4,5](见图1)的俯仰、方位轴系轴承的配置均采用一端固定,另一端游动的方式,如图2所示 ...

2001

0.0

... 1 轴承预紧力与轴承刚度关系分析月基二维转台相机主体的质心设计在俯仰轴系的旋转轴上,因此俯仰轴系受力简单,静态情况下仅受径向负荷,轴承径向刚度可以用简化计算公式^[6,7]获得: ...

2012

0.0

. 2012, 42(4):840-844

Theoretical and experimental research of stiffness of angular contact ball bearing

角接触球轴承刚度理论计算与实验

Fang Bing , Zhang Lei , Qu Xing-tian

方兵, 张雷, 曲兴田

College of Mechanical Science and Engineering, Jilin University, Changchun 130022, China

The geometry of contact deformation for the rolling elements of angular contact ball bearing was described by coordinate transformation method. The analytical expression for the stiffness of angular contact ball bearing was derived according to the Hertzian elastic contact theory. The influences of preload, contact angle, etc. on the bearing stiffness were analyzed theoretically. A test bench was developed to measure the bearing stiffness. The comparison was carried out between the theoretical analysis and the experimental results.The results show that the discrepancy between the theoretical calculation and test data was less than 10%, meeting the requirement of engineering calculation.

采用坐标变换方法建立角接触球轴承滚动体接触变形的几何关系,根据Hertz弹性体接触理论推导了角接触球轴承刚度的解析表达式。理论分析了预紧力、接触角等对轴承刚度的影响。研制了轴承刚度测试实验台,将理论分析与实验结果进行了对比,结果表明:理论计算方法与实验结果的相对误差在10%以内,能够满足工程计算的需要。

2013

0.0

... 而轴系的刚度可以由其固有频率来表征,静态情况下俯仰轴系可以简化为如图4所示的弹簧质量系统,该轴系的固有频率为^[8]: ...

2007

0.0

... 方位轴系仅受轴向载荷,方位轴系的轴向振动模型如图5所示(图中C₁、C₂为阻尼),可以得出方位轴系轴向刚度与固有频率的关系为^[9]: ...