基于总线控制的面齿轮复杂曲面加工技术

引用本文

王延忠, 侯良威, 吕庆军, 赵兴福, 吴灿辉. 基于总线控制的面齿轮复杂曲面加工技术. 2015, 45(6): 1836-1843
WANG Yan-zhong, HOU Liang-wei, LYU Qing-jun, ZHAO Xing-fu, WU Can-hui. Processing technology of face gear complex surface based on bus control. Journal of Jilin University Engineering and Technology Edition, 2015, 45(6): 1836-1843 复制到剪切板

Permissions

基于总线控制的面齿轮复杂曲面加工技术

王延忠¹, 侯良威¹, 吕庆军², 赵兴福³, 吴灿辉⁴

1.北京航空航天大学机械工程学院,北京 100191

2.中国北方车辆研究所,北京 100072

3.中航工业哈尔滨东安发动机(集团)有限公司,哈尔滨 150066

4.中国航空综合技术研究所,北京100028

侯良威(1980-),男,博士研究生.研究方向:高精度面齿轮数控加工技术.E-mail:monkeymen@163.com

作者简介:王延忠(1963-),男,教授,博士.研究方向:机械传动复杂曲面数控加工.E-mail:YZWang63@126.com

基金:总装备部预研基金重点项目(9140A18020113HK010XX); 总装备部预先研究项目(513080202XX,513181200XX); 国家自然科学基金项目(51275020)

摘要

提出了一种基于EtherCAT总线的开放式多轴联动数控机床控制方式,研制了面齿轮专用数控加工设备。以面齿轮成形原理为基础,分析了蜗杆滚刀和碟片铣刀加工面齿轮的原理和方法,进行面齿轮数控加工坐标转换和刀位计算。给出了基于机床结构的面齿轮数控加工等价方法,进行面齿轮试件加工试验,通过pmm-c700三坐标测量机对试件产品进行齿面检测,得到面齿轮齿面点法向偏差范围,符合面齿轮齿型特点要求。验证了机床结构和加工方法的可行性,为面齿轮的工程化应用奠定了基础。

关键词: 机械制造自动化; 面齿轮加工; 总线控制; 刀位计算; 试验验证

中图分类号:TG659 文献标志码:A 文章编号:1671-5497(2015)06-1836-08

Processing technology of face gear complex surface based on bus control

WANG Yan-zhong¹, HOU Liang-wei¹, LYU Qing-jun², ZHAO Xing-fu³, WU Can-hui⁴

1.College of Mechanical Engineering, Beijing University of Aeronautics and Astronautics, Beijing 100191,China

2.China North Vehicle Research Institute, Beijing 100072,China

3.AVIC Harbin Dong'an Engine Corporation LTD., Harbin 150066,China

4.China Aero-polytechnology Establishment, Beijing 100028,China

Abstract

A control method for five-axle linkage CNC machine tools was proposed based on EtherCAT, and special CNC processing equipment for face gear was developed. The principles and methods of hopping and milling were analyzed on the basis of the principle of face gear cutting. The CNC processing coordinate conversion and tool path generation of hopping and milling were conducted. The CNC methods of processing were given based on the structure of the special face gear machine, and processing experiments of face gear were conducted. The coordinate values of tooth surface points were detected by pmm-c700 CMM, and the deviation ranges in the normal direction of face gear surface were obtained. The results verify that the structure of the machine and the processing methods are feasible, which lay the foundation of engineering applications of face gears.

Keyword: machinery manufacturing automation; face gear processing; bus control; tool path generation; experimental verification

Show Figures

0 引言

面齿轮是一种特殊的锥齿轮传动形式, 具有体积小、噪声低、承载能力大等优点, 国外己将面齿轮技术应用于航空航天和高性能车辆传动系统上。但由于其军事应用背景, 在面齿轮传动方面实行严格的技术封锁, 因此立足国内, 研究面齿轮传动技术及应用己势在必行。国外对面齿轮的研究开展较早, 目前己相当成熟, AGUSTA公司^[1]将面齿轮技术应用于航空传动中。NASA公司^{[2, 3]}将面齿轮传动技术应用于某型号直升机汇流-分流传动系统中。Fellow公司^[4]对面齿轮插齿加工进行了研究。GLEASON公司^[5]提出了CONIFACE磨削加工方法和设备。美国和欧洲相继开展了RDS-21^[6]和FACET^[7]等针对面齿轮研究的大型专项计划。国内在面齿轮研究方面开展较晚, 朱如鹏^[8]最早进行了面齿轮传动技术研究, 并开发出国内第一台面齿轮数控插齿加工机床。赵宁^{[9, 10]}开展了面齿轮滚齿加工技术研究, 提出基于普通数控机床的面齿轮滚齿加工。李大庆^[11]开展了磨削加工技术研究, 提出在叶片磨床上进行面齿轮磨齿加工。王延忠^{[12, 13]}对蜗杆滚刀的设计及面齿轮的加工进行了研究。

近年来, 国内面齿轮传动技术发展迅速, 但其工程化应用却进展缓慢, 加工设备和技术的滞后是其中一个重要原因。面齿轮作为一种复杂曲面的数控加工, 需要多轴联动控制来实现, 而数控系统作为多轴联动加工技术的基础, 成为复杂曲面加工中的重要组成部分, 总线技术以其开放性和互操作性的通信特点在工业控制领域得到了广泛的应用^{[14, 15]}。

本文以面齿轮数控加工原理为基础, 提出了一种基于EtherCAT总线的开放式多轴联动数控机床控制方式, 研制了面齿轮专用数控加工设备; 分析了蜗杆滚刀和碟片铣刀加工面齿轮的原理和方法; 进行了面齿轮数控加工坐标转换和刀位计算; 给出了基于机床结构的面齿轮数控加工等价方法。最后通过面齿轮试件加工试验验证了机床结构和加工方法的可行性。

1 面齿轮复杂曲面数控加工原理

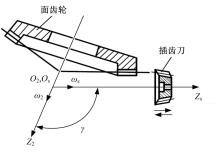
面齿轮齿面是由渐开线直齿轮形的插齿刀具展成切削得到, 插齿刀和面齿轮分别围绕自身轴线Z_s和Z₂以角速度ω _s和ω ₂旋转形成对滚运动, O_s和O₂为两轴线交点, 同时, 插齿刀做上、下往复的快速切削运动, 并逐渐做径向进给, 切出面齿轮齿形, 如图1所示, 当两轴线垂直相交时, 即轴交角γ =90° , 所得到的齿轮为正交面齿轮, 本文以正交面齿轮为例进行研究。

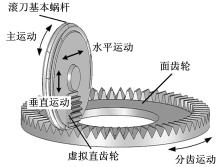
	Figure Option View Download New Window
	图1 面齿轮插齿加工原理Fig.1 Face gear shaper processing principle

插齿运动方式相对简单, 但由于其让刀过程的存在, 导致加工效率较低。由此出现了面齿轮蜗杆滚齿加工, 滚刀与面齿轮啮合传动可以看成滚刀与虚拟直齿轮啮合传动, 同时虚拟直齿轮又与面齿轮啮合传动, 如图2所示。

	Figure Option View Download New Window
	图2 面齿轮滚齿加工原理Fig.2 Face gear hobbing principle

滚齿加工时, 滚刀绕自身轴线旋转完成主运动, 面齿轮绕自身轴线旋转完成分齿运动, 两运动速度为定值; 水平进给运动是面齿轮滚刀沿工件径向的相对运动, 用来切出整个齿宽; 垂直进给运动是面齿轮滚刀沿工件轴向的相对运动, 用来切出整个齿高。

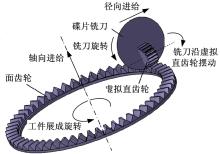
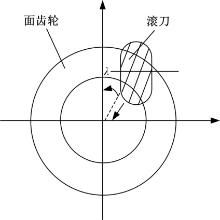
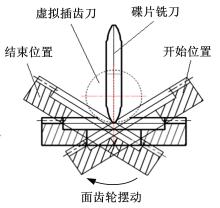
蜗杆滚刀加工面齿轮, 运动简单、效率高, 但由于蜗杆滚刀型面复杂, 制造难度大。由此出现了渐开线碟片铣刀铣齿加工, 直齿轮和渐开线碟片铣刀之间存在着虚拟的啮合关系, 即面齿轮齿面和渐开线碟片铣刀都可以看成是直齿轮齿面在空间运动的包络面, 如图3所示。

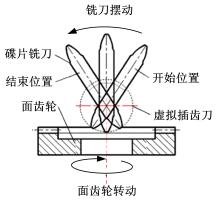
	Figure Option View Download New Window
	图3 正交面齿轮铣齿加工原理Fig.3 Orthogonal face gear milling principle

铣齿加工时, 碟片铣刀高速旋转模拟虚拟直齿轮的一个齿。面齿轮绕自身轴线旋转的同时, 铣刀绕虚拟直齿轮的轴线作旋摆运动, 两运动速度为定值, 同时铣刀沿径向和轴向进给, 即可实现面齿轮单齿全齿廓的展成加工。单齿完成后工件进行分度, 并重复以上动作, 直到完成面齿轮所有齿的铣齿加工。

2 基于EtherCAT总线的数控机床设计

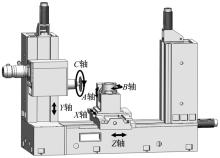
根据面齿轮数控加工原理进行面齿轮专用数控机床全新设计, 如图4所示, 机床包括X、Y、Z三个移动和A、B、C三个转动。沿机床导轨X方向的移动可以实现刀具的径向进给运动; 沿导轨Y方向的移动可以实现刀具的轴向进给运动; 沿导轨Z方向的移动可以实现刀具相对于面齿轮的附加运动; A方向转动可以实现刀具沿虚拟插齿刀轴线的摆动; B方向转动可以实现面齿轮的分齿运动; C方向为刀具自身的高速旋转运动。通过系统控制可以实现位置伺服和主轴功能等双重作用, 同时满足面齿轮的滚齿和铣齿加工以及后续的修形加工空间需求。

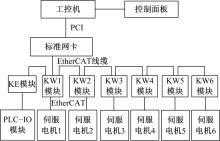
	Figure Option View Download New Window
	图4 面齿轮专用加工机床简图Fig.4 Sketch of processing machine of face gear

机床采用EtherCAT(工业以太网)总线控制方式, 不需要专业通信卡, 使用软件和标准以太网卡即可实现实时外部设备控制。标准网卡通过PCI与工控机连接, 另一端通过EtherCAT线缆与各控制模块连接, 控制模块与伺服电机连接, 其结构如图5和图6所示。

	Figure Option View Download New Window
	图5 控制系统硬件组成Fig.5 Hardware components of control system

	Figure Option View Download New Window
	图6 控制系统实物图Fig.6 Physical of control platform

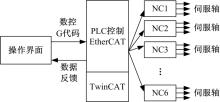
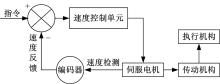
控制系统借助TwinCAT软件提供EtherCAT驱动程序, 利用其中的标准PLC语言开发功能, 对各项任务进行合理的划分, 并进行配置和连接, 接收操作界面数控G代码指令来控制各伺服轴, 其软件结构及电机伺服控制方式如图7和图8所示。

	Figure Option View Download New Window
	图7 系统基本软件结构Fig.7 Basic structure of system software

	Figure Option View Download New Window
	图8 控制伺服方式Fig.8 Control servo mode

3 面齿轮数控加工刀位计算

3.1 面齿轮滚齿加工刀位计算

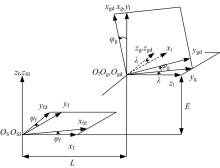
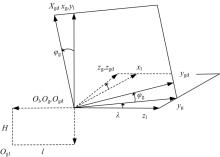
根据蜗杆滚刀加工面齿轮原理, 建立滚齿加工坐标系, 如图9所示。坐标系O_f(x_f, y_f, z_f)为面齿轮初始坐标系; O_fd(x_fd, y_fd, z_fd)为面齿轮绕轴z_f转动φ _f形成的动坐标系; 坐标系O_l(x_l, y_l, z_l)为坐标系O_f(x_f, y_f, z_f)平移后形成的临时坐标系, 两向平移距离分别为E和L; 坐标系O_g(x_g, y_g, z_g)为滚刀初始坐标系, 与坐标系O_l的夹角为λ ; 坐标系O_gd(x_gd, y_gd, z_gd)为滚刀绕轴z_g转动φ _g角度后形成的动坐标系。

	Figure Option View Download New Window
	图9 蜗杆滚刀加工面齿轮坐标系Fig.9 Worm hob processing coordinate system

从坐标系O_f到坐标系O_fd的转换矩阵为:

$\begin{matrix} M_{fd, f} = [\begin{matrix} \cos φ_{f} & \sin φ_{f} & 0 & 0 \\ - \sin φ_{f} & \cos φ_{f} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}] (1) \end{matrix}$

从坐标系O_l到坐标系O_f的转换矩阵为:

$\begin{matrix} M_{f, l} = [\begin{matrix} 0 & 0 & 1 & L \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & E \\ 0 & 0 & 0 & 1 \end{matrix}] (2) \end{matrix}$

从坐标系O_g到坐标系O_l的转换矩阵为:

$\begin{matrix} M_{l, g} = [\begin{matrix} 0 & sinλ & cosλ & 0 \\ 1 & 0 & 0 & 0 \\ 0 & cosλ & - sinλ & 0 \\ 0 & 0 & 0 & 1 \end{matrix}] (3) \end{matrix}$

从坐标系O_gd到坐标系O_g的转换矩阵为:

$\begin{matrix} M_{g, gd} = [\begin{matrix} \cos φ_{g} & \sin φ_{g} & 0 & 0 \\ - \sin φ_{g} & \cos φ_{g} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}] (4) \end{matrix}$

滚刀动坐标系O_gd到面齿轮动坐标系O_fd的转换矩阵为:

$\begin{matrix} \begin{matrix} M_{fd, gd} = M_{fd, f} \cdot M_{f, l} \cdot M_{l, g} \cdot M_{g, gd} = \\ [\begin{matrix} - cosΦsin φ_{g} & cosΦcos φ_{g} & sinΦ & \cos φ_{f} L \\ sinΦsin φ_{g} & - sinΦcos φ_{g} & cosΦ & - \sin φ_{f} L \\ \cos φ_{g} & \sin φ_{g} & 0 & E \\ 0 & 0 & 0 & 1 \end{matrix}] (5) \end{matrix} \end{matrix}$

式中:Φ =φ _f-λ ; E为滚刀半径与虚拟插齿刀半径的差值; L为面齿轮齿面径向位置差值; λ 为滚刀螺旋升角; φ _f为面齿轮转角; φ _g为滚刀转角, 且满足φ _fN_f=φ _gN_g。

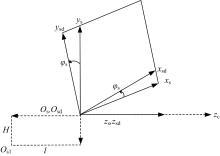
进行面齿轮滚齿加工时, 滚刀不仅与面齿轮工件作对滚运动。同时, 滚刀沿齿轮的齿长方向和齿高方向作修形运动, 以加工出完整的齿形。因此, 还需分析刀具的进给运动, 以得到刀具相对于工件完全展成刀位。建立滚刀进给坐标系, 如图10所示。

	Figure Option View Download New Window
	图10 滚齿加工进给坐标系Fig.10 Hobbing coordinate movement

图10中, 坐标系O_g1是由坐标系O_gd经过平移后得到的, 两向平移距离分别为H和l, H为面齿轮齿深, l为面齿轮径向齿长。

从坐标系O_g1到坐标系O_gd的转换矩阵为:

$\begin{matrix} M_{gd, g 1} = [\begin{matrix} 1 & 0 & 0 & - H \\ 0 & 1 & 0 & - l \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}] (6) \end{matrix}$

任意时刻, 刀具坐标系O_g1相对于面齿轮坐标系O_fd的转换矩阵为:

$\begin{matrix} M_{fd, g 1} = M_{fd, gd} \cdot M_{gd, g 1} (7) \end{matrix}$

由此可以得到, 面齿轮滚齿加工过程中的刀位为工件转角φ _f、径向进给运动距离l、齿深方向进给距离H的函数, 因此通过控制这三个参数即可实现面齿轮的数控精密加工。

3.2 面齿轮铣齿加工刀位计算

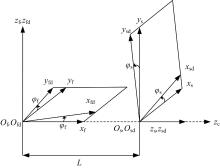
根据碟片铣刀加工面齿轮原理, 建立碟片铣刀加工坐标系如图11所示, 坐标系O_f(x_f, y_f, z_f)为面齿轮初始坐标系; O_fd(x_fd, y_fd, z_fd)为面齿轮绕轴z_f转动φ _f形成的动坐标系; 坐标系O_s(x_s, y_s, z_s)为铣刀初始坐标系; O_sd(x_sd, y_sd, z_sd)为铣刀绕虚拟插齿刀轴线z_c转动φ _s形成的动坐标系, 坐标原点O_f到O_s的距离为L。

	Figure Option View Download New Window
	图11 碟片铣刀加工面齿轮坐标系Fig.11 Disc cutter processing coordinate system

从坐标系O_f到坐标系O_fd的转换矩阵为:

$\begin{matrix} M_{fd, f} = [\begin{matrix} \cos φ_{f} & \sin φ_{f} & 0 & 0 \\ - \sin φ_{f} & \cos φ_{f} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}] (8) \end{matrix}$

从坐标系O_s到坐标系O_f的转换矩阵为:

$\begin{matrix} M_{f, s} = [\begin{matrix} 0 & 0 & 1 & L \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}] (9) \end{matrix}$

从坐标系O_sd到坐标系O_s的转换矩阵为:

$\begin{matrix} M_{s, sd} = [\begin{matrix} \cos φ_{s} & - \sin φ_{s} & 0 & 0 \\ \sin φ_{s} & \cos φ_{s} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}] (10) \end{matrix}$

从砂轮坐标系O_sd到面齿轮坐标系O_fd的转换矩阵为:

$\begin{matrix} \begin{matrix} M_{fd, sd} = M_{fd, f} \cdot M_{f, s} \cdot M_{s, sd} = \\ [\begin{matrix} \sin φ_{f} \cos φ_{s} & - \sin φ_{f} \sin φ_{s} & \cos φ_{f} & \cos φ_{f} L \\ \cos φ_{f} \cos φ_{s} & - \cos φ_{f} \sin φ_{s} & - \sin φ_{f} & - \sin φ_{f} L \\ \sin φ_{s} & \cos φ_{s} & 0 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}] (11) \end{matrix} \end{matrix}$

式中:φ _f为面齿轮转角; φ _s为铣刀绕虚拟插齿刀轴线z_c的转角。

同理, 进行面齿轮铣齿加工时, 铣刀沿齿轮的齿长方向和齿高方向作修形运动, 以加工出完整的齿形。建立铣刀进给坐标系, 如图12所示。

	Figure Option View Download New Window
	图12 铣齿加工进给坐标系Fig.12 Milling coordinate movement

坐标系O_s1是由坐标系O_sd经过平移后得到的, 两向平移距离分别为H和l。

从坐标系O_s1到坐标系O_sd的转换矩阵为:

$\begin{matrix} M_{sd, s 1} = [\begin{matrix} 1 & 0 & 0 & - H \\ 0 & 1 & 0 & - l \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}] (12) \end{matrix}$

任意时刻, 刀具坐标系O_s1相对于面齿轮坐标系O_fd的转换矩阵为:

$\begin{matrix} M_{fd, s 1} = M_{fd, sd} \cdot M_{sd, s 1} (13) \end{matrix}$

由此可以得到, 面齿轮滚刀加工过程中的刀位为工件转角φ _f、径向进给运动距离l、齿深方向进给距离H的函数, 因此通过控制这3个参数即可实现面齿轮的数控精密加工。

4 面齿轮数控加工方法和试验

4.1 数控滚齿加工

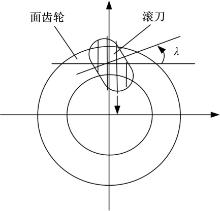
滚齿加工时由于存在滚刀螺旋升角, 使得滚刀轴线必须绕面齿轮端面旋转一个螺旋升角的角度, 如图13所示。实际加工时, 基于机床结构, 采用工件不动, 刀具相对于原来位置偏置一个距离, 如图14所示。举例说明, 面齿轮设计参数如表1所示。

	Figure Option View Download New Window
	图13 面齿轮滚齿加工运动方法Fig.13 Hobbing movement sports method

	Figure Option View Download New Window
	图14 面齿轮滚齿实际加工方法Fig.14 Face gear hobbing actual method

表1 面齿轮设计参数 Table 1 Face gear design parameters

由滚齿加工方法编制数控G代码, 输入数控系统, 进行面齿轮滚齿加工, 如图15所示。

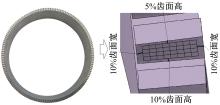
	Figure Option View Download New Window
	图15 面齿轮滚齿加工Fig.15 Face gear hobbing process

成品试件在pmm-c700三坐标测量机上进行检测。检测区域选择在距齿顶5%, 距齿根和内外端为10%的区域, 在此区域内齿宽方向取9个点, 齿高方向取5个点, 共计45个点, 如图16所示。

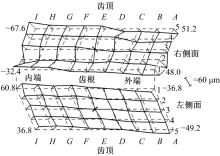
	Figure Option View Download New Window
	图16 面齿轮检测区域(滚齿)Fig.16 Face gear detection regionalism(hobbing)

检测各点坐标值, 经坐标变换与齿面点理论坐标值进行比较, 得到滚齿后的面齿轮实际齿面点网格的三维形貌图如图17所示, 齿面网格节点处的法向偏差如图18所示。

	Figure Option View Download New Window
	图17 齿面网格三维形貌图(滚齿)Fig.17 Three-dimensional grid topography(hobbing)

	Figure Option View Download New Window
	图18 法向偏差示意图(滚齿)Fig.18 Tooth surface deviation schematic(hobbing)

从图18可以看出, 实际齿面与理论齿面符合较好, 全齿面法向偏差范围为-67.6~78.8 μ m, 原因是滚刀本身制造误差和试件加工过程中存在一定误差。

4.2 数控铣齿加工

铣齿加工时, 渐开线碟片铣刀相对于面齿轮绕虚拟插齿刀轴线摆动, 由此加工时, 采用刀具不动, 工件绕虚拟插齿刀轴线摆动来完成, 如图19和图20所示。举例说明, 面齿轮设计参数如表2所示。

	Figure Option View Download New Window
	图19 面齿轮铣齿加工运动Fig.19 Milling movement sports

	Figure Option View Download New Window
	图20 面齿轮铣齿加工方法Fig.20 Face gear milling method

表2 面齿轮设计参数 Table 2 Face gear design parameters

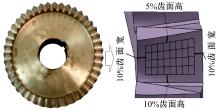
由铣齿加工方法编制数控G代码, 输入数控系统, 进行面齿轮铣齿加工, 如图21所示。同理, 对试件检测区域进行规划, 如图22所示。

	Figure Option View Download New Window
	图21 面齿轮铣齿加工Fig.21 Face gear milling process

	Figure Option View Download New Window
	图22 面齿轮检测区域(铣齿)Fig.22 Face gear detection regionalism(milling)

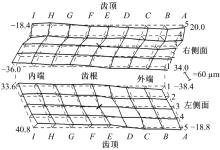
检测得到铣齿后的面齿轮实际齿面点网格三维形貌图如图23所示, 齿面网格节点处的法向偏差如图24所示。

	Figure Option View Download New Window
	图23 齿面网格三维形貌图(铣齿)Fig.23 Three-dimensional grid topography(milling)

	Figure Option View Download New Window
	图24 法向偏差示意图(铣齿)Fig.24 Tooth surface deviation schematic(milling)

从图24可以看出, 实际齿面与理论齿面吻合较好, 全齿面法向偏差为-38.4~48.0 μ m, 原因是加工过程中存在机床运动误差和铣刀本身制造误差。

5 结论

(1)提出了基于EtherCAT总线的面齿轮专用加工机床控制方式, 摆脱了复杂零件数控加工对现有成型数控系统的依赖, 解决了程序二次开发受限的问题。

(2)研制了面齿轮专用数控加工机床, 通过试件加工并进行齿面检测, 得到面齿轮齿面点网格三维形貌和齿面法向偏差, 面齿轮实际齿面与理论齿面符合较好, 在不考虑误差影响的情况下, 验证了机床结构的合理性和方法的可行性。

(3)面齿轮滚齿和铣齿加工中的影响参数有φ _g、l和H, 根据不同的加工要求, 合理选择这些参数值, 通过加工得到相应的面齿轮。

(4)面齿轮采用蜗杆滚刀加工时, 控制方式简单, 加工面齿轮精度受滚刀制造精度影响较大; 而采用碟片铣刀加工时, 控制方式相对复杂, 但铣刀本身制造简单, 面齿轮加工精度容易保证。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Litvin F L. Face gear drive with helical involute pinion: geometry, generation by a shaper and a worm, avoidance of singularities and stress analysis[R]. Washington: NASA, 2005. [本文引用:1]
[2]	Chen Y D, Bossler R B. Design analysis and testing methods for a split torque face-gear transmission[C]∥31th AIAA/SAE/ASME/ASEE Joint Propulsion Conference and Exhibit, San Diego, CA, 1995: 1-7. [本文引用:1]
[3]	Lewicki D G, Dempsey P J, Heath F G, et al. Gear fault detection effectiveness as applied to tooth surface pitting fatigue damage[R]. Washington: NASA, 2007. [本文引用:1]
[4]	Litvin F L. Gear Geometry and Applied Theory[M]. New jersey: PTR Prentice Hall, 1994. [本文引用:1]
[5]	Hermann D, Stadtfeld J. CONIFACE face gear cutting and grinding[J]. Gear Solutions, 2010(9): 38-47. [本文引用:1]
[6]	Lewichi D G, Heath G F, Filler R R, et al. RDS-21 face gear surface durability tests[R]. American Helicopter Society International Forum, ARL-TR-4089, 2007. [本文引用:1]
[7]	Guingand M, Vaujany J P, Jaquin C Y. Quasi-static analysis of a face gear under torque[J]. Computer Methods in Applied Mechanics and Engineering, 2005, 194(39-41): 4301-4318. [本文引用:1]
[8]	朱如鹏, 高德平. 面齿轮传动的研究现状与发展[J]. 南京航空航天大学学报, 1997, 29(3): 357-362. Zhu Ru-peng, Gao De-ping. Current state and development of research on face gear drive[J]. Journal of Nanjing University of Aeronautics and Astronautics, 1997, 29(3): 357-362. [本文引用:1]
[9]	Zhao Ning, Guo Hui, Fang Zong-de, et al. Research on machining face gear using a CNC hobbing machine[J]. Advanced Materials Research, 2010, 97(101): 3761-3764. [本文引用:1]
[10]	赵宁, 郭辉, 方宗德, 等. 用球形滚刀滚切面齿轮的理论误差[J]. 航空动力学报, 2009, 24(3): 677-682. Zhao Ning, Guo Hui, Fang Zong-de, et al. Theory error of cutting face gears with sphericity hob[J]. Journal of Aerospace Power, 2009, 24(3): 677-682. [本文引用:1]
[11]	李大庆. 直齿面齿轮啮合性能预控及碟形砂轮磨齿关键技术研究[D]. 镇江: 江苏大学机械工程学院, 2013. Li Da-qing. Research on precontrol method of meshing behavior and key technologies for grinding face gear by dish wheel[D]. Zhenjiang: School of Mechanical Engineering, Jiangsu University, 2013. [本文引用:1]
[12]	王延忠, 吴灿辉, 葛旭阳. 面齿轮滚刀基本蜗杆的设计方法[J]. 北京航空航天大学学报, 2009, 35(2): 166-169. Wang Yan-zhong, Wu Can-hui, Ge Xu-yang. Basalworm designing method of face gear hob[J]. Journal of Beijing University of Aeronautics and Astronautics, 2009, 35(2): 166-169. [本文引用:1]
[13]	Wang Yan-zhong, Hou Liang-wei, Liu Yan-qing, et al. Research on machining method of complex surface face gears[J]. Applied Mechanics and Materials, 2012, 163: 233-237. [本文引用:1]
[14]	刘清建, 王太勇, 徐跃, 等. 基于总线架构的多层次监控开放数控系统[J]. 吉林大学学报: 工学版, 2010, 40(6): 1589-1594. Liu Qing-jian, Wang Tai-yong, Xu Yue, et al. Multilayer monitoring and open CNC system based on fieldbus[J]. Journal of Jilin University(Engineering and Technology Edition), 2010, 40(6): 1589-1594. [本文引用:1]
[15]	吴坚, 李亚彬, 李静, 等. 基于SAEJ1939协议的汽车驱动力控制CAN总线[J]. 吉林大学学报: 工学版, 2009, 39(4): 855-858. Wu Jian, Li Ya-bin, Li Jing, et al. CAN bus of automotive driving force control system based on SAE protocol J1939[J]. Journal of Jilin University(Engineering and Technology Edition), 2009, 39(4): 855-858. [本文引用:1]

2005

0.0

... 国外对面齿轮的研究开展较早,目前己相当成熟,AGUSTA公司^[1]将面齿轮技术应用于航空传动中 ...

1995

0.0

... NASA公司^[2,3]将面齿轮传动技术应用于某型号直升机汇流-分流传动系统中 ...

2007

0.0

... NASA公司^[2,3]将面齿轮传动技术应用于某型号直升机汇流-分流传动系统中 ...

1994

0.0

... Fellow公司^[4]对面齿轮插齿加工进行了研究 ...

2010

0.0

... GLEASON公司^[5]提出了CONIFACE磨削加工方法和设备 ...

2007

0.0

... 美国和欧洲相继开展了RDS-21^[6]和FACET^[7]等针对面齿轮研究的大型专项计划 ...

2005

0.0

... 美国和欧洲相继开展了RDS-21^[6]和FACET^[7]等针对面齿轮研究的大型专项计划 ...

1997

0.0

... 国内在面齿轮研究方面开展较晚,朱如鹏^[8]最早进行了面齿轮传动技术研究,并开发出国内第一台面齿轮数控插齿加工机床 ...

2010

0.0

... 赵宁^[9,10]开展了面齿轮滚齿加工技术研究,提出基于普通数控机床的面齿轮滚齿加工 ...

2009

0.0

... 赵宁^[9,10]开展了面齿轮滚齿加工技术研究,提出基于普通数控机床的面齿轮滚齿加工 ...

2013

0.0

... 李大庆^[11]开展了磨削加工技术研究,提出在叶片磨床上进行面齿轮磨齿加工 ...

2009

0.0

. 2009, 35(2):166-169

Basalworm designing method of face gear hob

面齿轮滚刀基本蜗杆的设计方法

Wang Yan-zhong , Wu Can-hui , Ge Xu-yang.

王延忠, 吴灿辉, 葛旭阳

School of Mechanical Engineering and Automation, Beijing University of Aeronautics and Astronautics, Beijing 100191, China

Face-gear drives become the main direction of research for aeronautical drives because of their special advantages. The applied coordinate systems of face-gear were set up and the equation of face-gear tooth surface was established, then the face-gear tooth surface constrain conditions for dedendum undercutting and addendum pointing were analyzed based on the face-gear transmission theory, at the same time, the disciplines were discussed on the relationships between pressure angle and the face-gear outer & inner radius in keeping with the practically calculated examples. The calculating results are useful for designing the face-gear drive. In the end, the face-gear hobbing theory was analyzed, according to the gear geometry and applied theory, the hobbing surface equation was founded. The discrete values of three-dimensional coordinates for the hobbing surface were calculated by using the method of numerical calculation. The three-dimensional basal worm model of face-gear hob was designed by recurring to the three-dimensional software.

面齿轮传动由于其独特的传动优点,成为航空传动的主要研究方向.根据面齿轮传动原理,建立面齿轮加工坐标系,得到了面齿轮齿面方程,分析了面齿轮齿顶变尖和齿根根切的限制条件,同时根据实际算例讨论了面齿轮内外半径随压力角变化的规律,所获得的结论对面齿轮的设计具有参考价值.最后分析面齿轮的滚切原理,根据齿轮啮合原理,建立面齿轮滚刀型面方程,采用数值计算方法,得到滚刀型面离散三维坐标值,借助三维造型软件得到面齿轮滚刀基本蜗杆三维模型.

... 王延忠^[12,13]对蜗杆滚刀的设计及面齿轮的加工进行了研究 ...

2012

0.0

... 王延忠^[12,13]对蜗杆滚刀的设计及面齿轮的加工进行了研究 ...

2010

0.0

. 2010, 40(6):1589-1594

Multilayer monitoring and open CNC system based on fieldbus

基于总线架构的多层次监控开放数控系统

Liu Qing-jian , Wang Tai-yong , Xu Yue

刘清建, 王太勇, 徐跃

Tianjin Key Laboratory of Advanced Manufacturing Technologies and Equipments,Tianjin University, Tianjin |300072,China

Facing the trends of the computerized numerical control(CNC) systems towards multifunction and high integration possible leading to realtimeness and robustness problems caused by condensed information exchange, an open CNC system configuration was proposed based on ProfibusDP and PXI buses. The time behavior of the buses was analyzed, it was found they meet the demand for high speed and high precision. The controller uses the IPC framework, accomplishes the software function using the component technology, realize the rapid reconstruction of CNC by different allocation of functional components. The functions of state monitoring, failure diagnosis and processing optimization are fused into the CNC system using a 3layer network. The prototyped machine based on IPC framework proved the feasibility of the CNC scheme.

提出了一种基于ProfibusDP总线与PXI总线的开放式数控系统的设计方案。对总线的时间特性进行了分析,其满足数控系统加工控制高速度、高精度的要求。控制器采用IPC架构，通过对功能单元的不同配置实现数控系统的快速重构。同时，基于网络技术,采用三层集成监控的模式，将状态监测、故障诊断、加工优化等技术融合到数控系统中。最后，利用已开发出的原型机验证了方案的可行性。

... 面齿轮作为一种复杂曲面的数控加工,需要多轴联动控制来实现,而数控系统作为多轴联动加工技术的基础,成为复杂曲面加工中的重要组成部分,总线技术以其开放性和互操作性的通信特点在工业控制领域得到了广泛的应用^[14,15] ...

2009

0.0