基于模糊自适应的BP神经网络动态行驶车辆车长测算

引用本文

李寿涛, 田微, 郭鹏程, 马用学, 张浩, 王楠. 基于模糊自适应的BP神经网络动态行驶车辆车长测算. 2015, 45(6): 1881-1886
LI Shou-tao, TIAN Wei, GUO Peng-cheng, MA Yong-xue, ZHANG Hao, WANG Nan. Dynamic traveling vehicle length measurement based on fuzzy adaptive of BP neural network. Journal of Jilin University Engineering and Technology Edition, 2015, 45(6): 1881-1886 复制到剪切板

Permissions

基于模糊自适应的BP神经网络动态行驶车辆车长测算

李寿涛¹, 田微¹, 郭鹏程¹, 马用学¹, 张浩², 王楠³

1.吉林大学通信工程学院,长春 130022

2.吉林大学计算机科学与技术学院, 长春 130012

3.吉林大学汽车工程学院,长春 130022

张浩(1971-),男,副教授,博士.研究方向:模式识别及信息安全,生物信息学.E-mail:zhangh@jlu.edu.cn

作者简介:李寿涛(1975-),男,副教授,博士.研究方向:智能机械及机器人多智能体行为协调与控制,汽车系统动力学与控制.E-mail:list@jlu.edu.cn

基金:吉林省交通厅科技项目(2010-01-04); 吉林省产业技术研究与开发专项项目(2015Y062)

摘要

在对绿色通道检测系统实测大量数据分析及实验研究的基础上,提出了一种在车辆动态行驶过程中运用BP神经网络进行车长测算的方法。该方法通过模糊自适应的方式调节BP神经网络的学习率以加快算法的收敛速度。本文将该方法应用于吉林省省际收费站的绿色通道检测系统中,通过对绿通车辆大量的实车数据的测试与验证,结果表明本文所提测算方法能够有效地提高在车辆动态穿行过程中车长的测算精度。

关键词: 自动控制技术; BP神经网络; 动态行驶车辆; 车长测算; 学习率

中图分类号:TP183 文献标志码:A 文章编号:1671-5497(2015)06-1881-06

Dynamic traveling vehicle length measurement based on fuzzy adaptive of BP neural network

LI Shou-tao¹, TIAN Wei¹, GUO Peng-cheng¹, MA Yong-xue¹, ZHANG Hao², WANG Nan³

1.College of Communication Engineering, Jilin University, Changchun 130022, China

2.College of Computer Science and Technology, Jilin University, Changchun 130012, China

3.College of Automotive Engineering,Jilin University,Changchun 130022,China

Abstract

Based on the analysis of large number of measured data obtained from a free toll lane of highway detection system and experimental research, a vehicle length measurement method is proposed based on BP neural network, which can measure the length when the vehicle is traveling. This method can accelerate the convergent speed of BP neural network by fuzzy adaptively adjusting the learning rate of BP neural network. A large number of real vehicle data have been obtained after this method was applied to the detection system in the highway toll lane of Lalin River, an exit of Jilin Province to Heilongjiang Province. The results show that the proposed method of dynamic vehicle length measurement can effectively improve the measuring precision of traveling vehicles.

Keyword: automatic control technology; BP neural network; dynamic vehicle; vehicle length measurement; learning rate

Show Figures

0 引言

目前通常采用吨位法^[1]和无损检测法^[2]等技术对过往高速公路绿色通道的车辆进行检测, 然而这些方法往往需要对过往车辆或车厢长度进行测量, 对于车辆车长的测量, 传统方法是进行静态测量, 该方法准确度虽然很高, 但是达不到实时性要求, 同时还存在着很大的缺点, 如耗时、需要大量人力、容易造成道路拥堵等, 因此需要在货车通过绿色通道检测系统过程中能动态并精确地测算出车辆车长。

目前对运动物体实时测量的方法主要有光切法^[3]和机器视觉法^[4], 但由于我国高速公路上行驶的很多车辆都经过改装, 车身表面不规则、不平整, 使得运用这些方法测量的车长误差较大。

本文在绿色通道检测系统^[5]的基础上, 通过对大量实测数据的分析, 提出一种基于模糊逻辑自适应调节学习率的BP神经网络对动态行驶车辆车长进行测算的方法, 最后通过实验验证该方法能够有效地提高测算精度。

1 问题的提出

由于绿色通道检测系统的车道比较窄, 并且车道两边安装有射线机防护室和线阵机防护室, 这使得大型绿色通道车辆通过检测区域时, 驾驶员会非常谨慎小心, 通过时的速度会急速降低并变化。

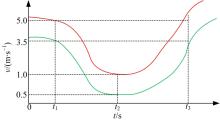
在对驾驶员的驾驶行为进行分析的基础上, 对现场大量的绿色通道车辆进行了测试, 得知当绿色通道车辆通过检测区域时, 车速会在一定范围变化, 其变化规律大致如图1中^[5]“ U型” 曲线带所示。图中t₁为驾驶室到达射线机防护室的时间点; t₂为驾驶室完全通过整个射线机防护室时的时间点; t₃为车厢完全驶离检测区域时的时间点。绿色通道车辆在进入检测车道直到驾驶室到达射线机防护室时, 车辆基本是匀速通过, 车速维持在3.5~5 m/s; 当车辆驾驶室到达射线机防护室时, 驾驶员调整车身减速通过, 这个过程车速会减小到0.5~1 m/s; 当驾驶室通过整个射线机防护室时, 车速逐渐加大, 在车厢完全通过整个射线机防护室时车速基本达到3.5~5 m/s; 之后车辆加速驶离检测区域。

	Figure Option View Download New Window
	图1 车辆速度变化规律曲线Fig.1 Vehicle speed variation curve

绿色通道车辆在通过检测区域的过程中, 由于要受到外界条件和驾驶员驾驶习惯的影响, 使得车辆通过检测区域的速度是非匀速的, 故不能简单利用时间与速度的关系来计算车辆长度, 这就使得测算动态行驶车辆的车长具有很大困难。

本文作如下定义:T₁和V₁分别为货车驾驶室前端从光电传感器节点一位置行驶到光电传感器节点二位置的时间和平均速度; T₂和V₂分别为货车驾驶室前端从光电传感器节点二位置行驶到光电传感器节点三位置的时间和平均速度; T_K为货车车头与车厢之间缝隙通过光电传感器节点一位置的时间; T_X为货车货箱部位通过光电传感器节点一位置的时间。

2 BP神经网络模型的建立及动态车辆车长测算

2.1 BP神经网络模型的建立

设输入学习样本为p个:x(1), …, x(p), 已知与其对应的导师为t(1), …, t(p), 学习算法是根据实际的输出y(1), …, y(p)与t(1), …, t(p)的误差E(称作总体误差)来修改由其连接权值和阈值构成的权向量w, 使得y(1), …, y(p)与t(1), …, t(p)尽可能地接近; 在此, 总体误差E被看作是权向量w的函数, 即E=E(w)^{[6, 7]}。

设输入的学习样本集为I^α={ $\begin{matrix} {V_{1}}^{α} \end{matrix}$ , $\begin{matrix} {V_{2}}^{α} \end{matrix}$ , $\begin{matrix} {T_{1}}^{α} \end{matrix}$ , $\begin{matrix} {T_{2}}^{α} \end{matrix}$ , $\begin{matrix} {T_{K}}^{α} \end{matrix}$ , $\begin{matrix} {T_{X}}^{α} \end{matrix}$ }, 对应的导师信号为L^α, 在此用这α 个样本对(I^α, L^α)对网络进行训练^[8]。对应于第m(m=1, 2, …, α )个样本的实际输出值为y^m, 定义第m个样本的神经网络学习误差函数如下:

$\begin{matrix} E_{m} = \frac{1}{2} {(L^{m} - y^{m})}^{2} (1) \end{matrix}$

所有α 个样本经正向传递运算后, 网络总误差为:

$\begin{matrix} E_{Σ} = \sum_{m}^{=} E_{m} = \frac{1}{2} \overset{α}{\sum_{m = 1}} (L^{m} - y^{m})^{2} (2) \end{matrix}$

如果网络误差大于设定的允许期望值, 则应用最速下降法, 反向调整各层连接权值, 使得误差达到最小。反向传播算法以误差修正学习规则对神经元权值进行调整, 即:

$\begin{matrix} \begin{matrix} w_{ij} (n + 1) = w_{ij} (n) + Δω (3) \\ Δω = - η \frac{\partial E_{Σ}}{\partial w} = - η \overset{α}{\sum_{m = 1}} \frac{\partial E_{m}}{\partial w} (4) \end{matrix} \end{matrix}$

式中:η > 0是学习率参数, 该参数用来调节神经网络搜索最优权值的速度和振荡程度; n为迭代次数; ω 为网络任意两个神经元之间的连接权值; w_ij为网络第i层到第j层的连接权值; Δ ω 为神经元之间的连接权值变化增量。

等效误差按上述推导过程由输出层向输入层反向传播产生, 经过多次调整网络误差最终收敛于期望误差。

用BP神经网络算法进行动态车辆车长测算数据处理的原理是:构建一个由6个节点(T₁、V₁、T₂、V₂、T_K和T_X)的输入层和一个节点(静态车长L)的输出层组成的三层BP神经网络模型, 可表示为六元函数f(V₁, V₂, T₁, T₂, T_K, T_X), 用通过实验获得的样本数据在Matlab上进行多次训练构建六输入单输出的神经网络, 如果训练结果达到系统的误差要求, 则可以确定输出各隐含层和输出层的权值和阈值, 然后就可以利用训练好的网络参数, 根据测得的数据, 获得较为精确的车辆车长。

隐含层选用如下所示的双曲正切型函数tansig:

$\begin{matrix} f (x) = \frac{2}{1 + e^{- x}} - 1 = \frac{1 - e^{- x}}{1 + e^{- x}} (5) \end{matrix}$

输出层选用如下所示的线型函数purelin:

$\begin{matrix} f (x) = x (6) \end{matrix}$

2.2 基于模糊逻辑自适应调节学习率的动态行驶车辆车长测算

学习率η 也称为步长, 在标准BP算法中定为常数, 然而在实际应用中, 学习率不易选择, 选得太小, 收敛速度太慢; 选得过大, 则有可能修正过大, 导致振荡甚至发散^[9]。对于一个特定的问题也很难确定一个从始至终都适合的最佳学习率, 为了加速收敛过程, 一个较好的方法是自适应改变学习率^[10]。通常调节学习率的准则是:通过检查权值的修正量是否真正降低了误差函数来调节学习率参数, 当误差函数降低时, 则说明所选取的学习率值小了, 可以对其增加学习率; 当误差函数减小非常快时, 学习率保持不变; 而当误差函数不减反增时, 应降低学习率^{[11, 12]}。

由于对学习率的调节不具有精确的数学模型, 因此在此引入模糊控制^[13]算法来调节学习率。设误差e的论域为X, 量化为7个等级, 即:

X={-3, -2, -1, 0, 1, 2, 3}

选取控制量lr的论域为Y, 量化为7个等级, 即:

Y={-3, -2, -1, 0, 1, 2, 3}

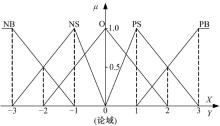
做出语言变量的隶属函数曲线如图2所示。描述输入变量及输出变量的语言值的模糊子集为{负大(NB), 负小(NS), 零(O), 正小(PS), 正大(PB)}。

	Figure Option View Download New Window
	图2 语言变量的隶属函数曲线Fig.2 Language variable membership function curve

由图2可以得到表1模糊变量e及lr的赋值表。经过反复测试调整后得到如表2所示的模糊控制规则。

表1 模糊变量(e, lr)的赋值表 Table 1 Fuzzy variable(e, lr)assignment table

表2 控制规则表 Table 2 Control rules table

解模糊化采用最大隶属度法, 即选取模糊子集中隶属度最大的元素作为控制量, 例如模糊子集为C, 所选择的隶属度最大的元素u^*应满足:

$\begin{matrix} u_{c} (u^{*}) \geq u_{c} (u), u \in U (7) \end{matrix}$

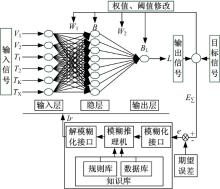
若u^*仅为一个, 则选择该值作为控制量。若u^*有多个, 则选取它们的平均值 $\begin{matrix} {\bar{u}}^{*} \end{matrix}$ 作为控制量。最大隶属度方法简单易行, 算法实时性好^[14]。

建立的基于模糊自适应调节学习率的神经网络模型如图3所示。图3中, L为输出的车长; W₁为输入层到隐含层的权值; W₂为隐含层到输出层的权值; B、B_L为隐含层和输出层的阈值; E_Σ为误差; e为偏差量; lr为学习率。

	Figure Option View Download New Window
	图3 基于模糊自适应调节学习率的 BP神经网络算法模型图Fig.3 Model diagram of BP neural network algorithm based on fuzzy logic adaptive learing rate

3 实验验证及分析

通过Matlab软件内部的神经网络工具箱来对网络进行训练, 把在绿色通道检测现场测得的部分数据作为学习样本数据, 其他的数据作为训练样本数据就可以训练网络, 为了使网络尽快收敛, 所有数据均使用了归一化处理。合理调整网络的学习参数, 经过多次训练达到了目标要求(均方误差在3%以内), 并得到了神经网络模型。神经网络的训练结束后, 即可得到以下各式:

B_L=0.1201;

B= $\begin{matrix} {[\begin{matrix} 0.9910 & - 1.5685 & 1.6639 & 1.6971 & - 0.5662 & - 0.4668 & 1.7756 & 1.0218 \end{matrix}]}^{T} \end{matrix}$ ;

w₂= $\begin{matrix} [\begin{matrix} - 1.5160 & - 1.0431 & 2.0398 & - 0.8998 & 1.6801 & 2.2724 & 1.9053 & - 2.7053 \end{matrix}] \end{matrix}$ ;

w₁= $\begin{matrix} [w_{V_{1}} w_{V_{2}} w_{T_{1}} w_{T_{2}} w_{T_{K}} w_{T_{X}}] \end{matrix}$ =

$\begin{matrix} [\begin{matrix} - 1.8814 & 0.7680 & 1.1561 & - 0.9124 & 1.2409 & - 1.1548 \\ 1.0692 & 0.4208 & 1.2703 & - 0.1200 & - 1.0029 & - 0.5287 \\ - 3.8579 & 1.6697 & - 0.7934 & 1.3051 & 1.3282 & 0.3755 \\ - 0.3549 & - 1.4032 & 0.1433 & 0.1615 & 1.1126 & 2.0731 \\ - 2.5776 & - 0.2750 & 1.5832 & 0.3499 & 0.6262 & - 0.9715 \\ 1.0325 & 1.3766 & 1.0486 & 2.1654 & - 2.1703 & - 0.6534 \\ 0.7795 & - 1.1354 & - 0.3098 & 0.2134 & 1.4335 & - 0.8043 \\ - 0.7901 & 0.9765 & 0.4525 & 1.8531 & - 0.6338 & - 0.3070 \end{matrix}] \end{matrix} \begin{matrix} \begin{matrix} 。 \end{matrix} \end{matrix}$

这样便可以确定六元函数L=f(V₁, V₂, T₁, T₂, T_K, T_X):

L=purelin $\begin{matrix} \{\overset{8}{\sum_{i = 1}} tansig [V_{1} W_{V_{1}} (i) + V_{2} W_{V_{2}} (i) + \end{matrix}$

T₁ $\begin{matrix} W_{T_{1}} \end{matrix} \begin{matrix} (i) \end{matrix}$ +T₂ $\begin{matrix} W_{T_{2}} \end{matrix} \begin{matrix} (i) \end{matrix}$ +T_K $\begin{matrix} W_{T_{K}} \end{matrix} \begin{matrix} (i) \end{matrix}$ +

$\begin{matrix} T_{X} W_{T_{X}} (i) + B (i) W_{L} (i)]\} \end{matrix}$ +B_L

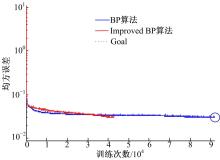
BP算法改进前后的目标训练图如图4所示, 其中蓝色为改进前的目标训练图, 其学习率设置为0.01; 红色为改进后的目标训练图, 采用自适应调节学习率的方法。

	Figure Option View Download New Window
	图4 BP算法改进前后目标训练图Fig.4 BP algorithm improved before and after the target training

图中纵坐标表示每次训练的均方误差, 横坐标表示训练次数。由图中可以看出, 在相同情况下, 改进后的收敛速度明显快于改进前的收敛速度, 改进前需要91 796次训练达到所需的训练精度3%, 而改进后只需要42 751次训练即可达到同样的训练精度。

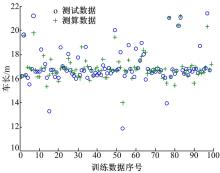
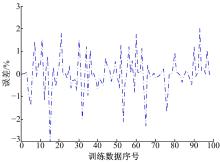
神经网络的测算数据与测试数据的对比图和误差变化如图5和图6所示。由两图对比可以看出, 车长数据大多数分布在16 m到18 m之间, 误差分布在± 1%之间。

	Figure Option View Download New Window
	图5 神经网络测算数据与测试数据的对比Fig.5 Neural network calculation data and test data comparison

	Figure Option View Download New Window
	图6 误差变化Fig.6 Error variation

训练精度为3%时测算结果与实际车长部分数据的比较见表3, 由表3可知, 误差在3%以内。

表3 测算车长与实际车长比较 Table 3 Calculated results compared with the actual length

在不同训练精度下改进前后网络训练次数的对比见表4。由表4可以看出:在训练精度为3%到6%之间, 改进后的训练次数明显少于改进前, 收敛速度加快。

表4 在不同训练精度下算法改进前后网络训练次数对比 Table 4 Comparison of network training times before and after algorithm improvements under different training accuracy

4 结束语

提出了一种基于模糊自适应调节学习率的BP神经网络测算动态行驶车辆车长的方法, 该方法能够在车辆通过绿色通道检测系统的动态过程中精确测算出车辆长度。经过训练好的神经网络测算得到的结果与实际车长进行对比, 误差控制在3%以内, 达到了较好的结果, 证明用神经网络方法可以提高动态车辆车长的测算精度。通过模糊逻辑自适应调节学习率改进BP神经网络后, 收敛速度有了很大提升, 能够有效缩短BP神经网络的训练时间。实验表明, 该方法具有较高的计算精度, 能够达到实际应用的要求。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	张哲, 金兆国, 蔡丽丹, 等. 绿色通道货物检测技术[J]. 吉林交通科技, 2012(1): 43-46. Zhang Zhe, Jing Zhao-guo, Cai Li-dan, et al. Green channel cargo detection technology[J]. Jilin Transportation Technology, 2012(1): 43-46. [本文引用:1]
[2]	段世忠, 袁昊, 王明明, 等. 一种针对金属违禁品的绿色通道敞篷车雷达检测方法[P]. 中国: 201010120124. 5, 2012-07-25. [本文引用:1]
[3]	向长波, 宋明, 宋健中. 光切法测量运动车厢中煤堆的体积[J]. 光学技术, 2009, 35(2): 225-228. Xiang Chang-bo, Song Ming, Song Jian-zhong. Coal volume measuring in mobile carriage with light-sectioning method[J]. Optical Technique, 2009, 35(2): 225-228. [本文引用:1]
[4]	闫霞. 基于机器视觉的体积测量系统研究[D]. 洛阳: 河南科技大学信息工程学院, 2011. Yan Xia. Study of volume measurement system based on machine vision[D]. Luoyang: Information Engineering College, Henan University of Science and Technology, 2011. [本文引用:1]
[5]	李寿涛, 马用学, 郭鹏程, 等. 一种基于有限状态自动机的绿通车辆驾驶室避让控制[J]. 吉林大学学报: 工学版, 2014, 44(4): 1069-1075. Li Shou-tao, Ma Yong-xue, Guo Peng-cheng, et al. Control method for vehicle cab avoidance in free toll lane of highway based on finite state machine[J]. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(4): 1069-1075. [本文引用:2]
[6]	Baldi P, Hornik K. Neural networks and principal component analysis: learning from examples without local minima[J]. Neural Networks, 1989, 2(1): 53-58. [本文引用:1]
[7]	Vogl T P, Mangis J K, Rigler A K, et al. Accelerating the convergence of the back-propagation method[J]. Biol Cybernetics, 1988, 59(4-5): 257-263. [本文引用:1]
[8]	张雨浓, 杨逸文, 李巍. 神经网络权值直接确定法[M]. 广州: 中山大学出版社, 2010. [本文引用:1]
[9]	Mou Rui, Chen Qin-yin, Huang Min-ying. An improve BP network and its application[C]∥2012 Fourth International Conference on Computational and Information Sciences, Kuala Lumpur, Malaysia, 2012: 477-480. [本文引用:1]
[10]	Mo Lian-guang, Xie Zheng. An improved BP neural network based on IPSO and its application[J]. Journal of Computers, 2013, 8(5): 1267-1272. [本文引用:1]
[11]	Fan Tie-hu, Qin Gui-he, Zhao Qi. Research on an improved BP neural network based on fast quantized orthogonal genetic algorithm[C]∥Fifth International Conference on Natural Computation, Tianjin, 2009: 269-273. [本文引用:1]
[12]	Li Xiao-yuan, Qi Bin, Wang Lu. A new improved BP neural network algorithm[C]∥Second International Conference on Intelligent Computation Technology and Automation, Changsha, Hunan, 2009: 19-22. [本文引用:1]
[13]	李士勇. 模糊控制[M]. 哈尔滨: 哈尔滨工业大学出版社, 2011. [本文引用:1]
[14]	李世武, 田晶晶, 沙学锋, 等. 基于模糊综合评价和BP神经网络的车辆危险状态辨识[J]. 吉林大学学报: 工学版, 2011, 41(6): 1609-1613. Li Shi-wu, Tian Jing-jing, Sha Xue-feng, et al. Identification of vehicle risk status based on fuzzy comprehensive evaluation and BP neural network[J]. Journal of Jilin University (Engineering and Technology Edition), 2011, 41(6): 1609-1613. [本文引用:1]

2012

0.0

. 2012, (1):43-46

Green channel cargo detection technology

绿色通道货物检测技术

Zhang Zhe , Jing Zhao-guo , Cai Li-dan

张哲, 金兆国, 蔡丽丹

文章对于目前高速公路绿色通道货车夹带非绿色通道货物的问题进行分析,对比现有检测技术中的几种射线源,将目前绿色通道货物检测方法总结为三种模式:全人工模式、半人工模式、全自动模式,并分别对其所包含的方法进行描述和评价。指出随着科技水平的提高和人们需求的增长,全自动模式将成为绿色通道货物检测的主流。

... 0 引言目前通常采用吨位法^[1]和无损检测法^[2]等技术对过往高速公路绿色通道的车辆进行检测,然而这些方法往往需要对过往车辆或车厢长度进行测量,对于车辆车长的测量,传统方法是进行静态测量,该方法准确度虽然很高,但是达不到实时性要求,同时还存在着很大的缺点,如耗时、需要大量人力、容易造成道路拥堵等,因此需要在货车通过绿色通道检测系统过程中能动态并精确地测算出车辆车长 ...

0.0

2009

0.0

. 2009, 35(2):225-228 DOI:doi:10.3321/j.issn:1002-1582.2009.02.006

Coal volume measuring in mobile carriage with light-sectioning method

光切法测量运动车厢中煤堆的体积

Xiang Chang-bo , Song Ming , Song Jian-zhong.

向长波, 宋明, 宋健中

提出了一种基于光切法实时测量移动车厢中煤堆体积的三维测量方案.采用相邻帧差法实时检测运动车厢的边缘.当车厢前边缘到达检测位置时,开始提取光刀中心获取一系列平行截面的轮廓线;当车厢后边缘到达检测位置时,该节车厢检测完成,然后根据一系列截面轮廓线计算整节车厢的煤堆体积.实验结果表明,所提出的方法具有计算精度高,结构简单,抗光照能力强等特点.

... 目前对运动物体实时测量的方法主要有光切法^[3]和机器视觉法^[4],但由于我国高速公路上行驶的很多车辆都经过改装,车身表面不规则、不平整,使得运用这些方法测量的车长误差较大 ...

2011

0.0

. 2011, :-

Study of volume measurement system based on machine vision

基于机器视觉的体积测量系统研究[D]

Yan Xia.

闫霞

“绿色通道”是国家提出的一项惠民利农的政策,但在政策实施的同时,出现了一些假冒“绿色通道”的车辆,逃避正常规费,搅乱了正常的通行秩序。目前常用的检测方法还是人工检测,既增加了人力成本,又影响了通行效率。这就需要技术手段来完成对通行车辆的检测,完善机电收费系统,这对绿色通道政策的长期实施有重要的现实意义。针对以上需求,本文提出了一种比重法检测系统,该系统是根据货车载重、货物体积和货物密度之间的对比关系,通过计算分析判别所载货物和申报货物之间的相符性。完整的比重法检测系统是由称重检测系统、光电体积测量系统、车牌识别系统三部分组成。而光电体积测量系统是该系统的核心部分,本文将重点讨论光电体积测量系统。随着计算机图像处理和光电技术等相关学科的快速发展,机器视觉测量技术在工业测量中得到了广泛的应用,它是利用CCD摄像机为图像传感器,结合图像处理等技术来完成非接触式测量。光电体积测量系统正是基于机器视觉测量技术设计的,采用了结构光测量的方法,结构光测量方法的基本原理是通过结构光投射器向被测物体的表面投射结构光的图样,然后获得由于物体高度变化而产生的变形图像,从而实现物体的三维轮廓测量。本测量系统是利用安装在车道正上方的摄像机、激光器进行车厢顶面的拍摄和测量;并利用安装在车道侧方的CCD摄像机、激光器配合光电传感器进行车辆长度的测量。通过HALCON软件处理,得到车辆的有效载货体积。本文首先从机器视觉测量系统的基本理论出发,对光电体积测量系统进行了总体的设计。通过对现有的摄像机标定方法进行比较分析,结合现场的实际情况和项目需求提出了本体积测量系统的标定方法—基于HALCON软件的摄像机标定。然后对CCD摄像机拍摄到的激光条纹进行平滑处理、二值化处理、细化处理等,再经过曲线拟合的方法,将其还原到实际的三维测量数据。在分析数学理论的基础上,提出了两种求解不规则图形的截面面积的方法;结合本系统,详细地对车厢长度的测量进行了设计分析。最后分析了体积测量系统的实现,包括硬件安装和软件工作流程,并对现场测试的实验数据以及系统产生的误差进行了分析。绿色通道车辆检测是个复杂过程,需要结合多种手段才能提高检测的精度,比重法检测是绿色通道车辆检测的一部分。光电体积测量系统对车辆检测来说是创新的成果,当前的系统工程化程度还不高,需要积累大量的实验数据,设法从中寻找更具备检测判断作用的统计规律或关系因素,不断改进检测算法以提高其检测精度。

2014

0.0

. 2014, 44(4):1069-1075 DOI:doi:10.13229/j.cnki.jdxbgxb201404026

Control method for vehicle cab avoidance in free toll lane of highway based on finite state machine

一种基于有限状态自动机的绿通车辆驾驶室避让控制

Li Shou-tao , Ma Yong-xue , Guo Peng-cheng

李寿涛, 马用学, 郭鹏程

摘　要：在高速公路绿通车道检测过程中，为了避免射线对驾驶员身体造成伤害，需要对车辆的驾驶室进行避让。本文提出了一种基于有限状态自动机的绿通车辆驾驶室避让控制方法。首先在对车辆通过绿通车道时的状态进行分析的基础上，建立了车辆驾驶室避让的自动状态机模型；然后根据该模型编制了相应的控制程序，对该状态机模型进行了仿真验证和考核；最后对绿通车辆大量的实测数据进行分析。结果表明：基于有限状态自动机的驾驶室避让控制方法能够准确有效地实现驾驶室避让控制，有效地剔除非车辆通行所导致的误动作。

... 本文在绿色通道检测系统^[5]的基础上,通过对大量实测数据的分析,提出一种基于模糊逻辑自适应调节学习率的BP神经网络对动态行驶车辆车长进行测算的方法,最后通过实验验证该方法能够有效地提高测算精度 ...

... 在对驾驶员的驾驶行为进行分析的基础上,对现场大量的绿色通道车辆进行了测试,得知当绿色通道车辆通过检测区域时,车速会在一定范围变化,其变化规律大致如图1中^[5]#cod#x0201c ...

1989

0.0

... 在此,总体误差E被看作是权向量w的函数,即E=E(w)^[6,7] ...

1988

0.0

... 在此,总体误差E被看作是权向量w的函数,即E=E(w)^[6,7] ...

2010

0.0

... )对网络进行训练^[8] ...

2012

0.0

... 选得过大,则有可能修正过大,导致振荡甚至发散^[9] ...

2013

0.0

... 对于一个特定的问题也很难确定一个从始至终都适合的最佳学习率,为了加速收敛过程,一个较好的方法是自适应改变学习率^[10] ...

2009

0.0

... 而当误差函数不减反增时,应降低学习率^[11,12] ...

2009

0.0

... 而当误差函数不减反增时,应降低学习率^[11,12] ...

2011

0.0

. 2011, :-

李士勇

... 由于对学习率的调节不具有精确的数学模型,因此在此引入模糊控制^[13]算法来调节学习率 ...

2011

0.0

. 2011, 41(6):1609-1613

Identification of vehicle risk status based on fuzzy comprehensive evaluation and BP neural network

基于模糊综合评价和BP神经网络的车辆危险状态辨识

Li Shi-wu , Tian Jing-jing , Sha Xue-feng

李世武, 田晶晶, 沙学锋

The weight vector of the evaluation indexes was determined by the fuzzy hierarchy analysis, the membership functions of the evaluation indexes to the evaluation class were established using the ridge function, and a BP neural network model for evaluation of the vehicle safety status was built using the neural network tool box in Matlab software. The experiments were performed using the preset fault test method, the operation parameters of the vehicle under the road test process were acquired by the vehicle monitoring and early-warning system. The training samples for the neural network were obtained by the fuzzy comprehensive evaluation, and the trained BP neural network was used to evaluate the vehicle safety status in the road test. The road test results showed that the neural network evaluation is more sensitive and more accurate than the fuzzy comprehensive evaluation, providing a new method for identification of the vehicle risk status.

考虑驾驶员、车辆、环境和管理因素对车辆安全状态的影响,建立了车辆安全状态评价体系。采用模糊层次分析法确定了各评价指标的权重,利用岭型函数建立了评价指标对评价等级的隶属度函数,在Matlab神经网络工具箱中构建了车辆安全状态神经网络评价模型。采用预设故障的试验方法,利用车辆监测预警系统采集道路试验过程中车辆的运行状态参数。通过模糊综合评价得出神经网络所需的训练样本,运用训练好的BP神经网络对道路试验中车辆安全状态进行评价。道路试验结果表明：神经网络评价较模糊综合评价灵敏度更高、更准确,为车辆危险状态辨识提供了一种新方法。

... 最大隶属度方法简单易行,算法实时性好^[14] ...