加入虚拟标签的射频识别室内定位算法

引用本文

陈增强, 国峰, 牛攀峰, 张青. 加入虚拟标签的射频识别室内定位算法. 2015, 45(6): 1887-1894
CHEN Zeng-qiang, GUO Feng, NIU Pan-feng, ZHANG Qing. Radio frequency identification indoor location algorithm with virtual tags. Journal of Jilin University Engineering and Technology Edition, 2015, 45(6): 1887-1894 复制到剪切板

Permissions

加入虚拟标签的射频识别室内定位算法

陈增强^1,^2,³, 国峰^1,², 牛攀峰^1,², 张青³

1.南开大学计算机与控制工程学院,天津 300071

2.南开大学天津市智能机器人技术重点实验室, 天津 300071

3.中国民航大学理学院,天津 300300

作者简介:陈增强(1964-),男,教授,博士生导师.研究方向:智能预测控制,智能物联系统,多智能体系统控制.E-mail:chenzq@nankai.edu.cn

基金:国家自然科学基金项目(61174094); 天津市自然科学基金项目(14JCYBJC18700,13JCYBJC17400)

摘要

在路标(LANDMARC)定位算法的基础上,提出把多个参考标签作为一个整体来与待定位标签比较RSSI值,先找出待定位标签所在的区域范围,并在此区域范围内线性添加一些虚拟参考标签,最后通过加权估计来确定待定位标签的位置坐标。仿真实验和硬件测试结果表明:改进后的算法在没有增加任何硬件成本的同时,具有更好的稳定性和抗干扰性,并且定位精度也有显著提高,更适用于室内定位。

关键词: 计算机应用; 无源射频识别; 定位系统; 路标算法; 参考标签; 虚拟标签

中图分类号:TN911.23 文献标志码:A 文章编号:1671-5497(2015)06-1887-08

Radio frequency identification indoor location algorithm with virtual tags

CHEN Zeng-qiang^1,^2,³, GUO Feng^1,², NIU Pan-feng^1,², ZHANG Qing³

1.College of Computer & Control Engineering, Nankai University, Tianjin, 300071, China

2.Tianjin Key Laboratory of Intelligent Robotics, Nankai University, Tianjin, 300071, China

3.College of Science, Civil Aviation University of China, Tianjin 300300, China

Abstract

This paper proposes a method to compare the Received Signal Strength Indicator (RSSI) of target tag with the RSSI of reference tags while taking many reference tags as a whole. First, this method figures out the area of target tag; then adds virtual reference tags in this area; and finally determines the position of target tag via weighted estimate. The simulation and hardware experiments demonstrate that the improved algorithm has better stability and stronger anti-interference without increasing any physical cost. Besides, the location accuracy is enhanced obviously, thus the algorithm is more applicable to indoor location system.

Keyword: computer application; passive radio frequency identification; location system; LANDMARC algorithm; reference tag; virtual tag

Show Figures

0 引言

射频识别(Radio frequency identification, RFID)技术是一种利用射频通信实现的非接触式自动识别技术^[1]。目前已广泛应用于物流和工业制造等领域^{[2, 3]}。

近年来随着RFID产业的兴起, 将其应用到定位服务中也受到了越来越多的关注。但是现在绝大多数的RFID定位都是区域性的、范围性的定位服务^[4], 不能得到非常精确的位置结果。目前, 基于卫星通信和移动网络通信的定位技术已经非常成熟, 但是这些都是应用于室外的定位技术。由于室外大型障碍物反射信号所引起的多径传播效应, 使其难以应用到室内定位^[5]。因为RFID非视距、高灵敏度、低成本和可以同时识别多个目标的特点, 使其更适用于室内定位领域。然而室内不同于室外, 由于室内环境摆设复杂、精密度要求较高, 所以操作起来也相对困难很多。将RFID技术应用到室内定位仍有诸多问题需要解决。RFID定位主要基于3种原理^[6]:接收信号角度(Angle of arrival, AOA)、接收信号时间(Time of arrival, TOA)和接收信号场强(Received signal strength indication, RSSI)。利用AOA^[7]和TOA^[8]定位的成本较高, 所以绝大多数的RFID定位系统都是基于RSSI的。研究者们提出的比较著名的RFID定位系统有SpotOn系统, BlueBot系统, LANDMARC系统等。SpotOn系统^[9]采用的是网络分布式硬件基础结构, 根据Ad hoc时间延迟法进行定位, 其定位精度直接被网络群组大小所限制, 而且精度不及信号传播时延法。BlueBot系统^[10]使用了一种无人操作的机器人, 这种机器人自身安装有一个Wi-Fi定位终端和一个RFID读写器, 机器人在室内移动扫描标签并确定标签的位置, 实现起来相对复杂而且成本较高。LANDMARC系统^[11]采用的是最近邻居算法, 它在室内环境中布置一定数目位置的参考标签作为定位基准, 根据待定位标签与参考标签的RSSI相似程度来确定待定位标签的位置, 成本较低, 而且较容易实现。

本文主要致力于改进LANDMARC算法, 并提高它的定位精度, 文献[12]为此奠定了良好的基础。

1 相关工作

本文主要讨论的是基于无源RFID室内定位系统, 定位的目标是无源RFID标签, 其本身没有任何电源供电, 它只能从读写器天线发出的射频电磁波中提取其工作所需的能量。无源RFDI标签一般均采用反射调制方式完成RFID标签信息向读写器的传送。

室内RFID的信号传播模型一般为对数距离损耗模型^[13]:

$\begin{matrix} PL (d) = PL (d_{0}) + 10 nlo g_{10} (\frac{d}{d_{0}}) + X_{σ} (dB) (1) \end{matrix}$

式中:PL(d)为空间中传输距离为d的路径损耗; d₀为参考距离, 通常为1 m; n为路径损耗指数, 依赖于周围环境和建筑物类型; X_σ是均值为0、方差为σ ²(dB)的高斯随机变量, X_σ又被称为阴影衰落, 用来描述多径衰落、障碍物、标签方向性和移动物体等环境因素引起的室内无线信号传播的随机衰落。

令P_r(d)为接收器与发射器距离为d时的接收器接收到的信号强度(RSSI); P_t为发射器的发射信号强度, 则可以得出:

$\begin{matrix} P_{r} (d) = P_{t} - PL (d_{0}) - 10 nlo g_{10} (\frac{d}{d_{0}}) + X_{σ} (dB) (2) \end{matrix}$

上面所述的传播模型是针对某些环境而得出的, 在实际的工作中预测值的误差可能会比较大, 需要不断地调整, 本文主要采用该模型在仿真实验中模拟RFID的传播信号。

2 LANDMARC定位算法

2.1 算法原理

LANDMARC算法是根据参考标签来进行辅助定位的, 参考标签充当系统的定位参考点。这种方法最初是基于有源RFID系统的, 但其在无源RFID系统中也具有很好的适用性。其核心思想是找到与待定位标签RSSI相似的参考标签, 并根据已知的参考标签位置加权估计待定位标签的位置。

假设系统中有M个读写器和N个参考标签。

(1)对于第i个参考标签, 其位置为(x_i, y_i)(i=1, 2, 3, …, N); 其对应的信号强度为P_i=(P_i_{, 1}, P_i_{, 2}, P_i_{, 3}, …, P_i_,_M), 其中P_i_,_j(i=1, 2, …, N; j=1, 2, …, M)表示第j个读写器读出的第i个参考标签的信号强度。

对于待定位标签, 其对应的信号强度为S=(S₁, S₂, S₃, …, S_M), 其中S_j(j=1, 2, …, M)表示第j个读写器读出的待定位标签的信号强度。

(2)定义第i个参考标签与待定位标签的紧邻程度为:

$\begin{matrix} \begin{matrix} E_{i} = | S - P_{i} |= \\ \sqrt{(S_{1} - P_{i, 1})^{2} + (S_{2} - P_{i, 2})^{2} + \dots + (S_{M} - P_{i, M})^{2}} (3) \end{matrix} \end{matrix}$

E_i越小表示待定位标签与参考标签的信号强度越相似, 其距离参考标签的位置也越近。

(3)选取k个最紧邻参考标签(E_i最小的k个参考标签), 位置分别记为( $\begin{matrix} {\tilde{x}}_{i} \end{matrix}$ , $\begin{matrix} {\tilde{y}}_{i} \end{matrix}$ )(i=1, 2, …, k), 与待定位标签的紧邻度用 $\begin{matrix} {\tilde{E}}_{i} \end{matrix}$ (i=1, 2, …, k)表示。

定义权重系数为:

$\begin{matrix} W_{i} = \frac{1}{{\tilde{E}}_{i}^{2}} / \overset{k}{\sum_{j = 1}} (\frac{1}{{\tilde{E}}_{j}^{2}}) (4) \end{matrix}$

则待定位标签的位置坐标( $\begin{matrix} {\bar{x}}_{0} \end{matrix}$ , $\begin{matrix} {\bar{y}}_{0} \end{matrix}$ )可用如下公式表示:

$\begin{matrix} ({\bar{x}}_{0}, {\bar{y}}_{0}) = \overset{k}{\sum_{i = 1}} (W_{i} \cdot ({\tilde{x}}_{i}, {\tilde{y}}_{i})) (5) \end{matrix}$

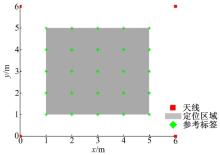
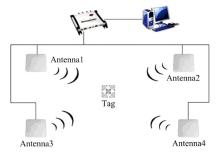
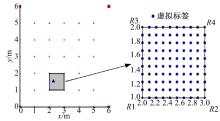
此时, 待定位标签的估计位置与实际位置的误差值为:e= $\begin{matrix} \sqrt{{({\bar{x}}_{0} - x_{0})}^{2} + {({\bar{y}}_{0} - y_{0})}^{2}} \end{matrix}$ , 其中(x₀, y₀)为待定位标签的实际位置坐标。

2.2 算法仿真实验

(1)模拟一个6 m× 6 m的正方形区域, 在这个区域内布置4个读写器天线(高度为1 m), 25个无源参考标签(高度为0 m), 其定位区域示意图如图1所示。该环境中, 有效的定位区域为4 m× 4 m, 图1中灰色部分所示。

	Figure Option View Download New Window
	图1 仿真环境的布置Fig.1 Layout of simulation environment

设4个读写器天线的发射功率全部为P_t=40 dBm, 传播模型采用对数距离损耗模型, 参数分别选择n=2.4; d₀=1 m; PL(d₀)=30 dBm; X_σ~N(0, 0.25)。则系统中(x, y)处的信号强度为:

$\begin{matrix} P_{r} (x, y) = \overset{4}{\sum_{i = 1}} \{10 - 24 \lg d_{i} + N (0, 0.25)\} (6) \end{matrix}$

式中:d_i(i=1, 2, 3, 4)为(x, y)分别到4个读写器天线的直线距离。

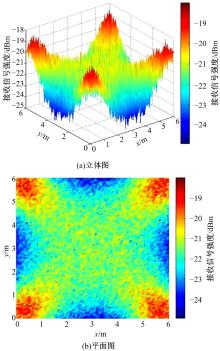
仿真得到该区域内的信号强度分布图如图2所示。

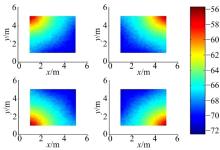
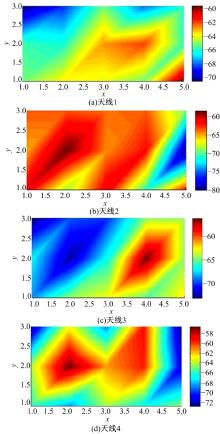
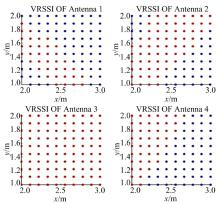
	Figure Option View Download New Window
	图2 定位区域内的信号强度分布图Fig.2 Distribution map of signal stress in location area

(2)无源RFID标签工作所需的能量是从读写器天线发射的电磁波中获得的, 当标签距离读写器天线越近时, 获取的工作能量也越高。仿真时假设标签只能放置在有效定位区域内(高度为0 m), 且标签能够完全无损耗地获取读写器天线传播到标签处的电磁波能量。标签的电磁波传播模型也采用对数距离损耗模型, 其模型参数设置和读写器天线的一样, 于是, 可以计算得到标签传给读写器天线的信号强度值。图3为四个读写器天线接收到的(x, y)处标签信号强度分布图。

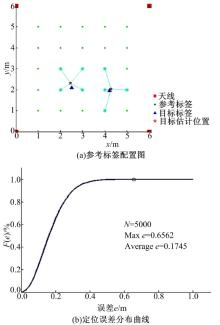
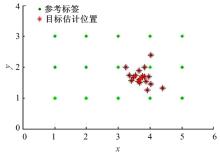
	Figure Option View Download New Window
	图3 仿真中天线的RSSI分布图Fig.3 Antenna’ s RSSI distribution map in simulation

根据LANDMARC定位算法原理, 对待定位标签进行定位, 仿真时选取的最近邻参考标签数目k=4, 定位的效果图如图4(a)所示。

	Figure Option View Download New Window
	图4 LANDMARC定位算法Fig.4 LANDMARC localization algorithm

在待定位区域内随机生成5000个待定位标签, 其定位结果的累计误差分布曲线如图4(b)所示, 其中e为定位误差; F(e)为误差分布, 最大误差为0.6562 m, 平均误差为0.1745 m。前文已经提到, LANDMARC这种算法本身就是一种近似的估计, 即使信号在传播过程中没有受到任何的干扰, 也存在一定的定位误差。仿真中, 如果令X_σ~N(0, 0), 即去掉信号传播过程中的干扰量, 系统的平均定位误差大概也在0.1 m左右。

2.3 硬件实验测试

搭建无源RFID定位系统的硬件平台, 图5为其结构图。其中, 读写器采用的是Impinj公司生产的超高频Speedway Revolution R420读写器, 具有4个收发一体的RP TNC天线接口; 天线采用的是莱尔德科技公司设计的A9028L30NF圆极化平板天线, 共4个; RFID标签采用的是Impinj配套的H47+Monza 4E Dry Inlay全向性无源RFID标签。整个系统的工作频率为902~908 MHz, 最大接收灵敏度为-82 dBm。

	Figure Option View Download New Window
	图5 硬件平台结构图Fig.5 Structure of hardware platform

平台的软件部分由C#.NET和Matlab组成。其中C#.NET主要用来完成对各种实时数据的采集, 包括各个标签的EPC、RSSI值、读取次数、读取时间等。Matlab主要用来实现定位算法的计算和各种实验数据的实时分析。它们之间通过调用Matlab Application Type Library这个com组件来进行数据的交互。这种结构非常有利于定位算法的修改和实时数据的分析。

在读取标签RSSI值时, 由于干扰因素的存在, 需要多次读取同一个标签的RSSI值, 然后取平均, 值得注意的是每一个标签的读取次数是不一样的, 必须分别记录。在实验中可能存在由于标签碰撞、标签摆放位置等原因造成天线的漏读, 实验中把这些漏读的标签RSSI值设为-100 dBm, 防止运算中出现极值。

实验中, 布置三排五列共15个参考标签, 布置1个待定位标签。

待定位标签的位置坐标为(3.75, 1.75), 这里的每“ 1” 个单位代表的是图6中小正方形的边长50 cm。进行20次的定位计算, 得到其平均定位误差为0.3506, 即17.53 cm。

	Figure Option View Download New Window
	图6 硬件实验结果Fig.6 Experimental result of hardware platform

从图6可以看出, 待定位标签的估计位置都在实际位置附近, 但是误差还是很大, 最大误差可达0.77(38.5 cm)。误差大的主要原因是环境中的干扰因素太多。图7为4个天线根据参考标签RSSI值画出的RSSI分布图, 可以清楚地看出, 其信号强度分布相比仿真环境(见图3)来说变化极其不规律, 这也给定位造成了很大影响。但是总体来说, LANDMARC定位算法的稳定性还是很高, 相比其他算法, 它能准确地把目标定位在一定的区域范围内, 并且在整个算法过程中, 它无需知道读写器天线的位置坐标, 无需求解标签到读写器天线的实际距离, 实现起来非常快捷、方便。

	Figure Option View Download New Window
	图7 实际环境中的RSSI分布图Fig.7 RSSI distribution map in actual environment

影响LANDMARC算法定位精度的因素还有很多, 例如参考标签的布局(参考标签可以布置成正方形也可布置成三角形)、参考标签的布置密集程度、最近邻参考标签数目k的选择以及权重函数的定义也是需要考虑的因素。总结LANDMARC算法的优点如下:①定位结果比较稳定, 具有非常强的抗干扰性; ②采用增加参考标签的方法来提高定位精度, 降低了成本。其缺点如下:①其定位原理只是一种近似的估计, 不可能得到非常准确的结果, 存在一定的定位误差; ②定位精度过度依赖于参考标签的密集程度。参考标签布局越密集, 定位精度也越高, 但布局太密集的话, 多径效应会给定位精度带来一定的影响; ③权重系数W_i和最近邻参考标签个数k的定义具有一定的经验性, 并且不具备普遍适用性, 不同的环境需要不同的权重系数。

3 改进的LANDMARC算法

3.1 算法原理及仿真

在进行LANDMRAC算法的硬件实验时, 分析待定位标签选中的最近邻参考标签, 会经常出现图8中所示的情况。很显然, 这样的定位结果即使是比较接近真实值, 但也是不可取的。根据算法原理, 被选中的4个参考标签应该是聚集在一块儿的, 最理想的结果就是4个参考标签能正好连成一个正方形, 而图8中的4个参考标签明显比较分散, 对定位性能的影响是非常大的, 这种现象产生的原因是实际环境中的干扰太大, 造成信号强度的分布极不规律。为了避免出现这种现象, 本文对LANDMARC算法改进如下:在选取最近邻参考标签时, 把4个能连成正方形的参考标签目标块作为一个整体来考虑。

	Figure Option View Download New Window
	图8 硬件平台上LANDMARC定位示意图Fig.8 Sketch map of LANDMARC in hardware platform

选取最小的 $\begin{matrix} \bar{E} \end{matrix}$ = $\begin{matrix} \overset{4}{\sum_{i = 1}} \end{matrix} \begin{matrix} {\tilde{E}}_{i} \end{matrix}$ , 其中 $\begin{matrix} {\tilde{E}}_{i} \end{matrix}$ (i=1, 2, 3, 4)对应的点必须能够连成一个边长为1 m的正方形的目标块, 最后根据 $\begin{matrix} {\tilde{E}}_{i} \end{matrix}$ (i=1, 2, 3, 4)来计算待定位标签的位置。这样选出的4个参考标签就能保证连成封闭的最小区域, 算法的抗干扰能力也将增强。

同时, 在选中目标块的基础上, 再在目标块内加入虚拟的参考标签提升定位精度。以上面提到的仿真为例, 先搜索到待定位标签所在的正方形目标块区域, 再在这个区域内添加96个虚拟标签, 形成一个10× 10的标签矩阵。如图9所示, 图中待定位标签的位置是随机生成的, 其坐标是(2.2724, 1.5352)。加入的虚拟标签RSSI值是根据4个参考标签线性插入:

$\begin{matrix} \begin{matrix} RSS I_{(i, j), k} = (P_{R 1, k} + (i - 1) \frac{P_{R 3, k} - P_{R 1, k}}{9}) + \\ (j - 1) (P_{R 2, k} + (i - 1) \frac{P_{R 4, k} - P_{R 2, k}}{9}) / 9 - \\ (P_{R 1, k} + (i - 1) \frac{P_{R 3, k} - P_{R 1, k}}{9}) / 9 (7) \end{matrix} \end{matrix}$

式中:RSSI₍_i_,_j_),_k(i=1, 2, …, 10, j=1, 2, …, 10, k=1, 2, 3, 4)表示第k个天线读到的第i行、第j列的虚拟标签RSSI值。

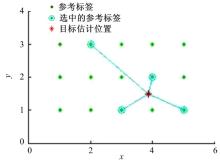
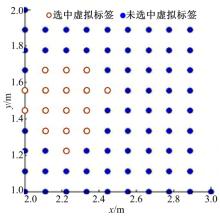
	Figure Option View Download New Window
	图9 添加虚拟标签Fig.9 Add virtual tags

依此类推, 根据4个天线接收到的RSSI值, 可以得到4组对应的虚拟标签RSSI矩阵。再拿待定位标签的RSSI值S=(S₁, S₂, S₃, S₄)分别与对应的虚拟标签RSSI矩阵比较。这里首先定义一个阈值, 待定位标签与虚拟标签的RSSI绝对差值小于这个阈值时, 选中这个虚拟标签作为定位的参考标签; 反之抛弃它。4个天线可以得到4组不同的结果, 如图10所示(仿真中, 阈值设为1); 最终得到被4个天线都选中的虚拟标签, 如图11所示。

	Figure Option View Download New Window
	图10 每个天线选中的虚拟标签Fig.10 Selected virtual tags of each antenna

	Figure Option View Download New Window
	图11 最终选中的虚拟标签Fig.11 Selected virtual tags finally

下面定义求解待定位标签的权重系数, 考虑两个权重系数^[12]:W_i₁表示选中的虚拟标签与待定位标签的接近程度, RSSI值越接近, 其权值越大; W_i₂表示选中的虚拟标签聚集程度, 聚集在一块的虚拟标签越多, 其权值也越大。W_i₁和W_i₂的表达式分别为:

$\begin{matrix} \begin{matrix} W_{i 1} = 1 - \overset{K}{\sum_{k = 1}} \frac{|RSS I_{i, k} - S_{k}|}{K \cdot RSS I_{i, k}} (8) \\ W_{i 2} = \frac{n_{ic}}{\overset{N}{\sum_{i = 1}} n_{ic}} (9) \end{matrix} \end{matrix}$

式中:RSSI_i_,_k为第k个天线读到的第i个虚拟标签RSSI值; S_k为第k个天线读到的待定位标签RSSI值; K为天线的个数; N为最终选中的虚拟标签个数; n_ic为选中的第i个虚拟标签与其他选中的虚拟标签连在一起的个数。

则最终的权重系数为:

$\begin{matrix} W_{i} = W_{i 1} \cdot W_{i 2} (10) \end{matrix}$

最终的待定位标签的估计位置为:

$\begin{matrix} ({\bar{x}}_{0}, {\bar{y}}_{0}) = \overset{k}{\sum_{i = 1}} (W_{i} \cdot ({\tilde{x}}_{i}, {\tilde{y}}_{i})) (11) \end{matrix}$

式中:( $\begin{matrix} {\tilde{x}}_{i} \end{matrix}$ , $\begin{matrix} {\tilde{y}}_{i} \end{matrix}$ )为选中的虚拟标签的位置坐标。

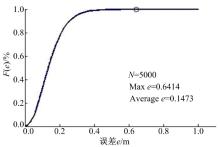
在仿真环境中, 随机生成5000个待定位标签进行试验, 其定位结果的累计误差分布曲线如图12所示, 其中最大定位误差为0.6414 m, 平均定位误差为0.1473 m。定位结果明显优于未改进前的算法。

	Figure Option View Download New Window
	图12 改进后算法的定位误差累计分布图Fig.12 CDF of improved locational algorithm

3.2 硬件实验测试

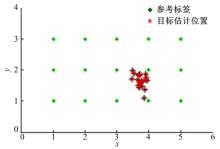
在搭建的硬件实验平台上进行测试, 待定位目标标签的位置坐标仍然设置为(3.75, 1.75), 选择虚拟标签的阈值为3.5 dBm, 连续进行20次的定位实验, 目标点的定位结果如图13所示。

	Figure Option View Download New Window
	图13 改进后算法的定位结果Fig.13 Experimental result of improved algorithm

所有待定位标签的估计位置都分布在(3, 1)、(4, 1)、(4, 2)、(3, 2)标签围成的正方形右上区域, 平均误差为0.2663(13.32 cm), 最大误差为0.6676(33.38 cm)。实验结果表明, 改进的算法比原来的算法具有更强的抗干扰性, 定位精度也提高了将近25%。并且在增加精度的同时, 并没有增加任何的硬件成本。

在改进的算法中有两点需要注意:①本文采用虚拟标签RSSI的插值方法, 属于线性插值方法, 但也可以根据实际环境采用其他的插值方法; ②阈值的选择大小要适中, 太大会选中正方形区域内的所有虚拟标签, 太小则一个虚拟标签也不会选中, 都会影响到定位的精度, 这个阈值要根据实际环境做不同的调整。

4 结束语

对LANDMARC定位算法进行了改进。首先采用将4个参考标签作为一个整体目标块的方式与待定位标签的RSSI值比较, 提高了系统的抗干扰能力。同时在选中的正方形区域内加入虚拟的参考标签来辅助定位。无论是仿真实验还是硬件测试都表明:改进后的算法具有更高的定位精度, 而且没有增加任何硬件成本, 适合室内定位。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	王文峰, 耿力. 基于射频识别的实时定位系统技术研究[J]. 信息技术与标准化, 2007(7): 21-24. Wang Wen-feng, Geng Li. Research on real time locating system technology based on RFID[J]. Tracks for Stand ard & Technology, 2007(7): 21-24. [本文引用:1]
[2]	李敏波, 金祖旭, 陈晨. 射频识别在物流跟踪与追溯系统中的应用[J]. 计算机集成制造系统, 2010, 16(1): 202-208. Li Min-bo, Jin Zu-xu, Chen Chen. Application of RFID on products tracking and tracing system[J]. Computer Integrated Manufacturing Systems, 2010, 16(1): 202-208. [本文引用:1]
[3]	臧传真, 范玉顺. 基于智能物件的制造企业复杂事件处理研究[J]. 计算机集成制造系统, 2007, 13(11): 2243-2253. Zang Chuan-zhen, Fan Yu-shun. Complex event processing of manufacturing enterprises based on smartItems[J]. Computer Integrated Manufacturing Systems, 2007, 13(11): 2243-2253. [本文引用:1]
[4]	黄刚, 钟小勇, 龙渊铭, 等. 基于数据云服务与应用云分离模式的制造资源云定位服务平台[J]. 计算机集成制造系统, 2011, 17(3): 520-524. Huang Gang, Zhong Xiao-yong, Long Yuan-ming, et al. Manufacturing resources cloud locating services platform based on separated data cloud and application cloud[J]. Computer Integrated Manufacturing Systems, 2011, 17(3): 520-524. [本文引用:1]
[5]	Headley W C, da Silva C R C M, Buehrer R M. Indoor location positioning of non-active objects using ultra-wideband radios[C]∥2007 IEEE Radio and Wireless Symposium, Long Beach, CA, USA, 2007: 105-108. [本文引用:1]
[6]	王远哲, 毛陆虹, 刘辉, 等. 基于参考标签的射频识别定位算法研究与应用[J]. 通信学报, 2010, 31(2): 2076-2081. Wang Yuan-zhe, Mao Lu-hong, Liu Hui, et al. Research and application of RFID location algorithm based on reference tags[J]. Journal on Communications, 2010, 31(2): 2076-2081. [本文引用:1]
[7]	Zhou Jun-ru, Zhang Hong-jian, Mo Ling-fei. Two-dimension localization of passive RFID tags using AOA estimation[C]∥2011 IEEE Instrumentation and Measurement Technology Conference, Binjiang, 2011: 1-5. [本文引用:1]
[8]	Ai Zhong-jin, Liu Ye. Research on the TDOA measurement of active RFID real time location system[C]∥3rd IEEE International Conference on Computer Science and Information Technology, Chengdu, China, 2010: 410-412. [本文引用:1]
[9]	Hightower J, Want R, Borriello G. SpotON: an indoor 3D location sensing technology based on RF signal strength[R]. Technical Report UW CSE, University of Washington, Seattle WA, 2000: 1-16. [本文引用:1]
[10]	Montemerlo M, Thrun S, Koller D, et al. FastSLAM: a factored solution to the simultaneous localization and mapping problem[C]∥In Proceedings of the AAAI National Conference on Artificial Intelligence, Edmonton, Canada, 2002: 593-598. [本文引用:1]
[11]	Ni L M, Liu Y H, Lau Y C, et al. LANDMARC: indoor location sensing using active RFID[C]∥Proceedings of the First IEEE International Conference, Fort Worth, 2003: 407-415. [本文引用:1]
[12]	Zhao Y Y, Liu Y H, Ni L M. VIRE: active RFID-based localization using virtual reference elimination[C]∥IEEE International Conference on Parallel Processing, Xi'an, China, 2007: 56-64. [本文引用:1]
[13]	Niu Pan-feng, Chen Zeng-qiang, Li Yi-bo, et al. Location based on passive RFID by using least squares SVM[C]∥Asia Simulation Conference & the International Conference on System Simulation and Scientific Computing, Shanghai, China, 2012: 265-274. [本文引用:1]

2007

0.0

. 2007, (7):21-24 DOI:doi:10.3969/j.issn.1671-539X.2007.07.008

Research on real time locating system technology based on RFID

基于射频识别的实时定位系统技术研究

Wang Wen-feng , Geng Li.

王文峰, 耿力

介绍了基于射频识别技术和定位技术的实时定位系统,阐述了实时定位系统的分类、评估方法和实时定位系统技术的标准制定情况,并提出了相关建议。

... 0 引言射频识别(Radio frequency identification,RFID)技术是一种利用射频通信实现的非接触式自动识别技术^[1] ...

2010

0.0

... 目前已广泛应用于物流和工业制造等领域^[2,3] ...

2007

0.0

. 2007, 13(11):2243-2253 DOI:doi:10.3969/j.issn.1006-5911.2007.11.026

Complex event processing of manufacturing enterprises based on smartItems

基于智能物件的制造企业复杂事件处理研究

Zang Chuan-zhen , Fan Yu-shun.

臧传真, 范玉顺

定义了复杂事件的语法语义和操作符,给出系统体系结构,详细论述了其数据结构.提出共享池的方法来提高检测效率,实现递增检测和共享检测的结果;使用人工时间事件主动检测非自然事件.在此基础上提出利用操作符语义关系,以及约束下移的优化策略.最后给出了综合的复合事件检测算法.仿真试验证明该方法具有较好的效果,应用案例说明该方法具有较好的可用性.

... 目前已广泛应用于物流和工业制造等领域^[2,3] ...

2011

0.0

. 2011, 17(3):520-524

Manufacturing resources cloud locating services platform based on separated data cloud and application cloud

基于数据云服务与应用云分离模式的制造资源云定位服务平台

Huang Gang , Zhong Xiao-yong , Long Yuan-ming

黄刚, 钟小勇, 龙渊铭

为了实现各参与方的业务功能解耦,给出了一类涉及服务需求方、制造服务提供方、制造应用提供方、服务平台运营方四种角色的云制造服务模式.该模式进一步将制造应用提供方细分为解决方案集成方、应用上具开发方、基础数据提供方等角色实现了数据云与应用的分离.着重研究了其中的基础数据提供方,探讨了一种基于制造资源定位技术的制造资源基础数据云平台及其组成,讨论了云定位技术在制造环境下的若干应用场景.最后给出了一种基础数据云与应用云分离的云制造服务框架,为构建云制造服务的实际应用模式提供了新的思路.

... 但是现在绝大多数的RFID定位都是区域性的、范围性的定位服务^[4],不能得到非常精确的位置结果 ...

2007

0.0

... 由于室外大型障碍物反射信号所引起的多径传播效应,使其难以应用到室内定位^[5] ...

2010

0.0

. 2010, 31(2):2076-2081

Research and application of RFID location algorithm based on reference tags

基于参考标签的射频识别定位算法研究与应用

Wang Yuan-zhe , Mao Lu-hong , Liu Hui

王远哲, 毛陆虹, 刘辉

摘　要：对基于参考标签的最近邻居定位算法提出了若干改进,提出了动态k值设定的方法,参考标签可信度的概念和最近邻标签偏差校正算法,并采用了目标标签历史轨迹算法。基于多天线的时分复用搭建了室内定位系统,并且依据改进后的算法开发了相应的界面软件。实测表明改进算法的定位精度和在恶劣环境下定位结果的稳定度比原算法有了明显提高。

... RFID定位主要基于3种原理^[6]:接收信号角度(Angle of arrival,AOA)、接收信号时间(Time of arrival,TOA)和接收信号场强(Received signal strength indication,RSSI) ...

2011

0.0

... 利用AOA^[7]和TOA^[8]定位的成本较高,所以绝大多数的RFID定位系统都是基于RSSI的 ...

2010

0.0

... 利用AOA^[7]和TOA^[8]定位的成本较高,所以绝大多数的RFID定位系统都是基于RSSI的 ...

2000

0.0

... SpotOn系统^[9]采用的是网络分布式硬件基础结构,根据Ad hoc时间延迟法进行定位,其定位精度直接被网络群组大小所限制,而且精度不及信号传播时延法 ...

2002

0.0

... BlueBot系统^[10]使用了一种无人操作的机器人,这种机器人自身安装有一个Wi-Fi定位终端和一个RFID读写器,机器人在室内移动扫描标签并确定标签的位置,实现起来相对复杂而且成本较高 ...

2003

0.0

... LANDMARC系统^[11]采用的是最近邻居算法,它在室内环境中布置一定数目位置的参考标签作为定位基准,根据待定位标签与参考标签的RSSI相似程度来确定待定位标签的位置,成本较低,而且较容易实现 ...

2007

0.0

... 下面定义求解待定位标签的权重系数,考虑两个权重系数^[12]:W_i₁表示选中的虚拟标签与待定位标签的接近程度,RSSI值越接近,其权值越大 ...

2012

0.0

... 室内RFID的信号传播模型一般为对数距离损耗模型^[13]: ...