离散事件触发非线性网络化控制系统鲁棒容错控制

引用本文

曹慧超, 李炜. 离散事件触发非线性网络化控制系统鲁棒容错控制. 2015, 45(6): 1895-1905
CAO Hui-chao, LI Wei. Robust fault-tolerant control for nonlinear networked control system under discrete event-triggered communication scheme. Journal of Jilin University Engineering and Technology Edition, 2015, 45(6): 1895-1905 复制到剪切板

Permissions

离散事件触发非线性网络化控制系统鲁棒容错控制

曹慧超, 李炜

兰州理工大学电气工程与信息工程学院,兰州 730050

李炜(1963-),女,教授,博士生导师.研究方向:动态系统故障诊断与容错控制,工业过程先进控制.E-mail:liwei@lut.cn

作者简介:曹慧超(1986-),女,博士研究生.研究方向:故障诊断与容错控制.E-mail:cchhcc_love@126.com

基金:国家自然科学基金项目(61364011); 甘肃省自然科学基金项目(1308RJZA148); 兰州理工大学基金项目(03-0099)

摘要

首先建立了集网络时变时延、执行器饱和约束及故障、离散事件触发条件于一体的不确定非线性闭环故障网络化控制系统(NCS)模型。然后应用Lyapunov稳定性理论和时延分段技术,结合改进的Jensen积分不等式和互反凸组合引理,推证出了闭环故障NCS稳定的时滞且事件依赖不变集充分条件,并给出了鲁棒容错控制器与离散事件触发条件权矩阵的协同设计方法。最后,通过一个仿真算例验证了本文方法不仅能使基于离散事件触发通信机制(DETCS)的NCS对故障有效容错,而且可通过触发参数的适当选取来节省有限的网络资源。

关键词: 计算机应用; 容错控制; 离散事件触发; 网络化控制系统; 执行器饱和; 执行器故障

中图分类号:TP302.8 文献标志码:A 文章编号:1671-5497(2015)06-1895-11

Robust fault-tolerant control for nonlinear networked control system under discrete event-triggered communication scheme

CAO Hui-chao, LI Wei

College of Electrical and Information Engineering, Lanzhou University of Technology, Lanzhou 730050, China

Abstract

First, a new model of uncertain nonlinear closed-loop fault Networked Control System(NCS) is established, which integrates the network time-varying delay, actuator saturation and fault, and the discrete event-triggered condition in a unified framework. Then, utilizing the Lyapunov stability theory and delay decomposition technology, combing the improved Jensen integral inequality and the reciprocal convex combination lemma, the delay- and event-dependent invariant set condition for ensuring closed-loop fault NCS stability is derived. The co-design method for both robust fault-tolerant controller and the weight matrix of discrete event-triggered conditions is given. Finally,a simulation case is employed to demonstrate that the proposed method, which guarantees faulty NCS based on Discrete Event-Triggered Communication Scheme(DETCS), possesses good fault-tolerant performance, and saves the limited network resources by reasonably choosing the triggering parameters.

Keyword: computer application; fault-tolerant control; discrete event-triggered; networked control system; actuator saturation; actuator fault

Show Figures

0 引言

目前, 针对数据通过网络传输时产生的时延、丢包、乱序等影响系统性能的问题, 已在网络化控制系统(Networked control system, NCS)稳定性分析和控制器设计等方面开展了大量的研究工作^{[1, 2, 3, 4]}。同时, 由于NCS结构更分散且复杂化程度甚高, 也就面临了更多的不确定性及更高的系统元部件故障几率, 因此, 为了提高系统安全性和可靠性, 通过对NCS进行容错设计使其对故障不敏感的研究也受到了学术界的广泛关注。其中, 文献[5-11]考虑执行器或传感器失效故障情形, 分别对具有时延或(和)丢包的线性/非线性NCS的鲁棒完整性、鲁棒H_∞完整性及鲁棒保性能容错控制进行了研究。文献[12]给出了不确定NCS在α -稳定、H_∞扰动衰减指标和广义H₂三类指标共同约束下的满意容错设计准则。文献[13]探讨了参数不确定NCS同时受到执行器饱和、控制器参数摄动及非线性扰动时的鲁棒容错多约束控制问题。然而, 上述成果均是基于周期时间触发通讯机制(Periodic time-triggered communication scheme, PTTCS), 即在等间隔的离散时刻点上周期性地传输并更新控制信号, 尽管这样可以使系统的分析和设计更加便利, 但在NCS中网络通信带宽资源非常有限的情况下, 如若系统状态在当前时刻与上一时刻变化微小时, 按此机制通讯, 则会使大量不必要的冗余信息被传输, 这不仅浪费了有限的网络资源, 更会加剧网络时延、丢包等问题。因此, 如何在保证NCS期望性能得到满足的前提下, 更有效地利用网络资源变成了NCS研究中亟待解决的问题。

近期, 一种新的离散事件触发通讯机制^[14](Discrete event-triggered communication scheme, DETCS)被提出, 在此机制下, 数据传输是根据控制任务按需进行的, 相对PTTCS下所有采样数据传输都需通过有限带宽的通信网络实现的NCS来说, 信息量按需传输可以更为合理且有效地利用网络资源。文献[15, 16]在DETCS下, 分别对线性和T-S模糊NCS, 通过构造不同离散事件触发条件, 初步研究了系统H_∞滤波和稳定性问题。但未考虑NCS中元部件故障, 即系统无容错能力。此外, 考虑实际工程中, 由于自身物理特性限制和人为界定, 执行器饱和问题也常常存在^[17], 而且当系统发生故障后, 过大的控制量会使执行器更易进入饱和区, 因此, 基于DETCS, 考虑执行器饱和约束和元部件故障, 兼顾系统控制性能(Quality of performance, QoP)和网络服务质量(Quality of service, QoS)的NCS容错控制研究更具实际意义和研究价值。

鉴于上述分析, 本文拟从网络有限带宽占用率和系统控制性能着眼, 在离散事件触发通讯机制下, 对具有执行器饱和约束的不确定非线性网络化控制系统(Nonlinear networked control system, NNCS)进行鲁棒容错和网络通讯的协同设计研究。首先, 将一类普通非线性系统转化为T-S模糊模型表示的参数不确定NCS, 同时考虑网络时变时延、执行器故障及饱和约束, 并结合DETCS构建一种新的离散事件触发闭环故障NNCS模型。然后, 通过构造适当的时滞依赖Lyaponov-Krasovkii泛函, 采用时延分段技术、新的互反凸组合引理, 本着对Lyaponov-Krasovkii泛函导数项尽可能少地放大原则, 推导出使闭环故障系统稳定的时滞且事件触发依赖的不变集准则, 并结合LMI(Linear matrix inequality)技术, 给出鲁棒容错控制器和离散事件触发条件权矩阵协同设计的方法。最后以一个仿真算例验证文中所述方法对执行器饱和下的故障NNCS容错及通讯资源节约等方面的有效性。

1 问题描述

1.1 离散事件触发通讯机制

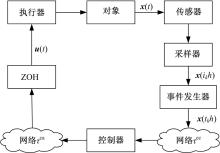
离散事件触发通讯机制是一种仅在采样时刻依据某种事件发生与否决定系统采样数据是否需要传输的通讯机制。基于此机制的NCS结构如图1所示。

	Figure Option View Download New Window
	图1 离散事件触发NCS结构图Fig.1 Structure of discrete event-triggered NCS

与传统的PTTCS下NCS结构图不同的是, 图1中在采样器后增加了事件发生器。其功能是根据事先设定的事件触发条件, 对采样数据进行筛选, 满足触发条件的采样信号则被传输给控制器; 反之则不被传输。

为了方便分析, 首先作如下假设:

假设1 传感器为时钟驱动, 具有恒定采样周期为h, 采样时刻记为i_kh, i_k=0, 1, 2, …, 采样数据为x(i_kh), 数据均采用单包传输, 系统所有状态均可测量。

假设2 控制器和执行器为事件驱动, 数据传输时刻记为t_kh, t_k=0, 1, 2, …, 传输数据为x(t_kh), 显然数据传输时刻的集合{t_kh, t_k=0, 1, 2, …}是采样时刻集合{i_kh, i_k=0, 1, 2, …}的子集。

假设3 若控制器采用静态状态反馈, 从事件发生器到控制器、控制器到执行器的传输时延, 以及控制器的计算时延可归并为 $\begin{matrix} τ_{t_{k}} \end{matrix}$ = $\begin{matrix} τ_{t_{k}}^{ec} \end{matrix}$ + $\begin{matrix} τ_{t_{k}}^{ca} \end{matrix}$ + $\begin{matrix} τ_{t_{k}}^{c} \end{matrix}$ 。

假设4 零阶保持器(ZOH)用来保持控制器传输来的最新数据包, 保持区域Ω =[t_kh+ $\begin{matrix} τ_{t_{k}} \end{matrix}$ , t_k+₁h+ $\begin{matrix} τ_{t_{k + 1}} \end{matrix}$ ], 其中:t_k+₁h为下一个数据包的传递时刻; t_kh+ $\begin{matrix} τ_{t_{k}} \end{matrix}$ 、t_k+₁h+ $\begin{matrix} τ_{t_{k + 1}} \end{matrix}$ 分别表示控制信号在t_k、t_k+₁到达ZOH的时刻, $\begin{matrix} τ_{t_{k}} \end{matrix}$ 、 $\begin{matrix} τ_{t_{k + 1}} \end{matrix}$ 分别表示t_kh, t_k+₁h时刻的网络传输时延。

基于上述假设, ZOH的保持区间(t∈ Ω )可划分为以下子集:Ω _l_,_k=[i_kh+ $\begin{matrix} τ_{i_{k}} \end{matrix}$ , i_kh+h+ $\begin{matrix} τ_{i_{k} + 1} \end{matrix}$ ], Ω =∪ Ω _l_,_k, 其中:i_kh=t_kh+lh, l=0, …, t_k+₁-t_k-1, 表示从当前数据包传递时刻t_kh到下一个最近数据包传递时刻t_k+₁h的间隔。

$\begin{matrix} \begin{matrix} 定义 τ (t) = t - i_{k} h, t \in Ω_{l, k} (1) \\ \overset{\cdot}{τ} (t) = 1 (2) \end{matrix} \end{matrix}$

且0< τ ₁≤ τ (t)≤ h+ $\begin{matrix} \bar{τ} \end{matrix}$ =τ ₂其中:τ ₁=min_l{ $\begin{matrix} τ_{i_{k}} \end{matrix}$ }、 $\begin{matrix} \bar{τ} \end{matrix}$ =max_l{ $\begin{matrix} τ_{i_{k} + 1} \end{matrix}$ }分别表示传输时刻网络时延的下、上界。

为了兼顾NCS期望性能的要求及网络通讯资源的节约使用, 引入如下离散事件触发条件:

$\begin{matrix} \begin{matrix} e^{T} (i_{k} h) Ve (i_{k} h) \geq δ_{1} x^{T} (i_{k} h) Vx (i_{k} h) (3) \\ ‖ x (i_{k} h) ‖ \geq δ_{2} > 0 (4) \end{matrix} \end{matrix}$

式中:V为正定的权矩阵; δ ₁> 0、δ ₂> 0为给定的标量参数, 与系统的期望性能指标有关; e(i_kh)表示当前采样时刻与最近数据传输时刻的状态差值, 简称状态误差, 其计算公式为:

$\begin{matrix} e (i_{k} h) = x (i_{k} h) - x (t_{k} h) (5) \end{matrix}$

若条件满足, 则t_k+₁h为下一个需要传输的数据包的时刻。

注1 从式(3)(4)可以看到, 引入DETCS后, 只有满足触发条件的部分采样数据x(i_kh)被传输至控制器, 因此可以预计, 只要触发参数选择适当, 这种通讯机制不仅会减少网络中的数据传输量和控制信号的计算量, 节约网络资源, 而且在满足控制需求的情形下, 使得数据的传输变为自适应变周期方式, 即DETCS可以改善PTTCS未考虑采样数据是否对更新控制信号有用, 就以定周期连续传输, 致使网络资源被大量冗余数据传输而占用的现状。

注2 与需要通过额外硬件设备对传感器输出量进行连续检测的连续事件触发通讯(Continuous event-triggered communication scheme, CETCS)方式相比^[18], 本文所采用的DETCS方式, 以一个常采样周期获取系统的状态量, 然后利用离散时刻采样点的测量状态计算触发条件, 无需关注采样时刻间状态信息的变化, 这使得DETCS的实现仅通过一般智能传感器或者软件即可完成, 省去了添加硬件的问题。

1.2 基于DETCS的执行器饱和闭环故障NNCS描述

1.2.1 被控对象

假设具有执行器饱和约束的非线性系统受控对象可描述为:

$\begin{matrix} \overset{\cdot}{x} (t) = F (x, u) = f (x (t)) + g (x (t)) sat (u (t)) (6) \end{matrix}$

式中:x(t)∈ Rⁿ、u(t)∈ R^m分别为系统的状态、控制输入向量; f(x(t))和g(x(t))分别在区域Rⁿ× Rⁿ内充分光滑, 且f(0)=0; sat(· ):Rⁿ→ R^m为标准饱和函数, 即sat(u)=[sat(u₁), sat(u₂), …, sat(u_m)]^T, sat(u_i)sign(u_i)min{1, |u_i|}。

由于T-S模糊模型能够利用模糊逻辑系统的非线性映射能力, 对定义在一个致密集上的复杂非线性系统做到任意精度的一致逼近。所以, 依据T-S模糊模型建模方法, 非线性系统(6)可表示为如下一些局部线性动态系统。

系统的模糊规则i:如果θ ₁(t)是F_i₁且…θ _n(t)是F_in, 则:

$\begin{matrix} \overset{\cdot}{x} (t) = A_{i} x (t) + B_{i} sat (u (t)) (7) \end{matrix}$

式中:θ (t)=[θ ₁(t), …, θ _n(t)]^T为模糊前件变量; F_ij为模糊集合, i=1, 2, …, r, j=1, 2, …, n, r为模糊推理规则数; A_i∈ R^{n× n}, B_i∈ R^{n× m}为适当维数的常数矩阵。

使用单点模糊化、乘积推理和平均加权反模糊化, 可得T-S全局动态模糊模型为:

$\begin{matrix} \overset{\cdot}{x} (t) = \overset{r}{\sum_{i = 1}} μ_{i} (θ (t)) [A_{i} x (t) + B_{i} sat (u (t))] (8) \end{matrix}$

式中:μ _i(θ (t))= $\begin{matrix} \frac{a_{i} (θ (t))}{\overset{n}{\sum_{i = 1}} a_{i} (θ (t))} \end{matrix}$ 为每个模糊规则的权重比, a_i(θ (t))= $\begin{matrix} \overset{n}{\prod_{j = 1}} \end{matrix}$ F_ij(θ _j(t)), F_ij(θ _j(t))为θ _j(t)关于F_ij的隶属函数。因为a_i(θ (t))≥ 0, 且: $\begin{matrix} \overset{n}{\sum_{i = 1}} \end{matrix}$ a_i(θ (t))> 0, 则μ _i(θ (t))≥ 0且 $\begin{matrix} \overset{r}{\sum_{i = 1}} \end{matrix}$ μ _i(θ (t))=1, ∀ t≥ 0。

为了简化描述, 记μ _i(θ (t))=μ _i。结合式(6)(8)可得:

$\begin{matrix} \overset{\cdot}{x} (t) = \overset{r}{\sum_{i = 1}} μ_{i} [A_{i} x (t) + B_{i} sat (u (t))] + Δf + Δg (9) \end{matrix}$

式中:Δ f+Δ g为非线性系统(6)和T-S全局模糊模型(8)之间的近似误差, 即建模误差, 且:

$\begin{matrix} \begin{matrix} Δf = f (x (t)) - \overset{r}{\sum_{i = 1}} μ_{i} A_{i} x (t) (10) \\ Δg = g (x (t)) sat (u (t)) - \overset{r}{\sum_{i = 1}} μ_{i} B_{i} sat (u (t)) (11) \end{matrix} \end{matrix}$

1.2.2 具有执行器饱和约束的闭环故障NNCS

对于系统(9), 采用如下状态反馈控制器。模糊控制规则i:如果θ ₁(t)是F_i₁且…θ _n(t)是F_in, 则

$\begin{matrix} u (t) = K_{i} x (t_{k} h), t \in Ω (12) \end{matrix}$

式中:K_i为控制器增益矩阵, i=1, 2, …, r。

结合式(1)(5), 则最近传输时刻的状态为:

$\begin{matrix} \begin{matrix} x (t_{k} h) = x (t - τ (t)) - e (i_{k} h), t \in Ω_{l, k} \\ (13) \end{matrix} \end{matrix}$

结合式(12)(13), 根据PDC算法, 考虑ZOH的动态属性, 可得模糊化状态反馈控制律为:

$\begin{matrix} \begin{matrix} u (t) = \overset{r}{\sum_{i = 1}} μ_{i} (θ (t)) K_{i} (x (t - τ (t)) - e (i_{k} h)) \\ t \in Ω_{l, k} (14) \end{matrix} \end{matrix}$

令l(K)={x₀∈ Rⁿ:|k_gx|≤ 1, g∈ [1, m]}, 矩阵K∈ R^{m× n}, k_g是K的第g行, 称l(K)为反馈控制的非饱和域, 或饱和反馈控制的线性域, 即对任意的x∈ ℓ(K), sat(Kx)=Kx。

考虑执行器可能发生失效故障的情形, 其故障模型描述为:

$\begin{matrix} u^{f} (t) = Mu (t) (15) \end{matrix}$

式中:M={diag{m₁, m₂, …, m_n}, m_p∈ [0, 1], p=1, 2, …, n}为执行器故障矩阵, m_p=1表示第p个执行器正常, m_p=0表示第p个执行器完全失效, m_p∈ (0, 1)表示第p个执行器部分失效, M∈ Φ , Φ 为所有可能执行器失效故障模式的集合。

结合式(9)(14)(15), 可得基于DETCS的闭环故障NNCS为:

$\begin{matrix} \begin{matrix} \overset{\cdot}{x} (t) = \overset{r}{\sum_{i = 1}} \overset{r}{\sum_{j = 1}} μ_{i} μ_{j} [A_{i} x (t) + B_{i} M \times \\ sat (K_{j} (x (t - τ (t)) - e (i_{k} h)))] + Δf + Δg (16) \end{matrix} \end{matrix}$

假设存在适当维数的实常数矩阵D_i, E_ai和E_bi, 满足:

$\begin{matrix} \begin{matrix} Δf = \overset{r}{\sum_{i = 1}} μ_{i} D_{i} F_{i} (t) E_{ai} x (t) (17) \\ Δg = \overset{r}{\sum_{i = 1}} \overset{r}{\sum_{j = 1}} μ_{i} μ_{j} D_{i} F_{i} (t) E_{bi} M \times \\ sat [K_{j} (x (t - τ (t)) - e (i_{k} h))] x (t) (18) \end{matrix} \end{matrix}$

式中:F_i(t)为未知时变实值连续矩阵函数, 其元素Lebesgue可测, 且满足 $\begin{matrix} {F^{T}}_{i} \end{matrix}$ (t)F_i(t)≤ I, i=1, 2, …, r, ∀ t< 0(I为单位矩阵).

则系统(16)可进一步描述为如下具有参数不确定性的执行器饱和非线性网络化闭环故障系统(Nonlinear networked closed-loop fault system, NNCFS)为:

$\begin{matrix} \begin{matrix} \overset{\cdot}{x} (t) = \overset{r}{\sum_{i = 1}} \overset{r}{\sum_{j = 1}} μ_{i} μ_{j} [{\bar{A}}_{i} x (t) + {\bar{B}}_{i} M \times \\ sat (K_{j} (x (t - τ (t)) - e (i_{k} h)))] (19) \\ 式中 : \\ {\bar{A}}_{i} = A_{i} + Δ A_{i}, {\bar{B}}_{i} = B_{i} + Δ B_{i} (20) \end{matrix} \end{matrix}$

Δ A_i、Δ B_i为范数有界的时变参数不确定性矩阵, 且:

$\begin{matrix} [Δ A_{i}, Δ B_{i}] = D_{i} F_{i} (t) [E_{ai}, E_{bi}] (21) \end{matrix}$

x(t)=ϕ (t), t∈ [-τ ₂, 0], ϕ (t)为给定的初始向量值连续函数。

注3 式(19)中不仅包含了网络传输时延、执行器故障及饱和约束, 还包含了离散事件触发条件的状态误差, 自然而然地将网络属性、元部件故障、饱和约束及通讯机制集成于一个数学模型, 为NNCS的容错控制器与DETCS触发参数的协同设计做好了铺垫。

1.3 相关引理

为得到本文结果, 以下给出用到的4个引理。

引理1^[19] 给定矩阵K、H∈ R^{m× n}, 对于x∈ Rⁿ, 如果x∈ l(H), 则有:

$\begin{matrix} sat (Kx) \in co {Υ_{q} Kx + Υ_{q}^{-} Hx : q \in [1, 2^{m}]} (22) \end{matrix}$

式中:co{· }为Υ _qKx+ $\begin{matrix} Υ_{q}^{-} \end{matrix}$ Hx, Υ _q∈ Υ , q∈ [1, 2^m]组成的凸包; Υ 为一个m× m对角矩阵的集合, 且其对角线上的元素是1或0, Υ 含有2^m个元素。

假设Υ 的每个元素被标记为Υ _q, q∈ [1, 2^m], 即Υ ={Υ ₁:q∈ [1, 2^m]}。定义 $\begin{matrix} Υ_{q}^{-} \end{matrix}$ =I-Υ _q, 则 $\begin{matrix} Υ_{q}^{-} \end{matrix}$ ∈ Υ 。

引理2^[20] 假设f₁, f₂, …, f_N∶ R^m→ R在开集D的子集中有正值, D∈ R^m。那么, 在集合D中f_i的互反凸组合满足:

$\begin{matrix} \begin{matrix} \min_{{α_{i} | α_{i} > 0, \sum_{i} α_{i} = 1}} \sum_{i} \frac{1}{α_{i}} f_{i} (t) = \\ \sum_{i} f_{i} (t) + \max_{g_{i, j} (i)} \sum_{i \neq j} g_{i, j} (t) (23) \end{matrix} \end{matrix}$

式中:{g_i_,_j∶ R^m→ R, g_j_,_i(t)} g_i_,_j(t),

$\begin{matrix} [\begin{matrix} f_{i} (t) & g_{i, j} (t) \\ g_{i, j} (t) & f_{j} (t) \end{matrix}] \geq 0\} \end{matrix}$ 。

引理3^[21] 任意矩阵N∈ R^{n× n}, N=N^T≥ 0、标量γ > 0及向量值函数 $\begin{matrix} \overset{\cdot}{x} \end{matrix}$ ∶ [-γ , 0]→ Rⁿ, 有以下积分不等式成立:

$\begin{matrix} \begin{matrix} - γ \int_{-}^{γ} {\overset{\cdot}{x}}^{T} (s) N \overset{\cdot}{x} (s) ds \leq \\ {[\begin{matrix} x (t) \\ x (t - γ) \end{matrix}]}^{T} [\begin{matrix} - N & N \\ N & - N \end{matrix}] [\begin{matrix} x (t) \\ x (t - γ) \end{matrix}] (24) \end{matrix} \end{matrix}$

引理4^[22] 对于具有适当维数的矩阵Y、M和E, 其中Y=Y^T, 则:

$\begin{matrix} Y + MF (t) E + E^{T} F^{T} (t) M^{T} < 0 (25) \end{matrix}$

对所有满足F^T(t)F(t)≤ I的矩阵F(t)成立, 当且仅当存在常数ε > 0, 使得如下不等式成立:

$\begin{matrix} Y + εM M^{T} + ε^{- 1} E^{T} E < 0 (26) \end{matrix}$

2 问题描述

2.1 DETCS下执行器饱和NNCS鲁棒容错控制设计目标

针对执行器饱和约束及失效故障, 基于DETCS的不确定NNCS鲁棒容错控制的设计目标为:寻求状态反馈增益矩阵K_j(j=1, 2, …, r)与离散事件触发条件中的触发权矩阵V, 使得对所有可能的执行器失效故障M∈ Φ , 系统(19)具有鲁棒完整性并尽可能节约网络通讯资源。

2.2 DETCS下执行器饱和NNCS不变集条件

采用椭球域求取不变集, 进而估计吸引域。令P∈ R^{n× n}是一个正定矩阵, 对一个正数ρ , 定义椭球体ε (P, ρ )={x∈ Rⁿ, x^TPx≤ ρ }, 记ε (P)表示ε (P, 1)。

定理1 在DETCS(3)、(4)下, 考虑系统(19), 给定常数τ ₂> τ ₁> 0, δ ₁> 0, δ ₂> 0, δ ₃> 0, 如果存在对称正定矩阵P、Q₁、Q₂、S₁、S₂、R_κ(κ =1, 2, 3), 正定矩阵V及适当维数的矩阵K_j、H_j(j=1, 2, …, r), 使得对任意可能的执行器失效故障模式M和可接受的参数不确定性, 满足下列矩阵不等式:

$\begin{matrix} \begin{matrix} [\begin{matrix} Ξ_{1} & {Π^{T}}_{1} & {Π^{T}}_{1} & {Π^{T}}_{1} \\ * & - (τ_{1}^{2} R_{1})^{- 1} & 0 & 0 \\ * & * & - (δ_{3}^{2} R_{2})^{- 1} & 0 \\ * & * & * & - (δ_{3}^{2} R_{3})^{- 1} \end{matrix}] < 0 \\ q \in [1, 2^{m}] (27) \\ [\begin{matrix} R_{2} & S_{1} \\ * & R_{2} \end{matrix}] \geq 0 (28) \\ [\begin{matrix} R_{3} & S_{2} \\ * & R_{3} \end{matrix}] \geq 0 (29) \end{matrix} \end{matrix}$

式中:* 是由矩阵对称性得到的矩阵块;

Ξ ₁= $\begin{matrix} [\begin{matrix} Ξ_{11}^{1} & Ξ_{12}^{1} & R_{1} & 0 & 0 & Ξ_{16}^{1} \\ * & Ξ_{22}^{1} & Ξ_{23}^{1} & Ξ_{24}^{1} & Ξ_{25}^{1} & 0 \\ * & * & Ξ_{33}^{1} & S_{1} & 0 & 0 \\ * & * & * & Ξ_{44}^{1} & S_{2} & 0 \\ * & * & * & * & - Q_{2} - R_{3} & 0 \\ * & * & * & * & * & - V \end{matrix}] \end{matrix}$ ;

$\begin{matrix} Ξ_{11}^{1} \end{matrix}$ =2 $\begin{matrix} {\bar{PA}}_{i} \end{matrix}$ +Q₁-R₁;

$\begin{matrix} Ξ_{44}^{1} \end{matrix}$ =-R₂-R₃;

$\begin{matrix} Ξ_{12}^{1} \end{matrix}$ = $\begin{matrix} {\bar{PB}}_{i} \end{matrix}$ M(Υ _qK_j+ $\begin{matrix} Υ_{q}^{-} \end{matrix}$ H_j);

$\begin{matrix} Ξ_{16}^{1} \end{matrix}$ =- $\begin{matrix} {\bar{PB}}_{i} \end{matrix}$ M(Υ _qK_j+ $\begin{matrix} Υ_{q}^{-} \end{matrix}$ H_j);

$\begin{matrix} Ξ_{22}^{1} \end{matrix}$ =-2R₂-2R₃+2S₁+2S₂+δ ₁V+ $\begin{matrix} δ_{2}^{2} \end{matrix}$ I;

$\begin{matrix} Ξ_{23}^{1} \end{matrix}$ =R₂-S₁;

$\begin{matrix} Ξ_{24}^{1} \end{matrix}$ =R₂+R₃-S₁-S₂;

$\begin{matrix} Ξ_{25}^{1} \end{matrix}$ =R₃-S₂;

$\begin{matrix} Ξ_{33}^{1} \end{matrix}$ =-Q₁+Q₂-R₁-R₂。

当Π ₁=[ $\begin{matrix} {\bar{A}}_{i} \end{matrix}$ $\begin{matrix} {\bar{B}}_{i} \end{matrix}$ M(Υ _qK_j+ $\begin{matrix} Υ_{q}^{-} \end{matrix}$ H_j) 0 0 0 - $\begin{matrix} {\bar{B}}_{i} \end{matrix}$ M(Υ _qK_j+ $\begin{matrix} Υ_{q}^{-} \end{matrix}$ H_j)]和ε (P)⊂l(H_j)时, 则存在鲁棒容错控制器(14)使得具有执行器饱和约束的NNCFS(19)渐近稳定, 且系统状态轨迹仍能保持在不变集ε (P)内。

证明构造Lyapunov-Krasovskii泛函:

$\begin{matrix} \begin{matrix} V (x (t)) = V_{1} (x (t)) + V_{2} (x (t)) (30) \\ V_{1} (x (t)) = x^{T} (t) Px (t) + \\ \int_{t}^{-} x^{T} (s) Q_{1} x (s) ds + \\ \int_{t}^{-} x^{T} (s) Q_{2} x (s) ds (31) \\ V_{2} (x (t)) = τ_{1} \int_{-}^{τ_{1}} \int_{t}^{+} {\overset{\cdot}{x}}^{T} (s) R_{1} \overset{\cdot}{x} (s) dsdθ + \\ (τ_{av} - τ_{1}) \int_{-}^{τ_{av}} \int_{t}^{+} {\overset{\cdot}{x}}^{T} (s) R_{2} \overset{\cdot}{x} (s) dsdθ + \\ (τ_{2} - τ_{av}) \int_{-}^{τ_{2}} \int_{t}^{+} {\overset{\cdot}{x}}^{T} (s) R_{3} \overset{\cdot}{x} (s) dsdθ (32) \end{matrix} \end{matrix}$

式中:P^T=P> 0, $\begin{matrix} {Q^{T}}_{1} \end{matrix}$ =Q₁> 0, $\begin{matrix} {Q^{T}}_{2} \end{matrix}$ =Q₂> 0, $\begin{matrix} {R^{T}}_{κ} \end{matrix}$ =R_κ> 0, (κ =1, 2, 3), τ _av=τ ₁+(τ ₂-τ ₁)/2。

沿着系统(19)的任意轨迹对V(x(t))求导, 得:

$\begin{matrix} \begin{matrix} {\overset{\cdot}{V}}_{1} (x (t)) = 2 x^{T} (t) P \overset{\cdot}{x} (t) + x^{T} (t) Q_{1} x (t) - \\ x^{T} (t - τ_{1}) Q_{1} x (t - τ_{1}) + \\ x^{T} (t - τ_{1}) Q_{2} x (t - τ_{1}) - \\ x^{T} (t - τ_{2}) Q_{2} x (t - τ_{2}) (33) \end{matrix} \end{matrix}$

根据引理1, 得:

$\begin{matrix} \begin{matrix} \overset{\cdot}{x} (t) \leq \max_{q \in [1, 2^{m}]} \overset{r}{\sum_{i = 1}} \overset{r}{\sum_{j = 1}} μ_{i} μ_{j} [{\bar{A}}_{i} x (t) + \\ {\bar{B}}_{i} M (Υ_{q} K_{j} (x (t - τ (t)) - e (i_{k} h)) + \\ Υ_{q}^{-} H_{j} (x (t - τ (t)) - e (i_{k} h)))] (34) \\ {\overset{\cdot}{V}}_{2} (x (t)) = {\overset{\cdot}{x}}^{T} (t) Θ \overset{\cdot}{x} (t) - \\ τ_{1} \int_{t}^{-} {\overset{\cdot}{x}}^{T} (s) R_{1} \overset{\cdot}{x} (s) ds - \\ (τ_{av} - τ_{1}) \int_{t}^{-} {\overset{\cdot}{x}}^{T} (s) R_{2} \overset{\cdot}{x} (s) ds - \\ (τ_{2} - τ_{av}) \int_{t}^{-} {\overset{\cdot}{x}}^{T} (s) R_{3} \overset{\cdot}{x} (s) ds (35) \\ Θ = τ_{1}^{2} R_{1} + (τ_{av} - τ_{1})^{2} R_{2} + (τ_{2} - τ_{av})^{2} R_{3} (36) \end{matrix} \end{matrix}$

结合式(34)(36), 得:

$\begin{matrix} {\overset{\cdot}{x}}^{T} (t) Θ \overset{\cdot}{x} (t) = ζ^{T} (t) {Π^{T}}_{1} Θ Π_{1} ζ (t) (37) \end{matrix}$

式中:ζ ^T(t)=[x^T(t) x^T(t-τ (t)) x^T(t-τ ₁) x^T(t-τ _av) x^T(t-τ ₂) e^T(i_kh)]。

根据引理3, 得:

$\begin{matrix} \begin{matrix} - τ_{1} \int_{t}^{-} {\overset{\cdot}{x}}^{T} (s) R_{1} \overset{\cdot}{x} (s) ds \leq \\ {[\begin{matrix} x (t) \\ x (t - τ_{1}) \end{matrix}]}^{T} [\begin{matrix} - R_{1} & R_{1} \\ R_{1} & - R_{1} \end{matrix}] [\begin{matrix} x (t) \\ x (t - τ_{1}) \end{matrix}] (38) \end{matrix} \end{matrix}$

根据互反凸组合引理2, 得:

$\begin{matrix} \begin{matrix} - (τ_{av} - τ_{1}) \int_{t}^{-} {\overset{\cdot}{x}}^{T} (s) R_{2} \overset{\cdot}{x} (s) ds \leq \\ - {[\begin{matrix} x (t - τ_{1}) - x (t - τ (t)) \\ x (t - τ (t)) - x (t - τ_{av}) \end{matrix}]}^{T} [\begin{matrix} R_{2} & S_{1} \\ * & R_{2} \end{matrix}] \times \\ [\begin{matrix} x (t - τ_{1}) - x (t - τ (t)) \\ x (t - τ (t)) - x (t - τ_{av}) \end{matrix}] (39) \end{matrix} \end{matrix}$

式中: $\begin{matrix} [\begin{matrix} R_{2} & S_{1} \\ * & R_{2} \end{matrix}] \end{matrix}$ ≥ 0。

同理, 得:

$\begin{matrix} \begin{matrix} - (τ_{2} - τ_{av}) \int_{t}^{-} {\overset{\cdot}{x}}^{T} (s) R_{3} \overset{\cdot}{x} (s) ds \leq \\ - {[\begin{matrix} x (t - τ_{av}) - x (t - τ (t)) \\ x (t - τ (t)) - x (t - τ_{2}) \end{matrix}]}^{T} [\begin{matrix} R_{3} & S_{2} \\ * & R_{3} \end{matrix}] \times \\ [\begin{matrix} x (t - τ_{av}) - x (t - τ (t)) \\ x (t - τ (t)) - x (t - τ_{2}) \end{matrix}] (40) \end{matrix} \end{matrix}$

式中: $\begin{matrix} [\begin{matrix} R_{3} & S_{2} \\ * & R_{3} \end{matrix}] \end{matrix}$ ≥ 0。

对于通讯机制(3)、(4), 当i_kh∈ Ω 时, 显然:

$\begin{matrix} \begin{matrix} e^{T} (i_{k} h) Ve (i_{k} h) < δ_{1} x^{T} (t_{k} h) Vx (t_{k} h) \\ (41) \\ ‖ x (i_{k} h) ‖ < δ_{2} (42) \end{matrix} \end{matrix}$

根据式(33)~式(42), 则有:

$\begin{matrix} \begin{matrix} \overset{\cdot}{V} (x (t)) = {\overset{\cdot}{V}}_{1} (x (t)) + {\overset{\cdot}{V}}_{2} (x (t)) + \\ e^{T} (i_{k} h) Ve (i_{k} h) - e^{T} (i_{k} h) Ve (i_{k} h) + \\ x^{T} (i_{k} h) x (i_{k} h) - x^{T} (i_{k} h) x (i_{k} h) \leq \\ \max_{q \in [1, 2^{m}]} \overset{r}{\sum_{i = 1}} \overset{r}{\sum_{j = 1}} μ_{i} μ_{j} ζ^{T} (t) (Ξ_{1} + {Π^{T}}_{1} Θ Π_{1}) ζ (t) - \\ x^{T} (i_{k} h) x (i_{k} h) (43) \end{matrix} \end{matrix}$

因为τ _av=τ ₁+(τ ₂-τ ₁)/2, 即τ ₂-τ _av=τ _av-τ ₁, 为简化描述, 令:

$\begin{matrix} \begin{matrix} δ_{3} = τ_{2} - τ_{av} = τ_{av} - τ_{1} (44) \\ 若 : \\ Ξ_{1} + {Π^{T}}_{1} Θ Π_{1} < 0 (45) \end{matrix} \end{matrix}$

应用Schur补引理, 式(45)转换为式(27)。即如果定理1成立, 则 $\begin{matrix} \overset{\cdot}{V} \end{matrix}$ (x(t))< 0, 从而可知控制律(14)可使基于DETCS的执行器饱和NNCFS(19)能够在吸引域ε (P)内稳定。

证毕。

注4 定理1中除了包含网络时延信息τ ₁、τ ₂外, 还包含了与状态误差e(i_kh)和以最近被传输状态x(t_kh)相关的离散事件触发条件参数δ ₁、δ ₂, 使得所得到的结论不仅是时滞依赖的, 而且也是状态误差及传输状态依赖的, 即时滞/事件触发共同依赖。当δ ₁、δ ₂趋于0时, t_k+₁h=t_kh+h, 此时所有的采样数据以常采样周期h通过通讯网络被传输, DETCS退化为PTTCS, 也即PTTCS下的容错设计仅为DETCS下容错设计的一种特例, 而DETCS下则兼顾了通讯资源的使用与系统性能。

注5 当i_kh∈ Ω 时, 式(41)成立, 假设V=I, 则式(41)可转换为:

$\begin{matrix} {||\frac{e (i_{k} h)}{x (t_{k} h)}||}_{2} < \sqrt{δ_{1}} (46) \end{matrix}$

根据L₂范数的工程意义, 若二次范数‖ · ‖ ₂为信号所具有的能量, 则式(46)左边表示状态误差信号与当前采样状态信号的能量比, 触发参数 $\begin{matrix} \sqrt{δ_{1}} \end{matrix}$ 则意味着状态变化的抑制率。当 $\begin{matrix} \sqrt{δ_{1}} \end{matrix}$ 减小时, 满足触发条件被传输的采样数据数将会增加, 网络资源的占用也将随之增大, 但控制性能会变好, 反之亦然。上式的变换, 可进一步看到触发条件(式(3))侧重于系统暂态过程的波动性, 而触发条件式(4)中δ ₂则更侧重于系统状态接近稳态的程度。

注6 定理1从减少保守性、降低计算复杂度角度出发来获取系统(19)稳定的不变集充分条件。其中, 在构造Lyapunov-Krasovskii泛函时, 运用了能够减少结论保守性的时延分段技术, 因需权衡保守性与计算效率, 本文选取分段数为2, 即, 式(30)中, 所构造的V₂(x(t))项包含了时延子区间[-τ _av, -τ ₁]和[-τ ₂, -τ _av]; 在推证时, 对Lyapunov-Krasovskii泛函导数项的放大处理, 本着既尽可能小的放大和不忽略任何有用项, 又不增加决策变量、加大计算量的原则, 未采用自由权矩阵方法, 而是采用了一种性能等价于积分不等式引理且决策变量数少于Jensen积分不等式的互反凸组合引理2^[20]。

2.3 DETCS下执行器饱和NNCS鲁棒容错控制器的设计方法

定理2 在DETCS(3)、(4)下, 考虑系统(19), 给定常数τ ₂> τ ₁> 0, δ ₁> 0, δ ₂> 0, δ ₃> 0, 如果存在对称正定矩阵X、 $\begin{matrix} {\tilde{Q}}_{1} \end{matrix}$ 、 $\begin{matrix} {\tilde{Q}}_{2} \end{matrix}$ 、 $\begin{matrix} {\tilde{S}}_{1} \end{matrix}$ 、 $\begin{matrix} {\tilde{S}}_{2} \end{matrix}$ 、 $\begin{matrix} {\tilde{R}}_{κ} \end{matrix}$ (κ =1, 2, 3), 正定矩阵 $\begin{matrix} \tilde{V} \end{matrix}$ 及适当维数的矩阵 $\begin{matrix} {\tilde{K}}_{j} \end{matrix}$ 、 $\begin{matrix} {\tilde{H}}_{j} \end{matrix}$ (j=1, 2, …, r), 使得对任意可能的执行器失效故障模式M和可接受的参数不确定性满足下列矩阵不等式:

$\begin{matrix} \begin{matrix} [\begin{matrix} Σ_{1} & {\tilde{Π}}^{T}_{2} & {\tilde{Π}}^{T}_{2} & {\tilde{Π}}^{T}_{2} & {\tilde{Π}}^{T}_{5} & {\tilde{Π}}^{T}_{6} & {\tilde{Π}}^{T}_{7} \\ * & Σ_{2} & 0 & 0 & D_{i} & 0 & 0 \\ * & * & Σ_{3} & 0 & D_{i} & 0 & 0 \\ * & * & * & Σ_{4} & D_{i} & 0 & 0 \\ * & * & * & * & - ε_{1}^{- 1} I & 0 & 0 \\ * & * & * & * & * & - ε_{1} I & 0 \\ * & * & * & * & * & * & - (δ_{2}^{2} {I)}^{- 1} \end{matrix}] < 0 \\ q \in [1, 2^{m}] (47) \\ [\begin{matrix} {\tilde{R}}_{2} & {\tilde{S}}_{1} \\ * & {\tilde{R}}_{2} \end{matrix}] \geq 0 (48) \\ [\begin{matrix} {\tilde{R}}_{3} & {\tilde{S}}_{2} \\ * & {\tilde{R}}_{3} \end{matrix}] \geq 0 (49) \\ [\begin{matrix} 1 & {\tilde{h}}_{g} \\ * & X \end{matrix}] \geq 0, g \in [1, m] (50) \end{matrix} \end{matrix}$

式中:* 是由矩阵对称性得到的矩阵块:

Σ ₁= $\begin{matrix} [\begin{matrix} Σ_{11}^{1} & Σ_{12}^{1} & {\tilde{R}}_{1} & 0 & 0 & Σ_{16}^{1} \\ * & Σ_{22}^{1} & Σ_{23}^{1} & Σ_{24}^{1} & Σ_{25}^{1} & 0 \\ * & * & Σ_{33}^{1} & {\tilde{S}}_{1} & 0 & 0 \\ * & * & * & Σ_{44}^{1} & {\tilde{S}}_{2} & 0 \\ * & * & * & * & - {\tilde{Q}}_{2} - {\tilde{R}}_{3} & 0 \\ * & * & * & * & * & - \tilde{V} \end{matrix}] \end{matrix}$ ;

$\begin{matrix} Σ_{11}^{1} \end{matrix}$ =A_iX+X $\begin{matrix} {A^{T}}_{1} \end{matrix}$ + $\begin{matrix} {\tilde{Q}}_{1} \end{matrix}$ - $\begin{matrix} {\tilde{R}}_{1} \end{matrix}$ ;

$\begin{matrix} Σ_{12}^{1} \end{matrix}$ =B_iM(Υ _q $\begin{matrix} {\tilde{K}}_{j} \end{matrix}$ + $\begin{matrix} Υ_{q}^{-} \end{matrix} \begin{matrix} {\tilde{H}}_{j} \end{matrix}$ );

$\begin{matrix} Σ_{16}^{1} \end{matrix}$ =-B_iM(Υ _q $\begin{matrix} {\tilde{K}}_{j} \end{matrix}$ + $\begin{matrix} Υ_{q}^{-} \end{matrix} \begin{matrix} {\tilde{H}}_{j} \end{matrix}$ );

$\begin{matrix} Σ_{22}^{1} \end{matrix}$ =-2 $\begin{matrix} {\tilde{R}}_{2} \end{matrix}$ -2 $\begin{matrix} {\tilde{R}}_{3} \end{matrix}$ +2 $\begin{matrix} {\tilde{S}}_{1} \end{matrix}$ +2 $\begin{matrix} {\tilde{S}}_{2} \end{matrix}$ +δ ₁ $\begin{matrix} \tilde{V} \end{matrix}$ ;

$\begin{matrix} Σ_{23}^{1} \end{matrix}$ = $\begin{matrix} {\tilde{R}}_{2} \end{matrix}$ - $\begin{matrix} {\tilde{S}}_{1} \end{matrix}$ ; $\begin{matrix} Σ_{24}^{1} \end{matrix}$ = $\begin{matrix} {\tilde{R}}_{2} \end{matrix}$ + $\begin{matrix} {\tilde{R}}_{3} \end{matrix}$ - $\begin{matrix} {\tilde{S}}_{1} \end{matrix}$ - $\begin{matrix} {\tilde{S}}_{2} \end{matrix}$ ;

$\begin{matrix} Σ_{25}^{1} \end{matrix}$ = $\begin{matrix} {\tilde{R}}_{3} \end{matrix}$ - $\begin{matrix} {\tilde{S}}_{2} \end{matrix}$ ; $\begin{matrix} Σ_{33}^{1} \end{matrix}$ =- $\begin{matrix} {\tilde{Q}}_{1} \end{matrix}$ + $\begin{matrix} {\tilde{Q}}_{2} \end{matrix}$ - $\begin{matrix} {\tilde{R}}_{1} \end{matrix}$ - $\begin{matrix} {\tilde{R}}_{2} \end{matrix}$ ;

$\begin{matrix} Σ_{44}^{1} \end{matrix}$ =- $\begin{matrix} {\tilde{R}}_{2} \end{matrix}$ - $\begin{matrix} {\tilde{R}}_{3} \end{matrix}$ ; Σ ₂=- $\begin{matrix} \frac{1}{τ_{1}^{2}} \end{matrix}$ (2X- $\begin{matrix} {\tilde{R}}_{1} \end{matrix}$ );

Σ ₃=- $\begin{matrix} \frac{1}{δ_{3}^{2}} \end{matrix}$ (2X- $\begin{matrix} {\tilde{R}}_{2} \end{matrix}$ ); Σ ₄=- $\begin{matrix} \frac{1}{δ_{3}^{2}} \end{matrix}$ (2X- $\begin{matrix} {\tilde{R}}_{3} \end{matrix}$ );

$\begin{matrix} {\tilde{Π}}_{2} \end{matrix}$ =[A_iX B_iM(Υ _q $\begin{matrix} {\tilde{K}}_{j} \end{matrix}$ + $\begin{matrix} Υ_{q}^{-} \end{matrix} \begin{matrix} {\tilde{H}}_{j} \end{matrix}$ ) 0 0 0

-B_iM(Υ _q $\begin{matrix} {\tilde{K}}_{j} \end{matrix}$ + $\begin{matrix} Υ_{q}^{-} \end{matrix} \begin{matrix} {\tilde{H}}_{j} \end{matrix}$ )];

$\begin{matrix} {\tilde{Π}}_{5} \end{matrix}$ =[ $\begin{matrix} {D^{T}}_{i} \end{matrix}$ 0 0 0 0 0];

$\begin{matrix} {\tilde{Π}}_{6} \end{matrix}$ =[E_aiX E_biM(Υ _q $\begin{matrix} {\tilde{K}}_{j} \end{matrix}$ + $\begin{matrix} Υ_{q}^{-} \end{matrix} \begin{matrix} {\tilde{H}}_{j} \end{matrix}$ ) 0 0 0

-E_biM(Υ _qK_j+ $\begin{matrix} Υ_{q}^{-} \end{matrix}$ H_j)];

$\begin{matrix} {\tilde{Π}}_{7} \end{matrix}$ =[0 X 0 0 0 0]。

执行器饱和参数不确定NNCFS(19)渐近稳定, 系统状态轨迹仍能保持在不变集ε (P)内, 且式(14)是一使得系统(19)具有鲁棒完整性的控制律, 控制器参数及离散事件触发权矩阵可分别由式K_j= $\begin{matrix} {\tilde{K}}_{j} \end{matrix}$ X^-¹; V=X^-¹ $\begin{matrix} \tilde{V} \end{matrix}$ X^-¹求得。

证明将式(20)(21)代入式(27), 式(27)等价为:

$\begin{matrix} \begin{matrix} [\begin{matrix} Ξ_{2} & {Π^{T}}_{2} & {Π^{T}}_{2} & {Π^{T}}_{2} \\ * & - (τ_{1}^{2} R_{1})^{- 1} & 0 & 0 \\ * & * & - (δ_{3}^{2} R_{2})^{- 1} & 0 \\ * & * & * & - (δ_{3}^{2} R_{3})^{- 1} \end{matrix}] + \\ {Π^{T}}_{3} F_{i} (t) Π_{4} + {Π^{T}}_{4} F_{i} (t) Π_{3} < 0 \\ (51) \end{matrix} \end{matrix}$

式中:

Ξ ₂= $\begin{matrix} [\begin{matrix} Ξ_{11}^{2} & Ξ_{12}^{2} & R_{1} & 0 & 0 & Ξ_{16}^{2} \\ * & Ξ_{22}^{1} & Ξ_{23}^{1} & Ξ_{24}^{1} & Ξ_{25}^{1} & 0 \\ * & * & Ξ_{33}^{1} & S_{1} & 0 & 0 \\ * & * & * & Ξ_{44}^{1} & S_{2} & 0 \\ * & * & * & * & - Q_{2} - R_{3} & 0 \\ * & * & * & * & * & - V \end{matrix}] \end{matrix}$ ;

$\begin{matrix} Ξ_{11}^{2} \end{matrix}$ =2PA_i+Q₁-R₁;

$\begin{matrix} Ξ_{12}^{2} \end{matrix}$ =PB_iM(Υ _qK_j+ $\begin{matrix} Υ_{q}^{-} \end{matrix}$ H_j);

$\begin{matrix} Ξ_{16}^{2} \end{matrix}$ =-PB_iM(Υ _qK_j+ $\begin{matrix} Υ_{q}^{-} \end{matrix}$ H_j);

Π ₂=[A_i B_iM(Υ _qK_j+ $\begin{matrix} Υ_{q}^{-} \end{matrix}$ H_j) 0 0 0

-B_iM(Υ _qK_j+ $\begin{matrix} Υ_{q}^{-} \end{matrix}$ H_j)];

Π ₃=[ $\begin{matrix} {D^{T}}_{i} \end{matrix}$ P^T 0 0 0 0 0 $\begin{matrix} {D^{T}}_{i} \end{matrix}$ $\begin{matrix} {D^{T}}_{i} \end{matrix}$ $\begin{matrix} {D^{T}}_{i} \end{matrix}$ ];

Π ₄=[E_ai E_biM(Υ _qK_j+ $\begin{matrix} Υ_{q}^{-} \end{matrix}$ H_j) 0 0 0

-E_biM(Υ _qK_j+ $\begin{matrix} Υ_{q}^{-} \end{matrix}$ H_j) 0 0 0]

应用引理4, 式(51)等价为:

$\begin{matrix} [\begin{matrix} Ξ_{2} & {Π^{T}}_{2} & {Π^{T}}_{2} & {Π^{T}}_{2} & {Π^{T}}_{5} & {Π^{T}}_{6} \\ * & Ξ_{3} & 0 & 0 & D_{i} & 0 \\ * & * & Ξ_{3} & 0 & D_{i} & 0 \\ * & * & * & Ξ_{3} & D_{i} & 0 \\ * & * & * & * & - ε_{1}^{- 1} I & 0 \\ * & * & * & * & * & - ε_{1} I \end{matrix}] < 0 (52) \end{matrix}$

式中:Ξ ₃=-( $\begin{matrix} τ_{1}^{2} \end{matrix}$ R₁)^-¹;

Ξ ₄=-( $\begin{matrix} δ_{3}^{2} \end{matrix}$ R₂)^-¹;

Ξ ₅=-( $\begin{matrix} δ_{3}^{2} \end{matrix}$ R₃)^-¹;

Π ₅=[ $\begin{matrix} {D^{T}}_{i} \end{matrix}$ P^T 0 0 0 0 0];

Π ₆=[E_ai E_biM(Υ _qK_j+ $\begin{matrix} Υ_{q}^{-} \end{matrix}$ H_j) 0 0 0

-E_biM(Υ _qK_j+ $\begin{matrix} Υ_{q}^{-} \end{matrix}$ H_j)]。

当 $\begin{matrix} R_{κ}^{- 1} \end{matrix}$ > 0, κ =1, 2, 3, 可得:

$\begin{matrix} \begin{matrix} (R_{κ}^{- 1} - P^{- 1}) R_{κ} (R_{κ}^{- 1} - P^{- 1}) \geq 0 \\ 则 : - R_{κ}^{- 1} \leq P^{- 1} R_{κ} P^{- 1} - 2 P^{- 1} (53) \end{matrix} \end{matrix}$

将式(53)代入式(52), 应用Schur补引理, 并对变换后的结果进行合同变换, 即两端同时乘以对角矩阵diag{P^-¹, P^-¹, P^-¹, P^-¹, P^-¹, P^-¹, I, I, I, I, I}, 并令P^-¹=X; XS₁X= $\begin{matrix} {\tilde{S}}_{1} \end{matrix}$ ; XS₂X= $\begin{matrix} {\tilde{S}}_{2} \end{matrix}$ ; XQ₁X= $\begin{matrix} {\tilde{Q}}_{1} \end{matrix}$ ; XQ₂X= $\begin{matrix} {\tilde{Q}}_{2} \end{matrix}$ ; XR_κX= $\begin{matrix} {\tilde{R}}_{κ} \end{matrix}$ , κ =1, 2, 3; XVX= $\begin{matrix} \tilde{V} \end{matrix}$ ; K_jX= $\begin{matrix} {\tilde{K}}_{j} \end{matrix}$ ; H_jX= $\begin{matrix} {\tilde{H}}_{j} \end{matrix}$ , j=1, 2, …, r, 得式(47)。

同样对式(28)(29)两端同时乘以对角矩阵diag{P^-¹, P^-¹}则可得式(48)(49)。

对执行器饱和反馈控制的线性域条件做如下变换:

$\begin{matrix} \begin{matrix} ε (P) \subset l (H_{j}) \Leftrightarrow | h_{g} x | \leq 1, \forall x \in ε (P), \\ g \in [1, m], h_{g} 为 {\tilde{H}}_{j} 的第 g 行 \\ \Leftrightarrow h_{g} P^{- 1} {h^{T}}_{g} \leq 1 \\ \Leftrightarrow [\begin{matrix} 1 & h_{g} P^{- 1} \\ * & P^{- 1} \end{matrix}] \geq 0, g \in [1, m] (54) \end{matrix} \end{matrix}$

因为P^-¹=X, H_jX= $\begin{matrix} {\tilde{H}}_{j} \end{matrix}$ , 所以式(54)等价于式(50), 即满足式(47)~(50), 控制律(14)使得系统(19)渐近稳定, 控制器参数可由K_j= $\begin{matrix} {\tilde{K}}_{j} \end{matrix}$ X^-¹求得, 离散事件触发权矩阵可由V=X^-¹ $\begin{matrix} \tilde{V} \end{matrix}$ X^-¹求得。

证毕。

注7 本文所研究的执行器饱和NNCS鲁棒容错控制的设计方法, 并未孤立求取控制器增益, 而是通过离散事件触发条件参数δ ₁、δ ₂的合理设定, 兼顾QoP和QoS, 折中平衡系统性能与网络通讯量, 进行了鲁棒容错控制器K_j与离散事件触发条件权矩阵V的协同设计。

3 仿真

考虑闭环系统(19), 采用文献[11]的非线性系统模型数据。

系统模糊规则如下:

Rule 1:if x₁(t) is μ ₁, then

$\begin{matrix} \overset{\cdot}{x} \end{matrix}$ (t)= $\begin{matrix} {\bar{A}}_{1} \end{matrix}$ x(t)+ $\begin{matrix} {\bar{B}}_{1} \end{matrix}$ Msat(u(t))

Rule 2:if x₂(t) is μ ₂, then

$\begin{matrix} \overset{\cdot}{x} \end{matrix}$ (t)= $\begin{matrix} {\bar{A}}_{2} \end{matrix}$ x(t)+ $\begin{matrix} {\bar{B}}_{2} \end{matrix}$ Msat(u(t))

选用模糊隶属度函数为:μ ₁(x₁(t))=sin²(x₁(t))和μ ₂(x₁(t))=cos²(x₁(t))。

式中:A₁= $\begin{matrix} [\begin{matrix} - 3 & 1 \\ 1 & - 1 \end{matrix}] \end{matrix}$ ; A₂= $\begin{matrix} [\begin{matrix} - 2 & 1 \\ 1 & 0 \end{matrix}] \end{matrix}$ ; B₁= $\begin{matrix} [\begin{matrix} 1 & 0 \\ 0 & 0.7 \end{matrix}] \end{matrix}$ ; B₂= $\begin{matrix} [\begin{matrix} 1 & 0 \\ 0 & 0.5 \end{matrix}] \end{matrix}$ ; D₁=D₂= $\begin{matrix} [\begin{matrix} 0.1 & 0 \\ 0 & 0.1 \end{matrix}] \end{matrix}$ ;

Ea_i=Eb_i= $\begin{matrix} [\begin{matrix} 0 & 0.1 \\ 0.1 & 0 \end{matrix}] \end{matrix}$ , i=1, 2;

F₁(t)=F₂(t)= $\begin{matrix} [\begin{matrix} sint & 0 \\ 0 & cost \end{matrix}] \end{matrix}$ 。

通过计算得出:A₁的特征值为-3.4142, -0.5858; A₂的特征值为-2.4142, 0.4142, 即系统在未引入控制器时是不稳定的。

3.1 有效性验证

针对执行器正常和各种失效故障情形, 取:M₀=diag{1, 1}表示执行器正常, M₁=diag{0, 1}, M₂=diag{1, 0}分别表示执行器1、执行器2发生完全失效故障, M₃=diag{0.89, 0.12}表示执行器1、2发生部分失效故障。

若采样周期h=0.1 s, 实际网络传输时延上、下界分别为 $\begin{matrix} \bar{τ} \end{matrix}$ =0.15 s, τ ₁=0.01 s, 则τ ₂=0.25 s, τ _av=0.13 s。取触发参数δ ₁=0.7, δ ₂=0.02, 由定理2, 通过求解LMIs(47)~(50), 可得鲁棒容错控制器增益矩阵为:

K₁= $\begin{matrix} [\begin{matrix} - 0.2426 & - 0.5855 \\ - 0.0167 & - 0.0402 \end{matrix}] \end{matrix}$ ;

K₂= $\begin{matrix} [\begin{matrix} - 0.2430 & - 0.5866 \\ - 0.0164 & - 0.0395 \end{matrix}] \end{matrix}$ ;

相应的离散事件触发权矩阵为:

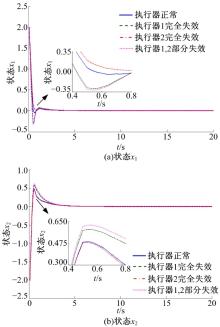
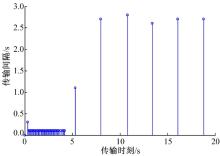
V= $\begin{matrix} [\begin{matrix} 22.7081 & 54.7589 \\ 54.7589 & 132.1500 \end{matrix}] \end{matrix}$

取系统初始状态为x(0)=[2 -2]^T, 此时执行器在正常M₀和发生M₁、M₂、M₃故障情形下, 其状态分量x₁、x₂的响应曲线图分别如图2(a)(b)所示, 离散事件触发NNCS数据实际传输时刻与传输间隔关系如图3所示。

	Figure Option View Download New Window
	图2 闭环系统状态响应曲线Fig.2 Response curve of state of closed-loop system

	Figure Option View Download New Window
	图3 事件触发NCS数据传输时刻与传输间隔关系Fig.3 Release instants and release interval of event-triggered NCS

(1)从图2(a)(b)可以看出:引入DETCS后, 对于不同执行器失效故障情形, 即使执行器具有饱和约束, 不确定NNCS仍是渐近稳定的。说明采用本文方法, 使得在DETCS下所设计的鲁棒容错控制器对NNCS执行器故障的容错是有效的。进而结合图2(a)(b), 从图3中可看出:当系统状态趋于平衡点附近后, 离散事件触发条件满足的机率减少, 传输数据在3.9 s后变得稀疏, 通讯频率较暂态过程明显减少, 通讯周期自然变大, 这表明在DETCS下, 信息完全按需传输, 且依据系统当前状态和状态变化量是否满足触发条件, 数据的传输方式从常周期变为了自适应变周期的传输方式。

(2)依据上述仿真, 在DETCS下, 离散事件触发参数δ ₁=0.7, δ ₂=0.02时, 20 s的仿真时间内, 系统实际数据传输量为n=47, 平均传输周期为:

$\begin{matrix} \begin{matrix} \bar{h} = 运行时间段 / 实际传输数据量 = \\ 20 / 47 = 0.426 s \end{matrix} \end{matrix}$

数据传输率为:

$\begin{matrix} \frac{实际传输数据量}{所有采样数据量} = \frac{47}{200} = 23.5 % \end{matrix}$

可以看到与PTTCS(传输周期为0.1 s, 20 s内传输量为200个)相比, 系统实际传输数据减少了153个, 平均传输周期增大了0.326 s, 数据传输率节省了76.5%。这表明与依靠物理时钟驱动进行数据传输的PTTCS相比较, 依据系统性能需求、实时状态及其变化量完成系统状态传输的DETCS的引入, 可有效地减少网络通讯负载, 节约网络资源。

3.2 DETCS下触发参数对通讯资源占用及系统性能的影响分析

上述仿真对结论有效性进行了验证, 下面分别选取不同的触发参数δ ₁、δ ₂, 分析说明采样周期h=0.1 s, 控制时段T=20 s时, 随着触发参数的变化, 系统性能及网络通讯资源的占用情况。

由表1和表2可以看出:在给定的20 s控制时段内, 随着触发参数δ ₁或δ ₂的不断增大, 需传输的数据n和数据传输率γ _e/t逐渐减少, 数据平均传输周期 $\begin{matrix} \bar{h} \end{matrix}$ 及相应的网络资源节省率(1-γ _e/t)逐渐变大, 即大的触发参数值δ ₁、δ ₂的选取, 可更多地节省网络通讯资源, 但一味地增大δ ₁、δ ₂, 过分追求网络资源的节约时, LMIs已无可行解, 即系统将以丧失容错能力为代价。因此, 离散事件触

表1 δ ₂=0.02不同触发参数δ ₁下的相关量比较 Table 1 Comparison results of relevant variable for different trigger parameter δ ₁ and given δ ₂=0.02

参数	δ ₁	n	$\begin{matrix} \bar{h} \end{matrix}$	γ _e/t/%
离散事件触发	0.5	147	0.136	73.5
	0.6	126	0.158	63
	0.65	64	0.313	32
	0.7	47	0.426	23.5
	0.8	32	0.625	16
	≥ 1.05	定理2中LMIs不可行

表1 δ ₂=0.02不同触发参数δ ₁下的相关量比较 Table 1 Comparison results of relevant variable for different trigger parameter δ ₁ and given δ ₂=0.02

表2 δ ₁=0.7不同触发参数δ ₂下的相关量比较 Table 2 Comparison results of relevant variable for different trigger parameter δ ₂ and given δ ₁=0.7

参数	δ ₂	n	$\begin{matrix} \bar{h} \end{matrix}$	γ _e/t/%
离散事件触发	0.002	48	0.417	24
	0.02	47	0.426	23.5
	0.04	38	0.526	19.5
	0.06	35	0.571	17.5
	≥ 0.07	定理2中LMIs不可行

表2 δ ₁=0.7不同触发参数δ ₂下的相关量比较 Table 2 Comparison results of relevant variable for different trigger parameter δ ₂ and given δ ₁=0.7

发条件中触发参数的合理选择, 可使系统期望性能与通讯资源占用折中平衡, 从而实现NCS鲁棒容错控制与网络资源有效利用的协同设计目标。

4 结束语

在DETCS下, 针对具有执行器饱和约束的NNCS, 考虑网络诱导时延及更一般的执行器失效故障, 建立了离散事件触发闭环故障NNCS模型, 然后基于所建模型推证出使系统稳定的时滞且事件触发依赖的不变集充分条件, 并以LIMs方式给出了兼顾网络资源节约利用和系统性能协同设计的鲁棒容错控制器求解方法。最后通过仿真算例验证了文中所述方法可以在DETCS下, 使得饱和NNCS具有容错性能的同时节约了网络资源。进而还通过不同触发参数的选择, 计算分析了该参数与通讯资源、系统性能之间的关系, 得出了离散事件触发参数δ ₁、δ ₂的增大, 可使更多的网络资源被节省, 但同时会使系统性能降低的结论。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Hespanha J P, Naghshtabrizi P, Xu Y G. A survey of recent results in networked control systems[J]. Proceedings of the IEEE, 2007, 95(1): 138-162. [本文引用:1]
[2]	杨丽, 关新平, 罗小元, 等. 具有包丢失和时延的网络控制系统的随机稳定性[J]. 吉林大学学报: 工学版, 2010, 40(1): 130-135. Yang Li, Guan Xin-ping, Luo Xiao-yuan, et al. Stochastic stability of networked control system with data packet loss and time delay[J]. Journal of Jilin University (Engineering and Technology Edition), 2010, 40(1): 130-135. [本文引用:1]
[3]	Donkers M C F, Heemels W P M H, Bernardini D, et al. Stability analysis of stochastic networked control systems[J]. Automatica, 2012, 48(5): 917-925. [本文引用:1]
[4]	Peng Chen, Fei Min-rui. An improved result on the stability of uncertain T-S fuzzy systems with interval time-varying delay[J]. Fuzzy Sets and Systems, 2013, 212: 97-109. [本文引用:1]
[5]	Tian En-gang, Yue Dong, Peng Chen. Reliable control for networked control systems with probabilistic actuator fault and rand om delays[J]. Journal of the Franklin Institute, 2010, 347(10): 1907-1926. [本文引用:1]
[6]	Huo Zhi-hong, Zheng Yuan, Xu Chang. A robust fault-tolerant control strategy for networked control systems[J]. Journal of Network and Computer Applications, 2011, 34(2): 708-714. [本文引用:1]
[7]	Zhao Ming-yue, Liu He-ping, Li Zhi-jun, et al. Fault tolerant control for networked control systems with packet loss and time delay[J]. International Journal of Automation and Computing, 2011, 8(2): 244-253. [本文引用:1]
[8]	李炜, 王艳飞. 少保守性网络化控制系统鲁棒保性能容错控制[J]. 兵工学报, 2012, 33(2): 170-178. Li Wei, Wang Yan-fei. The less-conservative robust guaranteed cost fault-tolerant control of networked control systems[J]. Acta Armamentarii, 2012, 33(2): 170-178. [本文引用:1]
[9]	Yang Fei-sheng, Zhang Hua-guang, Hui Guo-tao, et al. Mode-independent fuzzy fault-tolerant variable sampling stabilization of nonlinear networked systems with both time-delay and rand om delays[J]. Fuzzy Sets and Systems, 2012, 3(4): 1-19. [本文引用:1]
[10]	Yin Zuo-you, Kang Yun-xia, Chang Xiao-heng, et al. Robust H-infinity fault tolerant control for a class of nonlinear networked control systems based on T-S fuzzy model[C]∥Proceedings of the 2012 24th Chinese Control and Decision Conference, Taiyuan, China, 2012: 2292-2296. [本文引用:1]
[11]	王君, 李炜, 李战明. 基于T-S模型的不确定NNCS鲁棒容错保性能设计[J]. 系统工程与电子技术, 2011, 33(10): 2288-2294. Wang Jun, Li Wei, Li Zhan-ming. Robust guaranteed fault-tolerant design for uncertain NNCS based on T-S model[J]. System Engineering and Electronics, 2011, 33(10): 2288-2294. [本文引用:1]
[12]	李炜, 申富媛. 具有α-稳定的NCS满意容错设计[J]. 控制工程, 2013, 20(1): 149-154. Li Wei, Shen Fu-yuan. Satisfactory fault-tolerant design of NCS with α-stability[J]. Control Engineering of China, 2013, 20(1): 149-154. [本文引用:1]
[13]	曹慧超, 李炜. 执行器饱和不确定NCS非脆弱鲁棒容错控制[J]. 控制与决策, 2013, 28(12): 1874-1883. Cao Hui-chao, Li Wei. Non-fragile robust fault-tolerant control for uncertain NCS with actuator saturation[J]. Control and Decision, 2013, 28(12): 1874-1883. [本文引用:1]
[14]	Yue Dong, Tian En-gang, Han Qing-long. A delay system method to design of event-triggered control of networked control systems[C]∥2011 50th IEEE Conference on Decision and Control and European Control Conference, Orland o, USA, 2011: 1668-1673. [本文引用:1]
[15]	Hu Song-ling, Yue Dong. Event-based filtering for networked system with communication delay[J]. Signal Processing, 2012, 92(9): 2029-2039. [本文引用:1]
[16]	Peng Chen, Han Qing-long, Yue Dong. To transmit or not to transmit: a discrete event-triggered communication scheme for networked Takagi-Sugeno fuzzy systems[J]. IEEE Transactions on Fuzzy Systems, 2013, 21(1): 164-170. [本文引用:1]
[17]	魏爱荣, 王玉振, 赵克友. 含状态时滞及执行器饱和不确定系统反馈镇定及L2增益分析[J]. 控制理论与应用, 2007, 24(3): 475-479. Wei Ai-rong, Wang Yu-zhen, Zhao Ke-you. Feedback stabilization and L2-gain analysis of uncertain systems withstate delay and actuator saturation[J]. Control Theory&Applications, 2007, 24(3): 475-479. [本文引用:1]
[18]	Wang X F, Lemmon M. Event-triggering in distributed networked systems with data dropouts and delays[C]∥Hybrid Systems: Computation and Control- 12th International Conference, San Francisco, USA, 2009: 366-380. [本文引用:1]
[19]	Hu T S, Lin Z L, Chen B M. Analysis and design for discrete-time linear systems subject to actuator saturation[J]. Systems and Control Letters, 2002, 45(2): 97-112. [本文引用:1]
[20]	PooGyeon P, Jeong W K, Changki J. Reciprocally convex approach to stability of systems with time-varying delays[J]. Automatica, 2011, 47(1): 235-238. [本文引用:2]
[21]	Han Qing-long. Absolute stability of time-delay systems with sector-bounded nonlinearity[J]. Automatica, 2005, 41(12): 2171-2176. [本文引用:1]
[22]	Xie Li-hua. Output feedback control of systems with parameter uncertainty[J]. International Journal of Control, 1996, 63(4): 741-750. [本文引用:1]

2007

0.0

... 0 引言目前,针对数据通过网络传输时产生的时延、丢包、乱序等影响系统性能的问题,已在网络化控制系统(Networked control system,NCS)稳定性分析和控制器设计等方面开展了大量的研究工作^[1,2,3,4] ...

2010

0.0

. 2010, 40(1):130-135

Stochastic stability of networked control system with data packet loss and time delay

具有包丢失和时延的网络控制系统的随机稳定性

Yang Li , Guan Xin-ping , Luo Xiao-yuan

杨丽, 关新平, 罗小元

2012

0.0

2013

0.0

2010

0.0

2011

0.0

2011

0.0

2012

0.0

. 2012, 33(2):170-178

The less-conservative robust guaranteed cost fault-tolerant control of networked control systems

少保守性网络化控制系统鲁棒保性能容错控制

Li Wei , Wang Yan-fei.

李炜, 王艳飞

The robust guaranteed cost fault-tolerant control for a networked control system (NCS) with parameter uncertainty was studied. Under the consideration of time-varying delay and packet dropout, the sufficient condition of robust guaranteed cost fault-tolerant control for NCSs against the failure of actuator or sensor was given based on the model with multiple successive delays of state in terms of a delay-dependent approach. The design techniques of optimal guaranteed cost fault-tolerant controller were given by solving the linear matrix inequalities(LMI). Since a lower bound of the time-delay was introduced in the model , the model transformation and the scaling-up of cross terms were not preformed during the proof, and the appropriate free-weighting matrices were introduced, the conservativeness was reduced, and the degree of fault-tolerant satisfaction was improved .Finally, a numerical example was used to illustrate the effectiveness of the proposed method.

研究了一类具有参数不确定性网络化控制系统的鲁棒保性能容错控制问题。同时考虑时变时延和丢包的影响，基于状态多时延模型，推证出了确保闭环系统在执行器或传感器发生失效故障时具有鲁棒保性能容错的时滞依赖充分条件，并以求解线性矩阵不等式(LMIs)的方式给出了最优控制器的设计方法。由于新模型中引入了时延下界，且在证明过程中未进行模型转换和交叉项放大处理，加上适当自由权矩阵的引入，都减少了结果的保守性，提升了容错满意度。最后以一仿真示例验证了文中所述方法的有效性。研究了一类具有参数不确定性网络化控制系统的鲁棒保性能容错控制问题。同时考虑时变时延和丢包的影响，基于状态多时延模型，推证出了确保闭环系统在执行器或传感器发生失效故障时具有鲁棒保性能容错的时滞依赖充分条件，并以求解线性矩阵不等式(LMIs)的方式给出了最优控制器的设计方法。由于新模型中引入了时延下界，且在证明过程中未进行模型转换和交叉项放大处理，加上适当自由权矩阵的引入，都减少了结果的保守性，提升了容错满意度。最后以一仿真示例验证了文中所述方法的有效性。

2012

0.0

2012

0.0

2011

0.0

. 2011, 33(10):2288-2294 DOI:doi:10.3969/j.issn.1001-506X.2011.10.29

Robust guaranteed fault-tolerant design for uncertain NNCS based on T-S model

基于T-S模型的不确定NNCS鲁棒容错保性能设计

Wang Jun , Li Wei , Li Zhan-ming.

王君, 李炜, 李战明

In an uncertain nonlinear networked control system (NNCS) with the influence on network-induced delay and packed dropout, a robust fault-tolerant guaranteed controlled sufficient condition of the system with actuator failures, which is delay-dependent approach, is deduced by constructing an appreciate Lyapunov-Krasovskii functional based on T-S fused model. and the robust fault-tolerant guaranteed control gain can be obtained via an optimization algorithm of solving several linear matrix inequalities (LMIs). This paper considers the lower bound of the time-delay and does not make the model transformation, a less conservative result is obtained. Finally, an example is used to illustrate the effectiveness and feasibility of the proposed approach.

针对一类具有时变时延和丢包的不确定非线性网络化控制系统,基于T-S(Takagi-Sugeno)模糊模型,通过构造适当的Lyapunov-Krasovskii泛函,得出在执行器发生失效故障的情形下,系统基于线性矩阵不等式的渐近稳定且具有良好动态性能的时滞依赖充分条件,并给出了最优鲁棒容错保性能控制器的设计方法。由于证明中没有进行任何模型变换,并考虑了时延下界,使结果具有较少保守性。最后,仿真示例验证了本文所述方法的有效性和可行性。

2013

0.0

2013

0.0

. 2013, 28(12):1874-1883

Non-fragile robust fault-tolerant control for uncertain NCS with actuator saturation

执行器饱和不确定NCS非脆弱鲁棒容错控制

Cao Hui-chao , Li Wei.

曹慧超, 李炜

针对存在时变时延和丢包的不确定网络化控制系统(NCS)，同时考虑执行器饱和、控制器参数摄动以及非线性扰动等约束，研究执行器发生结构性失效故障时系统的鲁棒容错多约束控制问题。基于时滞依赖Lyapunov方法和容错吸引域定义，采用状态反馈控制策略推证出了闭环故障不确定网络化控制系统稳定的少保守性不变集充分条件，并给出了非脆弱鲁棒容错控制器的设计方法以及最大容错吸引域的估计。仿真算例验证了所述方法的可行性和有效性。

2011

0.0

... 近期,一种新的离散事件触发通讯机制^[14](Discrete event-triggered communication scheme,DETCS)被提出,在此机制下,数据传输是根据控制任务按需进行的,相对PTTCS下所有采样数据传输都需通过有限带宽的通信网络实现的NCS来说,信息量按需传输可以更为合理且有效地利用网络资源 ...

2012

0.0

2013

0.0

2007

0.0

. 2007, 24(3):475-479 DOI:doi:10.3969/j.issn.1000-8152.2007.03.028

Feedback stabilization and L2-gain analysis of uncertain systems withstate delay and actuator saturation

含状态时滞及执行器饱和不确定系统反馈镇定及L2增益分析

Wei Ai-rong , Wang Yu-zhen , Zhao Ke-you.

魏爱荣, 王玉振, 赵克友

研究了具有控制饱和状态时滞不确定系统的L2控制问题,提出了状态反馈方法,利用Lyapunov函数可获得时滞相关的线性矩阵不等式.线性矩阵不等式条件可保证闭环系统无干扰时鲁棒内稳定性和在某椭球内预先给定的有干扰时L2性能水平,该不等式通过引入辅助矩阵解除了执行器饱和对系统的影响而更易于实现且减小了保守性.采用线性矩阵不等式技术,将控制器存在的充分条件转化为凸优化问题.在此基础上设计了系统的状态反馈控制器,最后用数值仿真验证了所提出方法的可行性.

... 此外,考虑实际工程中,由于自身物理特性限制和人为界定,执行器饱和问题也常常存在^[17],而且当系统发生故障后,过大的控制量会使执行器更易进入饱和区,因此,基于DETCS,考虑执行器饱和约束和元部件故障,兼顾系统控制性能(Quality of performance,QoP)和网络服务质量(Quality of service,QoS)的NCS容错控制研究更具实际意义和研究价值 ...

2009

0.0

... 注2 与需要通过额外硬件设备对传感器输出量进行连续检测的连续事件触发通讯(Continuous event-triggered communication scheme,CETCS)方式相比^[18],本文所采用的DETCS方式,以一个常采样周期获取系统的状态量,然后利用离散时刻采样点的测量状态计算触发条件,无需关注采样时刻间状态信息的变化,这使得DETCS的实现仅通过一般智能传感器或者软件即可完成,省去了添加硬件的问题 ...

2002

0.0

... 引理1^[19] 给定矩阵K、H#cod#x02208 ...

2011

0.0

... 引理2^[20] 假设f₁,f₂,…,f_N#cod#x02236 ...

... 在推证时,对Lyapunov-Krasovskii泛函导数项的放大处理,本着既尽可能小的放大和不忽略任何有用项,又不增加决策变量、加大计算量的原则,未采用自由权矩阵方法,而是采用了一种性能等价于积分不等式引理且决策变量数少于Jensen积分不等式的互反凸组合引理2^[20] ...

2005

0.0

... 引理3^[21] 任意矩阵N#cod#x02208 ...

1996

0.0

... 引理4^[22] 对于具有适当维数的矩阵Y、M和E,其中Y=Y^T,则: ...