面向可靠感知的传感网节点部署优化算法

引用本文

刘军, 程良伦, 王涛, 王建华. 面向可靠感知的传感网节点部署优化算法. 2015, 45(6): 1941-1945
LIU Jun, CHENG Liang-lun, WANG Tao, WANG Jian-hua. Nodes deployment optimization algorithm for reliable sense in sensor networks. Journal of Jilin University Engineering and Technology Edition, 2015, 45(6): 1941-1945 复制到剪切板

Permissions

面向可靠感知的传感网节点部署优化算法

刘军¹, 程良伦^1,², 王涛¹, 王建华¹

1.广东工业大学自动化学院,广州 510006

2. 广东工业大学计算机学院,广州 510006

作者简介:刘军(1986-),男,博士研究生.研究方向:控制科学与工程,传感器网络,物联网,信息物理融合系统.E-mail:liujun7700@163.com

基金:国家自然科学基金广东联合基金重点项目(U1201251); 广东省自然科学基金研究团队项目(8351009001000002); 广东省自然科学基金博士科研启动项目(S2012040006666)

摘要

首先推导出确定部署时基于V剖分感知误差最小,定义各个节点分区的覆盖权值。然后基于感知节点覆盖权值和虚拟力思想提出了一种部署优化算法,在确保感知不确定性最小化的同时保证网络连通性。最后仿真比较了在不同节点密度以及不同事件优先级下算法的部署性能,结果表明,本文提出的部署算法相比于其他算法能够有效地实现对热点区域的优化部署,保证较小的感知误差。

关键词: 自动控制技术; 移动传感器网络; 事件区域; 覆盖权值

中图分类号:TP393.04 文献标志码:A 文章编号:1671-5497(2015)06-1941-05

Nodes deployment optimization algorithm for reliable sense in sensor networks

LIU Jun¹, CHENG Liang-lun^1,², WANG Tao¹, WANG Jian-hua¹

1.School of Automation,Guangdong University of Technology,Guangzhou 510006, China

2.School of Computer,Guangdong University of Technology,Guangzhou 510006, China

Abstract

In this paper, first, it is deduced that the sensor uncertainty is minimum with Voronoi partition; a node coverage weight by priority function of event area is defined. Then a nodes deployment optimization algorithm is proposed based on node coverage weight and virtual force. It guarantees the connectivity of network while the sensing uncertainty is minimal. Finally, computer simulation is carried to compare the deployability of the proposed algorithm with other algorithms under different node densities and different event priorities. Simulation results show that the proposed deployment algorithm is quick and effective with smaller sensing uncertainty compared with other deployment algorithms. Also the proposed algorithm has strong robustness.

Keyword: automatic control technology; mobile sensor network; event area; coverage weight

Show Figures

0 引言

移动传感器网络(Mobile sensor networks, MSNs)节点具备感知、计算、通信和移动能力, 能够针对部署区域的动态事件进行迅速的部署解决问题^{[1, 2]}。因此MSNs已引起广泛关注。在监测区域内, 针对复杂动态环境, 如何部署移动节点使得MSNs有效地覆盖监测区域或目标是一个重要的研究方向^[3]。

文献[4, 5]借鉴库仑力、胡克定律以及边界斥力等组合虚拟力研究传感器节点在监测区域的三维空间重部署方法, 实现对区域的覆盖以及优化能量效率。Liang等^[6]针对随机部署存在的监测空洞, 通过将多边形分解为三角形后, 提出一种分治部署策略对其实现完全覆盖。涂志亮等^[7]针对动态目标(事件源)的监测优化问题, 集合Voronoi剖分提出基于群集控制的传感器节点部署分布式控制算法。针对移动传感器网络热点覆盖问题, Milan等^[8]提出保证网络连通性是覆盖优化前提, 结合RNG模型保证网络连通性, 提出了热点部署算法能够实现对静态、动态热点的覆盖部署。

有人结合仿生进化算法来研究传感器节点的部署优化, Liu等^[9]通过蚁群三种传输策略提出优化算法, 排除不可行解, 减少搜索空间以完成监测区域的优化覆盖。夏娜等^[10]针对水下传感器网络应用, 提出了一种鱼群启发的水下传感器节点布置算法, 通过模拟鱼群行为, 并结合拥挤度控制, 使节点自主趋向并覆盖事件, 同时实现节点分布密度与事件分布密度相匹配部署。但算法的研究并未考虑网络连通性问题, 作者在进一步研究中, 引入刚性理论构造水下传感器网络覆盖度和连通性的联合优化目标, 提出相应的节点位置评价指标和节点移动策略, 从而较好地解决水下传感器节点自组织布置问题^[11]。

在有些传感器网络应用场景中传感器节点不可能有效覆盖整个目标区域, 比如军事应用监测, 环境监测等大面积部署^{[12, 13]}。以GreenOrbs项目为例^[14], 其1.1 km²面积即部署了1200多个节点, 对于如战场环境面积上千平方公里, 若考虑K-覆盖部署, 其部署的节点数目巨大。在有些应用并不需要对整个区域实时进行有效监测, 只是需要对某些可能出现的目标区域进行有效监控即可。Hamid等^[15]假设监测区域各点的优先级不同, 感知节点异构, 在随机部署后检测自身区域中的空洞大小, 然后提出三种策略移动传感器节点覆盖优先级更高的区域, 算法实现了对优先级区域的覆盖, 但缺少对网络连通性的考虑。

本文假设场景为在大面积区域中, 随机产生部分突发事件, 在监测到事件后, 传感器节点通过移动实现对这些区域的有效覆盖。提出了一种新的分布式部署策略完成对优先级区域的覆盖。该事件是带优先级感知区域, 对其部署需要依据优先级进行部署, 对于优先级高的区域部署的节点应该多, 保证可靠性高; 对于优先级低的区域, 部署的节点可以相对少, 但要求保证网络连通, 这样使得整个网络的部署达到最优。

1 问题模型

假设在传感器网络监测区域中, 某事件随机发生于监测区域中, 如图1所示。其中事件区域依据距离事件中心位置不同而存在不同优先级, 该模型类似于文献[15]。存在优先级函数φ $\begin{matrix} (q) \end{matrix}$ , 表示在点q位置的优先级。若φ $\begin{matrix} (q) \end{matrix}$ > φ $\begin{matrix} (p) \end{matrix}$ , 则表示点q的位置优先级大于点p, 优先级可以表示不同位置信息的重要程度。稀疏部署即在节点数量无法满足完全部署时, 依据不同位置重要程度优化部署节点位置, 使得整体区域的感知数据精度最大化。一般来说, 优先级函数定义为高斯密度函数的形式:φ $\begin{matrix} (q) \end{matrix}$ =ε · exp{-[(x-x₀)²+(y-y₀)²]}, $\begin{matrix} (x, y) \end{matrix}$ 为点p的坐标。φ $\begin{matrix} (q) \end{matrix}$ 可以认为是该处感知信息重要程度或监测事件发生在点q的概率。

	Figure Option View Download New Window
	图1 冗余节点移动Fig.1 Redundant nodes moved

对于感知节点在监测区域部署的优劣可以通过节点对于监测区域中各点的感知误差来衡量。与感知误差为感知节点对分区中某点采集的数据精确程度。与感知误差距离有关, 节点距离目标点越远则误差越大, 误差函数即为区域各点与所述传感器节点的距离的函数。

定义1 误差函数:设p_i为传感器节点S_i在区域A中的位置。感知误差函数为g(‖ q-p_i‖ ), 表示分区中点q被位于位置p_i的节点采集数据的误差。‖ q-p_i‖ 为目标点与感知节点的欧氏距离。

定义2 区域剖分:设n个传感器节点部署在区域A中, 依照各个节点部署位置将整个感知区域分为各个节点的专属区域, 整个分区集合表示为V。V_i代表节点i的感知区域, 其所有剖分的联合构成了整个区域的覆盖。

定义3 节点i的感知区域的误差为:

$\begin{matrix} G_{i} (p_{i}, V_{i}) = \int_{q}^{\in} g (‖ q - p_{i} ‖) dq (1) \end{matrix}$

式中:V_i为节点i的感知区域。

定义4 整个部署区域中的误差函数为:

$\begin{matrix} G (P, V) = \overset{n}{\sum_{i = 1}} \int_{q}^{\in} g (‖ q - p_{i} ‖) dq (2) \end{matrix}$

优化部署就是最小化感知误差函数值。

对于给定的区域A和节点位置部署方案P, 对节点的分区有无限种可能, 依据Voronoi剖分的定义有:

$\begin{matrix} \begin{matrix} V_{i} = {q \in A |‖ q - p_{i} ‖\leq \\ ‖ q - p_{j} ‖, \forall j \neq i} (3) \end{matrix} \end{matrix}$

基于Voronoi剖分的分区是感知误差最小的。但是给定n个传感器节点部署于区域A中, 每一种部署都有一种V剖分, 因此需要寻找优化的部署策略P, 其构成的P能够最小化G $\begin{matrix} (P, V) \end{matrix}$ 。

2 PoI覆盖部署算法

2.1 算法基本思想

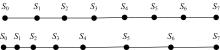
对于有限的传感器节点在带优先级的事件区域内通过算法实现合理的部署, 从而实现对区域的尽可能的精确监测, 而保证连通性是首要条件。主要思想就是通过将事件区域外的节点移动到事件区域中, 并依照各点的优先级进行不同疏密程度的节点覆盖。图1表示如何从事件区域外移动多余的节点到事件区域内的一种推挤策略。由于在事件区域外仅需要保证网络连通性, 因此在保证网络连通性下存在的冗余节点可以通过推挤方法将传感器节点移动到事件区域。这里的思想类似文献[16], 使得保证网络连通性的传感器节点最小化, 使得保证监测区域的传感器节点数量最大化。

如何实现在事件区域内形成这种疏密部署是算法要解决的另外一个问题。一个剖分区域的优先级通过覆盖权值来衡量, 如定义5所示。

定义5 覆盖权值:

$\begin{matrix} α_{Π_{i}} = \int_{Π_{i}} φ (q) dq (4) \end{matrix}$

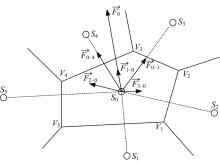
式中:Π _i表示第i节点的分区; $\begin{matrix} α_{Π_{i}} \end{matrix}$ 为节点自身区域的覆盖权值。

本文拟采用一种虚拟力策略实现节点移动, 假设传感器节点受到周围邻居节点的引力或斥力。每个节点在自己的监测区域中能够得出一个权值, 即优先级与区域积分, 定义为覆盖权重值。若本节点的覆盖权值大, 则对周围其他节点有引力, 使得周围节点靠近, 自身的区域减少, 而自身覆盖权重值则降低, 最终目标使得整个网络节点的覆盖权重值一致。

如图2所示, 节点S₀与S₁, S₂, S₃, S₄, S₅相邻。各节点的覆盖权值分别为: $\begin{matrix} α_{Π_{0}} \end{matrix}$ =10, $\begin{matrix} α_{Π_{1}} \end{matrix}$ =6, $\begin{matrix} α_{Π_{2}} \end{matrix}$ =8, $\begin{matrix} α_{Π_{3}} \end{matrix}$ =16, $\begin{matrix} α_{Π_{4}} \end{matrix}$ =18, $\begin{matrix} α_{Π_{5}} \end{matrix}$ =5。节点S₀受到周围节点的引力或斥力, 其中S₃, S₄覆盖权重大于S₀, 则为引力 $\begin{matrix} {\vec{F}}_{0 - 4} \end{matrix}$ , $\begin{matrix} {\vec{F}}_{0 - 3} \end{matrix}$ , 另外则为斥力 $\begin{matrix} {\vec{F}}_{2 - 0} \end{matrix}$ , $\begin{matrix} {\vec{F}}_{1 - 0} \end{matrix}$ , $\begin{matrix} {\vec{F}}_{5 - 0} \end{matrix}$ , 其5个力合成为合力 $\begin{matrix} {\vec{F}}_{0} \end{matrix}$ , 如图2所示。

	Figure Option View Download New Window
	图2 节点受力分析Fig.2 Nodes stress analysis

保证在事件区域内的各个节点覆盖权重值一致, 在外围由于优先级低, 要保证权值一致则节点分区大; 在中央位置优先级高, 当权值一致则分区小, 从而使得节点形成疏密明显的非均匀部署。

2.2 算法实现

算法分为4步:①节点向周围节点广播自身位置, 然后构建自身V剖分; ②每个节点通过特定部署策略计算新的位置, 周围信息计算目标点, 得出新的部署策略; ③若本地与邻居节点权值比较其小于阈值则不移动; ④反复迭代, 直到任意一个节点的权值与周围节点的权值之差小于阈值, 则停止移动。

算法分为3部分:①计算虚拟力; ②计算方向和距离; ③节点移动。传感器节点向周围节点广播自身位置后, 进行V-剖分, 运行部署算法。感知节点u计算自身合力, 然后计算方向和距离, 最后移动, 移动时需考虑RNG图, 保证网络连通。

在移动时必须考虑连通性。d⁺(u)表示感知节点u到它的最远RNG节点的距离; R为节点通信距离, d为节点运行算法后的移动距离。d有如下约束条件:①d≤ (R-d⁺(u))/2; ②若d< σ ₀, 则d=0, 即移动距离d应小于通信距离与最远邻居节点距离之差的一半, 最小移动距离应小于最小门限值ε ₁。条件①和②给出了移动距离上限和下限的约束。条件①为节点最大移动距离约束, 移动距离d应小于通信距离与最远邻居节点距离之差的一半, 条件②保证最小移动距离应小于最小门限值σ ₀。条件①主要保证网络的连通性, 条件②主要为保证节点移动收敛。

3 仿真试验

3.1 试验条件

在Matlab2010平台上测试部署算法性能, 主要通过比较优化部署后的整个网络的感知误差值、收敛速度来判断部署算法性能。在仿真试验中, 节点随机部署在区域面积为100 m× 100 m的监测区域, 通过运行算法后实现疏密部署效果。监测事件随机产生于监测区域某一位置, 其他参数如表1所示。

表1 参数设置 Table 1 Parameter settings

试验	(x_p, y_p)	R(m)	σ ₀(m)	N	ε	g $\begin{matrix} (‖ q - p_{i} ‖) \end{matrix}$
1	p(29, 31)	25	0.5	20	0.1	$\begin{matrix} \frac{0.5‖ q - p_{i} ‖^{2}}{1 + R^{2}} \end{matrix}$
2	p(29, 31)	25	0.5	20	0.01
3	p(29, 31)	25	0.5	50	0.1

表1 参数设置 Table 1 Parameter settings

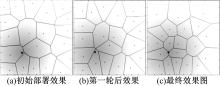
表1中, x_p和y_p分别是节点的横、纵坐标; R为节点通信半径; ε 为事件优先级因子, 表示事件概率收敛程度; σ ₀表示最小移动距离; g $\begin{matrix} (‖ q - p_{i} ‖) \end{matrix}$ 为节点误差函数。仿真测试运行于IBM Think Centre M8500t, 4核3.2 GHz, 4 G内存。

3.2 试验分析

图3为试验1的部署效果图, 其中黑点代表事件中心区域, 节点通过运行部署算法, 慢慢向事件中心聚集, 最终达到疏密部署的效果。

	Figure Option View Download New Window
	图3 优先级事件区域部署效果图Fig.3 Deployment in priority event area

由图4可以看出, 算法经过多轮运行, 最后传感器节点部署完毕, 形成了依据优先级区别的疏密部署效果。由图4还可以看出, 在事件区域外围, 优先级低, 节点较稀疏, 各个节点对应的监测剖分区域面积较大; 事件中心区域优先级较高, 节点部署较稠密, 对应的监测剖分区域面积较小, 并通过RNG图保证了节点的连通性。

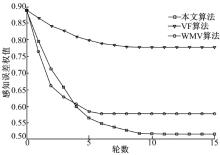
	Figure Option View Download New Window
	图4 不同算法在运行时误差权值比较Fig.4 Error weights in rounds with different algorithms

通过仿真比较与其类似的优先级区域的移动传感器节点部署算法性能。一种为基于经典虚拟力的均匀部署, 一种为MWV针对优先级区域的部署^[15], 由于这些算法的假设条件和运用场景与本文并不太一致, 下面做简单仿真比较。图4为各轮运行时误差值变化。图5为在不同的事件优先级情形下, 其误差函数值对比。

	Figure Option View Download New Window
	图5 不同节点密度以及事件优先级下误差权值比较Fig.5 Error weights comparison with different node density and events priority

从图4和图5中可以看出, 本文提出的算法在运行15轮后其误差值最小, 说明其部署的性能优于其他两种算法。另外可以看出:本文算法的收敛性不如MWV算法, 主要因为本文提出计算权值方法以及合力方法较该算法的法则复杂。另外算法比较了在不同节点密度下以及在不同的时间优先级下的误差权值, 可以看出节点数量的部署性能更加优异, 另外在高事件优先级下本文算法的性能更佳, 这是由于本文设计的出发点就是为了满足权值一致。

4 结束语

针对带优先级的事件区域的监测研究传感器节点优化部署问题, 建立数学模型, 结合Voronoi图、RNG图以及虚拟力思想实现保证感知节点的连通性情况下优化部署性能, 降低感知误差。试验结论反应本文提出的方法针对优先级区域实现了疏密部署, 而且相比于同类算法, 具有更小的感知误差。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Chen A, Li Z Z, Lai T H, et al. One-way barrier coverage with wireless sensors[C]∥IEEE INFOCOM 2011 Mini-Conference, Shanghai, China, 2011: 626-630. [本文引用:1]
[2]	He S, Chen J, Li X, et al. Cost-effective barrier coverage by mobile sensor networks[C]∥2012 IEEE Proceedings INFOCOM, Orland o, USA, 2012: 819-827. [本文引用:1]
[3]	Cortés J, Martínez S, Karatas T, et al. Coverage control for mobile sensing networks[J]. IEEE Transactions on Robotics and Automation, 2004, 20(2): 243-255. [本文引用:1]
[4]	刘惠, 柴志杰, 杜军朝, 等. 基于组合虚拟力的传感器网络三维空间重部署算法研究[J]. 自动化学报, 2011, 37(6): 713-723. Liu Hui, Chai Zhi-jie, Du Jun-zhao, et al. Sensor re-deployment algorithm based on combined virtual forces in three dimensional space[J]. Acta Automatica Sinica, 2011, 37(6): 713-723. [本文引用:1]
[5]	Wang Xue, Wang Sheng. Hierarchical deployment optimization for wireless sensor networks[J]. IEEE Transactions on Mobile Computing, 2011, 10(7): 1028-1041. [本文引用:1]
[6]	Liang C S, Chao Y Le, Chu S Y. The divide-and -conquer deployment algorithm based on triangles for wireless sensor networks[J]. IEEE Sensors Journal, 2011, 11(3): 781-790. [本文引用:1]
[7]	涂志亮, 王强, 沈毅. 移动传感器网络中目标跟踪与监测的同步优化[J]. 自动化学报, 2012, 38(3): 452-461. Tu Zhi-liang, Wang Qiang, Shen Yi. A distributed simultaneous optimization algorithm for tracking and monitoring of moving target in mobile sensor network[J]. Acta Automatica Sinica, 2012, 38(3): 452-461. [本文引用:1]
[8]	Erdelj M, Razafindralambo T, Simplot-Ryl D. Covering points of interest with mobile sensors[J]. IEEE Transactions on Pallel and Distributed Systems, 2013, 24(1): 32-43. [本文引用:1]
[9]	Liu Xu-xun. Sensor deployment of wireless sensor networks based on ant colony optimization with three classes of ant transitions[J]. IEEE Communications Letters, 2012, 16(10): 1604-1607. [本文引用:1]
[10]	夏娜, 王长生, 郑榕, 等. 鱼群启发的水下传感器节点布置[J]. 自动化学报, 2012, 38(2): 295-302. Xia Na, Wang Chang-sheng, Zheng Rong, et al. Fish swarm inspired underwater sensor deployment[J]. Acta Automatica Sinica, 2012, 38(2): 295-302. [本文引用:1]
[11]	夏娜, 郑语晨, 杜华争, 等. 刚性驱动水下传感器节点自组织布置[J]. 计算机学报, 2013, 36(3): 494-505. Xia Na, Zheng Yu-chen, Du Hua-zheng, et al. Rigidity driven underwater sensor self-organized deployment[J]. Chinese Journal of Computers, 2013, 36(3): 494-505. [本文引用:1]
[12]	Pompili D, Melodia T, Akyildiz I F. Distributed routing algorithms for underwater acoustic sensor networks[J]. IEEE Transactions on Wireless Communications, 2010, 9(9): 2934-2944. [本文引用:1]
[13]	Mao Xu-fei, Miao Xin, He Yuan, et al. CitySee: urban CO₂ monitoring with sensors[C]∥2012 Proceedings IEEE INFOCOM, Orland o, FL, USA, 2012: 1611-1619. [本文引用:1]
[14]	Liu Y, He Y, Li M, et al. Does wireless sensor network scale? A measurement study on GreenOrbs[J]. IEEE Transactions on Parallel and Distributed Systems, 2013, 24(10): 1983-1993. [本文引用:1]
[15]	Mahboubi H, Habibi J, Aghdam A G, et al. Distributed deployment strategies for improved coverage in a network of mobile sensors with prioritized sensing field[J]. IEEE Transactions on Indusrial Informatics, 2013, 9(1): 451-461. [本文引用:2]
[16]	Wang G L, Cao G H, Porta T F L. Movement-assisted sensor deployment[J]. IEEE Transactions on Mobile Computing, 2006, 5(6): 640-652. [本文引用:1]

2011

0.0

... 0 引言移动传感器网络(Mobile sensor networks,MSNs)节点具备感知、计算、通信和移动能力,能够针对部署区域的动态事件进行迅速的部署解决问题^[1,2] ...

2012

0.0

... 0 引言移动传感器网络(Mobile sensor networks,MSNs)节点具备感知、计算、通信和移动能力,能够针对部署区域的动态事件进行迅速的部署解决问题^[1,2] ...

2004

0.0

... 在监测区域内,针对复杂动态环境,如何部署移动节点使得MSNs有效地覆盖监测区域或目标是一个重要的研究方向^[3] ...

2011

0.0

. 2011, 37(6):713-723 DOI:10.3724/SP.J.1004.2011.00713

Sensor re-deployment algorithm based on combined virtual forces in three dimensional space

基于组合虚拟力的传感器网络三维空间重部署算法研究

Liu Hui , Chai Zhi-jie , Du Jun-zhao

刘惠, 柴志杰, 杜军朝

1. Software Engineering Institute, Xidian University, Xi'an 710071; 2. Software School, Xidian University, Xi'an 710071; 3. State Key Laboratory of ISN, Xidian University, Xi'an 710071

The sensor redeployment problem is an important problem to improve sensor coverage in wireless sensor networks. A practical algorithm should consider the limitation of the sensor resources and the situation of the deployment. A distributed algorithm based on the combined virtual forces is designed in this paper. In this algorithm, the repulsive force from the 1-hop neighbors based on Coulomb's law, the attractive force from the sensing region center, and the repulsive force from the boundaries based on Hook's law are defined. Then the sensor position adjustment in one step is calculated by combining these forces mentioned above with the energy consumption factors. Meanwhile, the termination condition is also given in this algorithm to ensure the sensors can be redeployed to proper positions. Theoretical analysis and simulation results show that all of the sensors which are deployed in a random way will move into sensing region and self-organize a high-coverage and bi-connected network topology with low energy consumption. The obstacle problem can also be handled in this paper.

无线传感器网络(Wireless sensor networks, WSNs)的重部署问题是提高无线传感器网络覆盖性能的一个重要问题, 实用化的重部署算法需要充分考虑传感器资源的有限性和实际布撒情况. 本文设计了基于组合虚拟力的分布式算法,该算法定义了传感器受到的邻居节点间的基于库仑力的斥力、目标覆盖区域的基于胡克定律的中心吸引力和边界斥力, 综合这些力的合力以及单位能耗因素求得传感器节点每次移动的目标位置. 本文算法还给出了调整的终止条件以保证传感器能够重部署至合理位置. 理论论证和仿真实验表明,提出的基于组合虚拟力的重部署算法能使所有随机布撒的传感器节点在低能耗的情况下, 进入目标覆盖区域并在该区域内自组织成一个具有高覆盖性和重连通性的网络拓扑. 本文算法还解决了覆盖区域中存在障碍物的复杂情况.

2011

0.0

2011

0.0

... Liang等^[6]针对随机部署存在的监测空洞,通过将多边形分解为三角形后,提出一种分治部署策略对其实现完全覆盖 ...

2012

0.0

. 2012, 38(3):452-461 DOI:10.3724/SP.J.1004.2012.00452

A distributed simultaneous optimization algorithm for tracking and monitoring of moving target in mobile sensor network

移动传感器网络中目标跟踪与监测的同步优化

Tu Zhi-liang , Wang Qiang , Shen Yi.

涂志亮, 王强, 沈毅

Department of Control Science and Engineering, Harbin Institute of Technology, Harbin 150001

To improve the quality of coverage for monitoring a moving target (event) in mobile sensor networks (MSNs), this paper first formulates a monitoring evaluation criterion based on Voronoi partition, then proposes a distributed flocking based control algorithm. This paper adopts an algorithm which combines the least square method with the consensus algorithm to estimate the relative position of the target. Compared to traditional methods, only local and 1-hop neighborhood (measurable) information is required, hence it reduces the communication time and energy consumption. While optimizing the quality of monitoring (QoM), it also regulates all sensors' velocities to the target velocity, hence the topology of the network is kept better and the total energy consumption on movement of sensors is reduced. With the assumption that the target is moving at a constant velocity or its acceleration is available all sensors, the velocities of all sensors would be asymptotically aligned with the target velocity and QoM would converge to a local maximum. The estimation algorithm for the relative position to the target is simple and effective.

针对移动传感器网络(Mobile sensor networks, MSNs)中动态目标(事件源)的监测优化问题, 为提高网络覆盖质量, 建立基于Voronoi剖分的监测性能(Quality of monitoring, QoM)评价函数, 提出基于群集控制的传感器节点部署分布式控制算法. 每个节点在本地结合最小二乘法和一致性算法来估计目标相对位置. 相比传统算法, 本文算法只需本地和单跳通信(可观测)邻居的信息, 从而减小通信时长和能耗. 算法在提高以目标为中心的一定区域监测性能的同时, 使全体传感器速度趋于一致, 从而在尽量保持网络拓扑结构的同时减少了整体移动能耗. 在目标匀速或目标加速度信息全网可知的情况下, 全体传感器速度渐近收敛至目标速度, 且监测性能收敛至局部最优. 所采用的目标位置估计滤波算法计算简单、切实可行.

... 涂志亮等^[7]针对动态目标(事件源)的监测优化问题,集合Voronoi剖分提出基于群集控制的传感器节点部署分布式控制算法 ...

2013

0.0

... 针对移动传感器网络热点覆盖问题,Milan等^[8]提出保证网络连通性是覆盖优化前提,结合RNG模型保证网络连通性,提出了热点部署算法能够实现对静态、动态热点的覆盖部署 ...

2012

0.0

... 有人结合仿生进化算法来研究传感器节点的部署优化,Liu等^[9]通过蚁群三种传输策略提出优化算法,排除不可行解,减少搜索空间以完成监测区域的优化覆盖 ...

2012

0.0

. 2012, 38(2):295-302 DOI:10.3724/SP.J.1004.2012.00295

Fish swarm inspired underwater sensor deployment

鱼群启发的水下传感器节点布置

Xia Na , Wang Chang-sheng , Zheng Rong

夏娜, 王长生, 郑榕

1. School of Computer and Information, Hefei University of Technology, Hefei 230009, P.R. China; 2. Engineering Research Center of Safety Critical Industrial Measurement and Control Technology, Hefei 230009, P.R. China; 3. Department of Computer Science, University of Houston, Houston 77204, USA

Underwater sensor networks (UWSNs) can be applied to sea resources reconnaissance, pollution monitoring, assistant navigation, etc., and they have become a hot field in wireless sensor networks. In open and complicated underwater environments, the monitored target is dynamic and uncertain. It is a key topic for sensors to adjust their positions according to the environment and targets, so as to cover the targets in an optimal manner. This paper defines the underwater sensor deployment problem and its performance evaluation metrics, and then presents a fish swarm inspired sensor deployment algorithm. Simulating the behavior of fish swarm and taking the crowd factor into account, the method can drive the sensors to cover almost all the events, and make the sensors density match the events density. Through extensive comparative simulations, we demonstrate that the proposed algorithm can solve the underwater sensor deployment problem effectively and it is be simple, fast in convergence, and realizable in distributed manner.

水下传感器网络(Underwater sensor networks, UWSNs)可用于海洋资源勘测、污染监控和辅助导航等领域, 已成为无线传感器网络方向的研究热点. 在开放式复杂的水下环境中监测目标具有高动态和不确定的特点, 节点如何根据环境和目标的变化自主调整位置, 以达到对监测目标的优化覆盖是一个关键问题. 本文描述了水下传感器节点布置问题, 定义了性能评价指标"事件集覆盖效能", 并提出了一种鱼群启发的水下传感器节点布置算法, 通过模拟鱼群行为, 并结合拥挤度控制, 使节点自主趋向并覆盖事件, 同时实现节点分布密度与事件分布密度相匹配. 大量对比仿真实验结果表明该算法可以有效解决水下传感器节点布置问题, 并具有复杂度低、计算量小、收敛速度快和分布式可实现的优点.

... 夏娜等^[10]针对水下传感器网络应用,提出了一种鱼群启发的水下传感器节点布置算法,通过模拟鱼群行为,并结合拥挤度控制,使节点自主趋向并覆盖事件,同时实现节点分布密度与事件分布密度相匹配部署 ...

2013

0.0

... 但算法的研究并未考虑网络连通性问题,作者在进一步研究中,引入刚性理论构造水下传感器网络覆盖度和连通性的联合优化目标,提出相应的节点位置评价指标和节点移动策略,从而较好地解决水下传感器节点自组织布置问题^[11] ...

2010

0.0

... 在有些传感器网络应用场景中传感器节点不可能有效覆盖整个目标区域,比如军事应用监测,环境监测等大面积部署^[12,13] ...

2012

0.0

... 在有些传感器网络应用场景中传感器节点不可能有效覆盖整个目标区域,比如军事应用监测,环境监测等大面积部署^[12,13] ...

2013

0.0

... 以GreenOrbs项目为例^[14],其1 ...

2013

0.0

... Hamid等^[15]假设监测区域各点的优先级不同,感知节点异构,在随机部署后检测自身区域中的空洞大小,然后提出三种策略移动传感器节点覆盖优先级更高的区域,算法实现了对优先级区域的覆盖,但缺少对网络连通性的考虑 ...

... 一种为基于经典虚拟力的均匀部署,一种为MWV针对优先级区域的部署^[15],由于这些算法的假设条件和运用场景与本文并不太一致,下面做简单仿真比较 ...

2006

0.0