多角度特征融合的视频人脸纹理表示及识别

引用本文

王玉, 申铉京, 陈海鹏, 谭颖. 多角度特征融合的视频人脸纹理表示及识别. 2015, 45(6): 1954-1960
WANG Yu, SHEN Xuan-jing, CHEN Hai-peng, TAN Ying. Video-based face texture representation and recognition with fusion features from multi-view. Journal of Jilin University Engineering and Technology Edition, 2015, 45(6): 1954-1960 复制到剪切板

Permissions

多角度特征融合的视频人脸纹理表示及识别

王玉^1,^2,³, 申铉京^1,², 陈海鹏^1,², 谭颖⁴

1.吉林大学计算机科学与技术学院,长春 130012

2.吉林大学符号计算与知识工程教育部重点实验室,长春 130012

3.吉林大学应用技术学院,长春 130012

4.吉林大学公共计算机教学与研究中心,长春 130012

陈海鹏(1978-),男,副教授,博士.研究方向:图像处理与模式识别,多媒体信息安全.E-mail:chenhp@jlu.edu.cn

作者简介:王玉(1983-),男,讲师,博士研究生.研究方向:图像处理与模式识别,多媒体信息技术.E-mail:wangyu001@jlu.edu.cn

基金:国家青年科学基金项目(61305046); 吉林省自然科学基金项目(20140101193JC); 吉林省青年科学基金项目(20130522117JH)

摘要

提出了一种在Gabor变换幅值域内提取3个正交平面上的局部二值模式的多角度特征融合的视频人脸纹理表示及其识别方法。首先对视频帧集合中归一化的每幅人脸图像进行不同尺度和方向的Gabor小波变换得到增强的Gabor幅值图谱。然后采用3个正交平面上的局部二值模式提取视频纹理特征。最后采用基于Fisher加权的Chi平方概率统计最近邻方法进行视觉人脸识别。通过在Honda/UCSD视频库进行的相关实验,验证了算法的有效性,该方法对光照变化、表情变化等具有较好的鲁棒性。

关键词: 计算机应用; 视频人脸识别; Gabor滤波器; 三个正交平面上的局部二值模式; Fisher准则

中图分类号:TP391 文献标志码:A 文章编号:1671-5497(2015)06-1954-07

Video-based face texture representation and recognition with fusion features from multi-view

WANG Yu^1,^2,³, SHEN Xuan-jing^1,², CHEN Hai-peng^1,², TAN Ying⁴

1.College of Computer Science and Technology, Jilin University, Changchun, Jilin 130012, China

2.Key Laboratory of Symbolic Computation and Knowledge Engineering of Ministry of Education, Jilin University, Changchun, Jilin 130012, China

3.Applied Technology College Jilin University, Changchun 130012, China

4.Center for Computer Fundamental Education of Jilin University,Changchun 130012,China

Abstract

A video-based face texture program was proposed, which can extract binary patterns from three orthogonal planes in the frequency domain of the Gabor transform (GLBP-TOP). First, each normalized face was transformed by Gabor wavelet to get enhanced Gabor magnitude map. Then, the LBP-TOP operator was applied to the maps to extract video texture. Finally, weighted Chi square statistics based on Fisher Criterion were used to realize the face classification. The proposed algorithm achieved good results in the Honda-UCSD database, and was effective and robust under changes of illustration and expressions.

Keyword: computer application; video-based face recognition; Gabor filters; local binary patterns from three orthogonal planes (LBP-TOP); Fisher criterion

Show Figures

0 引言

视频人脸识别技术近年来成为计算机视觉领域的研究热点和难点, 伴随着物联网、网络安全等的发展, 具有广阔的应用前景。相对于静态图像, 动态视频中可选用的特征信息更加丰富多样^[1], 例如, 视频的时间动态信息有助于识别率的提升; 从视频序列中可以选取分辨率相对较高的图像以提高识别性能; 还可以通过视频学习重构目标三维模型, 利用这些模型可以高效地实现目标识别。总之, 时间和运动信息在基于视频的目标识别中具有重要作用。

视频人脸识别方法主要分为两类:一类是设法提取出视频序列中最具代表性的单独人脸帧图像, 采用传统的基于静态图像的人脸识别方法^{[2, 3]}, 包括基于几何特征的方法、基于统计的方法等对人脸进行识别。该类方法存在的主要问题是对关键帧的定义较为模糊, 且没有有效利用视频中的上下文信息。另外一类就是将视频看成是一个视频帧集合^{[4, 5]}, 从帧集合的角度进行分析, 利用3D建模、时空连续信息的概率模型、设计视频纹理描述等方法提高识别率, 在这类方法中如何充分利用视频中人脸的时间和空间信息克服视频中人脸分辨率低, 光照、表情、姿态变化剧烈等困难是研究的重点。

本文从帧集合的角度出发, 针对如何在低计算复杂度的前提下能够有效表示视频人脸纹理并进行识别的问题提出了一种基于三个正交平面上的Gabor局部二值模式空间的人脸纹理描述及相应的识别方法。实验结果表明:与传统的从图像的灰度空间统计得到的LBP-TOP特征直方图相比, 本文算法通过结合Gabor变换和LBP-TOP算子的独特优势提取出了多角度特征融合的视频人脸纹理特征, 从而有效地增强了特征直方图的表示能力。同时, 本文算法对光照变化、表情变化是鲁棒的, 而且具备较强的可判别能力。

1 算法框架

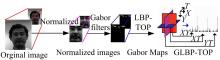
本文提出了多角度特征融合的基于GLBP-TOP的视频人脸纹理表示和识别方法, 该方法首先利用Gabor变换对视频序列中选取出的每个单帧图像提取多方向、多尺度的局部频域特征; 然后通过LBP-TOP算子对这些特征进行编码后统计得到的特征直方图来表示视频纹理, 人脸的分类识别则可以通过特征直方图的匹配来实现。在此基础上, 本文还采用了Fisher准则对人脸不同区域进行统计, 得到权重信息, 以实现加权的直方图匹配策略, 进一步提高了识别精度。算法框架如图1所示, 算法主要步骤如下:

	Figure Option View Download New Window
	图1 本文算法框架Fig.1 Framework of the proposed method

(1)以双眼坐标为基准对从视频中提取的人脸视频序列进行人脸归一化处理。

(2)在预处理阶段, 对人脸视频序列中的每个视频帧进行两个尺度、四个方向的Gabor变换, 得到频域幅值图像, 并对获得的多幅图像进行整合以增强图像幅值特征, 目的就是提取出人脸视频帧中的频域信息。

(3)对Gabor幅值图像集合划分块, 并对每个分块提取LBP-TOP视频纹理特征, 获得每个分块级的局部直方图统计信息, 以获得视频人脸的局部时域-空域纹理信息。

(4)将各个分块级的LBP-TOP特征直方图进行级联操作, 构成整个视频序列的全局直方图, 从而获得视频人脸的多角度特征融合的纹理表示特征。

(5)在分类识别阶段, 采用Chi平方概率统计的最近邻方法, 对待检测的视频人脸序列特征直方图和样本集中的已知人脸特征直方图进行相似性判定, 相对于各分块权重相同的匹配策略, 本文采用基于Fisher准则的加权Chi平方概率统计的识别方法来提高识别精度, 并通过相关的对比实验验证了本文算法的有效性。

2 视频人脸纹理表示

通过结合频率域、空间域和时间域中人脸表示的优势, 设计并实现多特征融合的视频人脸纹理表示方法必然会提高视频人脸识别精度。

2.1 增强的Gabor幅值图谱

Gabor小波变换能够提取图像的多尺度、多方向局部频率信息, 可以增强一些关键特征, 在提取目标的局部空间频率域信息方面具有良好的特性。在人脸识别领域中, Gabor变换得到了广泛的应用, 如基于Gabor特征的Fisher判别人脸识别^[6]等。

二维Gabor小波函数定义为:

$\begin{matrix} \begin{matrix} ψ_{μ, ν} (z) = \frac{‖ k_{μ, ν} ‖^{2}}{σ^{2}} \exp (- \frac{‖ k_{μ, ν} ‖^{2} ‖ z ‖^{2}}{2 σ^{2}}) \cdot \\ [\exp (i k_{μ, ν} z) - \exp (- \frac{σ^{2}}{2})] (1) \end{matrix} \end{matrix}$

式中:μ 、ν 分别为Gabor核的方向和尺度; z=(x, y)代表图像中的一个像素点; k_μ_,_ν控制高斯窗口的宽度、震荡部分的波长及方向, ν 的取值决定了Gabor滤波的波长, μ 的取值表示Gabor核的方向。

Gabor人脸可以通过二维Gabor小波函数和人脸图像进行卷积运算得到:

$\begin{matrix} G_{ψ, f} (x, y) = f (x, y) * ψ (z) (2) \end{matrix}$

Gabor小波函数与图像的卷积结果是由实部和虚部两个分量构成的复数响应(滤波系数)。幅值比较稳定, 不会随位置产生旋转, 幅值信息反映了图像的能量谱, 因此常被用来进行人脸的特征表示。其幅值表示为:

$\begin{matrix} M (x, y) = \sqrt{[Re (G {(x, y))]}^{2} + [Im (G {(x, y))]}^{2}} (3) \end{matrix}$

式中:Re(G(x, y))、Im(G(x, y))分别为G(x, y)的实部和虚部。

这里取m∈ {0, 1}两个尺度, n∈ {0, 1, 2, 3}四个方向的幅值图谱, 并通过如下方法获得增强的Gabor幅值图谱表示:

$\begin{matrix} E (x, y) = {[\overset{1}{\sum_{m = 0}} \overset{3}{\sum_{n = 0}} M_{mn}^{2} (x, y)]}^{\frac{1}{2}} (4) \end{matrix}$

2.2 三个正交平面上的局部二值模式

LBP算子于1996年由Ojala等提出^{[7, 8]}, 是一种从纹理局部近邻定义中衍生出来在灰度范围内的纹理度量算子。该算子具有很强的分类能力、较高的计算效率、灰度不变性和旋转不变性的特点。LBP算子计算过程为:定义一个3× 3的窗口, 以窗口中心点灰度值为阈值, 对相邻点的灰度作二值化处理, 然后按顺时针方向将这些值进行加权求和, 得到该窗口中心点的LBP编码值, 计算过程如图2所示。

	Figure Option View Download New Window
	图2 LBP描述符表示方法Fig.2 Basic LBP descriptor

对于给定图像中的任一像素点, 其LBP编码值可通过如下公式计算得到:

$\begin{matrix} LB P_{P, R} (x_{c}, y_{c}) = \overset{P - 1}{\sum_{p = 0}} 2^{p} s (I_{p} - I_{c}) (5) \end{matrix}$

式中:s(x)= $\begin{matrix} \{\begin{matrix} 1, & if x \geq 0 \\ 0, & else \end{matrix} \end{matrix}$ ; I_c表示当前像素点的灰度; I_p表示当前像素点的邻域像素的灰度; P表示邻域像素的个数; R表示邻域的圆周半径。

采用双线性插值来计算邻域不在图像网格上的像素点的灰度值。当图像中的每个像素点都统计得到LBP编码值后, 可以建立一个统计直方图用于表示图像的纹理。

通过LBP算子实现人脸纹理描述的基本思想是:将正规化后的正面人脸图像进行若干分块划分操作, 对各分块利用LBP算子构建局部的人脸纹理描述特征直方图, 然后通过把各局部纹理表示级联组合形成全局纹理表示, 从而得到人脸图像空间域上的纹理特征直方图。

人脸识别过程中, 光照变化对识别率的影响很大, 从图3和LBP算子的计算公式(式(5))可以看出, LBP算子具有灰度平移不变性, 即LBP算子对均匀光照变化是鲁棒的。从而, 以LBP算子为基础衍生出的其他算子也都满足这样的特性, 比如描述视频纹理的VLBP算子和LBP-TOP算子。

	Figure Option View Download New Window
	图3 LBP算子的灰度平移不变性Fig.3 Gray scale invariance of LBP descriptor

动态局部二进制模式(VLBP)是在LBP的基础上加入运动特征形成的。VLBP算子提取的是图像中的纹理特征和运动特征, 可用于图像序列的人脸识别。VLBP算子的提取公式为:

$\begin{matrix} VLB P_{L, P, R} (x, y, t) = \overset{3 P + 1}{\sum_{p = 0}} 2^{p} s (I_{p} - I_{c}) (6) \end{matrix}$

在标准的VLBP算子计算中, 不仅包括了当前帧的P个邻域像素, 同时包括了时间间隔为L的前后两帧的P+1个邻域像素, 共计3P+2个邻域像素。参数P决定了特征向量的大小, 当P较小时, 特征直方图维度较低, 同时意味着丢失更多的细致纹理信息; 而当P较大时, VLBP算子二进制位将迅速增加, 直接导致最终得到的统计直方图维度较高, 一定程度上限制了VLBP算子的应用。为了解决上述问题, 提出了LBP-TOP^[9]算子, 并在此基础上衍生出多种纹理表示算法^[10]。

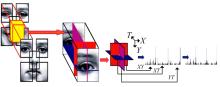
一个视频序列可以被认为是以时间轴T为中心的XY面的堆叠, 但却忽视了视频序列也可以是以Y轴为中心的XT面的堆叠, 或是以X轴为中心的YT面的堆叠。XT平面和YT平面同样提供了关于时空过渡的大量信息。LBP-TOP算子就是在XY、XT和YT三个正交面上提取级联LBP特征, 统计得到这三个方向上的纹理变化信息。由此, 视频序列在三个方向上的运动和表现信息就都得到了表示, 这其中包括了空间域信息(XY-LBP)和时间-空间域信息(XT-LBP和YT-LBP), 同时, LBP-TOP算子相对于VLBP算子, 在每帧考虑P个邻域的情况下, 可以将直方图维度从2³^P+²降至3× 2^P, 降低了计算的时间复杂度。基于分块级的LBP-TOP算子描述过程如图4所示。

	Figure Option View Download New Window
	图4 通过级联直方图表示时空连续性纹理特征Fig.4 Spatiotemporal texture feature represented by cascading LBP-TOP histograms

3 视频人脸识别方法

3.1 加权的Chi平方概率统计

本文采用Chi平方概率统计来度量两个直方图序列之间的相似度。Chi平方概率统计计算公式为:

$\begin{matrix} χ^{2} (S, M) = \overset{l}{\sum_{i}} \frac{(S_{i} - M_{i})^{2}}{S_{i} + M_{i}} (7) \end{matrix}$

式中:S、M表示被比较的两个直方图序列; l代表直方图的维度。

按照式(7)可以计算出待检测人脸序列S与每个样本序列M之间的距离, 并通过最近邻分类器(kNN)将S归为距离最小的一类。

构成GLBP-TOP的每个分块级特征直方图对应的是人脸不同区域的纹理变换, 而不同区域的可辨别能力显然应该是不同的, 对人脸的不同区域赋予不同的权值可以反映各个区域的变化规律, 将有效提高识别能力, 则加权相似度计算公式可重写为式(8)的形式:

$\begin{matrix} χ_{w}^{2} (S, M) = \sum_{i, j} w_{j} \frac{(S_{i, j} - M_{i, j})^{2}}{S_{i, j} + M_{i, j}} (8) \end{matrix}$

式中:w_j为全局特征直方图的第j个分块的权值。

3.2 基于Fisher准则的人脸识别

本文采用基于Fisher准则统计加权的Chi平方概率统计匹配策略, 通过对人脸不同区域特征直方图赋予相应的权重信息来提高识别的精度。Fisher准则^[11]的基本思想是通过使类内散度尽可能小, 而类间散度尽可能大来分析每个区域的权值, 用于评估不同人脸区域的辨别能力, 该准则已经得到广泛的应用。对于C个类的分类问题, 同类样本中不同样本之间的相似度分布构成了类内相似度空间; 不同类样本中样本之间的相似度空间形成了类间相似度空间。则每个分块的类内相似度均值和方差可通过如下公式计算得到。类内相似度均值为:

$\begin{matrix} m_{I, b} = \frac{1}{C} \overset{C}{\sum_{i = 1}} \frac{2}{N_{i} (N_{i} - 1)} \overset{N_{i}}{\sum_{k = 2}} \overset{k - 1}{\sum_{j = 1}} χ^{2} (S_{b}^{(i, j)}, M_{b}^{(i, k)}) (9) \end{matrix}$

类内相似度方差为:

$\begin{matrix} S_{I, b}^{2} = \overset{C}{\sum_{i = 1}} \overset{N_{i}}{\sum_{k = 2}} \overset{k - 1}{\sum_{j = 1}} [χ^{2} (S_{b}^{(i, j)}, M_{b}^{(i, k)}) - m_{I, b}]^{2} (10) \end{matrix}$

式中: $\begin{matrix} S_{b}^{(i, j)} \end{matrix}$ 、 $\begin{matrix} M_{b}^{(i, k)} \end{matrix}$ 分别表示第i个分类中的第j个和第k个样本的统计直方图; N_i表示属于第i类的样本数目; b表示当前分块的标识。

同理, 可以得到每个分块的类间相似度均值和方差。类间相似度均值为:

$\begin{matrix} \begin{matrix} m_{E, b} = \frac{2}{C (C - 1)} \overset{C - 1}{\sum_{i = 1}} \overset{C}{\sum_{j = i + 1}} \frac{1}{N_{i} N_{j}} \\ \overset{N_{i}}{\sum_{k = 1}} \overset{N_{j}}{\sum_{l = 1}} χ^{2} (S_{b}^{(i, k)}, M_{b}^{(i, l)}) (11) \end{matrix} \end{matrix}$

类间相似度方差为:

$\begin{matrix} S_{E, b}^{2} = \overset{C - 1}{\sum_{i = 1}} \overset{C}{\sum_{j = i + 1}} \overset{N_{i}}{\sum_{k = 1}} \overset{N_{j}}{\sum_{l = 1}} (χ^{2} (S_{b}^{(i, k)}, M_{b}^{(j, l)}) - m_{E, b})^{2} (12) \end{matrix}$

最终第b个分块的权重可以通过如下公式计算得到:

$\begin{matrix} w_{b} = \frac{(m_{I, b} - m_{E, b})^{2}}{S_{I, b}^{2} + S_{E, b}^{2}} (13) \end{matrix}$

如果某个分块的类内类间相似度均值相差很大而方差又比较小, 那么该分块的统计直方图特征具有更强的识别能力, 一个相应的比较大的权重应该赋值给这个分块; 否则, 该分块的权重则较小。由此, 通过给定样本计算可以得到不同分块的权重。如图5所示, 对Gabor增强纹理图像以8× 8分块处理, 将通过Fisher准则计算得到的权值量化到1和8之间。其中, 暗色区域对应的权值较小, 亮色区域对应的权值较大。

	Figure Option View Download New Window
	图5 通过Fisher准则统计得到的权重分配信息, 权重值为1~8Fig.5 Weight value normalized to 1~8 abtained by Fisher criterion

4 实验及结果分析

目前常用的视频人脸数据库包括Honda/UCSD数据库和Mobo(Motion of body)数据库等。Honda/UCSD数据库包含20个不同人的视频段, 其中训练集视频20段, 测试集视频39段, 提取的视频人脸图像经归一化后为183像素× 229像素。

本文分别观察了VLBP、LBP-TOP、Gabor变换幅值的VLBP(GVLBP)、Gabor变换幅值的LBP-TOP(GLBP-TOP)以及采用了Fisher加权准则的GLBP-TOP(WGLBP-TOP)五种不同算法的识别性能。分类器选择基于Chi平方概率统计的最近邻方法。当视频帧集合大小为7帧时, 五种不同算法的参数选择及分类结果如表1和图6所示。

表1 不同算法在Honda/UCSD视频人脸数据库上的首选识别率 Table 1 Recognition rate of different algorithms

算法	识别率/%
* VLB $\begin{matrix} {P_{2}}_{, 4, 1} \end{matrix}$ +1NN VLB $\begin{matrix} {P_{1}}_{, 4, 1} \end{matrix}$ +1NN	33.3 38.5
GVLBP_{1, 4, 1}+1NN	53.8
* LBP-TOP_{4, 4, 4, 1, 1, 1}+1NN	53.8
LBP-TOP_{8, 8, 8, 1, 1, 1}+1NN	56.4
GLBP-TOP_{8, 8, 8, 1, 1, 1}+1NN	66.7
WGLBP-TOP_{8, 8, 8, 1, 1, 1}+1NN	69.2

表1 不同算法在Honda/UCSD视频人脸数据库上的首选识别率 Table 1 Recognition rate of different algorithms

	Figure Option View Download New Window
	图6 不同算法在Honda/UCSD视频库上的CMC曲线Fig.6 The CMC of different algorithms on Honda/UCSD database

4.1 算法参数选择分析

在VLBP_L_,_P_,_R算子描述中, P的大小直接影响到算子提取的特征直方图维度, P越大, 参与计算的邻域像素个数越多, 局部纹理描述更加细致, 但对应的特征直方图维度较高, 所以P不建议取值过大^[9]。表1中分别给出了(L=2, P=4)和(L=1, P=4)的情形下算法的识别率。

在LBP-TO $\begin{matrix} P_{P_{XY}, P_{XT}, P_{YT}, R_{X}, R_{T}, R_{Y}} \end{matrix}$ 算子描述中, P_XY、P_XT、P_YT分别表示XY平面、XT平面、YT平面的邻域像素个数; R_X、R_T、R_Y分别为三个平面的邻域圆周半径。从表1中可以看出, 邻域像素P值越大, 识别率越高。在某些情况下, 出于降低特征维度的考虑, 选择P=4要更优于选择P=8, 可以使特征维度由768降低至48。所以, 最优P的取值同VLBP算法一样, 取决于实际需要以及数据集的规模。

本文算法通过结合Gabor变换和LBP-TOP算子的独特优势提取出了多角度特征融合的视频人脸纹理特征, 从而有效地增强了特征直方图的表示能力。通过在不同时间段采集的测试视频集合中与其他基准算法进行对比, 验证了该方法的有效性。同时, 该方法对光照变化、表情变化等具有良好的鲁棒性。

4.2 视频帧集合大小测试

在本文算法中, 视频帧集合的大小对识别率的影响较大。对Honda/UCSD数据库训练集和测试集中所有人脸视频进行逐帧统计分析发现, 正面人脸持续的平均时间不超过10帧, 超出10帧的人脸会发生3D旋转, 而当视频帧集合过小(如3帧)时, 识别率已经低于50%。所以本文重点考查了当帧集合大小为5、7和9时, 各算法的识别性能。

从表2和图7中可以看出:随着视频帧集合的增大, 可以一定程度上带来较高的识别率, 但时间复杂度也会随之增加。

表2 视频帧集合大小对识别率及运行时间的影响 Table 2 Recognition rate and time consumed of different size of frames

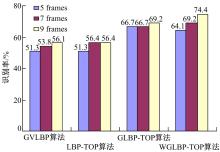	Figure Option View Download New Window
	图7 各算法选取不同大小视频帧集合的首选识别率Fig.7 Recognition rate of different algorithms with different sizes of video frame set

本文基于Honda/UCSD数据库对视频帧集合大小对识别率的影响分析进行了大量实验, 对GVLBP、GLBP-TOP这两种性能较好的算法进行的统计分析的实验结果如图8所示。

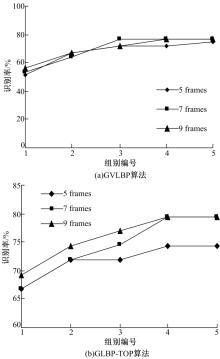	Figure Option View Download New Window
	图8 GVLBP和GLBP-TOP算法在不同大小视频帧集合的CMC曲线Fig.8 The CMC of different sizes of video frame set by GVLBP and GLBP-TOP algorithms

从图8可以看出:随着视频帧集合的增大, 可辨别性信息的增多, 识别性能在一定程度上得到了提高, 但可辨别性信息增多的同时, 视频帧带来的噪音等影响识别率的因素也随之增多, 在不同环境下的实际应用中应兼顾性能和时间复杂度。

4.3 算法复杂度分析

单个视频序列可以认为是以时间轴T为中心的XY面的堆叠, 当各算法在XY、XT和YT平面都考虑P个邻域像素时, VLBP算法的计算复杂度为O(XYT· 2^3P)^[9], LBP-TOP算法的计算复杂度为O(XYT· 2^P)^[9], 本文通过在Gabor人脸幅值图像中提取LBP-TOP算子可以快速、有效地进行视频人脸纹理的表示及识别, 得到更好的识别效果。

5 结束语

由于采用了Gabor小波、LBP-TOP算子的特征直方图等兼顾局部特征变化和全局视频特征分布的多角度特征融合的视频人脸纹理表示及识别方法, 因而对光照、表情变化等问题具有较高的鲁棒性。从视频帧集合的角度考虑进行人脸描述及识别可以有效地利用时空连续性信息, 提高识别精度, 但带来的噪音等影响识别性能的因素也同时增多, 另外, 最近邻分类方法的效率还有待提高。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Barr J R, Bowyer K W, Flynn P J, et al. Face recognition from video: a review[J]. International Journal of Pattern Recognition and Artificial Intelligence, 2012, 26(5): 1266002-1266054. [本文引用:1]
[2]	Jafri R, Arabnia H R. A survey of face recognition techniques[J]. Journal of Information Processing Systems, 2009, 5(2): 41-68. [本文引用:1]
[3]	Belhumer P, Hespanha P, Kriegman D. Eigenfaces vs fisherfaces: recognition using class specific linear projection[J]. IEEE Trans on PAMI, 1997, 19(7): 711-720. [本文引用:1]
[4]	Huang D, Shan C F, Ardabilian M, et al. Local bi-nary patterns and its application to facial image analysis: a survey[J]. IEEE Trans on Systems, Man, and Cybernetics, 2011, 41(6): 765-781. [本文引用:1]
[5]	Zhao G Y, Ahonen T, Matas J, et al. Rotation-invariant image and video discription with local binary pattern features[J]. IEEE Trans on Image Processing, 2012, 21(4): 1465-1477. [本文引用:1]
[6]	Liu C J, Wechsler H. Gabor feature based classification using the enhanced fisher linear discriminant model for face recognition[J]. IEEE Trans on Image Processing, 2002, 11(4): 467-476. [本文引用:1]
[7]	Ojala T, Pietikainen M, Maenpaa T. Multi-resolution gray-scale and rotation invariant texture classification with local binary patterns[J]. IEEE Trans on PAMI, 2002, 24(7): 971-987. [本文引用:1]
[8]	Ahonen T, Hadid A, Pietikainen M. Face description with local binary patterns: application to face recognition[J]. IEEE Trans on PAMI, 2006, 28(12): 2037-2041. [本文引用:1]
[9]	Zhao G, Pietikainen M. Dynamic texture recognition using local binary patterns with an application to facial expressions[J]. IEEE Trans on PAMI, 2007, 29(6): 915-928. [本文引用:4]
[10]	Chan C H, Tahir M A, Kittler J, et al. Multi-scale local phase quantization for robust component-based face recognition using kernel fusion of multiple descriptors[J]. IEEE Trans on PAMI, 2013, 35(5): 1164-1177. [本文引用:1]
[11]	Moghaddam B, Jebara T, Pentland A. Bayesian face recognition[J]. Pattern Recognition, 2000, 33(11): 1771-1782. [本文引用:1]

2012

0.0

... 相对于静态图像,动态视频中可选用的特征信息更加丰富多样^[1],例如,视频的时间动态信息有助于识别率的提升 ...

2009

0.0

... 视频人脸识别方法主要分为两类:一类是设法提取出视频序列中最具代表性的单独人脸帧图像,采用传统的基于静态图像的人脸识别方法^[2,3],包括基于几何特征的方法、基于统计的方法等对人脸进行识别 ...

1997

0.0

2011

0.0

... 另外一类就是将视频看成是一个视频帧集合^[4,5],从帧集合的角度进行分析,利用3D建模、时空连续信息的概率模型、设计视频纹理描述等方法提高识别率,在这类方法中如何充分利用视频中人脸的时间和空间信息克服视频中人脸分辨率低,光照、表情、姿态变化剧烈等困难是研究的重点 ...

2012

0.0

2002

0.0

... 在人脸识别领域中,Gabor变换得到了广泛的应用,如基于Gabor特征的Fisher判别人脸识别^[6]等 ...

2002

0.0

... 2 三个正交平面上的局部二值模式LBP算子于1996年由Ojala等提出^[7,8],是一种从纹理局部近邻定义中衍生出来在灰度范围内的纹理度量算子 ...

2006

0.0

... 2 三个正交平面上的局部二值模式LBP算子于1996年由Ojala等提出^[7,8],是一种从纹理局部近邻定义中衍生出来在灰度范围内的纹理度量算子 ...

2007

0.0

... 为了解决上述问题,提出了LBP-TOP^[9]算子,并在此基础上衍生出多种纹理表示算法^[10] ...

... 1 算法参数选择分析在VLBP_L_,_P_,_R算子描述中,P的大小直接影响到算子提取的特征直方图维度,P越大,参与计算的邻域像素个数越多,局部纹理描述更加细致,但对应的特征直方图维度较高,所以P不建议取值过大^[9] ...

... 2^3P)^[9],LBP-TOP算法的计算复杂度为O(XYT#cod#x000b7 ...

... 2^P)^[9],本文通过在Gabor人脸幅值图像中提取LBP-TOP算子可以快速、有效地进行视频人脸纹理的表示及识别,得到更好的识别效果 ...

2013

0.0

... 为了解决上述问题,提出了LBP-TOP^[9]算子,并在此基础上衍生出多种纹理表示算法^[10] ...

2000

0.0

... Fisher准则^[11]的基本思想是通过使类内散度尽可能小,而类间散度尽可能大来分析每个区域的权值,用于评估不同人脸区域的辨别能力,该准则已经得到广泛的应用 ...