航空瞬变电磁反演中灵敏度的快速高精度计算

引用本文

王琦, 林君, 于生宝, 王凌群, 李冰冰, 朱凯光. 航空瞬变电磁反演中灵敏度的快速高精度计算. 2015, 45(6): 2020-2025
WANG Qi, LIN Jun, YU Sheng-bao, WANG Ling-qun, LI Bing-bing, ZHU Kai-guang. Calculation of sensitivities for airborne electromagnetic inversion progress. Journal of Jilin University Engineering and Technology Edition, 2015, 45(6): 2020-2025 复制到剪切板

Permissions

航空瞬变电磁反演中灵敏度的快速高精度计算

王琦^1,², 林君^1,², 于生宝^1,², 王凌群^1,², 李冰冰^1,², 朱凯光^1,²

1.吉林大学地球信息探测仪器教育部重点实验室,长春 130026

2.吉林大学仪器科学与电气工程学院,长春 130026

朱凯光(1970-),女,教授,博士生导师.研究方向:地球物理电磁探测及随机信号处理.E-mail:zhukaiguang@jlu.edu.cn

作者简介:王琦(1988-),女,博士研究生.研究方向:航空电磁法正、反演.E-mail:wangqi19880115@126.com

基金:国家自然科学基金项目(41274076); “863”国家高技术研究发展计划项目(2013AA063904); 国家重大科研装备研制项目(ZDYZ 2012_1_03); 吉林大学研究生创新基金项目(2014023)

摘要

为了满足在航空电磁反演迭代过程中灵敏度的计算要求,提出了多步长差分累加算法,以差分代替微分计算,用差分步长系数控制累加次数,通过多个步长中心差分结果的累加平均,实现了灵敏度的快速高精度计算。计算了多组大地模型灵敏度,结果表明:差分步长系数选取10,灵敏度矩阵元素的误差均可控制在0.1%以内。与传统中心差分方式和解析法进行对比分析,得到多步长差分累加算法在计算精度上优于中心差分方法;在计算速度上优于解析法,对于15层大地模型,计算速度提高5倍。最后,通过航空瞬变电磁反演仿真实例,证明了该算法能够满足航空电磁海量数据对反演精度和反演速度的要求。

关键词: ; 勘查技术; 航空瞬变电磁; 灵敏度; 多步长差分累加算法; 反演

中图分类号:P631 文献标志码:A 文章编号:1671-5497(2015)06-2020-06

Calculation of sensitivities for airborne electromagnetic inversion progress

WANG Qi^1,², LIN Jun^1,², YU Sheng-bao^1,², WANG Ling-qun^1,², LI Bing-bing^1,², ZHU Kai-guang^1,²

1.Key Laboratory of Geo-Exploration Instrumentation, Ministry of Education,Jilin University, Changchun 130026, China

2.College of Instrumentation & Electrical Engineering, Jilin University, Changchun 130026, China

Abstract

To meet the requirements of the sensitivities during the airborne electromagnetic inversion iteration, a variable step size difference accumulation algorithm is proposed. Based on the idea of replacing the derivative by difference, and adjusting the accumulating time by difference step coefficient, a fast high-precision algorithm is realized. The sensitivity matrix of multi-group earth model is calculated. The results show that the error of the sensitivity matrix is within 0.1% when the coefficient of difference step is usually selected 10. Comparison with the routine center differential algorithm and the analytical method indicates that the variable step size difference accumulation algorithm is superior to center differential algorithm in calculation accuracy, and is better than analytical method in calculation speed. Finally, the proposed algorithm is applied to airborne inversion simulation to prove its effectiveness.

Keyword: perambulation technology; airborne time domain electromagnetic; sensitivities; variable step size difference accumulating algorithm; inversion

Show Figures

0 引言

航空瞬变电磁法(Airborne time-domain ele-ctromagnetic methods, AEM)是一种搭载在飞机平台上的基于电磁感应原理的电磁探测方法。利用发射线圈向地下发送瞬变磁场(一次场), 激发地下良导体感生涡旋电流(二次感应电流), 在电流关断期间, 观测按指数规律衰减的二次场(二次感应电压), 再通过对电磁数据的反演成像获取地下电性信息。灵敏度的计算在反演过程中十分重要, 其计算精度将直接影响反演结果的精度^{[1, 2, 3, 4, 5]}; 同时反演过程需要进行多次迭代, 即多次计算灵敏度, 灵敏度的计算速度影响反演速度, 特别是对于航空电磁探测的海量数据反演, 灵敏度的计算速度尤为重要。

随着计算机技术的发展, 对于灵敏度的计算, 通常有解析法和近似法两种方法。解析法即直接对正演算子求偏导, 可转化为对反射系数求偏导, 该方法计算精度高, 但计算速度较慢。大地模型层数越多, 反射系数越复杂, 计算越耗时, 因此在实际应用中适用于简单大地模型的一维反演, 不适用于多层一维大地模型和二维、三维模型反演。近似法中应用较为广泛的有差分法和拟牛顿更新法。差分即选取适当的差分步长, 对理论电磁感应数值进行差分, 虽然计算步骤简单、速度较快, 但是计算结果精度较低, 仅在一定条件下能满足反演精度的要求^{[6, 7]}; 拟牛顿法在第一次反演迭代中求出灵敏度, 第一次反演迭代之后, 采用拟牛顿法对灵敏度进行更新, 虽然该方法相对于差分法计算精度有所提高, 相对于对正演算子直接求偏导的方法耗时有所减小, 但对于高维反演问题, 仍需要提高计算速度, 节省反演计算时间^{[8, 9, 10, 11]}。因此, 本文提出了一种既能保证计算精度又可提高计算速度的灵敏度计算方法, 特别适用于航空电磁海量数据的反演成像。

本文针对传统航空电磁反演迭代中灵敏度计算精度和计算速度需兼顾的问题, 提出了基于中心差分方法的多步长累加算法, 即将多个步长的中心差分结果相加取平均值, 并将其与传统的中心差分计算方法和解析计算方法的计算精度和计算速度进行了对比分析。最后给出了航空电磁反演仿真结果, 验证了算法的有效性。

1 基本原理

1.1 灵敏度矩阵

航空电磁反演过程即寻找一个大地模型, 并计算其电磁响应, 使响应数据与实测数据拟合误差达到最小。反演的目标函数为:

$\begin{matrix} \begin{matrix} Φ (m) = ‖ d^{obs} - F (m) ‖^{2} = \\ [d^{obs} - F {(m)]}^{T} C_{d}^{- 1} [d^{obs} - F (m)] (1) \end{matrix} \end{matrix}$

式中:d^obs为实测数据; F(m)为正演函数, 模型参数m的物理意义为大地模型的电导率σ _k和厚度d_k; $\begin{matrix} C_{d}^{- 1} \end{matrix}$ 为数据加权矩阵。

令式(1)对大地模型参数的导数为零, 则得到目标函数最小值:

$\begin{matrix} \begin{matrix} \frac{\partial}{\partial m} [d^{obs} - F {(m)]}^{T} C_{d}^{- 1} [d^{obs} - F (m)] = 0 \\ (2) \end{matrix} \end{matrix}$

利用泰勒级数展开将F(m)线性化, 舍弃高次项, F(mⁿ)≅F(m^n-¹)+J_n· (m-m^n-¹), m^n-¹为上一次反演迭代得到的模型向量; J_n为灵敏度矩阵, 其元素对各模型参数的一阶偏导^{[12, 13]}为:

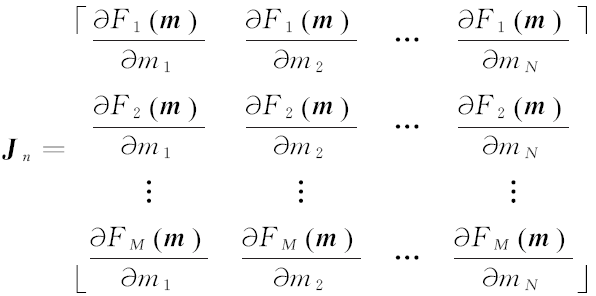
式中:M为反演中数据个数; N为模型参数的个数。

对于灵敏度矩阵元素的计算, 传统的中心差分方法只采用一个差分步长, 利用两组响应数据计算灵敏度, 如式(3)所示:

$\begin{matrix} \begin{matrix} \frac{\partial F_{i} (m)}{\partial m_{j}} = \frac{F_{i} (m_{j} - Δ) - F_{i} (m_{j} + Δ)}{2 Δ} \\ (3) \end{matrix} \end{matrix}$

式中:F_i $\begin{matrix} (m_{j} - Δ) \end{matrix}$ 、F_i $\begin{matrix} (m_{j} + Δ) \end{matrix}$ 分别为两组模型参数的电磁响应理论值; Δ 为差分步长, 当步长较大时, 导致差分结果误差增大; 当步长较小时, 使差分结果产生震荡, 差分步长的选择对结果影响较大。

1.2 多步长差分累加算法

针对传统中心差分灵敏度计算方法的不足, 本文提出了一种多步长中心差分累加的计算方法。以固定翼航空电磁z分量电磁响应反演为例, 对该算法进行详细说明。

(1)选定模型参数m的初始差分步长Δ , 利用正演公式(4), 分别计算模型参数为[m₁, …, m_j-Δ , …, m_N]和[m₁, …, m_j+Δ , …, m_N]的电磁响应理论值F $\begin{matrix} (m'_{j -}) \end{matrix}$ 、F $\begin{matrix} (m'_{j +}) \end{matrix}$ :

$\begin{matrix} \begin{matrix} F (m) = \int_{0}^{\infty} R_{0} (m, λ) λ^{2} e^{- λ (z_{0} + h_{0})} J_{0} (λr) dλ \\ (4) \end{matrix} \end{matrix}$

式中:h₀为发射线圈高度; z₀为接收线圈高度; r为系统的水平收发距; J₀为零阶贝塞尔函数; λ 为积分变量; R₀为反射系数, R₀=(N₀-Y₁)/(N₀+Y₁), N₀=λ /(iμ ₀ω ), Y₁通过递推公式:Y_k=N_k $\begin{matrix} \frac{Y_{k + 1} + N_{k} \tanh (u_{k} d_{k})}{N_{k} + Y_{k + 1} \tanh (u_{k} d_{k})} \end{matrix}$ 计算, k=n-1, n-2, …, 1, Y_n=N_n, N_k= $\begin{matrix} \frac{u_{k}}{i μ_{k} ω} \end{matrix}$ , u_k= $\begin{matrix} \sqrt{λ^{2} + i μ_{k} σ_{k} ω} \end{matrix}$ , 空气磁导率μ ₀=4π × 10^-7 H/m。

计算F $\begin{matrix} (m'_{j -}) \end{matrix}$ 、F $\begin{matrix} (m'_{j +}) \end{matrix}$ 两组理论响应值的中心差分结果。

(2)取多个差分步长, 并利用步骤(1)计算其中心差分。最后将多组不同差分步长相累加并取平均值, 即得到高精度的灵敏度矩阵元素。实现方法如式(5)所示:

$\begin{matrix} \begin{matrix} J_{ij} = \overset{K}{\sum_{α = 1}} \frac{F_{i} (m_{j} + αΔ) - F_{i} (m_{j} - αΔ)}{K \cdot 2 Δ} \\ (5) \end{matrix} \end{matrix}$

式中:α 为差分步长系数, α =1, 2, …, K。

当α 等于1时, 式(5)为差分步长是Δ 的传统中心差分; 当α 大于1时, 式(5)即为将多个差分步长逐渐增大(α 越大差分步长越大)的中心差分结果相加取平均。该方法可根据不同的大地模型和精度要求, 选取不同的α 。通常对计算精度要求越高, α 取值越大, 但计算速度也会随之降低。

2 计算实例及分析

2.1 计算实例

为验证本文算法的可行性, 利用MATLAB进行数值仿真实验。以15层大地模型为例, 每层厚度为20 m, 利用式(3)计算多个电导率大地模型的灵敏度, 其中Δ 取值为0.000 002, α 在1~40区间变化, 采样时刻为在0.01 ms~10 ms间等对数间隔的14个点。本文选取两个模型进行说明。

当大地模型各层电导率均为1 S/m时, 第2层大地的灵敏度矩阵部分元素的相对误差(以解析法的结果为真值)如图1所示。当大地模型各层电导率均为0.01 S/m时, 第10层大地的部分采样时刻的灵敏度相对误差如图2所示。通过图1和图2可以得出, 灵敏度矩阵元素的误差随α 值的增大而减小, 且α 取值为1~3时, 误差减小速度很快; α 取值为4~30时, 误差减小速度相对平缓; α 在30~40区间, 误差减小速度十分缓慢。

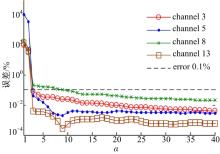	Figure Option View Download New Window
	图1 电导率为1 S/m时, 第2层大地模型灵敏度相对误差随多步长差分累加算法中α 值的变化规律Fig.1 Sensitivities relative error of the second-layer with α , when the conductivity is 1 S/m

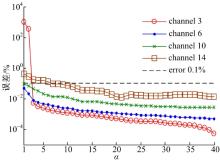	Figure Option View Download New Window
	图2 电导率为0.01 S/m时, 第10层大地模型灵敏度相对误差随多步长差分累加算法中α 值的变化规律Fig.2 Sensitivities relative error of the tenth-layer with α , when the conductivity is 0.01 S/m

当α 等于3时, 灵敏度矩阵中各元素相对误差均在1%以下; 当α 等于10时, 灵敏度矩阵中各元素的相对误差均已达到0.1%以下。因此在航空电磁反演中, 通常取α 等于10, 即可满足反演精度的要求。

2.2 计算精度对比分析

为进一步说明算法的优越性, 将其计算精度与传统中心差分方法的计算精度进行比较。采用2.1节中的仿真条件, 选取差分步长在模型的1%左右(根据中心差分方法中差分步长选取经验), 采用中心差分方法计算多组不同差分步长的灵敏度矩阵中部分元素的相对误差, 结果如图3和图4所示。由图3和图4可以得出, 灵敏度元素的误差随差分步长的变化无明显规律。利用中心差分的计算方法, 虽然部分晚期采样时刻的灵敏度误差较小, 但部分早期采样的灵敏度误差高达100%以上, 在反演迭代中不可用, 并且仅改变差分步长并不能明显提高灵敏度精度。

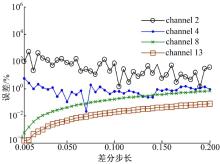	Figure Option View Download New Window
	图3 电导率为1 S/m时, 第2层大地模型灵敏度相对误差随中心差分方法中差分步长的变化规律Fig.3 Sensitivities relative error of the second-layer with differencestep, when the conductivity is 1 S/m

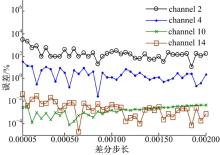	Figure Option View Download New Window
	图4 电导率为0.01 S/m时, 第10层大地模型灵敏度相对误差随中心差分方法中差分步长的变化规律Fig.4 Sensitivities relative error of the tenth-layer with difference step, when the conductivity is 0.01 S/m

通过对比图1和图2、图3和图4可以得出, 本文提出的快速高精度的多步长中心差分累加灵敏度计算方法与中心差分方式相比, 大大减小了计算结果的误差。

2.3 计算速度对比分析

在保证计算精度的前提下(α 取10), 将多步长中心差分累加算法的计算速度与传统解析法的计算速度进行对比。分别计算了两种方法计算5层、10层、15层大地模型灵敏度所需的时间, 结果如表1所示。由表1可以得出, 对于简单的5层大地模型, 多步长中心差分累加算法与解析法计算速度基本相同。但是对于10层和15层大地模型, 多步长中心差分累加算法的计算速度仅为解析法的1/4和1/5。说明本文提出的多步长中心差分累加算法尤其适用于实际应用中较为复杂的多层大地模型。

表1 计算不同大地模型灵敏度所需时间(s) Table 1 Time needed for calculating sensitivities of different earth model(s)

3 应用实例

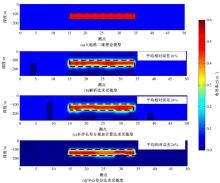
为了验证多步长累加算法在航空电磁反演中的实用性, 本文采用50个大地模型相互连接, 设计了含有高导异常的准二维模型, 如图5(a)所示。在测点15~35处有一个厚度为60 m的异常体, 埋藏深度为100 m, 异常体电导率为0.5 S/m, 周围基岩电导率为0.05 S/m。利用式(4)对上述大地模型进行正演计算, 获得电磁响应数据, 并加入5%的高斯噪声。

	Figure Option View Download New Window
	图5 反演结果对比图Fig.5 Pseudo-2D model inversions diagram with Occam's

采用二阶粗糙度因子的Occam方法^{[14, 15]}对仿真航空电磁数据进行反演, 模型层数为15层, 初始模型采用电导率为0.1 S/m的均匀半空间。反演迭代中, 敏感度矩阵分别采用精度较高的解析法、多步长中心差分累加算法和中心差分算法进行计算, 反演结果如图5(b)(c)(d)所示。对比图5(a)(b)(c)(d)可以看出, 两种精度较高的敏感度计算方法的反演结果均能清晰地显示地下导电薄层的埋深及厚度信息, 与理论模型一致, 而图5(d)中对23点~28点反演结果异常体电导率小于模型电导率值, 而围岩电导率大于模型电导率值。反演迭代中利用多步长差分累加计算方法求取灵敏度, 反演结果的平均相对误差比差分法提高了8%。因此, 采用本文提出的多步长差分累加计算方法进行反演迭代中灵敏度的计算不仅提高了反演速度, 同时也保证了反演精度。

4 结束语

针对航空电磁反演中传统灵敏度计算方法的不足, 提出了快速高精度的多步长中心差分累加的计算方法。差分步长系数选取10, 大地模型灵敏度矩阵元素的误差在0.1%内; 且对于同一15层大地模型, 本方法计算耗时仅为利用解析方法计算的1/5。准二维反演仿真实例中, 利用多步长差分累加计算方法计算灵敏度, 反演结果的平均相对误差较差分法降低了8%, 进一步证明了算法的实用性。在实际应用中, 该方法同样适用于地面瞬变电磁反演中灵敏度的计算。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	晋光文. 大地电磁资料的灵敏度研究[J]. 地球物理学报, 1991, 34(3): 465-473. Jin Guang-wen. Research on sensitivities for the magnetotelluric data[J]. Chinese Journal of Geophysics, 1991, 34(3): 465-473. [本文引用:1]
[2]	肖晓, 汤井田. 大地电磁测深二维灵敏度分析[C]∥第十届中国国际地球电磁学术讨论会论文集. 南昌, 2011: 230-232. Xiao Xiao, Tang Jing-tian. Sensitivity analysis of two-dimensional magnetotelluric data[C]∥The 10th China International Geo-electromagnetic Workshop. Nanchang, 2011: 230-232. [本文引用:1]
[3]	Farquharson C G, Oldenburg D W. Approximate sensitivities for the electromagnetic inverse problem[J]. Geophysical Journal International, 1996, 126(1): 235-252. [本文引用:1]
[4]	McGillivray P R, Oldenburg D W. Calculation of sensitivities for the frequency-domain electromagnetic problem[J]. Geophysical Journal International, 1994, 116(1): 1-4. [本文引用:1]
[5]	沈金松, 孙文博. 电磁响应的互换原理及其在响应灵敏度计算中的应用[J]. 勘探地球物理进展, 2008, 31(1): 25-33. Shen Jin-song, Sun Wen-bo. Reciprocity of electromagnetic response and its application in sensitivity calculation[J]. Progress in Exploration Geophysics, 2008, 31(1): 25-33. [本文引用:1]
[6]	李建平, 李桐林, 张辉, 等. 不规则回线源层状介质瞬变电磁场正反演研究及应用[J]. 吉林大学学报: 地球科学版, 2006, 35(6): 790-795. Li Jian- ping, Li Tong-lin, Zhang Hui, et al. Study and application of the TEM forward and inversion problem of irregular loop source over the layered medium[J]. Journal of Jilin University (Earth Science Edition), 2006, 35(6): 790-795. [本文引用:1]
[7]	林长佑, 扬世荣. 瞬变电磁晚期场资料的一维反演[J]. 西北地震学报, 1994, 16(2): 71-78. Lin Chang-you, Yang Shi-rong. 1D inversion of transient electromagnetic late time field[J]. Northwestern Seismological Journal, 1994, 16(2): 71-78. [本文引用:1]
[8]	熊彬, 罗延钟, 强建科. 瞬变电磁2. 5维反演中灵敏度矩阵计算方法[J]. 地球物理学进展, 2004, 19(3): 616-620. Xiong Bin, Luo Yan-zhong, Qiang Jian-ke. Methods for calculating sensitivities for 2. 5-D transient electromagnetic inversion[J]. Progress in Geophysics, 2004, 19(3): 616-620. [本文引用:1]
[9]	毛立峰. 超宽带电磁法正演模拟及反演成像[D]. 成都: 成都理工大学信息工程学院, 2007. Mao Li-feng. The forward simulation and inversion imaging of the ultra wide band electromagnetic method[D]. Chengdu: College of Information Engineering, Chengdu University of Technology, 2007. [本文引用:1]
[10]	胡祖志, 胡祥云, 何展翔. 大地电磁非线性共轭梯度拟三维反演[J]. 地球物理学报, 2006, 49(4): 1226-1234. Hu Zu-zhi, Hu Xiang-yun, He Zhan-xiang. Pseudo-three-dimensional magnetotelluric inversion using nonlinear conjugate gradients[J]. Chinese Journal of Geophysics, 2006, 49(4): 1226-1234. [本文引用:1]
[11]	Rodi W, Mackie R L. Nonlinear conjugate gradients algorithm for 2-D magnetotelluric inversion[J]. Geophysics, 2001, 66(1): 174-187. [本文引用:1]
[12]	Spitzer K. The three-dimensional dc sensitivity for surface and subsurface sources[J]. Geophysical Journal International, 1998, 134(3): 736-746. [本文引用:1]
[13]	罗勇. 时间域航空电磁一维正反演研究[D]. 成都: 成都理工大学地球物理学院, 2013. Luo Yong. The modeling and inverse of one dimensional time domain electromagnetic[D]. Chengdu: College of Geophysics, Chengdu University of Technology, 2013. [本文引用:1]
[14]	Constable S C, Parker R L, Constable C G. Occam's inversion; a practical algorithm for generating smooth models from electromagnetic sounding data[J]. Geophysics, 1987, 52(3): 289-300. [本文引用:1]
[15]	周道卿, 谭捍东, 王卫平. 频域航空电磁资料Occam反演研究[J]. 物探与化探, 2006, 30(2): 162-165. Zhou Dao-qing, Tan Han-dong, Wang Wei-ping. The Occam inversion in FAEM data processing[J]. Geophysical & Geochemical Exploration, 2006, 30(2): 162-165. [本文引用:1]

1991

0.0