作者简介:高明亮(1987-),男,博士研究生.研究方向:高密度电法勘探非线性反演.E-mail:mlgao13@mails.jlu.edu.cn
针对神经网络算法在非线性反演中容易陷入局部极小、收敛慢、反演精度差等问题,提出了将粒子群优化(Particle swarm optimization)算法与BP神经网络(Back propagation neural networks)进行混合反演(简称PSBP)。最后,通过经典的地电模型对本文方法的有效性进行验证,结果表明,本文方法与线性反演方法、BP神经网络反演方法对比,具有明显的优势,并取得了很好的反演结果。
In nonlinear inversion, neural network algorithm has the shortcomings of easy to fall into local minimum, slow convergence and poor inversion accuracy. To overcome these shortcomings, the Particle Swarm Optimization (PSO) is combined with Back Propagation (BP) neural network to achieve inversion (referred as PSBP). The effectiveness of the PSBP is verified by the classical geoelectric model. Compared with the linear inversion and BP neural network inversion methods, the proposed PSBP method has obvious advantages with good inversion result.
高密度电法是一种阵列式勘探方法, 在野外实验时, 只需将全部电极置于测点上, 通过电极转换开关即可实现数据的快速采集。在后期的数据处理过程中, 大多采用阻尼最小二乘法进行反演。目前广泛应用的二维反演软件是由Loke编写的RES2DINV软件[1, 2]。地球物理中的反演问题, 即由观测数据反推模型参数, 这个过程是一个非线性问题。线性反演方法将非线性问题线性化, 必将存在反演依赖初始模型、反演精度差等问题[3, 4, 5]。BP神经网络(Back propagation neural networks)以其独特的记忆学习能力和非线性逼近能力逐渐得到广泛应用[6, 7, 8]。文献[9-11]率先将神经网络算法引入电阻率测深的一维反演工作中。在2D、3D电阻率非线性反演中, 徐海浪等[1, 12]利用神经网络算法进行了电阻率反演研究, 取得了较好的反演效果。但是单独使用BP神经网络在训练权值和阈值时, 大多采用的是梯度下降法[13, 14, 15], 这就容易造成在权值和阈值的训练过程中存在局部极小、收敛速度慢、反演训练时间长等问题[16, 17, 18]。
针对这个问题, 本文提出将粒子群优化(Particle swarm optimazation)算法与BP神经网络进行混合反演, 即用粒子群算法来优化神经网络的训练过程, 并将其应用于地下电阻率研究, 取得了很好的反演效果。
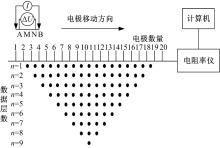
高密度电阻率法是基于常规直流电阻率法原理, 将多种电极排列的常规方法和信息自动处理相结合的勘探方法。通过两个供电电极(A、B)向地下供电, 注入稳恒电流I, 同时在测量电极(M、N)间观测电位差Δ U, 计算出视电阻率ρ S:
式中:K为装置系数, 为已知量。
各电极沿着选定的测线向前移动和观测, 如图1所示。测完整条测线的视电阻率ρ S后, 通过计算机利用最优化算法(例如最小二乘法等), 对物探异常给出定量解释, 形成反演剖面。电阻率法主要是用来探查地下一定深度范围内的横向和纵向电性变化, 以此来解决多种地质问题。
基于BP回传理论的反演方法主要分为学习和反演两个过程, 其中在学习过程中又分为正传和反传两个步骤。由输入和初始化后的连接权计算实际输出, 即正传。反传是由期望输出与实际输出的偏差, 逐层向输入层方向逆向修正, 将偏差分摊给各层单元, 以此调整各个连接权值, 依次迭代, 直到实际输出和期望输出的偏差达到所要求的精度为止[19, 20]。
设ck为第k个输入样本的期望输出; yk为实际输出, 则BP神经网络的目标函数E可以设为所有输入样本的实际输出与期望输出的误差平方和, 如式(2)所示:
式中:q为样本的总个数。
BP神经网络训练方法多为梯度下降法, 即:
式中:wij为网络连接权值; Δ wij(t)为权值的变化量; ε 为学习动量; σ 为学习率, 不断地迭代调整各层间的权值直到E足够小, 网络训练结束。
利用BP神经网络实现反演的步骤如下:
(1)确定输入层和输出层中神经元的个数、隐层的层数及神经元个数(即节点数);
(2)随机初始化权值和阈值, 设定最大迭代次数;
(3)输入学习样本, 根据实际输出和期望输出的误差来调整权值和阈值, 使得期望输出和实际输出的误差达到最小;
(4)样本测试, 测试网络是否训练好;
(5)将训练合格的神经网络来进行电阻率二维反演。
粒子群算法是一种模仿鸟类觅食行为的随机优化算法, 由Kennedy和Eberhart在1995年提出[21]。该算法就是将每个可行解看作是搜索空间的一只鸟, 即粒子, 将多个可行解的集合看作一个种群。该粒子具有的特征是速度和位置。通过设置一个适应度函数来评价粒子的好坏。各个粒子在飞行过程中所到过的最优位置称为个体极值; 整个种群找到的最优解称为全局极值。粒子群算法就是通过在每次迭代过程中根据个体极值和全局极值不断更新自己以寻找最优解的方法。基于原理简单、参数少等优点, 粒子群算法得到了广泛应用。Eberhart和Kennedy用离散二进制粒子群算法来有效地求解工程中的组合优化问题[22, 23]。Clerc[24]用离散二进制粒子群算法对17个城市问题进行测试比较, 研究表明该算法可解决旅行推销员问题(TSP)等组合优化问题。张大莲等[25]将粒子群算法应用在磁测资料井地联合反演中, 取得了比较好的效果, 并且验证了粒子群算法在地球物理反演中的可行性。刘顺安、周立军等[26, 27]将粒子群算法分别应用在汽车悬架优化中和车辆跟驰模型中, 取得了很好的效果, 验证了粒子群算法广泛的适用性。
本文高密度测量电极为45个(极距为2 m)并选择经典的双阻异常体模型用于创建训练神经网络数据集, 其中建立训练数据样本集120个, 测试集5个, 测试集数据均未参与网络训练。
综合考虑反演计算的精度和时间两因素, 并参考相关文献资料, 本文选择有两个隐含层的四层网络进行训练。比较附加动量法、共轭梯度法和RPROP算法(弹性BP算法)发现, 在相同条件下附加动量法训练收敛非常慢, 共轭梯度法训练效果较好, 而RPROP算法最好, 收敛快且精度高, 因此本文选择RPROP训练算法进行电阻率二维神经网络反演[12]。本文把X、Z位置和视电阻率作为神经网络的输入, 以真实电阻率作为神经网络的输出, 这样的数据类型最适合神经网络的训练和测试。
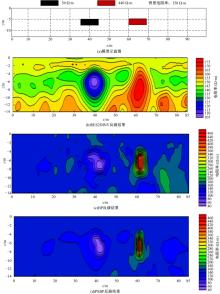
本文选择的算例模型为经典的双电阻模型1, 该模型中背景场的电阻率为150 Ω · m, 其中的两处异常分别为低阻50 Ω · m和高阻440 Ω · m, 地下埋深为5 m, 异常体的尺寸大小为3 m× 3 m, 如图2(a)所示。在神经网络反演中, 选择X、Z位置和视电阻率作为输入; 真实电阻率作为输出。经测试和验证分析, 本文选择双隐含层, 其中第1层神经元数量为40; 第2层神经元数量为30。测试方法如下:分别选择单隐含层、双隐含层和三隐含层的3种神经网络进行对比测试。其中单隐含层节点数目为40个, 双隐含层节点为40、30个, 三隐含层节点数目为40、30、25。图3为三种神经网络的训练误差, 即均方误差随迭代次数的变化。
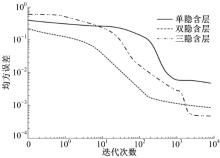 | 图3 不同隐含层的神经网络训练误差随迭代次数的变化Fig.3 Variation of the training error along with the iteration number of the neural network with different hidden layers |
从图3中不难发现, 单隐含层收敛速度慢、误差精度差; 双隐含层和三隐含层收敛速度快, 其中三隐含层误差精度最高。在综合考虑收敛速度和误差精度后, 可知双隐含层神经网络结构最优。故本文选择双隐含层神经网络进行学习训练, 得到最佳的神经预测网络, 然后进行反演预测。最后将神经网络的输出, 即真实电阻率数据应用到SURFER软件上成图, 结果如图2(c)所示。同时应用RES2DINV反演软件也进行了相应成图, 反演结果如图2(b)所示。通过对比不难发现, 利用BP神经网络进行反演虽然产生了冗余构造, 但是在异常体位置和电阻率值上的反演效果比RES2DINV反演更为准确。
针对BP算法在阈值和权值优化过程中容易陷入局部极小的不足, 本文提出PSBP神经网络训练方法, 用粒子群优化算法代替梯度下降法训练神经网络的阈值和权值, 由于粒子群算法可以做到全局寻优, 所以最终迭代出的适应度函数值最小的粒子即为BP神经网络的最佳权值和阈值。PSBP算法步骤如下:
(1)首先根据研究对象建立神经网络结构, 确定输入变量、输出变量; 初始化神经网络输入层、隐含层、输出层的神经元个数。
(2)将神经网络不同层间神经元连接的权值和阈值编码成实数向量, 表示种群中一个粒子。
(3)初始化粒子的初始速度、位置、惯性权值和学习因子, 最大迭代次数。
(4)把神经网络均方误差作为适应度函数, 计算出每个粒子的适应度函数值; 确定每个粒子的个体极值和粒子群的全局极值。
(5)如果粒子当前的位置达到误差要求或者是达到最大迭代次数, 则停止迭代, 此时粒子群的全局极值所对应的权值和阈值即为神经网络的最优权值和阈值。
(6)把最优的权阈值再赋予神经网络, 进行神经网络再训练, 直到达到目标要求或达到最大迭代次数, 输出反演结果。
同样以3.1节的双阻异常体模型为例。首先利用粒子群算法为BP神经网络的初始权阈值进行寻优, 经过45次的迭代寻找到最佳极值点。然后利用单隐含层的BP神经网络进行训练, 经过260次的迭代, 得到最佳的神经网络。最后将PSBP神经网络的输出数据应用SURFER成图处理, 得到反演图, 如图2(d)所示。与图2(b)(c)对比, 显然PSBP得到的反演效果最好。
从图2可以看出, PSBP算法的反演准确度高、效果好。表1为使用RES2DINV线性反演法、BP法和PSBP法进行反演的结果对比表。由表1可以得到以下结论:
| 表1 三种反演算法试验结果对比 Table 1 Comparison of three inversion algorithm test results |
(1)针对神经网络容易陷入局部小、收敛性相对较差的问题, 应用PSO算法对神经网络进行权重优化, PSBP神经网络算法优于BP神经网络, 迭代次数要明显小于BP神经网络, 大大地节约了运算时间。
(2)用BP神经网络法进行反演时需要用双隐层才可以获得较好的网络进行预测, 需要多次调整隐层节点数, 因此迭代次数较多、用时较长, 而PSBP法反演时, 由于先优化了BP神经网络初始权值、阈值, 所以在训练时仅单隐层网络就可得到更优的结果, 时间也相对快些。
(3)预测误差是表明数据稳定性的参数。从3种神经网络方法的预测误差值来看, PSBP要优于BP和RES2DINV线性反演, 在图2(a)所示模型中预测最大绝对值误差, 前者仅为15.3, 后两者高达56.56和82.90。
为了进一步验证PSBP算法的优越性, 本文进行了室内水槽实验验证, 采用温纳-斯伦贝格装置进行测量, 电极极距为1 m, 共使用37个电极。水槽内水电阻率为500 Ω · m, 其中两处异常体均为50 Ω · m的铝塑板, 地下埋深分别为1 m和3 m, 异常体的大小分别为1 m× 3 m和1 m× 5 m, 厚度均为50 cm, 如图4(a)所示。实验共采集210个数据点, 视电阻率断面图如图4(b)所示。
采用3种算法分别对采集的视电阻率进行反演成像, 反演结果如图5所示。由反演结果可知, 从异常体形态上来看, PSBP算法和BP算法均较正确地反映了异常体的位置和电阻率值, 而在轮廓上PSBP算法反演结果更为清晰。而线性反演方法反演结果与实际结果相比失真很大, 无法区分出两个异常体的位置, 并且异常体的阻值也与实际值相差很大。实验结果表明PSBP算法具有较强的泛化能力和鲁棒性。
结合粒子群算法和BP神经网络算法实现了非线性混合反演, 克服了单独使用BP神经网络易陷入局部极小、依赖初始权值选择、反演时间长、收敛速度慢的缺点。通过经典双阻异常模型对算法有效性进行验证, 结果表明, 与BP神经网络反演和线性反演对比, 该算法具有很好的应用前景。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|