基于频域正则维纳滤波的地震随机噪声压制

引用本文

田雅男, 李月, 林红波, 徐学纯. 基于频域正则维纳滤波的地震随机噪声压制. 2015, 45(6): 2043-2048
TIAN Ya-nan, LI Yue, LIN Hong-bo, XU Xue-chun. Frequency-domain regularized Wiener filtering for seismic random noise suppression. Journal of Jilin University Engineering and Technology Edition, 2015, 45(6): 2043-2048 复制到剪切板

Permissions

基于频域正则维纳滤波的地震随机噪声压制

田雅男^1,², 李月¹, 林红波¹, 徐学纯²

1.吉林大学通信工程学院,长春 130012

2.吉林大学地球科学学院,长春 130061

李月(1958-),女,教授,博士生导师.研究方向:地震信号处理,弱信号检测.E-mail:liyue84@gmail.com

作者简介:田雅男(1984-),女,讲师,在站博士后.研究方向:地震信号处理,弱信号检测.E-mail:5999happy@163.com

基金:国家自然科学基金重点项目(41130421); 国家自然科学青年基金项目(41404081)

摘要

在原始目标函数基础上,通过构建附加噪声约束项和正则因子的约束函数的方式,提出了一种频域正则维纳滤波,同时引入信号幅度调节因子,在控制噪声压制强度的同时调节由滤波造成的有效信号损失幅度。此外,利用初至前噪声和含噪记录共同实现随机噪声的谱估计。仿真记录和实际数据的试验结果表明,新算法的滤波效果比中值滤波和传统维纳滤波效果好,信号偏差及有效信号衰减少,验证了新方法正则化思想的可行性和有效性。

关键词: 信号处理; 正则维纳; 地震随机噪声; 噪声约束项; 正则因子

中图分类号:TN911.7 文献标志码:A 文章编号:1671-5497(2015)06-2043-06

Frequency-domain regularized Wiener filtering for seismic random noise suppression

TIAN Ya-nan^1,², LI Yue¹, LIN Hong-bo¹, XU Xue-chun²

1.College of Communication and Engineering, Jilin University, Changchun 130012, China

2.College of Earth Sciences, Jilin University, Changchun 130061, China

Abstract

A Frequency-domain Regularized Wiener Filtering (FDRWF) is proposed. A novel objective function is constructed with an additional noise constrain item and a regularized factor. An amplitude adapting factor is brought in to solve the signal losses resulted from filtering. Moreover, the noise spectrum is estimated by the first arrival noise and noisy record. Experimental results on both synthetic records and field data show that the novel method has superior performance to median filtering and traditional Wiener filtering. Meanwhile, signal losses and derivation are reduced obviously. The effectiveness of the regularized idea in the novel method is proved.

Keyword: signal processing; regularized wiener; seismic random noise; noise constraint item; regularized factor

Show Figures

0 引言

叠前地震资料中的随机噪声压制是地震资料处理的关键环节之一。随着地震勘探技术的发展和地表条件的日益复杂, 地震资料中随机噪声的复杂度和强度不可避免地增强。如何提高地震资料的信噪比一直是人们关注的问题^{[1, 2]}。

已经有许多压制随机噪声的成熟方法, 如中值滤波^[3]、多项式拟合^[4]、小波变换^{[5, 6]}, 时频峰值滤波^[7]和维纳滤波^{[8, 9]}等。这些方法在一定程度上都能够很好地压制随机噪声, 但是又分别存在各自的缺点。维纳滤波器是以最小均方差为约束准则的最佳匹配滤波器, 在地震勘探领域中可应用于含噪地震记录的解卷积^[10]。一方面, 传统的维纳滤波需要已知信号或噪声统计特性的先验知识, 而实际应用中的理想噪声或有效信号很难获得。由于噪声压制效果受到信号或噪声统计特性估计效果的直接影响, 通常只能得到次优的滤波效果。另一方面, 在强噪声低信噪比条件下, 传统维纳滤波的适应性变差, 有效信号幅度衰减严重, 求解滤波因子的方程组的系数矩阵可能出现“ 病态” 现象。

针对地震勘探资料的处理要求及传统维纳滤波存在的这些问题, 本文从均方误差函数出发, 提出了一种频域正则化维纳滤波方法。该方法在原始目标函数基础上附加了带有正则化因子的噪声约束项, 实现对噪声的进一步压制; 为平衡滤波造成的信号失真和噪声压制程度之间的关系, 通过公式推导及效果分析引入信号幅度调节因子; 在仅有含噪观测信号且噪声和信号统计特性未知的条件下, 利用初至前噪声和含噪信号的功率谱实现对噪声功率谱的有效估计。

1 传统维纳滤波

假设噪声为加性噪声且信号和噪声不相关, 维纳滤波的输入信号可以表示为:

$\begin{matrix} x (n) = d (n) + v (n) (1) \end{matrix}$

式中:x $\begin{matrix} (n) \end{matrix}$ 为含噪信号; d $\begin{matrix} (n) \end{matrix}$ 为有效信号; v $\begin{matrix} (n) \end{matrix}$ 为加性噪声。

假设滤波系数为w $\begin{matrix} (n) \end{matrix}$ , 滤波器的输出(也就是期望信号的时域估计)可以表示为:

$\begin{matrix} \hat{d} (n) = w (n) \times x (n) (2) \end{matrix}$

对d $\begin{matrix} (n) \end{matrix}$ 和 $\begin{matrix} \hat{d} \end{matrix} \begin{matrix} (n) \end{matrix}$ 建立最小均方误差准则:

$\begin{matrix} minξ = \min {E [{(d (n) - w (n) \times x (n))}^{2}]} (3) \end{matrix}$

式中:E[· ]表示数学期望; ξ 为均方误差。

当式(3)对w $\begin{matrix} (n) \end{matrix}$ 的偏导数为零时得到w $\begin{matrix} (n) \end{matrix}$ 的求解方程:

$\begin{matrix} R_{xd} (n) = w (n) \times R_{xx} (n) (4) \end{matrix}$

令R_xd为x $\begin{matrix} (n) \end{matrix}$ 与d $\begin{matrix} (n) \end{matrix}$ 的互相关函数R_xd $\begin{matrix} (n) \end{matrix}$ 对应的矩阵; R_xx为x $\begin{matrix} (n) \end{matrix}$ 自相关函数R_xx $\begin{matrix} (n) \end{matrix}$ 对应的矩阵。由于矩阵R_xx的逆阵可能不存在或维数过高, 使得在w $\begin{matrix} (n) \end{matrix}$ 的求解过程中可能会出现“ 病态” 现象, 导致滤波系数求解错误, 严重影响维纳滤波的去噪效果。

2 频域正则维纳滤波

传统维纳滤波在强噪声、低信噪比背景下的地震勘探随机噪声压制过程中存在以下缺陷:①适应性变差; ②由于信号和噪声的频谱存在重叠, 滤除噪声的同时, 有效信号成分受到损失或子波波形畸变; ③由于矩阵的逆阵不存在或输入数据维数过高造成滤波系数求解过程中可能出现“ 病态” 现象。因此本文设计一种频域正则维纳滤波。

所谓正则化方法是指在求解过程中, 用原始数据和噪声的先验知识对解加以约束, 从而获得最佳解^{[11, 12, 13, 14]}。首先, 在传统维纳滤波均方差函数式(3)基础上引入噪声约束项及其正则化因子, 得到新的目标函数:

$\begin{matrix} \begin{matrix} ξ_{r} (n) = Ε {[d (n) - w_{r} {(n) \times x (n)]}^{2}} + \\ αΕ {[w_{r} {(n) \times v (n)]}^{2}} (5) \end{matrix} \end{matrix}$

式中:ξ _r $\begin{matrix} (n) \end{matrix}$ 、w_r $\begin{matrix} (n) \end{matrix}$ 分别为改进后的均方误差函数及维纳滤波系数; α 为正则化因子。

式(5)中第一项为原始均方误差函数项, 第二项为附加的噪声约束项。令式(5)对w_r $\begin{matrix} (n) \end{matrix}$ 的偏导数等于零以保证均方误差函数达到最小值, 从而构建滤波系数求解方程:

$\begin{matrix} - R_{xd} (n) + w_{r} (n) R_{xx} (n) + α w_{r} (n) R_{vv} (n) = 0 (6) \end{matrix}$

根据维纳-辛钦定理将其变换到频域, 并整理可得频域正则维纳滤波器为:

$\begin{matrix} W_{r} (f) = \frac{P_{xx} (f) - P_{vv} (f)}{P_{xx} (f) + α P_{vv} (f)} (7) \end{matrix}$

式中:P_vv(f)和P_xx(f)分别为v(n)和x(n)的自功率谱; W_r $\begin{matrix} (f) \end{matrix}$ 是w_r $\begin{matrix} (n) \end{matrix}$ 的频域形式。

式(7)中利用了在信号和噪声不相关的条件下P_dx $\begin{matrix} (f) \end{matrix}$ =P_dd $\begin{matrix} (f) \end{matrix}$ 的特性。由式(4)可以得到传统维纳滤波器的频域形式为:

$\begin{matrix} W (f) = \frac{P_{xx} (f) - P_{vv} (f)}{P_{xx} (f)} (8) \end{matrix}$

通过对比式(7)和(8)可以看出, 正则维纳滤波器与传统频率维纳滤波器相比, 分母增加了α P_vv $\begin{matrix} (f) \end{matrix}$ 这一项, 它是式(5)中附加噪声约束项α E{ $\begin{matrix} [w_{r} {(n) \times v (n)]}^{2} \end{matrix}$ }后的频域体现, 使滤波后噪声均方值达到最小, 实现对噪声的进一步压制。

此外, 本文还引入了信号幅度调节因子, 分别作用于滤波系数中的信号功率谱和噪声功率谱, 使滤波造成的有效信号衰减和噪声压制程度之间达到平衡。首先将式(5)中的目标函数添加信号幅度保持项E{ $\begin{matrix} [d - w_{r} {(n) \times d]}^{2} \end{matrix}$ }, 并利用信号幅度调节因子β 对其进行加权:

$\begin{matrix} \begin{matrix} ξ_{r} (n) = E \{[d (n) - w_{r} {(n) \times x (n)]}^{2}} + \\ αE \{[w_{r} {(n) \times v (n)]}^{2}} + \\ βE \{[d - w_{r} {(n) \times d]}^{2}} (9) \end{matrix} \end{matrix}$

式中:E{[w_r $\begin{matrix} (n) \end{matrix}$ × v $\begin{matrix} (n) \end{matrix}$ ]²}为噪声约束项; E{[d-w_r $\begin{matrix} (n) \end{matrix}$ × d]²}为信号幅度保持项。

整理得到最终的频域正则维纳滤波器为:

W_r $\begin{matrix} (f) \end{matrix}$ = $\begin{matrix} \frac{P_{xx} (f) - P_{vv} (f)}{P_{xx} (f) + α P_{vv} (f) - β P_{dd} (f)} \end{matrix}$ (10)

从式(10)可以看出, 约束项及其正则因子与信号幅度调节因子可以调节信号损失与噪声压制之间的关系, 在有效压制噪声的同时, 使有效信号的成分受到很好的保护。

正则因子α 和信号幅度调节因子β 的选取是一个关键问题, 选取合适的α 和β 值, 使其达到完美组合, 使W_r(f)中有效信号部分得到增强, 噪声部分得到削弱, 增强的有效信号部分弥补滤波造成的幅度衰减, 从而实现对含噪信号的最优滤波。首先, 正则因子α 及幅度保持因子β 越大, 对噪声谱的压制或对信号幅度的保持越强, 反之亦然; 通常α 的取值范围为0< α < 1, 1< β < 2。通过反复试验, 最终得到当α =0.8和β =1.1时为最优组合, 去噪效果及有效信号幅度保持最佳。

由前面推导得出的滤波系数可知, 频域正则维纳滤波器的求解需要已知含噪信号功率谱和噪声功率谱。含噪信号功率谱可以直接通过含噪信号的傅里叶变换计算得到, 而噪声功率谱分为两种情况:①对于合成地震记录, 由于含噪信号中的噪声是已知的, 噪声的傅里叶功率谱可以通过计算加入噪声的傅里叶变换得到; ②对于实际地震资料, 理想的噪声或有效信号是未知的, 需要通过一定的算法进行估计得到。本文充分利用了已知噪声和含噪信号的统计信息, 利用含噪信号傅里叶幅度谱的高频部分及初至前噪声傅里叶幅度谱的低频部分, 实现对噪声傅里叶幅度谱的有效估计。

图1给出了含噪信号和初至前噪声记录的功率谱, 其中f_p表示截止频率。在图1(a)的含噪信号谱中, 高于截止频率的功率谱可看成是噪声功率谱的高频段估计, 而低于截止频率的功率谱由有效信号功率谱和噪声功率谱共同组成, 不能直接得到噪声功率谱。于是利用图1(b)的初至前噪声功率谱中低于对应截止频率的功率谱作为噪声功率谱低频部分的估计, 将两者相结合作为整个频段噪声谱的估计。由于含噪信号高频段几乎不存在有效信号频谱成分, 且初至前部分也几乎不含有效信号, 两部分谱都可认为是纯噪声谱, 因此利用该方法实现对噪声谱的估计更准确, 更接近含噪信号中包含的实际噪声谱值。

	Figure Option View Download New Window
	图1 噪声谱估计示意图Fig.1 Diagrams of noise spectrum estimation

3 试验结果

3.1 合成地震记录

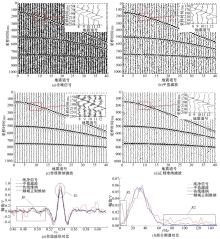
首先, 采用雷克子波, 时间采样间隔为1 ms, 道间距为30 m, 生成含有三个反射同相轴, 每道有1024个采样点的40道合成地震记录。三个同相轴的主频分别为45、35、30 Hz, 层速度分别为1500、1800、2500 m/s。加入高斯白噪声后的含噪地震记录信噪比为-5 dB, 如图2(a)所示。对该含噪记录分别采用中值滤波、传统维纳滤波和频域正则维纳滤波进行噪声压制, 去噪结果如图2(b)(c)(d)所示。

	Figure Option View Download New Window
	图2 合成地震记录效果图Fig.2 Results of synthetic record

从图中可以看出, 三种方法都能去除随机噪声, 使同相轴变得清晰; 但是相比之下, 频域正则维纳滤波处理后残留的背景噪声明显少于中值滤波和传统维纳滤波处理后残留的背景噪声。此外, 从右上角的局部放大图也可以看出, 频域正则维纳滤波后的信号比中值滤波和传统维纳滤波后信号平滑。为了更清楚地比较三种滤波方法的处理效果, 分别从图2(b)(c)(d)的多道数据中各取出一道, 对比单道时域波形和频谱, 如图2(e)(f)所示。

从图2(e)的时域波形中R1区域可见, 传统维纳滤波后的信号仍有小幅振动, 而频域正则维纳滤波后的信号相对平滑, 进一步表明频域正则维纳滤波的去噪效果优于传统维纳滤波。在有效信号保持方面, 从E1区域可以看出, 传统维纳滤波处理后的信号幅值有所降低, 而频域正则维纳滤波处理后的信号幅值得到了有效保持, 由此证明与传统维纳方法相比, 频域正则维纳在有效信号幅度保持方面也具有明显优势。

观察图2(f)中的频谱图可知, 对于R1区域内10 Hz以下的低频谱部分, 频域正则维纳较传统维纳压制效果稍好些, 10 Hz到80 Hz的频谱部分频域正则维纳比传统维纳滤波对频率成分保持完好, 而对于R2区域内70 Hz以上的高频谱部分, 与传统维纳方法相比, 频域正则维纳滤波后噪声压制更理想。

表1给出了三种滤波方法处理前后, 信号在信噪比、幅度衰减和偏差方面的相关数据。由这些频域正则维纳滤波与中值滤波和传统维纳滤波相比:①频域正则维纳滤波后信噪比(SNR)较中值滤波提高了3.1319 dB, 比传统维纳滤波提高了4.4516 dB, 表明频域正则维纳滤波对噪声的压制效果优于中值滤波和传统维纳滤波; ②在有效信号保持方面, 频域正则维纳滤波处理后信号幅度衰减比中值滤波处理后减少了约5.9916%, 比传统维纳滤波处理后减少了约3.1061%, 表明频域正则维纳滤波在有效信号保持方面也优于中值滤波和传统维纳滤波; ③在滤波后信号偏差方面, 频域正则维纳滤波后信号偏差比中值滤波减少了3.7515, 比传统维纳滤波后信号减少了3.9828。这些数据充分表明了频域正则维纳滤波在噪声压制和有效信号保持方面较中值滤波和传统维纳滤波的优越性。

表1 三种滤波方法去噪效果比较 Table 1 Comparison of results of three methods

3.2 实际地震记录

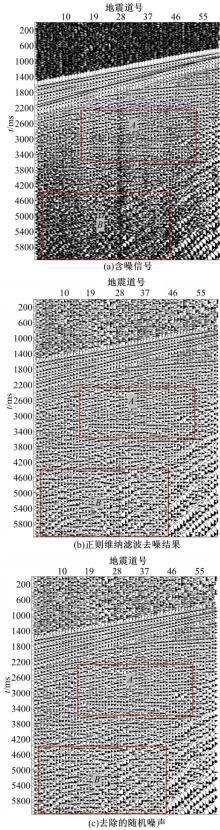
图3(a)为某地区的一张60道, 每道6145点的共炮点地震记录, 其采样频率为1000 Hz。图3(b)(c)分别为频域正则维纳滤波的处理结果及滤除的噪声。从图3(a)可见, 样本中不仅存在随机噪声, 还有直流干扰噪声, 且左下角B区域随机噪声较强, 信噪比较低。

	Figure Option View Download New Window
	图3 实际地震资料Fig.3 Results of actual seismic signal

图3(b)中A区的颜色明显变浅, 随机噪声得到有效压制。此外, 图3(b)中B区的效果表明了正则维纳滤波对于低信噪比情况下的随机噪声有有效的压制, 同相轴变得清晰易见。观察图3(c)中的噪声可以看出, 对有效信号的损害不是很强, 只在初至附近有些影响, 也就是说有效信号的损失有限。

4 结束语

针对强噪声低信噪比背景条件下, 传统维纳滤波方法在地震勘探噪声压制过程中存在的一些缺陷, 提出了一种频域正则化维纳滤波方法。新方法中频域滤波系数的求取过程避免了时域中存在的适应性变差、滤波系数矩阵求解“ 病态” 等问题, 并利用初至前噪声和含噪信号实现对噪声功率谱的有效估计, 并且该方法不依赖有效信号的先验信息。Ricker子波仿真试验结果表明, 频域正则化维纳滤波与中值滤波和传统维纳滤波相比, 信噪比提高、有效信号的幅度衰减减小, 信号偏差降低; 实际地震记录处理结果表明, 与传统维纳滤波相比, 频域正则化维纳滤波在降噪的同时较好地保持了有效频率成分, 同相轴变得清晰易见, 且对直流干扰有一定的压制效果; 频域正则化维纳滤波方法实现简单, 运算速度快, 可以在有效信号和噪声特性未知的条件下进行降噪处理, 具有很强的实用价值。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	付燕. 人工地震信号去噪方法研究[D]. 西安: 西北工业大学计算机学院, 2002. Fu Yan. Research on de-noising methods of seismic data[D]. Xi'an: School of Computer Science, Northwestern Polytechnical University, 2002. [本文引用:1]
[2]	张军华, 吕宁, 田连玉, 等. 地震资料去噪方法、技术综合评述[J]. 地球物理学进展, 2005, 20(4): 1083-1091. Zhang Jun-hua, Lü Ning, Tian Lian-yu, et al. An overview of the methods and techniques for seismic data noise attenuation[J]. Progress in Geophysics, 2005, 20(4): 1083-1091. [本文引用:1]
[3]	Li Y, Yang B J, Badal J, et al. Chaotic system detection of weak seismic signals[J]. Geophysical Journal International, 2009, 178(3): 1493-1522. [本文引用:1]
[4]	崔若飞, 王辉. 多项式拟合技术在煤田地震勘探中的应用[J]. 地球物理学进展, 2000, 15(2): 47-54. Cui Ruo-fei, Wang Hui. Application of polynomial fitting technique on coal seismic surveying[J]. Progress in Geophysics, 2000, 15(2): 47-54. [本文引用:1]
[5]	李英, 张淑贞, 许康生. 小波降噪方法在地震信号处理中的应用[J]. 西北地震学报, 2006, 28(2): 159-162. Li Ying, Zhang Shu-zhe, Xu Kang-sheng. Application of wavelet transfer in seismic signal denoise[J]. Northwestern Seismological Journal, 2006, 28(2): 159-162. [本文引用:1]
[6]	高静怀, 毛剑, 满蔚仕, 等. 叠前地震资料噪声衰减的小波域方法研究[J]. 地球物理学报, 2006, 49(4): 1155-1163. Gao Jing-huai, Mao Jian, Man Wei-shi, et al. On the denoising method of prestack seismic data in wavelet domain[J]. Chinese Journal of Geophysics, 2006, 49(4): 1155-1163. [本文引用:1]
[7]	李月, 林红波, 杨宝俊, 等. 强随机噪声条件下时窗类型局部线性化对TFPF技术的影响[J]. 地球物理学报, 2009, 52(7): 1899-1906. Li Yue, Lin Hong-bo, Yang Bao-jun, et al. The influence of limited linearization of time window on TFPT under the strong noise background[J]. Chinese Journal of Geophysics, 2009, 52(7): 1899-1906. [本文引用:1]
[8]	张洁, 李月. 平行径向道时频峰值滤波消减地震资料的随机噪声[J]. 吉林大学学报: 工学版, 2014, 44(3): 882-887. Zhang Jie, Li Yue. Reduction of rand om noise in seismic data by parallel radial-trace time-frequency peak filtering[J]. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(3): 882-887. [本文引用:1]
[9]	Chen J D, Benesty J, Huang Y A. New insights into the noise reduction wiener filter[J]. IEEE Transactions on Audio, Speech and Language Processing, 2006, 14(4): 1218-1233. [本文引用:1]
[10]	Sekko E, Thomas G, Boukrouche A. A deconvolution technique using optimal Wiener filtering and regularization[J]. Signal Processing, 1999, 72(1): 23-32. [本文引用:1]
[11]	姚天任, 孙洪. 现代数字信号处理[M]. 武汉: 华中科技大学出版社, 1999. [本文引用:1]
[12]	王岩, 梁甸农, 郭汉伟. 基于改进正则化方法的SAR图像增强技术[J]. 电子学报, 2003, 31(9): 1307-1309. Wang Yan, Liang Dian-nong, Guo Han-wei. SAR image enhancement using modified regularization method[J]. ACTA Electronica Sinica, 2003, 31(9): 1307-1309. [本文引用:1]
[13]	Arslan L M. Modified wiener filtering[J]. Signal Processing, 2006, 86(2): 267-272. [本文引用:1]
[14]	Vaseghi S V. 现代数字信号处理与噪声降低[M]. 邱天爽译. 3版. 北京: 电子工业出版社, 2007. [本文引用:1]

2002

0.0

... 如何提高地震资料的信噪比一直是人们关注的问题^[1,2] ...

2005

0.0

. 2005, 20(4):1083-1091

An overview of the methods and techniques for seismic data noise attenuation

地震资料去噪方法、技术综合评述

Zhang Jun-hua , L#cod#x000fc; Ning , Tian Lian-yu

张军华, 吕宁, 田连玉

For both prestack seismic gathers and stacked seismic data, noise attenuation is a very important part of seismic data processing. With the advancement of exploration techniques, the accumulated and developed software for noise attenuation are becoming more and more. It is valuable in theory and instructional in practice to sort different methods of noise attenuation and state their fundamentals, physical meanings, applied conditions and development futures. In this paper, we firstly divide the noise in seismic data according to different characteristics, and then overview some popular methods of noise attenuation in practice, including frequency filtering, frequency-wavenumber filtering, frequency-space filtering, the Radon transform, beamforming, methods of noise attenuation on the basis of wavelet decomposition and reconstruction, and so on. In the end, we also talk about the development trend of techniques for noise attenuation.

地震资料去噪，无论是叠前还是叠后，都是处理中非常重要的内容.随着勘探技术的进步，地球物理界积累和开发的去噪软件已越来越多.对各种去噪方法进行分门别类，阐述其基本原理、物理意义、适用条件、发展前景，既有理论价值又有实际指导意义.本文从噪声的特征出发，首先对地震资料噪声进行了分类；然后综合评述了目前实际生产中常用的几种去噪方法，包括频率域滤波、频率波数域滤波、频率空间域滤波、Radon变换、聚束滤波、基于小波分解和重建的去噪方法等；最后还简述了去噪技术的应用及发展情况.

... 如何提高地震资料的信噪比一直是人们关注的问题^[1,2] ...

2009

0.0

... 已经有许多压制随机噪声的成熟方法,如中值滤波^[3]、多项式拟合^[4]、小波变换^[5,6],时频峰值滤波^[7]和维纳滤波^[8,9]等 ...

2000

0.0

. 2000, 15(2):47-54

Application of polynomial fitting technique on coal seismic surveying

多项式拟合技术在煤田地震勘探中的应用

Cui Ruo-fei , Wang Hui.

崔若飞, 王辉

China University of Mining and Technology,Xuzhou 221008 China

In this paper,application of three polynomial fitting methods,which can eliminate the stretching of NMO correction and low pass effect of stacking,and keep true amplitude and higher frequency of seismic data,is discussed im coal seismic surveying. Zero offset profile with higher resolution can be oltainde by polynomial fitting methods, which is helpful to structural interpretation and lithologic research of seismic data.

本文讨论了三种多项式拟合方法在煤田地震勘探中的应用情况．它们可以消除动校拉伸对波形的影响以及普通叠加的低通滤波效应，保持了振幅的真实形态和较高的频率信息，能得到较高分辨率的零炮检距剖面，有利于地震资料的构造解释和岩性研究．

... 已经有许多压制随机噪声的成熟方法,如中值滤波^[3]、多项式拟合^[4]、小波变换^[5,6],时频峰值滤波^[7]和维纳滤波^[8,9]等 ...

2006

0.0

... 已经有许多压制随机噪声的成熟方法,如中值滤波^[3]、多项式拟合^[4]、小波变换^[5,6],时频峰值滤波^[7]和维纳滤波^[8,9]等 ...

2006

0.0

. 2006, 49(4):1155-1163

On the denoising method of prestack seismic data in wavelet domain

叠前地震资料噪声衰减的小波域方法研究

Gao Jing-huai , Mao Jian , Man Wei-shi

高静怀, 毛剑, 满蔚仕

1 Institute of Wave and Information，School of Electronic and Information Engineering, Xi'an Jiaotong University, Xi'an 710049, China 2 College of Information Science and Engineering, Wuhan University of Science & Technology, Wuhan 430081, China

The modeling of the random noise in prestack seismic data is discussed. The statistic character of the local wavelet power spectrum of the random noise is studied by qualitative analysis and Monte Carlo simulation using physical wavelet. A conclusion is drawn that the distribution of the local wavelet power spectrum of the noise is χ22. On the basis of the conclusion, a method of determing the area of the useful signal energy distribution in wavelet domain is given and the noise is restrained by reconstruction of the signal from the area. The validity of the method is proved by calculations of a model and real seismic data.

讨论了叠前地震记录中随机噪声的模拟方法，采用定性分析与Monte Carlo仿真相结合的方法，研究了在物理小波为基本小波的变换域该类随机噪声局部小波功率谱的统计特性，得出：其局部小波功率谱服从χ22分布.在此基础上，利用假设检验给出了在给定置信度下确定有效信号在小波变换域内能量分布空间的方法，通过在有效信号能量分布空间重建信号来压制噪声.给出了模型及实际地震资料算例，证明了本文提出的方法的有效性.

... 已经有许多压制随机噪声的成熟方法,如中值滤波^[3]、多项式拟合^[4]、小波变换^[5,6],时频峰值滤波^[7]和维纳滤波^[8,9]等 ...

2009

0.0

. 2009, 52(7):1899-1906 DOI:10.3969/j.issn.0001-5733.2009.07.025

The influence of limited linearization of time window on TFPT under the strong noise background

强随机噪声条件下时窗类型局部线性化对TFPF技术的影响

Li Yue , Lin Hong-bo , Yang Bao-jun

李月, 林红波, 杨宝俊

1 Department of Information Engineering, Jilin University,Changchun 130012,China 2 Department of Geophysics, Jilin University,Changchun 130026,China 3 Department of Geology ,Jilin University,Changchun 130061,China 4 Department of Telecommunication Engineering, Changchun University of Science and Technology 130022,China

Time-frequency peak filtering (TFPF) method is a staple technique for eliminating strong random noise in seismic exploration data. For applying these techniques extensively, this paper discussed the details of application of this method, such as choice of the length of time window, local linearization in one time window, etc. For the results of the simulation of time-varying time window TFPF, we compare many values, including the strength of global background, the amplitude of spectrum, signal-to-noise ratio, mean square error, the amplitude of peak/valley of valid wavelet, and the degree of the aberrance of wavelets, and then conclude synthetically that time-windowing filtering ( L 0 + L x ) will get rather ideal effect. In the case of triangle waves, the filtering effect of TFPF is related to the average curvature of side line, the length of time window, etc. The bigger the average curvature of side line is, the bigger the mean square error is; moreover, increasing the average curvature of side line will cause a trend of decreasing in the chosen length of time window. In conclusion, applying TFPF method for eliminating random noise in seismic exploration, suitable parameter of time window should be chosen, on the other hand, the parameter of time window should not vary too much, so the waveform of valid wavelet is not distorted.

为了更广泛地应用时频峰值滤波方法消减地震勘探记录中强随机噪声，本文比较详细地探讨了该方法在应用时需要处理的时窗选取、一个时窗内局部线性化等主要基础技术问题.经过时变时窗的仿真计算，运用多项指标比较，包括整体背景强弱、振幅谱、信噪比、均方误差、有效子波波峰波谷幅值、畸变程度，综合评价出（ L 0 + L x ）时窗滤波的效果较理想.对于三角波这类简单类型的周期波，其时频峰值滤波效果与边线段平均曲率变化、时窗长度等条件有关，即三角波边线段平均曲率越大，滤波结果的均方误差越大；另外，边线段平均曲率增大时，选取的时窗长度有变小的趋势.总之，在地震勘探中应用时频峰值滤波方法消减强随机噪声时，一方面要合理地选取时窗参数，另一方面时窗参数又不能变化过大，以避免对有效子波波形产生畸变影响.

... 已经有许多压制随机噪声的成熟方法,如中值滤波^[3]、多项式拟合^[4]、小波变换^[5,6],时频峰值滤波^[7]和维纳滤波^[8,9]等 ...

2014

0.0

. 2014, 44(3):882-887 DOI:10.13229/j.cnki.jdxbgxb201403048

Reduction of random noise in seismic data by parallel radial-trace time-frequency peak filtering

平行径向道时频峰值滤波消减地震资料的随机噪声

Zhang Jie , Li Yue.

张洁, 李月

1.College of Communication and Engineering,Jilin University,Changchun 130012,China; 2.Editorial Board of Journal of Jilin UniversityInformation and Science Edition, Changchun 130012, China

Traditional Time-frequency Peak Filtering (TFPF) usually causes errors at peaks and valleys of valid signal. This study proposed a parallel Radial Trace Transform (RTT)-TFPF with x-interpolation method to reduce these errors. The proposed method uses TFPF to eliminate noise after mapping seismic signals from coordinates of offset and traveltime to those of apparent velocity and traveltime, namely filtering the signals along the direction of the radial trace in the time-space domain. The effect of the different slope of radial trace on the unbiased estimation of TFPF was discussed. Simulation experiments of synthetic seismogram were carried out to compare the traditional TFPF and the RTT-TFPF with different slopes. The results show that when the selected radial traces and events are parallel or the angles between them are small, the proposed method can make the signals better meet the condition of unbiased estimation in one window length, reduce the errors of the peaks and valleys of filtered signal, and improve the property of amplitude-preservation, the SNR of the proposed method can increase about 5 dB.

针对传统时频峰值滤波(TFPF)算法在消减地震勘探资料中的随机噪声时,容易引起有效信号波峰和波谷处的误差问题,提出了平行径向道TFPF方法。该方法将地震信号从炮检距-双程旅行时域变换到视速度-双程旅行时域后,沿时空域径向道方向进行TFPF。讨论了不同径向道轨线对TFPF无偏估计的影响,并对人工合成的地震记录进行了仿真试验,将沿不同轨线的平行径向道TFPF与传统TFPF结果进行比较。结果表明:所选轨线平行于同相轴或与之夹角很小时,可使信号在一个TFPF时窗内更好地满足无偏估计的条件,从而减小了滤波后波峰及波谷处的误差,使本文方法具有更好的保幅性,其信噪比较传统TFPF算法提高了5 dB左右,通过对实际地震记录的仿真,证明了该方法的实用性。

... 已经有许多压制随机噪声的成熟方法,如中值滤波^[3]、多项式拟合^[4]、小波变换^[5,6],时频峰值滤波^[7]和维纳滤波^[8,9]等 ...

2006

0.0

... 已经有许多压制随机噪声的成熟方法,如中值滤波^[3]、多项式拟合^[4]、小波变换^[5,6],时频峰值滤波^[7]和维纳滤波^[8,9]等 ...

1999

0.0

... 维纳滤波器是以最小均方差为约束准则的最佳匹配滤波器,在地震勘探领域中可应用于含噪地震记录的解卷积^[10] ...

1999

0.0

... 所谓正则化方法是指在求解过程中,用原始数据和噪声的先验知识对解加以约束,从而获得最佳解^{[11,12,13,14]} ...

2003

0.0

... 所谓正则化方法是指在求解过程中,用原始数据和噪声的先验知识对解加以约束,从而获得最佳解^{[11,12,13,14]} ...

2006

0.0

... 所谓正则化方法是指在求解过程中,用原始数据和噪声的先验知识对解加以约束,从而获得最佳解^{[11,12,13,14]} ...

2007

0.0

... 所谓正则化方法是指在求解过程中,用原始数据和噪声的先验知识对解加以约束,从而获得最佳解^{[11,12,13,14]} ...