基于不同时延业务的中继正交频分复用系统资源分配算法

引用本文

赵晓晖, 杨伟伟, 金晓光. 基于不同时延业务的中继正交频分复用系统资源分配算法. 2015, 45(6): 2049-2055
ZHAO Xiao-hui, YANG Wei-wei, JIN Xiao-guang. Resource allocation algorithm for different delay traffic in relay-based OFDM systems. Journal of Jilin University Engineering and Technology Edition, 2015, 45(6): 2049-2055 复制到剪切板

Permissions

基于不同时延业务的中继正交频分复用系统资源分配算法

赵晓晖, 杨伟伟, 金晓光

吉林大学通信工程学院,长春 130012

作者简介:赵晓晖(1957-),男,教授,博士生导师.研究方向:信号处理理论在通信中的应用.E-mail:xhzhao@jlu.edu.cn

基金:国家自然科学基金项目(61171079)

摘要

针对同时包含有时延约束(DC)用户和没有时延约束(NDC)用户的异构系统资源分配问题,在基站和中继站功率分别约束的条件下,为保证DC用户的固定数据速率,同时最大化NDC用户的总数据速率,提出了一种自适应资源分配算法。该算法在子载波分配过程中,考虑了两跳中继链路子载波配对和不配对两种情况,在功率分配过程中,实现了最优功率分配。仿真结果表明,本文提出的资源分配算法可以在较低计算复杂度下取得良好性能。

关键词: 信息处理技术; 中继通信系统; 资源分配; 有时延约束; 无时延约束

中图分类号:TN929 文献标志码:A 文章编号:1671-5497(2015)06-2049-07

Resource allocation algorithm for different delay traffic in relay-based OFDM systems

ZHAO Xiao-hui, YANG Wei-wei, JIN Xiao-guang

College of Communication Engineering, Jilin University, Changchun 130012, China

Abstract

In order to solve resource allocation problem in heterogeneous system with Delay-Constrained (DC) users and No-Delay-Constrained (NDC) users, under the power constraints for base station and relay stations to guarantee data rates for DC users and with the maximization of the sum-rate of NCD users, an adaptive allocation algorithm is proposed. In the subcarrier allocation, both subcarrier matching and non-matching of two-hop relay links are considered. In the power allocation, optimal power allocation is obtained. Simulation results show that the proposed resource allocation algorithm has better performance with lower computation complexity.

Keyword: information processing; resource allocation; relay-assisted communication systems; delay constrain; non-delay constrain

Show Figures

0 引言

在宽带移动通信应用中, 传输信号在无线信道中遇到了多径频率选择性衰落的问题, 导致了严重的符号间干扰(ISI), 对系统的通信服务质量和数据传输速率都产生了严重的影响。正交频分复用(OFDM)技术以其频谱利用率高、抗多径时延能力强、可以有效消除符号间干扰等优点在业界得到了广泛的应用^[1]。在传统OFDM系统中, 资源分配技术已经比较成熟^{[2, 3, 4]}, 但其吞吐量相对较低, 无法满足用户对数据速率快速增长的需求。中继技术因其能够有效地提高系统的吞吐量, 扩展小区覆盖范围, 已经成为下一代无线通信领域研究的热点。在传统OFDM系统中引入中继技术后, 系统的链路发生了变化, 使得质量较差的一跳链路可以被分割为多个质量较好的多跳链路, 这两种关键技术的结合可以获得更好的系统性能。

目前, 对OFDM中继网络的资源分配问题的研究已经取得了一些研究成果^{[5, 6, 7, 8]}。对于两跳的中继网络, 信道的传输特性在第一跳和第二跳中可能会相差很大, 这样就会限制系统的容量。文献[5]通过对两跳链路子载波配对来提高系统的性能。文献[6]在基站和中继站功率分别约束的条件下, 通过对功率分配来最大化系统容量。文献[7]考虑了用户间公平性的问题, 以最大化系统公平性为目标, 在中继OFDM系统中引入了MAX-MIN算法。然而, 在实际通信系统中, 用户的业务需求不同, 最大化系统公平性是不符合实际的。为了满足用户间不同数据速率的要求, 文献[8]提出了一种成比例公平约束的资源分配方案, 这种算法不仅满足了用户对速率的需求, 而且由于引入中继技术, 系统的容量也明显增加。

在以往的资源分配算法中, 大多数算法都专注于一致的约束条件^{[9, 10]}。然而在实际通信系统中, 用户的需求各不相同, 可能同时存在有时延约束和无时延约束的情况^{[11, 12]}。为了更好地满足用户需求, 本文在中继OFDM系统下行链路中研究了一种约束条件不一致的资源分配算法, 这种算法同时包含这两种约束条件。它的目标就是在基站和中继站功率分别约束的条件下, 最大化无时延用户的总数据速率, 同时保证有时延用户的固定数据速率。该算法在子载波分配过程中, 分别考虑子载波配对和不配对两种情况, 在功率分配过程中, 为了利于系统实现, 降低计算复杂度, 提出了一种启发式功率分配算法。仿真结果表明:本文提出的这种优化算法能够保证用户不同时延的服务质量要求, 降低时延约束(DC)用户达到固定数据速率时的功率, 并且能够有效地提高系统容量。

1 系统模型

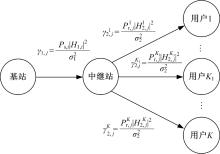
图1为含有中继的多用户OFDM系统下行链路系统模型。此系统包含一个基站BS, 单个中继节点, K个用户。其中, 前K₁个用户受时延约束, 其余的K-K₁个用户无时延约束。中继模式为放大转发方式(AF), 中继节点采用半双工方式, 将一帧分成两个等长的时隙, 在第一个时隙, 基站通过广播方式将数据传输到中继节点; 在第二个时隙, 中继节点对接收到的信号进行适当放大并转发给用户。

	Figure Option View Download New Window
	图1 系统模型Fig.1 System model

在实际通信系统中, 用户通常不能与基站直接进行通信, 如IEEE 802.16j中定义的非透明中继网络^[13]。在该网络中, 中继站的主要作用在于扩展小区的覆盖范围, 此时小区边缘的用户将处在基站的覆盖范围之外, 这些用户只能通过中继站来与基站通信。本文使用类似IEEE 802.16j提出的非透明中继系统模型, 在此模型中, 用户不能直接与基站通信。假定整个系统模型中, 基站、中继站和用户都能获得理想的信道状态信息(CSI)。

设基站发送的信号为X_s; 系统总带宽为B, 并且被分成N个正交子信道。H_1,_i表示第一跳链路上第i个子载波的信道增益; $\begin{matrix} H_{2, j}^{k} \end{matrix}$ 表示第二跳链路上第k个用户在第j个子载波上的信道增益。基站和中继站的功率约束分别是P_s和P_r。α _i表示第一跳链路第i个子载波经中继传输时的放大因子, 为了满足传输功率约束, 放大因子必须满足:

$\begin{matrix} α_{i} \leq \sqrt{\frac{P_{r, j}^{k}}{P_{s, i} {|H_{1, i}|}^{2} + σ_{1}^{2}}} \end{matrix}$

式中:P_s,_i、 $\begin{matrix} P_{r, j}^{k} \end{matrix}$ 分别为基站在子载波上分配的功率和中继到用户k链路上第j个子载波上分配的功率。

假设中继站和目标节点接收到的噪声均为加性高斯白噪声(AWGN), 且AWGN的功率谱密度在两跳链路所有子载波上都是相等的, 分别用 $\begin{matrix} σ_{1}^{2} \end{matrix}$ 和 $\begin{matrix} σ_{2}^{2} \end{matrix}$ 表示第一跳链路和第二跳链路每个子载波上的AWGN。第一跳链路第i个子载波的信号经过中继转发到第二跳链路第j个子载波, 并且传送给用户k的信号可以表示为:

$\begin{matrix} Y_{j}^{k} = α_{i} H_{2, j}^{k} H_{1, i} X_{s} + α_{i} H_{2, j}^{k} σ_{1}^{2} + σ_{2}^{2} (1) \end{matrix}$

定义γ _1,_i=P_s,_i $\begin{matrix} {|H_{1, i}|}^{2} \end{matrix}$ / $\begin{matrix} σ_{1}^{2} \end{matrix}$ 为第一跳链路第i个子载波的信噪比, $\begin{matrix} γ_{2, j}^{k} \end{matrix}$ = $\begin{matrix} P_{r, j}^{k} \end{matrix} \begin{matrix} {|H_{2, j}^{k}|}^{2} \end{matrix}$ / $\begin{matrix} σ_{2}^{2} \end{matrix}$ 为中继到用户k链路第j个子载波的信噪比。为了使符号简化, 令:

a_1,_i= $\begin{matrix} \frac{{|H_{1, i}|}^{2}}{σ_{1}^{2}} \end{matrix}$ ; $\begin{matrix} b_{2, j}^{k} \end{matrix}$ = $\begin{matrix} \frac{{|H_{2, j}^{k}|}^{2}}{σ_{2}^{2}} \end{matrix}$ 。

在AF中继模式下, 用户k在使用第一跳链路第i个子载波和第二跳链路第j个子载波组成的中继链路进行传输时, 该链路上的数据传输速率可以表示为:

$\begin{matrix} R_{i, j}^{k} = \frac{B}{2 N} lo g_{2} (1 + f (γ_{1, i}, γ_{2, j}^{k})) (2) \end{matrix}$

式中:f定义为:

$\begin{matrix} f (x, y) = \frac{xy}{1 + x + y} (3) \end{matrix}$

用户k获得的数据速率为:

$\begin{matrix} \begin{matrix} R_{k} = \overset{N}{\sum_{j = 1}} ρ_{k, j} \overset{N}{\sum_{i = 1}} ω_{i, j}^{k} R_{i, j}^{k} = \\ \frac{B}{2 N} \overset{N}{\sum_{j = 1}} ρ_{k, j} \overset{N}{\sum_{i = 1}} ω_{i, j}^{k} [lo g_{2} (1 + f (γ_{1, i}, γ_{2, j}^{k}))] (4) \end{matrix} \end{matrix}$

式中:ρ _k_,_j为第二跳链路上的载波分配, ρ _k_,_j=1表示第二跳链路第j个子载波分配给用户k; $\begin{matrix} ω_{i, j}^{k} \end{matrix}$ 为两跳链路上子载波配对的情况, $\begin{matrix} ω_{i, j}^{k} \end{matrix}$ =1表示第一跳第i个子载波与第二跳第j个子载波配对。

本文研究的是不同时延约束条件下中继网络的资源分配问题。系统中包括K个移动用户, 其中前K₁个用户有时延约束, 即每个用户需要有一个固定的传输速率R'_k(k=1, 2, …, K₁), 剩下的K-K₁个用户没有时延约束, 但需要保证这些用户具有最大的总传输速率。假定第一跳链路某个子载波传输的信息只能通过第二跳链路的一个子载波传送。这类问题的数学模型可以表示为:

$\begin{matrix} \begin{matrix} \max_{ρ_{k, j}, ω_{i, j}^{k}} \overset{K}{\sum_{k = K_{1} + 1}} R_{k} \\ s.t. \{\begin{matrix} C_{1} : R_{k} \geq R'_{k}, k = 1, 2, \dots, K_{1} \\ C_{2} : ρ_{k, j}, ω_{i, j}^{k} = \{0, 1\}, \forall i, j, k \\ C_{3} : \overset{K}{\sum_{k = 1}} ρ_{k, j} = 1, \forall j, \overset{K}{\sum_{k = 1}} \overset{N}{\sum_{j = 1}} ω_{i, j}^{k} = 1, \forall i, \\ \overset{K}{\sum_{k = 1}} \overset{N}{\sum_{i = 1}} ω_{i, j}^{k} = 1, \forall j \\ C_{4} : P_{s, i} \geq 0, P_{r, j}^{k} \geq 0, \forall i, j, k \\ C_{5} : \overset{N}{\sum_{i = 1}} P_{s, i} \leq P_{s}, \overset{K}{\sum_{k = 1}} \overset{N}{\sum_{j = 1}} ρ_{k, j} P_{r, j}^{k} \leq P_{r} \end{matrix} (5) \end{matrix} \end{matrix}$

式中:R_k为第k个用户的数据传输速率, k=1, 2, …, K; C₁为K₁个DC用户固定的传输速率; C₂为第二跳链路的每个子载波只能分配给一个用户; C₃为两跳链路的子载波配对分别是一一对应的; C₄和C₅分别为基站和中继站功率的约束条件。

2 资源分配算法

在多用户OFDM系统中, 当每个子载波分配给对其增益最好的用户时, 平坦传输功率谱密度(Flat transmit PSD)几乎不会降低系统的吞吐量^[3]。为此, 本文将子载波和功率分开分配:第1步在功率均等分配的前提下对子载波进行分配; 第2步在给定子载波分配方案的情况下进行功率分配。

2.1 子载波分配算法

假设子载波间功率均等分配, 首先对DC用户进行子载波分配, 然后再对没有时延约束(NDC)用户进行子载波分配。下面分别讨论子载波配对和不配对两种情况下的分配算法。

2.1.1 不考虑子载波配对时的算法

DC用户在不考虑子载波配对时的子载波分配过程如下:

(1)初始化, 令R_k=0, Φ 和Ψ 分别表示第一跳链路和第二跳链路中尚未分配的子载波集合, 而且都被初始化为{1, 2, …, N}, 设Ω _k为第k个用户的子载波集合。

(2)当Φ ≠ ∅, Ψ ≠ ∅, Ω _k=∅, R_k< R'_k, 1≤ k≤ K₁时, ①求解k^*, 使其满足 $\begin{matrix} R_{k^{*}} \end{matrix}$ < R $\begin{matrix} '_{k^{*}} \end{matrix}$ 和 $\begin{matrix} R_{k^{*}} \end{matrix}$ -R $\begin{matrix} '_{k^{*}} \end{matrix}$ ≤ R_k-R'_k, 1≤ k≤ K₁; ②对于已求解的k^*, ∀ n∈ Ψ , 计算满足 $\begin{matrix} |H_{2, j}^{k^{*}}| \end{matrix}$ ≥ $\begin{matrix} |H_{2, n}^{k^{*}}| \end{matrix}$ 的j, 然后在第一跳中选择与其序号相同的子载波, 更新Φ =Φ - $\begin{matrix} \{j\} \end{matrix}$ , Ψ =Ψ - $\begin{matrix} \{j\} \end{matrix}$ , $\begin{matrix} Ω_{k^{*}} \end{matrix}$ = $\begin{matrix} Ω_{k^{*}} \end{matrix}$ ∪ {j}, 更新 $\begin{matrix} R_{k^{*}} \end{matrix}$ 。

上述算法在第(2)步骤的每次迭代中, DC用户中实时速率距离目标速率最大的用户在第二跳的子载波集合中有优先选择信噪比最高子载波的权利。当用户k(1≤ k≤ K₁)获得子载波集合Ω _k后, 再把剩余的子载波分配给K-K₁个NDC用户。而NDC用户子载波分配策略是将第二跳的每一个子载波都分配给对其信道增益最高的用户, 而且只能分配给一个用户, 然后在第一跳中选择与其序号相同的子载波。

2.1.2 考虑子载波配对时的算法

DC用户的子载波分配过程如下:

(1)初始化, 令R_k=0, Φ 和Ψ 分别表示第一跳链路和第二跳链路中尚未分配的子载波集合, 而且都被初始化为{1, 2, …, N}, 设Ω _k为第k个用户的子载波集合;

(2)当Φ ≠ ∅, Ψ ≠ ∅, Ω _k=∅, R_k< R'_k, 1≤ k≤ K₁时, ①求解k^*, 使其满足 $\begin{matrix} R_{k^{*}} \end{matrix}$ < R $\begin{matrix} '_{k^{*}} \end{matrix}$ 和 $\begin{matrix} R_{k^{*}} \end{matrix}$ -R $\begin{matrix} '_{k^{*}} \end{matrix}$ ≤ R_k-R'_k, 1≤ k≤ K₁; ②对于已求解的k^*, ∀ n∈ Ψ , 计算满足 $\begin{matrix} |H_{2, j}^{k^{*}}| \end{matrix}$ ≥ $\begin{matrix} |H_{2, n}^{k^{*}}| \end{matrix}$ 的j, 然后将第一跳链路的子载波按照从高到低的顺序排序, 选择信道增益最高的子载波i与第二跳链路的子载波j进行配对, 更新Φ =Φ - $\begin{matrix} \{i\} \end{matrix}$ , Ψ =Ψ - $\begin{matrix} \{j\} \end{matrix}$ , $\begin{matrix} Ω_{k^{*}} \end{matrix}$ = $\begin{matrix} Ω_{k^{*}} \end{matrix}$ ∪ {j}, 更新 $\begin{matrix} R_{k^{*}} \end{matrix}$ 。

当用户k(1≤ k≤ K₁)获得子载波集合Ω _k后, 再把剩余的子载波分配给K-K₁个NDC用户。NDC用户子载波分配策略是将第二跳链路的每一个子载波都分配给对其信道增益最高的用户, 而且只能分配给一个用户, 然后将第一跳链路中子载波按照从高到低的顺序排序, 选择信道增益最高的子载波与第二跳的子载波进行配对。

2.2 给定子载波分配方案下的功率分配

传统的功率分配算法多数基于假设基站和中继站总功率受约束, 但是这种约束适合于低移动性的无线网络, 而且在联合功率约束条件下传输信号的开销很高, 因此对基站和中继站的功率分开进行约束更可行。对于每种子载波的分配方案, 基站和中继站的功率将被用来满足每个DC用户固定数据速率的需求, 同时最大化NDC用户的总数据速率。在前面子载波分配下进行功率分配, 首先对DC用户分配功率, 然后对NDC用户进行功率分配。可将初始问题转变为:

$\begin{matrix} \begin{matrix} \max \overset{K}{\sum_{k = K_{1} + 1}} R_{k} \\ s.t. \{\begin{matrix} C_{1} : R_{k} \geq R'_{k}, 1 \leq k \leq K_{1} \\ C_{2} : \overset{N}{\sum_{i = 1}} P_{s, i} \leq P_{s} \\ C_{3} : \overset{K}{\sum_{k = 1}} \sum_{j \in Ω_{k}} P_{r, j}^{k} = P_{r} \\ C_{4} : P_{r, j}^{k} \geq 0, P_{s, i} \geq 0, \forall i, j, k \end{matrix} (6) \end{matrix} \end{matrix}$

式中:R_k= $\begin{matrix} \sum_{j \in Ω_{k}} \end{matrix} \begin{matrix} R_{i, j}^{k} \end{matrix}$ = $\begin{matrix} \frac{B}{2 N} \end{matrix} \begin{matrix} \sum_{j \in Ω_{k}} \end{matrix}$ [log₂(1+f(γ _1,_i, $\begin{matrix} γ_{2, j}^{k} \end{matrix}$ ))], 子载波i满足 $\begin{matrix} ω_{i, j}^{k} \end{matrix}$ =1。

上述模型中涉及了连续变量和二进制变量, 这是一个混合整数规划问题, 并不属于凸优化问题。但是, 文献[14]通过数学推导以及仿真证明, 对于一个多载波OFDM系统来说, 当子载波数量足够大时, 即使原问题不是凸优化问题, 其对偶差额仍然为零。所以, 本文根据此结论对最优化(Karush-Kuhn-Tucker, KKT)条件^[15]分别求导。这个问题的拉格朗日函数为:

$\begin{matrix} \begin{matrix} J (\{P_{s, i}\}, \{P_{r, j}^{k}\} λ, β, μ) = \\ \overset{K}{\sum_{k = K_{1} + 1}} R_{k} + \overset{K_{1}}{\sum_{k = 1}} β_{k} [R_{k} - R'_{k}] + \\ λ (P_{s} - \overset{N}{\sum_{i = 1}} P_{s, i}) + μ (P_{r} - \overset{K}{\sum_{k = 1}} \sum_{j \in Ω_{k}} P_{r, j}^{k}) (7) \end{matrix} \end{matrix}$

式中:β =(β ₁, β ₂, …, $\begin{matrix} β_{K_{1}} \end{matrix}$ )≥ 0; μ ≥ 0、λ ≥ 0分别是C₁、C₂、C₃约束条件的拉格朗日乘子; C₄中的边界约束条件包含在KKT条件中, 对于1≤ k≤ K, 1≤ i, j≤ N, 用 $\begin{matrix} P_{s, i}^{*} \end{matrix}$ 和 $\begin{matrix} P_{r, j}^{k*} \end{matrix}$ 来表示最优解。通过KKT条件, 可以获得关 $\begin{matrix} P_{s, i}^{*} \end{matrix}$ 和 $\begin{matrix} P_{r, j}^{k*} \end{matrix}$ 必要充分条件。对于 $\begin{matrix} P_{s, i}^{*} \end{matrix}$ 和 $\begin{matrix} P_{r, j}^{k*} \end{matrix}$ , 应该满足以下条件:

$\begin{matrix} \begin{matrix} \frac{\partial J (\cdot)}{\partial P_{s, i}^{*}} \{\begin{matrix} = 0, P_{s, i}^{*} > 0 \\ < 0, P_{s, i}^{*} = 0 \end{matrix}, \forall k, i (8) \\ \frac{\partial J (\cdot)}{\partial P_{r, j}^{k*}} \{\begin{matrix} < 0, P_{r, j}^{k*} = 0 \\ = 0, P_{r, j}^{k*} > 0 \end{matrix}, \forall k, j (9) \\ β_{k} [R_{k} - R'_{k}] = 0, 1 \leq k \leq K_{1} (10) \end{matrix} \end{matrix}$

(1)在P_s给定的情况下, 求解使目标数据速率最大时的 $\begin{matrix} P_{r, j}^{k} \end{matrix}$ , 用 $\begin{matrix} P_{r, j}^{k*} \end{matrix}$ 来表示。对拉格朗日函数式(7)中的 $\begin{matrix} P_{r, j}^{k} \end{matrix}$ 求导, 把结果代入式(9)中的KKT条件, 可得:

$\begin{matrix} P_{r, j}^{k*} = \frac{1}{b_{2, j}^{k}} {[\frac{P_{s, i} a_{1, i}}{2} (\sqrt{1 + \frac{2 b_{2, j}^{k} β_{k} B}{P_{s, i} a_{1, i} Nμln 2}} - 1) - 1]}^{+} (11) \end{matrix}$

式中:1≤ k≤ K₁; 1≤ i, j≤ N。

$\begin{matrix} P_{r, j}^{k*} = \frac{1}{b_{2, j}^{k}} {[\frac{P_{s, i} a_{1, i}}{2} (\sqrt{1 + \frac{2 b_{2, j}^{k} B}{P_{s, i} a_{1, i} Nμln 2}} - 1) - 1]}^{+} (12) \end{matrix}$

式中:K₁+1≤ k≤ K; 1≤ i, j≤ N, 这里定义(x)⁺=max(0, x)。

(2)在P_r给定情况下, 求解使目标数据速率最大时的P_s,_i, 用 $\begin{matrix} P_{s, i}^{*} \end{matrix}$ 来表示。对拉格朗日函数式(7)中的P_s,_i求导, 把结果代入式(8)中的KKT条件, 可得:

$\begin{matrix} P_{s, i}^{*} = \frac{1}{a_{1, i}} {[\frac{P_{r, j}^{k} b_{2, j}^{k}}{2} (\sqrt{1 + \frac{2 a_{1, i} β_{k} B}{P_{r, j}^{k} b_{2, j}^{k} Nλln 2}} - 1) - 1]}^{+} (13) \end{matrix}$

式中:1≤ k≤ K₁; 1≤ i, j≤ N。

$\begin{matrix} P_{s, i}^{*} = \frac{1}{a_{1, i}} {[\frac{P_{r, j}^{k} b_{2, j}^{k}}{2} (\sqrt{1 + \frac{2 a_{1, i} B}{P_{r, j}^{k} b_{2, j}^{k} Nλln 2}} - 1) - 1]}^{+} (14) \end{matrix}$

式中:K₁+1≤ k≤ K; 1≤ i, j≤ N, 这里定义(x)⁺=max(0, x)。

上述算法在求解拉格朗日乘子时, 计算复杂度增大, 实现困难。为此, 本文提出了一种启发式功率分配算法。为了简化起见, 假定基站和中继站的功率约束条件相同, 即P=P_r=P_s。

(1)选取功率间隔Δ P, 令P'=Δ P。

(2)每个子载波进行等功率分配, 每个子载波功率分配的功率为P'/N, 计算DC用户速率。

(3)如果达不到固定速率, 剔除一个信道条件最差的子载波, 然后对剩余子载波进行等分配功率, 每个子载波分配的功率为P'/(N-1), 重新计算DC用户速率, 如果达不到, 继续剔除子载波, 直到DC用户达到固定速率。

(4)如果所有子载波都被剔除, 仍没有达到DC用户的目标数据速率, 增大功率P'=P'+Δ P, 重复步骤(2), 直到DC用户达到固定速率。

(5)当DC用户达到固定速率时, 可以得到满足条件的最小功率P_min=P'。

(6)将系统剩余功率P-P_min等功率分配给NDC用户。

3 仿真实验及结果分析

本文的仿真结果是通过10 000次蒙特卡洛仿真实验得到的。选择一个6径频率选择性衰落信道, 每径服从独立瑞利分布, 信道功率按指数分布衰减, 衰落因子α =3。误码率设置为10^-5。系统总带宽为1 MHz, 系统中子载波数为64个, 用户数量8, 其中NDC与DC的用户数均为4个。为了简化, 假设本文DC用户固定速率相同, 均设为20 bits/OFDM符号。由于DC用户具有时延约束, 低于固定速率的信息传输是没有意义的, 在表示DC用户数据速率时, 使用R_DC表示4个用户中的最低数据速率。在表示NDC用户数据速率时, 使用R_NDC表示4个用户数据速率总和。

图2为本文提出的算法在子载波分配的迭代过程中DC用户优先级变化的曲线。用户优先级定义为目标数据速率和当前数据速率的差值, 速率差值最大的用户有优先选择最好子载波的权利。从图2中可以看出:用户的优先级交替变化, 随着迭代次数的增加, 差值在不断的减小, 最后将会在零值附近收敛, 最终所有用户的速率都将达到目标速率, 实现DC用户所要求的性能。

	Figure Option View Download New Window
	图2 DC用户子载波分配过程的优先级变化曲线Fig.2 Illustration of priority for subcarrier assignment procedure of DC users

图3为将本文提出的自适应子载波分配算法与两种非自适应子载波分配算法的比较结果。这两种算法中每个子载波的功率均等分配, 子载波固定分配。对第一种算法(FSA), 8个用户平等对待, 为每个用户固定分配8个子载波; 对第二种算法(FSAP), DC用户比NDC用户有优先权, 为每个DC用户固定分配12个子载波, 每个NDC用户分配4个子载波。从图3可以看出:DC用户达到目标速率时, 自适应子载波分配算法所需的功率为8 W, FSAP算法需要13 W, 而FSA算法需要20 W, 可见自适应子载波分配算法所需功率较低, 且当DC用户达到目标数据速率时, NDC用户总数据速率大于其他两种算法得到的相应速率。

	Figure Option View Download New Window
	图3 不同子载波分配算法下的用户速率变化曲线Fig.3 Achievable user rates versus different subcarrier assignment scheme

从图4可以看出:DC用户达到目标数据速率时, 本文提出的子载波配对启发式功率分配算法(matching-HPA)需要功率仅2 W, 子载波配对的等功率算法(matching-EPA)需要功率为7 W, 而子载波不配对的等功率算法(No matching-EPA)需要功率为8 W。可见, 本文提出的matching-HPA自适应资源分配算法性能最好, 在较低的功率条件下, 实现了优先保证DC用户的固定速率, 同时最大化NDC用户总速率的目标。

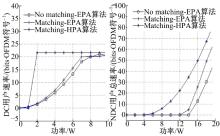	Figure Option View Download New Window
	图4 不同子载波和功率分配算法下的用户速率变化曲线Fig.4 Achievable user rates versus different subcarrier assignment and power allocation schemes

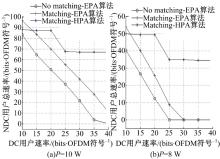
图5给出在不同的DC用户速率约束下, 对图3中所示的3种算法的NDC用户总速率的比较。在基站和中继站功率分别为10 W和8 W两种情况下, 从图5中可以看出, 随着DC用户固定数据速率的增长, NDC用户的数据速率逐渐下降, 原因在于DC用户占用了更多的子载波和功率。功率为8 W时, No matching-EPA算法和matching-EPA算法在DC用户速率为30 bits/OFDM符号时, NDC用户的总速率下降为0, 这表明系统不能正常工作。而采用matching-HPA算法的NDC用户的总速率变化较为缓慢, 具有较强的鲁棒性, 对较大的DC用户速率有更强的承载能力。

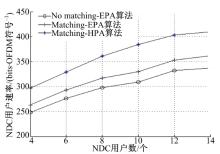
	Figure Option View Download New Window
	图5 NDC用户总数据速率随DC用户数据速率变化的曲线Fig.5 Illustration of achievable R_NDC versus different R_DC

图6为DC用户数量固定为4, NDC用户数量从4变化到16时, NDC用户总速率的变化曲线。可见, 随着NDC用户数量的增加, 由于多用户分集, NDC用户总速率也呈现递增的趋势, 但随着用户数的增大, 这种分集效应会减弱, NDC用户的速率增长变得缓慢, 趋于稳定。综上, 本文提出的matching-HPA算法性能始终优于其他两种算法。

	Figure Option View Download New Window
	图6 NDC用户总速率随NDC用户数变化的曲线Fig.6 Achievable R_NDC versus the number of NDC users

4 结束语

研究了中继OFDM系统下行链路的资源分配问题, 提出了一种同时存在时延和无时延两种约束条件的子载波和功率分配算法, 在子载波分配过程中考虑子载波配对和不配对两种情况, 在功率分配过程中采用了一种低复杂度, 利于系统实现的启发式功率分配算法。仿真结果表明:本文的算法能够保证两种用户不同时延服务的需求, 能够降低DC用户达到目标数据速率时的功率, 同时可以增加NDC用户的总数据速率。由于多用户分集, 在DC用户数量固定时, 随着NDC用户数量的增加, NDC用户的总数据速率也在逐渐增加。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Tong X J, Luo T. Theory and Applications of OFDM Wireless Communications[M]. Beijing: Posts & Telecom Press, 2003. [本文引用:1]
[2]	Jang J, Lee K B. Transmit power adaptation for multi-user OFDM systems[J]. IEEE Journal on Selected Areas in Communications, 2003, 21(2): 171-178. [本文引用:1]
[3]	Rhee W, Cioffi J M. Increase in capacity of multi-user OFDM system using dynamic sub-channel allocation[C]∥Proceedings of IEEE Vehicular Technology Conference, Tokyo, Japan, 2000: 1085-1089. [本文引用:2]
[4]	Shen Z K, Andrews J G, Evans B L. Adaptive resource allocation in multiuser OFDM systems with proportional rate constraints[J]. IEEE Transaction on Wireless Communications, 2005, 4(6): 2726-2737. [本文引用:1]
[5]	Zhou M Y, Li L H, Wang H F, et al. Sub-carrier coupling for OFDM based AF multi-relay systems[C]∥IEEE 18th International Symposium on Personal, Indoor and Mobile Radio Communications, Athens, 2007: 1-5. [本文引用:1]
[6]	Hammerstrom I, Wittneben A. On the optimal power allocation for nonregenerative OFDM relay links[C]∥IEEE International Conference on Communications, Istanbul, 2006: 4463-4468. [本文引用:1]
[7]	Guo J, Luo H W, Li H X. Opportunistic relaying in cooperative OFDM networks for throughput and fairness improvement[C]∥IEEE Global Telecommunications Conference, New Orleans, LO, 2008: 1-5. [本文引用:1]
[8]	Fan B, Wu W, Zheng K, et al. Proportional fair-based joint subcarrier and power allocation in relay-enhanced orthogonal frequency division multiplexing systems[J]. IET Communications, 2010, 4(10): 1143-1152. [本文引用:1]
[9]	Yang D C, Xu J S, Hu S K. Resource allocation for multi-user two-way OFDMA relay networks with user rate constraints[J]. Elsevier Journal of China University of Posts and Telecommunications, 2011, 18(3): 54-61. [本文引用:1]
[10]	Xu W J, He Z Q, Niu K, et al. Multicast resource allocation with min-rate requirements in OFDM systems[J]. Elsevier Journal of China University of Posts and Telecommunications, 2010, 17(3): 24-30. [本文引用:1]
[11]	Lee T H, Huang Y W. Resource allocation achieving high system throughput with QoS support in OFDMA-based system[J]. IEEE Transactions on Wireless Communications, 2012, 60(3): 851-861. [本文引用:1]
[12]	Chen S P, Wang W B, Zhang X, et al. Resource allocation schemes in amplify-and -forward OFDM cooperative relay systems with multi-media traffic[J]. Journal on Communications, 2010, 31(4): 116-121. [本文引用:1]
[13]	IEEE 802. 16j draft-2008. Draft stand ard for local and metropolitan area networks, Part 16: air interface for fixed and mobile broadband wireless access systems, multi-hop relay specification[S]. [本文引用:1]
[14]	Yu W, Lui R. Dual methods for nonconvex spectrum optimization of multicarrier systems[J]. IEEE Transactions on Communications, 2006, 54(7): 1310-1322. [本文引用:1]
[15]	Stephen B, Lieven V. Convex Optimization[M]. Cambridge: Cambridge University Press, 2004. [本文引用:1]

2003

0.0

... 正交频分复用(OFDM)技术以其频谱利用率高、抗多径时延能力强、可以有效消除符号间干扰等优点在业界得到了广泛的应用^[1] ...

2003

0.0

... 在传统OFDM系统中,资源分配技术已经比较成熟^[2,3,4],但其吞吐量相对较低,无法满足用户对数据速率快速增长的需求 ...

2000

0.0

... 在传统OFDM系统中,资源分配技术已经比较成熟^[2,3,4],但其吞吐量相对较低,无法满足用户对数据速率快速增长的需求 ...

... 2 资源分配算法在多用户OFDM系统中,当每个子载波分配给对其增益最好的用户时,平坦传输功率谱密度(Flat transmit PSD)几乎不会降低系统的吞吐量^[3] ...

2005

0.0

... 在传统OFDM系统中,资源分配技术已经比较成熟^[2,3,4],但其吞吐量相对较低,无法满足用户对数据速率快速增长的需求 ...

2007

0.0

... 目前,对OFDM中继网络的资源分配问题的研究已经取得了一些研究成果^[5,6,7,8] ...

2006

0.0

... 目前,对OFDM中继网络的资源分配问题的研究已经取得了一些研究成果^[5,6,7,8] ...

2008

0.0

... 目前,对OFDM中继网络的资源分配问题的研究已经取得了一些研究成果^[5,6,7,8] ...

2010

0.0

... 目前,对OFDM中继网络的资源分配问题的研究已经取得了一些研究成果^[5,6,7,8] ...

2011

0.0

... 在以往的资源分配算法中,大多数算法都专注于一致的约束条件^[9,10] ...

2010

0.0

... 在以往的资源分配算法中,大多数算法都专注于一致的约束条件^[9,10] ...

2012

0.0

... 然而在实际通信系统中,用户的需求各不相同,可能同时存在有时延约束和无时延约束的情况^[11,12] ...

2010

0.0

... 然而在实际通信系统中,用户的需求各不相同,可能同时存在有时延约束和无时延约束的情况^[11,12] ...

0.0

... 16j中定义的非透明中继网络^[13] ...

2006

0.0

2004

0.0

... 所以,本文根据此结论对最优化(Karush-Kuhn-Tucker,KKT)条件^[15]分别求导 ...