稳健的多跳频信号跟踪方法

引用本文

尚佳栋, 王祖林, 周丽娜, 杨蓝. 稳健的多跳频信号跟踪方法. 2015, 45(6): 2056-2061
SHANG Jia-dong, WANG Zu-lin, ZHOU Li-na, YANG Lan. Robust tracking method for multiple frequency-hopping signals. Journal of Jilin University Engineering and Technology Edition, 2015, 45(6): 2056-2061 复制到剪切板

Permissions

稳健的多跳频信号跟踪方法

尚佳栋, 王祖林, 周丽娜, 杨蓝

北京航空航天大学电子信息工程学院,北京 100191

王祖林(1965-),男,教授,博士生导师.研究方向:通信信号处理.E-mail:wzulin@vip.sina.com

作者简介:尚佳栋(1987-),男,博士研究生.研究方向:通信对抗.E-mail:shangjiadong456@163.com

基金:国家自然科学基金项目(61071070)

摘要

首先,采用 t分布取代高斯分布来描述噪声,对信号的稀疏贝叶斯模型进行修正,减弱模型对脉冲噪声异常值的敏感性。然后,推导出一种多向量变分稀疏贝叶斯学习算法来求解修正模型,利用多个阵元的数据重构信号稀疏系数,提高了重构精度、改善了方法的跟踪性能。最后,设计试验对跟踪方法的性能进行仿真验证。试验结果表明,该方法在脉冲噪声下具有良好的稳健性和精确性。

关键词: 信息处理技术; 跳频信号跟踪; 脉冲噪声; t分布; 变分贝叶斯学习

中图分类号:TN911.72 文献标志码:A 文章编号:1671-5497(2015)06-2056-06

Robust tracking method for multiple frequency-hopping signals

SHANG Jia-dong, WANG Zu-lin, ZHOU Li-na, YANG Lan

School of Electronic and Information Engineering, Beihang University, Beijing 100191, China

Abstract

A robust tracking method for multiple frequency-hopping signals is presented. First, the measurement noise is modeled using the t distribution. Then, a novel Bayesian probability model is proposed to describe the multiple Frequency-Hopping (FH) signals tracking problem, such that the influence of the impulsive noise on the tracking performance can be attenuated efficiently. Finally, a Multiple Variational Sparse Bayesian Learning (M-VSBL) algorithm is derived for the proposed Bayesian model to estimate the hopping frequencies, directions of arrival and detect the hopping times. Simulation results demonstrate the robustness and accuracy of the proposed method under impulsive noise.

Keyword: information processing; frequency-hopping signals tracking; impulsive noise; t distribution; variational Bayesian learning

Show Figures

跳频(Frequency hopping, FH)通信的强抗干扰、抗截获性使其在通信领域的应用越来越广泛^[1], 对FH信号的截获、跟踪以及特征估计成为非合作通信和认知无线电领域中的重要研究内容^[2]。

目前已经出现诸多FH信号参数估计方法, 但能够实时跟踪FH信号的方法较少, 尤其针对多个FH信号。现有研究中仅出现了两类多FH信号跟踪方法:一类是基于时域自回归滑动平均(Autoregressive moving average, ARMA)模型方法^[3]以及采用粒子滤波算法(Particle filter, PF)改进的PF-ARMA模型方法^[4]; 另一类是基于多观测稀疏贝叶斯学习(Multiple sparse bayesian learning, M-SBL)的方法^[5]。ARMA模型方法对每个时刻的数据建立ARMA模型, 采用最小二乘法来最小化模型残差(噪声引起的残差)的l₂范数以求解模型, 并根据模型参数实时估计信号频率, 该方法计算简单, 但噪声适应性较差; PF-ARMA方法则通过引入PF算法提高了模型的噪声适应能力。M-SBL方法利用FH信号的时频稀疏特性, 建立基于高斯分布的稀疏模型来实时估计信号频率, 属于稀疏信号重构的问题, 该方法具有所需样本少、精度高的优点, 但计算复杂度高。

现有的FH信号跟踪方法都假设噪声服从高斯分布, 但实际环境中接收机会受大气噪声、海杂波以及无线信道噪声等的影响, 观测值中存在大量异常值, 噪声分布不再服从高斯形式^[6]。异常值的出现会破坏ARMA模型中l₂范数的有限性, 模型参数计算结果错误, 导致频率跟踪出现偏差^[7]; 并且PF算法的重采样结果会偏离真实的信号模型, 同样引起跟踪结果的偏差。M-SBL算法对由脉冲噪声非高斯分布引起的稀疏模型失配比较敏感, 稀疏向量的重构精度会下降^[8], 从而导致频率跟踪结果出现错误。因此, 现有的FH信号跟踪方法在脉冲噪声下均无法正常工作。

针对此问题, 本文利用t分布建立一种适合于脉冲噪声环境的新的多FH信号稀疏表示模型, 并采用变分贝叶斯学习(Variational sparse bayesian learning, VSBL)算法对模型求解, 来估计跳频信号的频率、到达角(Direction of arrival, DOA)和检测跳变时刻, 实现脉冲噪声下对FH信号的实时跟踪。

1 信号模型

1.1 阵列信号的稀疏贝叶斯模型

采用阵元间距为D的M元均匀线阵, 假设K个FH信号被天线截获, 信号的入射角、频率和复包络分别为 $\begin{matrix} {\{θ_{k}\}}_{k = 1}^{K} \end{matrix}$ 、 $\begin{matrix} {\{f_{k}\}}_{k = 1}^{K} \end{matrix}$ 和ρ _k, 在观测时间内保持不变, 系统采样间隔为T_s。定义变量φ _k=2π f_kT_s, ϕ _k=2π f_kDcosθ _k/C, 得到t时刻阵元m的观测值为:

$\begin{matrix} \begin{matrix} y_{m} (t) = \overset{K}{\sum_{k = 1}} ρ_{k} e^{j [(m - 1) ϕ_{k} + (t - 1) φ]} + e_{m} (t) = \\ \overset{K}{\sum_{k = 1}} x'_{k} e^{j (t - 1) φ_{k}} + e_{m} (t), 1 \leq t \leq N (1) \end{matrix} \end{matrix}$

式中:x'_k=ρ _k $\begin{matrix} e^{j (m - 1) ϕ_{k}} \end{matrix}$ ; e_m(t)为噪声。

构造冗余频率集φ '={φ '₁, …, φ '_P}, 满足 $\begin{matrix} {\{φ_{k}\}}_{k = 1}^{K} \end{matrix}$ ⊂φ '。阵列观测信号的稀疏模型可表示为如下的向量形式:

$\begin{matrix} Y = WX + E (2) \end{matrix}$

式中:Y=[y₁, …, y_M]∈ ℂ^{N× M}为观测矩阵, 其列向量y_m∈ ℂ^N对应阵元m; W=[w₁, …, w_P]∈ ℂ^{N× P}表示测量矩阵, 其中列向量w_p= $\begin{matrix} [e^{jφ'_{p}}, \dots, e^{j (N - 1) φ'_{p}}]^{T} \end{matrix}$ ; E为噪声矩阵; X=[x₁, …, x_M]∈ ℂ^{P× M}为稀疏信号矩阵, 其非零行位置对应了φ _k在φ '中的位置^[5], 通过重构矩阵X可以估计出FH信号的频率。

假设噪声服从高斯分布, 则式(2)可写成如下形式^[9]:

$\begin{matrix} \{\begin{matrix} p (Y | X) = \overset{M}{\prod_{m = 1}} {(π σ^{2})}^{- N / 2} \exp (- ‖ y_{m} - \\ W x_{m} ‖_{2}^{2} / σ^{2}) \\ p (X | α) = \overset{P}{\prod_{p = 1}} N (x_{p, \cdot} | 0, α_{p}^{- 1}) \end{matrix} (3) \end{matrix}$

式中:σ ²为噪声方差; x_p_{, ·}=[x_p_{, 1}, …, x_p_,_M]为矩阵X的第p行; α =[α ₁, …, α _P]为描述X的超参数, 服从伽马分布p(α _p)=Gam(α _p|a_p, b_p)。当α _p=0时, 对应的行向量x_p_{, ·}=0。

式(3)实质上为信号的稀疏贝叶斯表示模型, M-SBL算法通过最大化模型的边缘函数p(Y|α ), 可以估计出超参数α 的值^[9], 得到信号的频率。其中, 模型(3)的边缘函数为:

$\begin{matrix} \begin{matrix} p (Y | α) = \int p (Y | X) p (X | α) dX = \\ {|π Σ_{Y}|}^{- N / 2} \exp \{- tr (Y Σ_{Y} Y^{H})\} (4) \end{matrix} \end{matrix}$

式中:Σ _Y=σ ²I+WΛ ^-¹W^H, Λ =diag(α ^-¹)。

1.2 基于t分布的修正模型

由于脉冲噪声中存在大量异常值, E的概率密度分布出现重拖尾特性, 似然函数p(Y|X)不再服从高斯形式, 基于M-SBL的FH信号跟踪方法的性能因噪声模型的失配而急剧下降。与高斯分布相比, t分布具有更强的拖尾特性, 适合对重拖尾分布的噪声进行建模^[10]。本文采用t分布描述噪声, 对信号模型进行修正, 则模型的似然函数重写为:

$\begin{matrix} \begin{matrix} p (X | α) = Std (Y | WX, σ^{2}, v) \propto \\ {(1 + \frac{‖ Y - WX ‖_{F}^{2}}{v σ^{2}})}^{- \frac{v + 1}{2}} (5) \end{matrix} \end{matrix}$

式中:Std(· )表示t分布; v为分布的自由度参数, 反映了分布拖尾特性的显著程度, 当v趋于无穷时, 式(5)退化为式(3)的高斯形式。

2 稳健的多FH信号跟踪方法

利用M-SBL算法求解FH信号稀疏贝叶斯模型, 能够快速重构稀疏矩阵X, 估计信号的频率; 根据估计值的变化, 又可实时检测信号的跳变^[5]。但是, t分布的引入使得式(4)的计算困难, 导致用M-SBL算法无法得到α 的解析解。变分贝叶斯学习是近年来被提出的一种机器学习方法, 基于变分近似的思想, 能够以较少的计算量对复杂模型进行求解, 已逐步被应用到稀疏重构中。本文考虑采用变分贝叶斯学习算法来求解修正模型。

2.1 变分贝叶斯学习

VSBL算法根据向量x的先验, 选取一簇易处理的分布q(x, α )=q(x)q(α )去逼近真实的后验分布p(x, α |y), 并引入下界函数L(q(x, α ))来衡量近似程度^[11]:

$\begin{matrix} L (q (x, α)) = \iint q (x, α) \ln \{\frac{p (y, x, α)}{q (y, α)}\} dxdα (6) \end{matrix}$

根据变分泛函理论, 将式(6)分别对q(x)和q(α )求偏导, 得到q(x)与q(α )的通解表达式为:

$\begin{matrix} \{\begin{matrix} q (x) \propto \exp (E_{α} [lnp (y, x, α)]) \\ q (α) \propto \exp (E_{x} [lnp (y, x, α)]) \end{matrix} (7) \end{matrix}$

式中:p(y, x, α )表示y、x和α 联合概率分布。

对式(7)进行循环迭代, 更新q(x)和q(α )的参数, 可以使q(x, α )逐步逼近p(x, α |y), 当下界函数达到最大时, 停止迭代, 此时q(x)≈ p(x), 可以得到x估计值 $\begin{matrix} \hat{x} \end{matrix}$ =< x> =E_q₍_x₎(x)。

VSBL算法避开了对式(4)的计算, 从而克服了SBL算法超参数不可解的问题。为了适应式(2)的多向量形式, 将VSBL算法向多维进行扩展, 推导出一种多向量变分贝叶斯学习(Multiple VSBL, M-VSBL)算法。

2.2 M-VSBL算法

t分布可表示为无限个零均值高斯分布的线性组合^[10], 式(5)可以重写为:

$\begin{matrix} p (Y | X) = \overset{M}{\prod_{m = 1}} \int p (y_{m} | x_{m}, β) p (β) dβ (8) \end{matrix}$

式中:p(y_m|x_m, β )= $\begin{matrix} \prod_{n}^{=} \end{matrix}$ N(y_m_,_n|w_nx_m, $\begin{matrix} β_{n}^{- 1} \end{matrix}$ ); β 为隐变量, 服从伽马分布p(β )= $\begin{matrix} \prod_{n}^{=} \end{matrix}$ Gam(β _n|c_n, d_n), c_n=v/2, d_n=vσ ²/2。

根据式(3)和式(8), 观测矩阵Y, 稀疏矩阵X, 超参数α 和隐变量β 的联合概率分布表示为:

$\begin{matrix} p (Y, X, α, β) = p (Y | X, β) p (X | α) p (α) p (β) (9) \end{matrix}$

将式(9)代入式(7)中, 即得到X, α 与β 的近似分布q(X)、q(α )和q(β )。

首先, 计算q(X)。由于p(α )与p(β )不包含X项, 因此在计算时可将< α > 和< β > 按常数项处理。

$\begin{matrix} \begin{matrix} lnq (X) \propto \frac{1}{2} {\overset{M}{\sum_{m = 1}} \overset{N}{\sum_{n = 1}} [- \ln 2 π + < \ln β_{n} > - \\ < β_{n} > (y_{mn} - w_{n} {x_{m}}^{2}] + \overset{M}{\sum_{m = 1}} \overset{P}{\sum_{p = 1}} [- \ln 2 π + < \ln α_{p} > + \\ < α_{p} > x_{mp}^{2}]} + C = \\ - \frac{1}{2} \overset{M}{\sum_{m = 1}} [{(y_{m} - W x_{m})}^{T} B (y_{m} - W x_{m}) + \\ {x^{T}}_{m} A x_{m}] + C_{1} = - \overset{M}{\sum_{m = 1}} [\frac{{x^{T}}_{m} (W^{T} BW + A) x_{m}}{2} - \\ {x^{T}}_{m} (W^{T} B y_{m})] + C_{1} (10) \end{matrix} \end{matrix}$

式中:A=diag $\begin{matrix} (< α >) \end{matrix}$ ; B=diag $\begin{matrix} (< β >) \end{matrix}$ 。

由式(10)可知, X服从高斯分布:

$\begin{matrix} q (X) = \overset{M}{\prod_{m = 1}} N (x_{m} | μ_{m}, Σ) (11) \end{matrix}$

式中:μ _m和Σ 分别为:

$\begin{matrix} μ_{m} = ΣWB x_{m}; Σ = {(W^{T} BW + A)}^{- 1} (12) \end{matrix}$

同理, 计算q(α )的对数表达式:

$\begin{matrix} \begin{matrix} lnq (α) \propto \\ \overset{P}{\sum_{p = 1}} [(a_{p} - 1) \ln α_{p} + b_{p} α_{p}] + \\ \frac{1}{2} \overset{M}{\sum_{m = 1}} \overset{P}{\sum_{p = 1}} [\ln α_{p} + α_{p} < x_{pm}^{2} >] + C_{2} = \\ \overset{P}{\sum_{p = 1}} [(a_{p} + \frac{M}{2} - 1) \ln α_{p} + \\ (b_{p} + \frac{1}{2} \overset{M}{\sum_{m = 1}} < x_{pm}^{2} >) α_{p}] + C_{2} (13) \end{matrix} \end{matrix}$

由此可知, q(α )= $\begin{matrix} \prod_{p}^{=} \end{matrix}$ Gam(α _p| $\begin{matrix} {\hat{a}}_{p} \end{matrix}$ , $\begin{matrix} {\hat{b}}_{p} \end{matrix}$ ), 满足:

$\begin{matrix} {\hat{a}}_{p} = a + \frac{M}{2}; {\hat{b}}_{p} = b + \frac{1}{2} \overset{M}{\sum_{m = 1}} < x_{pm}^{2} > (14) \end{matrix}$

与q(α )的推导类似, 得到q(β )的表达式:

$\begin{matrix} q (β) = \overset{N}{\prod_{n = 1}} Gam (β_{n} | {\hat{c}}_{n}, {\hat{d}}_{n}) (15) \end{matrix}$

式中:参数 $\begin{matrix} {\hat{c}}_{n} \end{matrix}$ 和 $\begin{matrix} {\hat{d}}_{n} \end{matrix}$ 满足:

$\begin{matrix} \begin{matrix} {\hat{c}}_{n} = c + M / 2 (16) \\ {\hat{d}}_{n} = d_{n} + \frac{1}{2} < (y_{n} - w_{n} X) {(y_{n} - w_{n} X)}^{T} > (17) \end{matrix} \end{matrix}$

根据高斯分布和伽马分布的期望特性, 得到式(12)(14)(17)中各期望的计算结果:

$\begin{matrix} \begin{matrix} < x_{m} > = μ_{m}, < x_{m} {x^{T}}_{m} > = Σ + {μ^{T}}_{m} μ_{m} (18) \\ < α_{P} > = {\hat{a}}_{p} / {\hat{b}}_{p}, < β_{n} > = {\hat{c}}_{n} / {\hat{d}}_{n} (19) \end{matrix} \end{matrix}$

通过迭代计算式(12)(14)、(16)~(18), 直至下界函数L(q(X, α , β ))最大, 得到稀疏矩阵的估计结果 $\begin{matrix} \hat{X} \end{matrix}$ = $\begin{matrix} [{\hat{μ}}_{1}, \dots, {\hat{μ}}_{M}]^{T} \end{matrix}$ 。其中, $\begin{matrix} {\hat{μ}}_{m} \end{matrix}$ 为μ _m的最终迭代值。

2.3 频率估计、调试检测以及DOA估计

由矩阵 $\begin{matrix} \hat{X} \end{matrix}$ 的非零行位置 $\begin{matrix} {\{p_{k}\}}_{k = 1}^{K} \end{matrix}$ , 估计本驻留时间内各信号的频率:

$\begin{matrix} {\hat{f}}_{k} = \frac{p_{k}}{P} f_{s}, k = 1, \dots, K (20) \end{matrix}$

同时, 得到阵列N+1时刻的预测值:

$\begin{matrix} {\hat{y}}_{N + 1} = [e^{j φ_{1} (N + 1)}, \dots, e^{j φ_{P} (N + 1)}] \cdot \hat{X} (21) \end{matrix}$

利用阵列数据的预测误差, 可判断是否发生频率跳变^[3]。考虑到脉冲噪声的异常值对l₂范数的有限性破坏, 本文选择Huber惩罚函数作为判断频率跳变的代价函数, 减小异常值的影响^[8]。基于Huber函数的频率跳变判决公式为:

$\begin{matrix} \overset{M}{\sum_{m = 1}} ρ_{α} (y_{m, t_{H}} - {\hat{y}}_{m, t_{H}}) \overset{H_{0}}{\underset{H_{1}}{≷}} ξ (22) \end{matrix}$

式中:H₁表示“ 发生跳变” ; H₀表示“ 未发生跳变” ; ξ 为判决门限, 由t_h之前样本点的预测误差得到:

$\begin{matrix} ξ = μ (\frac{1}{t_{h} - N - 1} \overset{t_{h} - 1}{\sum_{t = N + 1}} \overset{M}{\sum_{m = 1}} ρ_{α} (y_{m, t} - {\hat{y}}_{m, t})) (23) \end{matrix}$

Huber惩罚函数ρ _α(· )的定义为:

$\begin{matrix} ρ_{α} (u) = \{\begin{matrix} u^{2}, \\ 2 α | u |- α^{2}, \end{matrix} \begin{matrix} | u |\leq α \\ | u |> α \end{matrix} (24) \end{matrix}$

式中:α =λ $\begin{matrix} {\hat{σ}}^{2} \end{matrix}$ 为Huber函数的惩罚阈值; $\begin{matrix} {\hat{σ}}^{2} \end{matrix}$ 为方差估计值 $\begin{matrix} {\hat{σ}}^{2} \end{matrix}$ = $\begin{matrix} {\hat{d}}_{n} \end{matrix}$ / $\begin{matrix} {\hat{c}}_{n} \end{matrix}$ ; μ 、λ 为权重因子, 一般μ 取3~5, λ 取2~3^[12]。

针对同步跳频网络的信号分选还需要信号的方位角信息^[4]。取 $\begin{matrix} \hat{X} \end{matrix}$ 所有的非零行组成矩阵 $\begin{matrix} \tilde{X} \end{matrix}$ = $\begin{matrix} [x_{p_{1}, \cdot}, \dots, x_{p_{K}, \cdot}]^{T} \end{matrix}$ , 计算ϕ _k的估计值 $\begin{matrix} {\hat{ϕ}}_{k} \end{matrix}$ :

$\begin{matrix} {\hat{ϕ}}_{k} = \frac{1}{M - 1} \overset{M}{\sum_{m = 2}} angle ({\tilde{x}}_{m, k + 1} / {\tilde{x}}_{m, k}), k = 1, \dots, K (25) \end{matrix}$

式中:angle $\begin{matrix} (\cdot) \end{matrix}$ 表示计算复数向量的夹角; $\begin{matrix} {\tilde{x}}_{m, k} \end{matrix}$ 为矩阵 $\begin{matrix} \tilde{X} \end{matrix}$ 的m行k列的元素。

由式(25)可以得到DOA的估计值:

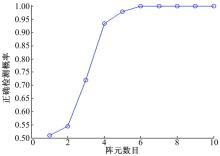
$\begin{matrix} {\hat{θ}}_{k} = \arccos ({\hat{ϕ}}_{k} / (2 π {\hat{f}}_{k} d) \times C), k = 1, \dots, K (26) \end{matrix}$

3 试验结果和分析

通过仿真来验证本文方法的性能。由于ARMA模型方法的噪声适应性较差, 因此仅选取PF-ARMA方法和M-VSBL方法与本文方法进行对比。此外还分析了阵元数目与跳时检测概率的关系, 验证了多观测向量对方法跟踪性能的改善程度。

仿真条件:阵元间隔为半波长的6元线性阵列, 2个入射角分别为80° 和60° 的跳频信号。工作频段0~20 MHz, 采样频率50 MHz, 频率集数目为P=64, 数据长度N=6。采用2元混合高斯模型模拟脉冲噪声^[8], 背景噪声方差 $\begin{matrix} σ_{g}^{2} \end{matrix}$ =0.005, 冲击方差 $\begin{matrix} σ_{k}^{2} \end{matrix}$ =k $\begin{matrix} σ_{g}^{2} \end{matrix}$ 。k为方差比, 其值越大噪声的脉冲特性越强; k=1时为高斯噪声, 冲击值的出现概率为0.1。

3.1 频率实时跟踪结果

首先对频率跟踪性能进行仿真验证。假设2个异步跳频信号, 信号1频率为10、14、4 MHz, 分别持续30、60、60个样本点, 信号2频率为8、16、7 MHz, 持续60、60、30个样本点, 方差比取k=200。图1(b)(c)(d)给出了3种方法的频率跟踪结果, 实线表示频率的真实值, 图1(a)则为噪声的时域波形。

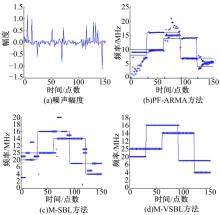	Figure Option View Download New Window
	图1 脉冲噪声及信号频率的实时跟踪结果Fig.1 Impulsive noise and the real-time frequency tracking results of multiple FH signal

通过对比发现, 由于PF-ARMA与M-SBL方法对脉冲噪声稳健性较差, 频率估计结果在冲击点附近出现偏差, 偏差值最大可达8 MHz; 而基于修正模型的M-VSBL方法没有出现频率偏差点, 具有较高的频率估计精度。

3.2 跳变时刻的正确检测概率

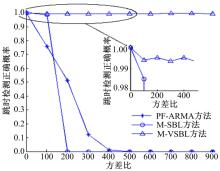
采用正确检测概率来衡量方法的跳时检测性能^[3]。k从1到1000变化, 在0~20 MHz内随机选取信号频率, 随机产生40个数据点, 并在第15点处改变信号1的频率。若跳时检测结果为第15或16点, 则认为检测正确。图2给出了不同k值下进行1000次蒙特卡洛仿真得到的跳时检测正确概率。

	Figure Option View Download New Window
	图2 跳时正确检测概率随方差比的变化曲线Fig.2 Hopping time detecting probability for different k

由图2可以看出, PF-ARMA与M-SBL方法对脉冲噪声的异常值非常敏感, 检测概率随k值的增大而急剧下降, 在k≥ 200时M-SBL的检测概率就已经接近于0。M-VSBL方法则表现出较好的稳健性, 所有k值下的检测概率均在1左右。该试验结果表明M-VSBL方法具有较好的稳健性, 对脉冲噪声具有较好的鲁棒性。

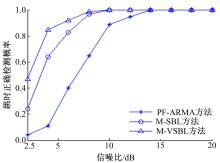
进一步对3种方法在高斯噪声下的跳时正确检测概率进行仿真和对比, 以分析信噪比对方法性能的影响。方差比k为1, 信噪比SNR=-20log(σ _g)在2~20 dB内变化。图3给出了跳时检测正确概率随信噪比变化的曲线。

	Figure Option View Download New Window
	图3 跳时正确检测概率随信噪比的变化曲线Fig.3 Hopping time detecting probability for different values of SNR

由图3可以看出:在高斯噪声下M-VSBL方法的信噪比适应能力优于其他两种方法; 100%正确检测所需的最小信噪比为6 dB, 分别比PF-ARMA和M-SBL方法低8 dB和2 dB。该仿真结果表明M-VSBL方法同样适用于高斯噪声环境; 并且通过提高信噪比能够有效改善方法的跟踪性能。

3.3 DOA的估计结果

在1~1000内调整方差比k, 其他参数保持与3.1节相同, 仿真对比M-VSBL与PF-ARMA方法的DOA估计性能(M-SBL方法无法估计DOA)。不同方差比下两种方法下的DOA估计结果如表1所示。

表1 跳频信号的DOA估计结果 Table 1 DOA estimations of FH signals

通过与真实值对比, PF-ARMA方法的DOA估计误差范围为0.03° ~70° , 其值随k的增大而逐渐增加; 在k≥ 200时, 估计误差已超过10° , 已无法用于同步跳频信号的分选, k≥ 400时因频率偏差过大, DOA估计结果无意义。而M-VSBL方法的估计误差在0~0.22° 范围内, 并且k在1~1000范围内, 其值变化不会影响DOA估计精度。

3.4 阵元数目与频率跟踪精度的关系

设置方差比k=200, 阵元数目为1~10, 采用3.2节的信号与脉冲噪声参数, 得到跳时检测概率与阵元数目之间的关系曲线如图4所示。

	Figure Option View Download New Window
	图4 跳时检测概率与阵元数目的关系曲线Fig.4 Hopping time detecting probability for different array size M

由图4可以看出:随着阵元数目M的增加, 跳时检测概率逐渐增大, M≥ 6时达到1。即在该噪声条件下, 采用6元天线就能实现对信号的精确跟踪。该试验结果验证了多个阵元对M-VSBL方法跟踪性能的改善, 同时为系统天线的设计提供参考。

4 结束语

提出了一种基于变分贝叶斯学习的多FH信号跟踪方法M-VSBL方法, 用于在脉冲噪声环境下对多个FH信号的频率跟踪、跳变检测以及DOA估计。利用t分布对FH信号的稀疏表示模型进行修正, 提高了模型的稳健性。试验结果表明, 受噪声中异常值的影响, 现有的跟踪方法在脉冲噪声下将会崩溃, 而M-VSBL方法能够有效地消除异常值的影响, 实现对多个FH信号的精确跟踪; 而且, M-VSBL方法不仅对脉冲噪声具有鲁棒性, 其在高斯噪声下的跟踪性能也优于现有的方法。此外, 通过增加阵列中的阵元数目, 还能够进一步改善其跟踪性能。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Glisic S, Nikolic Z, Milosevic N, et al. Advanced frequency hopping modulation for spread spectrum WLAN[J]. IEEE Journal on Selected Areas in Communications, 2000, 18(1): 16-29. [本文引用:1]
[2]	Liu X, Sidiropoulos N D, Swami A. Blind high-resolution localization and tracking of multiple frequency hopped signals[J]. IEEE Transaction on Signal Processing, 2002, 50(4): 889-900. [本文引用:1]
[3]	Liu Zhang-meng, Huang Zhi-tao, Zhou Yi-yu. Hopping instants detection and frequency tracking of FH signals with single or multiple channels[J]. IET Communications, 2012, 6(1): 84-89. [本文引用:3]
[4]	Sha Zhi-chao, Liu Zhang-meng, Huang Zhi-tao. Online hop timing detection and frequency estimation of multiple FH signals[J]. ETRI Journal, 2013, 35(5): 748-756. [本文引用:2]
[5]	王丰华, 沙志超, 刘章孟, 等. 基于贝叶斯稀疏学习的多跳频信号频率跟踪方法[J]. 电子与信息学报, 2013, 35(6): 1395-1399. Wang Feng-hua, Sha Zhi-chao, Liu Zhang-meng, et al. A frequency tracking method for multiple frequency-hopping signals based on sparse Bayesian learning[J]. Journal of Electronic & Information Technology, 2013, 35(6): 1395-1399. [本文引用:3]
[6]	Zimmermann M, Dostert K. Analysis and modeling of impulsive noise in broad-band powerline communications[J]. IEEE Transactions on Electromagnetic Compatibility, 2002, 44(1): 249-258. [本文引用:1]
[7]	Maronna R A, Martin R D, Yohai V J. Robust statistics: theory and methods[M]. New York: John Wiely & Sons, 2006. [本文引用:1]
[8]	Pham D S, Venkatesh S. Improved image recovery from compressed data contaminated with impulsive noise[J]. IEEE Transactions on Image Processing, 2012, 21(1): 397-405. [本文引用:3]
[9]	Wipf D P, Rao B D. An empirical Bayesian strategy for solving the simultaneous sparse approximation problem[J]. IEEE Transactions on Signal Processing, 2007, 55(7): 3704-3716. [本文引用:2]
[10]	Lange K L, Little R J A, Taylorb J M G. Robust statistical modeling using the t distribution[J]. Journal of the American Statistical Association, 1989, 84(408): 881-896. [本文引用:2]
[11]	Bishop C M, Tipping M E. Variational relevance vector machines[C]∥Proceedings of the Sixteenth Conference on Uncertainty in Artificial Intelligence, Menlo Park, CA, USA, 2000: 46-53. [本文引用:1]
[12]	陈坤, 田华, 何晶, 等. 一种基于Huber函数的康塔方位稳健估计算法[J]. 空军工程大学学报: 自然科学版, 2013, 14(6): 18-22. Chen Kun, Tian Hua, He Jing, et al. A robust estimation algorithm of TACAN azimuth based on Huber function[J]. Journal of Air Force Engineering University(Natural Science Edition), 2013, 14(6): 18-22. [本文引用:1]

2000

0.0

... 跳频(Frequency hopping,FH)通信的强抗干扰、抗截获性使其在通信领域的应用越来越广泛^[1],对FH信号的截获、跟踪以及特征估计成为非合作通信和认知无线电领域中的重要研究内容^[2] ...

2002

0.0

2012

0.0

... 现有研究中仅出现了两类多FH信号跟踪方法:一类是基于时域自回归滑动平均(Autoregressive moving average,ARMA)模型方法^[3]以及采用粒子滤波算法(Particle filter,PF)改进的PF-ARMA模型方法^[4] ...

... 利用阵列数据的预测误差,可判断是否发生频率跳变^[3] ...

... 2 跳变时刻的正确检测概率采用正确检测概率来衡量方法的跳时检测性能^[3] ...

2013

0.0

... 针对同步跳频网络的信号分选还需要信号的方位角信息^[4] ...

2013

0.0

. 2013, 35(6):1395-1399 DOI:doi:10.3724/SP.J.1146.2012.01493

A frequency tracking method for multiple frequency-hopping signals based on sparse Bayesian learning

基于贝叶斯稀疏学习的多跳频信号频率跟踪方法

Wang Feng-hua , Sha Zhi-chao , Liu Zhang-meng

王丰华, 沙志超, 刘章孟

Most of previous blind parameter estimation methods of Frequency Hopping (FH) signals with a single channel do not adapt to overlapped signals. Moreover, the single- and multiple-channel-based methods use batch processing techniques almost, so they are not able to estimate FH signals in real time. To get real-time tracking reliably, a novel method for single- and multiple-channel-based frequency estimating and hop timing detecting for FH signals is proposed to track the frequency of multiple frequency-hopping signals based on Sparse Bayesian Learning (SBL). Firstly, overlapped FH signals sparse representation model is established. Then, the Sparse Bayesian Learning is used to estimate hopping frequencies and detect the frequency hops once they happen. Numerical examples are carried out to demonstrate the effectiveness of the proposed method.

以往的跳频信号参数盲估计方法大多难以适应多个信号同时存在的情况，且需要积累一定数量的样本以后才能从中提取所需要的信息。为了稳定实时地跟踪跳频信号的频率，该文提出一种利用贝叶斯稀疏学习的单/多通道跳频信号频率估计和跳变时刻检测方法来实现多跳频信号频率的实时跟踪。首先建立了多跳频信号的稀疏表示模型，然后介绍了多观测贝叶斯稀疏学习算法及跳变时刻实时检测方法，最后仿真结果验证方法的有效性。

... 另一类是基于多观测稀疏贝叶斯学习(Multiple sparse bayesian learning,M-SBL)的方法^[5] ...

... '中的位置^[5],通过重构矩阵X可以估计出FH信号的频率 ...

... 根据估计值的变化,又可实时检测信号的跳变^[5] ...

2002

0.0

... 现有的FH信号跟踪方法都假设噪声服从高斯分布,但实际环境中接收机会受大气噪声、海杂波以及无线信道噪声等的影响,观测值中存在大量异常值,噪声分布不再服从高斯形式^[6] ...

2006

0.0

... 异常值的出现会破坏ARMA模型中l₂范数的有限性,模型参数计算结果错误,导致频率跟踪出现偏差^[7] ...

2012

0.0

... M-SBL算法对由脉冲噪声非高斯分布引起的稀疏模型失配比较敏感,稀疏向量的重构精度会下降^[8],从而导致频率跟踪结果出现错误 ...

... 考虑到脉冲噪声的异常值对l₂范数的有限性破坏,本文选择Huber惩罚函数作为判断频率跳变的代价函数,减小异常值的影响^[8] ...

... 采用2元混合高斯模型模拟脉冲噪声^[8],背景噪声方差 σg2=0 ...

2007

0.0

... 假设噪声服从高斯分布,则式(2)可写成如下形式^[9]: ...

... 的值^[9],得到信号的频率 ...

1989

0.0

... 与高斯分布相比,t分布具有更强的拖尾特性,适合对重拖尾分布的噪声进行建模^[10] ...

... 2 M-VSBL算法t分布可表示为无限个零均值高斯分布的线性组合^[10],式(5)可以重写为: ...

2000

0.0

... ))来衡量近似程度^[11]: ...

2013

0.0

. 2013, 14(6):18-22 DOI:doi:10.3969/j.issn.1009-3516.2013.06.005

A robust estimation algorithm of TACAN azimuth based on Huber function

一种基于Huber函数的康塔方位稳健估计算法

Chen Kun , Tian Hua , He Jing

陈坤, 田华, 何晶

为抑制峰值检测器提取的塔康峰值包络中野值的影响，提出了一种方位稳健估计算法。利用基于最大似然准则的 Huber 函数压缩大于门限的误差，减小野值在算法中的权重。并采用双重门限对 Huber 函数作了改进，消除较大野值的权重，对较小的野值进行压缩，给出了门限参数的选取依据。该方法不需要噪声的先验统计知识，能有效抑制野值的影响。仿真结果表明：所提算法的参数估计精度较传统的 Huber 估计器和最小二乘算法(Least Square)有明显提高，在3 dB 功率信噪比环境下，估计误差小于0.5°，满足塔康系统要求。

... 取2~3^[12] ...