基于最小均方误差的单载波系统低复杂度频域迭代均衡

引用本文

邹奇峰, 谭学治, 刘梅, 马琳. 基于最小均方误差的单载波系统低复杂度频域迭代均衡. 2015, 45(6): 2062-2068
ZOU Qi-feng, TAN Xue-zhi, LIU Mei, MA Lin. Low complexity frequency domain iterative equalization based on minimum mean square error for single carrier systems. Journal of Jilin University Engineering and Technology Edition, 2015, 45(6): 2062-2068 复制到剪切板

Permissions

基于最小均方误差的单载波系统低复杂度频域迭代均衡

邹奇峰, 谭学治, 刘梅, 马琳

哈尔滨工业大学电子与信息工程学院,哈尔滨 150080

谭学治(1958-),男,教授,博士生导师.研究方向:专用移动通信系统,个人移动通信,通信新技术,智能信息系统,认知无线电技术.E-mail:tanxz1957@hit.edu.cn

作者简介:邹奇峰(1981-),男,博士研究生.研究方向:宽带单载波通信系统信道估计与均衡.E-mail:zouqifeng163@163.com

基金:国家自然科学基金项目(61571162,61101122); 国家科技重大专项项目(2014ZX03004003,2011ZX03004004); 公安部科技专项项目(2015GABJC38,2015GABJC37)

摘要

针对单载波频域均衡(SC-FDE)系统中迭代块判决反馈均衡(IBDFE)算法随迭代次数增加运算复杂度迅速提高的问题,提出了一种低复杂度频域迭代均衡算法。利用均方误差(MSE)准则对检测点误差信号进行分析,对确定的信道增益每次迭代的滤波器系数为定值,并通过在帧结构插入特殊字序列UW作为循环前缀来减小系统开销。理论分析和仿真实验结果表明:本文算法在较高信噪比下比传统的线性均衡性能更好,而在相同迭代次数时接近IBDFE算法性能且比IBDFE算法复杂度大大降低。

关键词: 通信技术; 单载波频域均衡; 判决反馈均衡; 均方误差准则; 特殊字序列

中图分类号:TN929 文献标志码:A 文章编号:1671-5497(2015)06-2062-07

Low complexity frequency domain iterative equalization based on minimum mean square error for single carrier systems

ZOU Qi-feng, TAN Xue-zhi, LIU Mei, MA Lin

School of Electronics and Information Engineering, Harbin Institute of Technology, Harbin 150080,China

Abstract

In Single Carrier Frequency Domain Equalization (SC-FDE) system, a novel equalization algorithm based on Mean Square Error (MSE) criterion was proposed in order to predigest the complexity of Iterative Block Decision Feedback Equalization (IBDFE). The coefficients of the filter can be kept unchanged in each iteration based on the given channel frequency response. The Unique Word (UW) sequence, which was inserted into frame structure and the cyclic prefix, could reduce the overhead of the system. The simulation results show that the performance of the proposed algorithm is better than the conventional linear equalization algorithm in high Signal to Noise Ratio (SNR) and close to the IBDFE algorithm in the same iteration times. However, the complexity of the proposed algorithm is lower than that of the conventional IBDFE algorithm.

Keyword: communication; single carrier frequency domain equalization(SC-FDE); decision feedback equalization; mean square error; unique word sequence

Show Figures

在宽带数据传输过程中如何对抗信道频率选择性衰落导致的码间干扰(ISI)始终是无线通信领域面对的基本挑战。1994年Sari和Karam等提出了单载波频域均衡(SC-FDE)技术, 并受到越来越多的关注^{[1, 2, 3]}。在未编码系统中单载波频域均衡与OFDM的性能类似^[4], 且SC-FDE具有更小的峰均比(PAPR)^[5], 对相位噪声的敏感性更低。频域均衡器的结构设计和相关信号处理算法是单载波系统的关键技术。传统的线性频域均衡器(FD-LE)结构简单、计算复杂度低, 但在频率选择性信道中由于噪声的传播均衡性能较差^[6]。Falconer等提出了时频混合判决反馈均衡算法HD-DFE^[7], HD-DFE由于加入反馈部分, 进一步消除了ISI, 因而性能强于FD-LE, 但由于反馈部分在时域需要进行大量矩阵运算, 滤波器系数复杂度和误差随反馈阶数指数增加。Benvenuto等提出了频域迭代块判决反馈均衡(FD-IBDFE)算法^[8], 该算法中均衡器前馈和反馈滤波部分均在频域实现, 通过FFT变换相对时频混合结构降低了运算复杂度, 且在多次迭代后性能较好, 但该算法每次迭代都要重新计算滤波系数, 并对多个参数进行估计, 在迭代次数增加后仍然具有较高复杂度。

本文给出一种低复杂度频域迭代判决反馈均衡(LC-IBDFE)算法, 采用特殊字序列UW做为循环前缀^[9], 并起到信道跟踪的作用, 单载波系统接收机不需要删除接收信号中的UW对应部分, 可以直接进行串/并转换和FFT进而减小了系统开销。通过对检测点信号的均方误差(MSE)进行分析并使其最小化, 每次迭代的滤波系数只取决于预设信噪比和信道冲击响应。通过对判决信号进行处理能够在相同的迭代次数下取得和FD-IBDFE算法近似的系统性能, 且算法复杂度比FD-IBDFE降低很多, 此外本文还依据判决误差功率设计了一种迭代停止准则。

1 传输结构和系统模型

宽带单载波系统发射机将要发射的数据流分为多个长度为M的数据块, 并且在每个发射数据块前插入一个特殊字UW序列{k_l $\begin{matrix} }_{l = 0}^{N - 1} \end{matrix}$ , UW序列为N个符号长度。发射符号总长度P=M+N可以表示为:

$\begin{matrix} \begin{matrix} s = {[s_{0}, s_{1}, \dots, s_{P - 1}]}^{T} = \\ {[d_{0}, d_{1}, \dots, d_{M - 1}, k_{0}, k_{1}, \dots, k_{N - 1}]}^{T} (1) \end{matrix} \end{matrix}$

在802.16a标准中单载波系统的特殊字UW序列既用作循环前缀又被当做训练序列用于信道估计。用作循环前缀时要求UW的长度必须大于信道最大时延长度, 为了确保信道的每一个频率成分被均匀探测, 要求用于信道估计的UW有较好的相关性和平稳的频率响应, 其进行频域均衡后所有的频率分量相等或者几乎相等。根据标准确定的帧结构如图1所示。

	Figure Option View Download New Window
	图1 采用UW的SC-FDE系统发送信号帧结构Fig.1 Frame structure of SC-FDE system with UW

采用循环复制技术插入CP的单载波或OFDM系统需要在接收机先去掉接收信号的循环前缀再进行FFT, 而插入特殊字的单载波系统接收机则不需要删除接收信号中的特殊字序列, 直接进行FFT, 因此系统开销要比采用CP的结构小。802.16a标准中给出两种UW序列构造方式, 分别采用Frank-Zadoff序列以及Chu序列生成, 它们都是恒幅值自相关(CAZAC)序列, 且都有良好的周期自相关特性。为了方便FFT运算, 序列长度一般设为2的幂次。标准中建议序列长度为64时, 必须选择Frank-Zadoff序列, 其他长度时可选Chu序列或Frank-Zadoff序列中的任意一种。为方便FFT运算本文也选用Frank-Zadoff序列作为特殊字, 其表达式为:

$\begin{matrix} \begin{matrix} θ_{frank} [n = a + b \sqrt{D}] = \frac{2 πab}{\sqrt{D}} (2) \\ a = 0, 1, \dots, \sqrt{D} - 1; b = 0, 1, \dots, \sqrt{D} - 1 \end{matrix} \end{matrix}$

包含均衡模块的SC-FDE系统简易框图如图2所示。

	Figure Option View Download New Window
	图2 SC-FDE仿真系统模型Fig.2 SC-FDE simulation system model

当第j块发射信号s(j)经过多径信道并经过FFT处理后得到的频域接收信号为:

$\begin{matrix} R_{p} (j) = H_{p} S_{p} (j) + W_{p} (j) (3) \end{matrix}$

式中:H_p为信道的频域响应; W_p为高斯白噪声的频域形式。

2 低复杂度频域迭代均衡算法

2.1 基于最小均方误差的均衡器设计

本文提出的LC-IBDFE采用与文献[8]近似的频域均衡器结构, 如图3所示。前馈和反馈滤波均在频域进行, 通过多次迭代来消除由于无线信道频率选择性衰落造成的幅度和相位影响, 并增强检测数据的可靠性。第i次迭代时域接收信号r_n经过串并转换和FFT变换后得到频域信号R_p, 与前馈滤波系数C_p频域相乘后得到符号Z_p, 通过对上一次迭代判决检测后得到的信号进行时频转换并重新插入UW得到检测符号 $\begin{matrix} {\hat{S}}_{p}^{i - 1} \end{matrix}$ , 将 $\begin{matrix} {\hat{S}}_{p}^{i - 1} \end{matrix}$ 与反馈滤波系数B_p频域相乘后再与Z_p频域叠加得到频域向量信号U_p, 经过IFFT处理并去除UW后变为时域信号, 再经过并串转换和判决检测得到本次迭代输出信号。文献[8]中每次迭代都需要对上一次迭代判决序列与发送序列的相关因子进行估计来重新计算滤波器的系数, 每次迭代得到不同的B_p和C_p才能继续迭代下去, 这样随迭代次数增加滤波器系数估计复杂度大大增加。为减少计算复杂度, 本文基于MSE准则对检测点误差信号进行分析。

	Figure Option View Download New Window
	图3 低复杂度频域迭代块判决反馈均衡器结构框图Fig.3 Proposed equalizer structure of LC-IBDFE

假设当反馈滤波进行第i-1次迭代时, $\begin{matrix} ε_{p}^{i - 1} \end{matrix}$ 表示传输符号S_p与检测符号 $\begin{matrix} {\hat{S}}_{p}^{i - 1} \end{matrix}$ 在第i-1次迭代的频域判决误差, 方差为 $\begin{matrix} σ_{ε (i - 1)}^{2} \end{matrix}$ , 检测的包含UW序列的数据表示为 $\begin{matrix} {\hat{s}}^{i - 1} \end{matrix}$ , 进行FFT变换后有:

$\begin{matrix} {\hat{S}}_{p}^{i - 1} = S_{p} + ε_{p}^{i - 1}, p = 0, 1, \dots, P - 1 (4) \end{matrix}$

则当第i次迭代时前馈滤波与反馈滤波在频域叠加后得到:

$\begin{matrix} U_{p}^{i} = C_{p}^{i} R_{p} + B_{p}^{i} (S_{p} + ε_{p}^{i - 1}) (5) \end{matrix}$

在第i次迭代, 由图3可得检测点的均方误差(MSE)为:

$\begin{matrix} \begin{matrix} MS E^{i} = E [{|{\tilde{d}}_{n}^{i} - d_{n}|}^{2}] = \\ \frac{1}{P} \overset{P - 1}{\sum_{n = 0}} E [{|u_{n}^{i} - s_{n}|}^{2}] = \\ \frac{1}{P^{2}} \overset{P - 1}{\sum_{p = 0}} E [{|U_{p}^{i} - S_{p}|}^{2}] (6) \end{matrix} \end{matrix}$

根据帕萨瓦尔定理, 由式(4)~(6)得到:

$\begin{matrix} \begin{matrix} MS E^{i} (C^{i}, B^{i}) = \\ \frac{1}{P^{2}} \overset{P - 1}{\sum_{p = 0}} E [{|C_{p}^{i} R_{p} + B_{p}^{i} (S_{p} + ε_{p}^{i - 1}) - S_{p}|}^{2}] = \\ \frac{1}{P^{2}} \overset{P - 1}{\sum_{p = 0}} \{{|C_{p}^{i} H_{p} + B_{p}^{i} - 1|}^{2} σ_{S}^{2} + {|C_{p}^{i}|}^{2} σ_{W}^{2} + \\ {|B_{p}^{i}|}^{2} σ_{ε (i - 1)}^{2} + 2 R [(C_{p}^{i} H_{p} + \\ B_{p}^{i} - 1) {(B_{p}^{i})}^{*} ξ^{i - 1}]\} (7) \end{matrix} \end{matrix}$

式中:R(x)为x的实部, ξ ^i-¹=E[S_p( $\begin{matrix} ε_{p}^{i - 1} \end{matrix}$ )^*]为发送信号与第i-1次迭代的频域判决误差信号的互相关函数。

优化目标是使均方误差MSE最小, 为反馈滤波去拖尾可以得到约束条件:

$\begin{matrix} \overset{P - 1}{\sum_{p = 0}} B_{p}^{i} = 0 (8) \end{matrix}$

设λ ⁱ为拉格朗日乘数, 根据拉格朗日乘数法定义目标函数为:

$\begin{matrix} \begin{matrix} f (C^{i}, B^{i}, λ^{i}) = \\ MS E^{i} (C^{i}, B^{i}) + λ^{i} \overset{P - 1}{\sum_{p = 0}} B_{p}^{i} (9) \end{matrix} \end{matrix}$

对于式(9)分别关于 $\begin{matrix} C_{p}^{i} \end{matrix}$ 、 $\begin{matrix} B_{p}^{i} \end{matrix}$ 以及λ ⁱ求偏导, 当导数值为零可得到滤波器的系数为:

$\begin{matrix} \begin{matrix} B_{p}^{i} = - \frac{σ_{S}^{2} + ξ^{i - 1}}{σ_{S}^{2} + 2 R [ξ^{i - 1}] + σ_{ε (i - 1)}^{2}} (C_{p}^{i} H_{p} - α^{i}) (10) \\ C_{p}^{i} = \frac{(σ_{S}^{2} - \frac{{|σ_{S}^{2} + ξ^{i - 1}|}^{2}}{σ_{S}^{2} + 2 R [ξ^{i - 1}] σ_{ε (i - 1)}^{2}} α^{i}) H_{p}^{*}}{σ_{W}^{2} + (σ_{S}^{2} - \frac{{|σ_{S}^{2} + ξ^{i - 1}|}^{2}}{σ_{S}^{2} + 2 R [ξ^{i - 1}] σ_{ε (i - 1)}^{2}}) {|H_{p}|}^{2}} (11) \\ 式中 : \\ α^{i} = σ_{S}^{2} β^{i} {(1 + \frac{{|σ_{S}^{2} + ξ^{i - 1}|}^{2}}{σ_{S}^{2} + 2 R [ξ^{i - 1}] + σ_{ε (i - 1)}^{2}} β^{i})}^{- 1} (12) \\ β^{i} = \frac{1}{P} \overset{P - 1}{\sum_{p = 0}} {|H_{p}|}^{2} [σ_{W}^{2} + \\ {(σ_{S}^{2} - \frac{{|σ_{S}^{2} + ξ^{i - 1}|}^{2}}{σ_{S}^{2} + 2 R [ξ^{i - 1}] + σ_{ε (i - 1)}^{2}})]}^{- 1} (13) \end{matrix} \end{matrix}$

由重新得到的前馈和反馈滤波器系数表达式可知:每次迭代需要估计噪声功率 $\begin{matrix} σ_{W}^{2} \end{matrix}$ =P $\begin{matrix} σ_{w}^{2} \end{matrix}$ 和 $\begin{matrix} σ_{ε (i - 1)}^{2} \end{matrix}$ 、ξ ^i-¹, $\begin{matrix} σ_{s}^{2} \end{matrix}$ 由符号星座映射得到, 视为已知量, 则发送信号的频域功率与时域功率之间的关系为:

$\begin{matrix} σ_{S}^{2} = E [\overset{P - 1}{\sum_{n_{1} = 0}} s_{n_{1}} e^{- j \frac{2 π}{P} n_{1} p} \overset{P - 1}{\sum_{n_{2} = 0}} s_{n_{2}}^{*} e^{j \frac{2 π}{P} n_{2} p}] = P σ_{s}^{2} (14) \end{matrix}$

以下考虑如何高效地估计 $\begin{matrix} σ_{ε (i - 1)}^{2} \end{matrix}$ 、ξ ^i-¹、 $\begin{matrix} σ_{W}^{2} \end{matrix}$ 或SNR。

2.2 参数估计

判决误差功率 $\begin{matrix} σ_{ε (i - 1)}^{2} \end{matrix}$ 由调制方式和误符号率(SER)决定, 若星座点映射方式为格雷编码, 则低信噪比情况下判决误差会使符号误判为相邻的符号, 即只有一个同相或正交的符号向量将会误判, 不同的QAM调制方案中 $\begin{matrix} σ_{ε (i - 1)}^{2} \end{matrix}$ 可以表示为:

$\begin{matrix} σ_{ε (i - 1)}^{2} = μ σ_{S}^{2} Ω_{s}^{i - 1} (15) \end{matrix}$

式中:对于4QAM、16QAM、64QAM, μ 的取值分别为2, 2/5, 2/21。 $\begin{matrix} Ω_{s}^{i - 1} \end{matrix}$ 表示第i-1次迭代的SER。

根据文献[7, 8], 判决反馈结构均衡器的误差传播发生在一个传输块(或发送信号帧)内, 并对一个传输块数据整体进行检测, 后一次迭代误差只取决于前一次迭代的可靠性。而作为训练序列的特殊字长度与帧长度计算和选择可以保证一个发送信号帧的传输时间内信道状态变化不大, 因此对于每个接收的信号帧可以假设在每次迭代过程中瞬时误符号率 $\begin{matrix} Ω_{s}^{i - 1} \end{matrix}$ 近似不变, 或视为一个平均值。ξ ^i-¹的估计与调制方式与SER相关, 由柯西不等式:

$\begin{matrix} \begin{matrix} {|ξ^{i - 1}|}^{2} = {|\frac{1}{P} \overset{P - 1}{\sum_{p = 0}} S_{p} {(ε_{p}^{i - 1})}^{*}|}^{2} < \\ \frac{1}{P^{2}} (\overset{P - 1}{\sum_{p = 0}} {|S_{p}|}^{2}) (\overset{P - 1}{\sum_{p = 0}} {|{(ε_{p}^{i - 1})}^{*}|}^{2}) = \\ σ_{S}^{2} E [{|ε_{p}^{i - 1}|}^{2}] (16) \end{matrix} \end{matrix}$

设 $\begin{matrix} {\{η_{n}^{i - 1}\}}_{n = 0}^{P - 1} \end{matrix}$ 表示时域判决误差, 可以得到:

$\begin{matrix} ε_{p}^{i - 1} = \overset{P - 1}{\sum_{n_{2} = 0}} η_{n}^{i - 1} e^{- j \frac{2 π}{P} np} (17) \end{matrix}$

进而能够得到E $\begin{matrix} [{|ε_{p}^{i - 1}|}^{2}] \end{matrix}$ 表达式为:

$\begin{matrix} \begin{matrix} E [{|ε_{p}^{i - 1}|}^{2}] = \\ E [\overset{P - 1}{\sum_{n_{1} = 0}} \overset{P - 1}{\sum_{n_{2} = 0}} η_{n}^{i - 1} {(η_{n}^{i - 1})}^{*} e^{- j \frac{2 π}{P} (n_{1} - n_{2}) p}] = \\ PE [{|η_{n}^{i - 1}|}^{2}] (18) \end{matrix} \end{matrix}$

根据前面的分析, 判决误差总是将一个符号误判为相邻的符号, 因此时域判决误差只能有4个可能的值, 假设可以表示为± δ 和± jδ , 其中δ 为相邻符号星座图中水平距离或垂直距离。因此, 式(18)可以表示为:

$\begin{matrix} E [{|ε_{p}^{i - 1}|}^{2}] = P Ω_{s}^{i - 1} δ^{2} (19) \end{matrix}$

注意到时域信号功率 $\begin{matrix} σ_{s}^{2} \end{matrix}$ =δ ²/μ , 由式(14)(16)(19)可以得到:

$\begin{matrix} σ_{S}^{- 2} |ξ^{i - 1}| < δ σ_{s}^{- 1} \sqrt{Ω_{s}^{i - 1}} = \sqrt{μ Ω_{s}^{i - 1}} (20) \end{matrix}$

第0次迭代时反馈滤波部分不产生作用, 均衡结构相当于一个由前馈滤波部分构成的线性均衡器, 初始误符号率由前馈线性均衡滤波结构决定。由文献[8]可知, 初始误符号率必须低于一个确定的门限才能可靠地进行后续判决反馈迭代处理。根据这个确定的门限可以预设误符号率Ω _s_{, pre}来简化均衡器系数设计。实际系统中检测点输出信号的误符号率一般要小于或等于0.1, 判决反馈均衡器才能可靠地检测到接收信号并进入迭代收敛状态。通常文献[8]结构的前馈线性滤波器设计即可以满足初始设定SER的值为0.01~0.1, 可以得出理论上 $\begin{matrix} \sqrt{μ Ω_{s}^{i - 1}} \end{matrix}$ ≪1, 因此有如下近似关系:

$\begin{matrix} \begin{matrix} σ_{S}^{2} + ξ^{i - 1} \approx σ_{S}^{2} (21) \\ σ_{S}^{2} + 2 R [ξ^{i - 1}] \approx σ_{S}^{2} (22) \end{matrix} \end{matrix}$

对于给定的星座映射, 接收机设定的信噪比(SNR)门限SNR_pre需要满足预设系统SER的要求, 因此可以通过估计平均SNR的值来确定SNR_pre, 近似得到频域噪声功率 $\begin{matrix} σ_{W}^{2} \end{matrix}$ :

$\begin{matrix} σ_{W}^{2} = σ_{S}^{2} \cdot SN R_{pre}^{- 1} (23) \end{matrix}$

根据式(15), 可以得到 $\begin{matrix} σ_{ε (i - 1)}^{2} \end{matrix}$ ≪ $\begin{matrix} σ_{S}^{2} \end{matrix}$ 。此外, 为有效进行迭代判决反馈处理, 设计参数过程中可先令瞬时误符号率与预设误符号率的值 $\begin{matrix} Ω_{s}^{i - 1} \end{matrix}$ =Ω _s_{, pre}, 只要预设误符号率能使反馈部分可靠地检测到接收信号并进入迭代, 则系统均衡性能将主要取决于信道状态响应对滤波器系数的影响。因此有:

$\begin{matrix} \begin{matrix} σ_{S}^{2} {[σ_{S}^{2} + σ_{ε (i - 1)}^{2}]}^{- 1} = {(1 + μ Ω_{s, pre})}^{- 1} \approx 1 (24) \\ σ_{ε (i - 1)}^{2} {[σ_{S}^{2} + σ_{ε (i - 1)}^{2}]}^{- 1} \approx σ_{ε (i - 1)}^{2} σ_{S}^{- 2} = μ Ω_{s, pre} (25) \end{matrix} \end{matrix}$

式中:对于4QAM、16QAM、64QAM, β 的取值分别为2, 2/5, 2/21。

$\begin{matrix} \begin{matrix} β = σ_{S}^{2} β^{i - 1} \approx \frac{1}{P} \overset{P - 1}{\sum_{p = 0}} \frac{{|H_{p}|}^{2}}{SN R_{pre}^{- 1} + μ Ω_{s, pre} {|H_{p}|}^{2}} (26) \\ α = α^{i} \approx β {[1 + β]}^{- 1} (27) \end{matrix} \end{matrix}$

最后, 经过简化的前馈和反馈滤波器系数可以近似表示为:

$\begin{matrix} \begin{matrix} C_{p} = C_{p}^{i} \approx \frac{(1 - α) H_{p}^{*}}{SN R_{pre}^{- 1} + μ Ω_{s, pre} {|H_{p}|}^{2}} (28) \\ B_{p} = B_{p}^{i} \approx - [C_{p}^{i} H_{p} - α] (29) \end{matrix} \end{matrix}$

对平均信噪比可以采用文献[10]中的M2M4算法进行估计, 提前确定预设信噪比门限。从重新推导的滤波器系数表达式中可以发现, 若信噪比在每个数据块均衡的过程中不发生变化, 则本文算法对确定的信道估计增益每次迭代的滤波器系数为定值。

3 计算复杂度分析及迭代停止准则

文献[8]中的IBDFE算法每次迭代需要估计噪声功率 $\begin{matrix} σ_{_{_{{\hat{S}}^{i - 1}}}}^{2} \end{matrix}$ , 其表达式与该算法复杂度相关:

$\begin{matrix} \begin{matrix} σ_{_{_{{\hat{S}}^{i - 1}}}}^{2} = \frac{1}{P_{S}} \sum_{p \in P_{S}} {|{\hat{S}}_{p}^{i - 1}|}^{2} (30) \\ ρ_{S, {\hat{S}}^{i - 1}} = \frac{1}{P_{S}} \sum_{p \in P_{S}} \frac{R_{p}}{H_{p}} {({\hat{S}}^{i - 1})}_{p}^{*} (31) \end{matrix} \end{matrix}$

式中:P_S为集合S={P: $\begin{matrix} |H_{p}| \end{matrix}$ ≥ H_TH}的基数, H_TH是为了提高估计准确度设置的信道频率响应门限。

设定迭代次数为I, 本文算法与IBDFE在FFT信号处理复杂度上一致, 都需要2(P/2log₂P+P)/I次复乘和2IPlog₂P+P(I-1)复加。注意到频域均衡器运算复杂度不同主要来自于滤波系数计算过程中复乘运算和复加运算的次数, 其中复乘运算又对复杂度起到决定作用。

本文算法与传统IBDFE算法滤波系数计算复杂度如表1所示。当P=512、I=4、P_S=3、M=448时, 定义算法计算复杂度减少比率为:

$\begin{matrix} CCRR = (1 - \frac{本文算法的复杂度}{传统算法的复杂度}) \times 100 % (32) \end{matrix}$

表1 本文算法与传统FD-IBDFE算法复杂度比较 Table 1 Computational complexity of the proposed algorithm and the conventional IBDFE

可以看出, 由于本文提出的算法前馈滤波和反馈滤波系数只计算一次, 对系统复杂度起决定影响的复乘次数减少一半多, 而复加次数则大为减小。因此本文提出的算法复杂度相比IBDFE算法复杂度有明显降低。

随迭代次数增加判决误差功率 $\begin{matrix} σ_{ε (i)}^{2} \end{matrix}$ 会逐渐减小, 令g(i)= $\begin{matrix} σ_{ε (i + 1)}^{2} \end{matrix}$ / $\begin{matrix} σ_{ε (i)}^{2} \end{matrix}$ 为迭代判决函数, T(SNR_pre)是与预设信噪比相关的某个判决门限, 则迭代停止准则为:

$\begin{matrix} g (i) \leq T (SN R_{pre}) (33) \end{matrix}$

4 均衡算法性能仿真

为验证本文提出的低复杂度IBDFE算法性能, 采用九径ITU-EVA信道, 该信道能较好地仿真实际宽带通信环境, 信道参数如表2所示。

表2 ITU-EVA信道模型 Table 2 Channel model of ITU-EVA

相应的系统仿真参数如表3所示, 本文仿真中预设误符号率Ω _s_{, pre}=0.1, 分别在未编码系统和编码系统中对LC-IBDFE算法和传统均衡算法性能进行仿真。为便于比较, 根据预设误符号率和平均信噪比给定统一的预设信噪比门限SNR_pre=10 dB。

表3 SC-FDE系统仿真参数 Table 3 Simulation parameters of SC-FDE system

未编码系统中本文算法与不同均衡算法在ITU-EVA信道下的误码率-信噪比(BER-SNR)曲线如图4所示, 其中括号里标明了迭代次数。可以看出本文提出的LC-IBDFE算法与文献[8]中的传统FD-IBDFE算法性能非常接近, 迭代次数4次以内情况下IBDFE算法相对本文算法增益都小于0.3 dB, 当信噪比高于10的情况下FD-IBDFE算法的性能才略优于本文算法。说明本文算法在大量降低运算复杂度情况下可以较好地近似代替FD-IBDFE算法, 更适合于实际工程应用环境。进行一次迭代后本文算法误码率性能就好于传统的频域线性迫零(ZF)均衡算法及最小均方误差(MMSE)算法, 当迭代两次后本文算法性能已略优于文献[7]中基于MMSE准则的时频混合判决反馈均衡算法(MMSE-HDFE), 而当迭代次数为4且误码率为10^-4时, LC-IBDFE的BER比MMSE-HDFE方法有2.9 dB的增益。

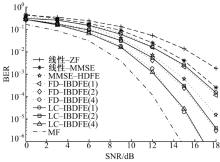	Figure Option View Download New Window
	图4 未编码系统中不同均衡算法的BER-SNR性能比较Fig.4 BER-SNR performance curves of different channel equalization schemes in a non-coded system

图5给出了ITU-EVA信道下卷积编码系统中本文算法与不采用迭代处理的传统频域均衡算法的BER性能比较, 可以看出本文算法在卷积码系统中误码率性能依然好于传统的频域线性均衡算法, 在误码率为10^-4时且迭代4次情况下本文算法相对MMSE-HDFE算法增益为1.4 dB。

	Figure Option View Download New Window
	图5 卷积编码系统中不同均衡算法的BER-SNR性能比较Fig.5 BER-SNR performance curves of different channel equalization schemes in a convolution coded system

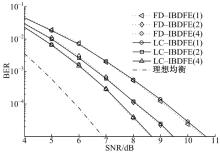
从图6可以看出:卷积编码系统中不同迭代次数下本文算法与IBDFE算法性能非常接近, 在误码率为10^-4情况下均小于0.2 dB。本文算法虽然在对均衡器参数估计过程中进行了简化, 但实际均衡过程中由于迭代运算的收敛性随着迭代次数增加检测可靠性也逐渐增强, 仍然可以较好地逼近FD-IBDFE算法。

	Figure Option View Download New Window
	图6 卷积编码系统中本文算法与IBDFE算法性能比较Fig.6 Performance comparison for the proposed equalization scheme and the IBDFE scheme in a convolution coded system

图7给出了ITU-EVA信道下LDPC编码系统中本文算法与不采用迭代处理的传统频域均衡算法BER性能比较。从图中可以看出, 本文算法在LDPC编码系统中误码率性能依然好于传统频域线性均衡算法, 在误码率为10^-4时且迭代4次情况下本文算法相对MMSE-HDFE算法增益为1.1 dB。可以发现, 在较高编码增益系统中由于受到编码性能影响, 本文算法相对其他非迭代均衡算法的增益要比在低编码增益系统中小。从图8可以看出:LDPC编码系统中不同迭代次数下本文算法与IBDFE算法性能依然非常接近, 在误码率为10^-4情况下SNR差距均小于0.2 dB。

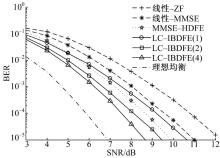	Figure Option View Download New Window
	图7 LDPC编码系统中不同均衡算法的 BER-SNR性能比较Fig.7 BER-SNR performance curves of different channel equalization methods in a LDPC coded system

	Figure Option View Download New Window
	图8 LDPC编码系统中本文算法与IBDFE算法性能比较Fig.8 Performance comparison for the proposed equalization scheme and IBDFE scheme in a LDPC coded system

5 结束语

提出了低复杂度频域迭代块判决反馈均衡(LC-IBDFE)算法, 采用UW序列减少了系统开销, 对每个接收块进行迭代的均衡滤波系数在给定预设信噪比和误符号率情况下只取决于信道冲击响应, 前馈滤波和反馈滤波系数在迭代过程中只计算一次, 算法复杂度比传统的IBDFE算法大量减小。仿真结果表明:与传统的线性ZF及MMSE信道均衡算法相比, 本文提出的低复杂度信道均衡方法可以获得更好的性能, 当迭代次数为4且误码率为10^-4时, LC-IBDFE的BER比MMSE-HDFE方法有大于1 dB的增益, 且相同迭代次数下性能接近传统FD-IBDFE算法。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Sari H, Karam G, Jeanclaude I. Frequency-domain equalization of mobile radio and terrestrial broadcast channels[C]∥IEEE Conference on Global Telecommunications, San Francisco, 1994: 1-5. [本文引用:1]
[2]	Mehana A H, Nosratinia A. Single-carrier frequency-domain equalizer with multi-antenna transmit diversity[J]. IEEE Transactions on Wireless Communications, 2013, 12(1): 388-397. [本文引用:1]
[3]	Silva J, Dinis R, Souto N. Single-carrier frequency domain equalisation with hierarchical constellations: an efficient transmission technique for broadcast and multicast systems[J]. IEEE Communications Letters, 2012, 6(6): 2065-2073. [本文引用:1]
[4]	Li J, Du Y, Liu Y. Comparison of spectral efficiency for OFDM and SC-FDE under IEEE 802. 16 scenarios[C]∥Proceeding of the 11th IEEE Symposium on Computers and Communications, 2006: 467-471. [本文引用:1]
[5]	Hasegawa F, Okazaki A, Kubo H. Novel PAPR reduction scheme for SC-OFDM with frequency domain multiplexed pilots[J]. IEEE Communications Letters, 2012, 16(9): 1345-1348. [本文引用:1]
[6]	Pancaldi F, Vitetta G M, Kalbasi R, et al. Single-carrier frequency domain equalization[J]. IEEE Signal Process Magazine, 2008, 25(9): 37-56. [本文引用:1]
[7]	Falconer D, Ariyavisitakul S L, Benyamin-Seeyar A, et al. Frequency domain equalization for single-carrier broadband wireless systems[J]. IEEE Communications Magazine, 2002, 40(4): 58-66. [本文引用:1]
[8]	Benvenuto N, Tomasin S. Iterative design and detection of a DFE in the frequency domain[J]. IEEE Transactions on Communications, 2005, 53(11): 1867-1875. [本文引用:1]
[9]	Louveaux J, Vand endorpe L, Sartenaer T. Cyclic prefixed single carrier and multicarrier transmission: bit rate comparison[J]. IEEE Communications Letters, 2003, 7(4): 180-182. [本文引用:1]
[10]	Pauluzzi D R, Beaulieu N C. A comparison of SNR estimation techniques for the AWGN channel[J]. IEEE Transactions on Communications, 2000, 48(10): 1681-1691. [本文引用:1]

1994

0.0

... 1994年Sari和Karam等提出了单载波频域均衡(SC-FDE)技术,并受到越来越多的关注^[1,2,3] ...

2013

0.0

... 1994年Sari和Karam等提出了单载波频域均衡(SC-FDE)技术,并受到越来越多的关注^[1,2,3] ...

2012

0.0

... 1994年Sari和Karam等提出了单载波频域均衡(SC-FDE)技术,并受到越来越多的关注^[1,2,3] ...

2006

0.0

... 在未编码系统中单载波频域均衡与OFDM的性能类似^[4],且SC-FDE具有更小的峰均比(PAPR)^[5],对相位噪声的敏感性更低 ...

2012

0.0

... 在未编码系统中单载波频域均衡与OFDM的性能类似^[4],且SC-FDE具有更小的峰均比(PAPR)^[5],对相位噪声的敏感性更低 ...

2008

0.0

... 传统的线性频域均衡器(FD-LE)结构简单、计算复杂度低,但在频率选择性信道中由于噪声的传播均衡性能较差^[6] ...

2002

0.0

... Falconer等提出了时频混合判决反馈均衡算法HD-DFE^[7],HD-DFE由于加入反馈部分,进一步消除了ISI,因而性能强于FD-LE,但由于反馈部分在时域需要进行大量矩阵运算,滤波器系数复杂度和误差随反馈阶数指数增加 ...

2005

0.0

... Benvenuto等提出了频域迭代块判决反馈均衡(FD-IBDFE)算法^[8],该算法中均衡器前馈和反馈滤波部分均在频域实现,通过FFT变换相对时频混合结构降低了运算复杂度,且在多次迭代后性能较好,但该算法每次迭代都要重新计算滤波系数,并对多个参数进行估计,在迭代次数增加后仍然具有较高复杂度 ...

2003

0.0

... 本文给出一种低复杂度频域迭代判决反馈均衡(LC-IBDFE)算法,采用特殊字序列UW做为循环前缀^[9],并起到信道跟踪的作用,单载波系统接收机不需要删除接收信号中的UW对应部分,可以直接进行串/并转换和FFT进而减小了系统开销 ...

2000

0.0