可见光通信中低复杂度自适应广义空间调制算法

引用本文

朱义君, 付红双, 蔡文炳. 可见光通信中低复杂度自适应广义空间调制算法. 2015, 45(6): 2080-2084
ZHU Yi-jun, FU Hong-shuang, CAI Wen-bing. Low complexity adaptive generalized spatial modulation for visible light communication. Journal of Jilin University Engineering and Technology Edition, 2015, 45(6): 2080-2084 复制到剪切板

Permissions

可见光通信中低复杂度自适应广义空间调制算法

朱义君¹, 付红双¹, 蔡文炳²

1.中国人民解放军信息工程大学信息系统工程学院,郑州 450002

2. 北京跟踪与通信技术研究所,北京 100094

作者简介:朱义君(1976-),男,副教授,博士.研究方向:通信中的信号处理与可见光通信.E-mail:xxgczhu@126.com

基金:“863”国家高技术研究发展计划项目(2013AA013603)

摘要

针对可见光信道相关性较大的问题,以成对错误概率为依据提出了一种自适应广义空间调制(Adaptive GSM,AGSM)算法,发送端能够根据信道状态信息(Channel state information,CSI)对GSM系统中的天线组和各天线组的调制阶数进行联合优化以提高GSM算法的误码率性能。但由于该优化算法的运算复杂度较大,又提出了一种简便的自适应空间调制(Simplified AGSM,S-AGSM)算法,利用QR分解限制穷举搜索的空间,降低了优化算法的复杂度。仿真结果表明:在同样频带利用率的情况下,S-AGSM算法的误码率性能要优于GSM算法和只带有天线组选择的GSM系统,且复杂度远小于AGSM算法。

关键词: 通信技术; 可见光通信; 广义空间调制; 自适应调制; 信道相关性

中图分类号:TN929.12 文献标志码:A 文章编号:1671-5497(2015)06-2080-05

Low complexity adaptive generalized spatial modulation for visible light communication

ZHU Yi-jun¹, FU Hong-shuang¹, CAI Wen-bing²

1.Institute of Information System Engineering,PLA Information Engineering University,Zhengzhou 450002,China

2.Beijing Institute of Tracking and Telecommunication Technology,Beijing 100094,China

Abstract

Aiming at the high correlation of optical channel, an Adaptive Generalized Spatial Modulation (AGSM) algorithm was proposed based on the pair error probability of GSM. The antenna combinations and modulation levels were optimized jointly based on the Channel State Information (CSI) for better Bit Error Rate (BER) performance. The computational complexity of the AGSM was high, so a Simplified AGSM (S-AGSM) was then put forward. The S-AGSM utilizes QR decomposition to limit the exhaustive search space, thus to lower the computational complexity. Simulation results show that the S-AGSM performs better than GSM and GSM with only antenna selection. Moreover, S-AGSM has lower complexity than AGSM.

Keyword: communication; visible light communications; generalized spatial modulation; adaptive modulation; channel correlation

Show Figures

0 引言

可见光通信(Visible light communications, VLC)是一种工作在可见光光谱范围内的新兴高速短距离通信技术, 在照明产业升级换代的近十年来发展尤为迅速, VLC能够很好地解决末端接入和深度覆盖的问题。由于强度调制/直接检测(Intensity modulation/direct detection, IM/DD)方式较为简便、易于实现, 所以目前大多数VLC系统都采用IM/DD方式。但这种方式忽略了信号的频率信息和相位信息, 直接导致了室内光MIMO(Multiple input multiple output)信道的相关性比传统无线信道大得多^[1]。

空间调制(Spatial modulation, SM)是一种新型的空间复用方式, 利用发送天线的空间位置传递信息。SM技术最早由Hass等提出^{[2, 3]}, 并已成功运用到VLC中^[3]。由于每个时刻只有一个天线被激活, 因此SM完全避免了天线间同步及信道间干扰等问题, 尤其适用于高相关性的可见光信道中。为了提高SM的频带利用率, Fu等^[4]提出了广义空间调制(GSM)技术。

为了降低信道相关性对空间调制系统性能的影响, 通常需要选择合适的发送天线和调制阶数。文献[5]提出了一种空间调制中天线子集选择方法, 但是该方法需要穷尽搜索, 复杂度较大。文献[6]利用空间调制的特殊传输方式, 提出了一种只针对恒模调制的低复杂度调制阶数选择方法。文献[7]提出了一种缩减搜索范围的简化调制阶数选择算法, 只在出现概率较大的调制方案集中进行搜索, 因此有一定的性能损失, 且不适用于确定性的可见光信道中。文献[8, 9]通过构造欧氏距离矩阵并且利用结式矩阵的性质减小了天线选择的复杂度。文献[10]提出了一种基于自适应选择调制阶数和发送天线数的最优空间调制模式, 同时也给出了一种低复杂度的次优混合空间调制模式, 即先选择发送天线, 再对调制阶数进行优化, 这同样会带来性能上的损失。

基于以上研究现状, 为了增强GSM系统的误码率性能, 本文提出了一种自适应广义空间调制(AGSM)技术, 根据信道状态信息(Channel state information, CSI), 实时动态调整工作的天线组和各天线组的调制阶数。另外, 本文还提出了一种基于QR分解的简化自适应广义空间调制(S-AGSM)算法, 在保证性能不变的基础上大大降低了算法复杂度。

1 系统模型

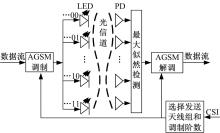
AGSM系统模型如图1所示。首先接收端对CSI进行估计并根据CSI对发送天线组和调制阶数进行自适应选择, 然后将选择的结果传递给发送端。发送端接收到反馈的AGSM映射方式, 首先根据前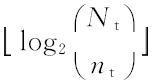个比特确定工作的天线组k, 然后将其后的logd_k(d_k为第k个天线组的调制阶数)个比特映射为信号x_q, 再根据随后的个比特确定下一时刻的工作组, 如此循环至数据流结束。在接收端利用最大似然(Maximum likelihood, ML)检测算法检测出天线组合序号以及各天线所发送的符号, 最后经过AGSM解调模块恢复出初始二进制比特数据流。

	Figure Option View Download New Window
	图1 自适应广义空间调制技术框图Fig.1 Block diagram of adaptive generalized spatial modulation

某一时刻的接收信号矢量可以表示为:

$\begin{matrix} y = \sqrt{\frac{ρ}{n_{t}^{2}}} H x_{j, eff, q} + n = \sqrt{\frac{ρ}{n_{t}^{2}}} h_{j, eff} x_{q} + n (1) \end{matrix}$

式中:h_j_{, eff}=h_j₍₁₎+h_j₍₂₎+…+ $\begin{matrix} h_{j (n_{t})} \end{matrix}$ , h_j_{(· )}为归一化信道矩阵的特定列; ρ 为接收端信噪比; n为N_r维高斯白噪声, n~CN(0, 1)。

接收端利用ML准则对发送信号矢量进行检测译码, 检测得到的天线组序号和发送符号为:

$\begin{matrix} \begin{matrix} [\tilde{j}, \tilde{q}] = \underset{j, q}{argmin} ‖ y - \sqrt{ρ'} g_{j, q} ‖_{F}^{2} = \\ \underset{j, q}{argmin} [\sqrt{ρ'} ‖ g_{j, q} ‖_{F}^{2} - 2 (y^{T} g_{j, q})] (2) \end{matrix} \end{matrix}$

式中:‖ · ‖ _F为矩阵或向量的Frobenius范数; 记g_j_,_q=h_j_{, eff}x_q; ρ '=ρ / $\begin{matrix} n_{t}^{2} \end{matrix}$ , ρ 为接收端平均信噪比。

发送信号矢量为 $\begin{matrix} x_{j_{eff}, q} \end{matrix}$ , 接收端检测得到的发送信号矢量为 $\begin{matrix} x_{{_{\hat{j}}}_{eff},_{\hat{q}}} \end{matrix}$ 的成对错误概率为:

$\begin{matrix} \begin{matrix} PEP (x_{j, q} \to x_{\tilde{j}, \tilde{q}}) = \\ P {\sqrt{ρ'} ‖ g_{j, q} ‖_{F}^{2} - 2 (y^{T} g_{j, q}) > \\ \sqrt{ρ'} ‖ g_{\hat{j}, \hat{q}} ‖_{F}^{2} - 2 (y^{T} g_{\hat{j}, \hat{q}})} = \\ P {n^{T} (g_{\hat{j}, \hat{q}} - g_{j, q}) > \\ \frac{\sqrt{ρ'}}{2} ‖ g_{j, q} - g_{\hat{j}, \hat{q}} ‖_{F}^{2}} = \\ Q (\sqrt{ρ' / 4 ‖ g_{j, q} - {g_{\hat{j}}}_{, \hat{q}} ‖_{F}^{2}}) (3) \end{matrix} \end{matrix}$

式中:Q(x)= $\begin{matrix} (1 / \sqrt{2 π}) \end{matrix} \begin{matrix} \int_{x}^{+} \end{matrix}$ exp $\begin{matrix} (- t^{2} / 2) \end{matrix}$ dt。

因此, 系统误码率上限为:

$\begin{matrix} \begin{matrix} p_{e, bit}^{UB} = \\ \frac{1}{Kd} \overset{d_{j}}{\sum_{q = 1}} \overset{K}{\sum_{j = 1}} \overset{d_{\hat{j}}}{\sum_{\hat{q} \neq q = 1}} \overset{K}{\sum_{\hat{j} \neq j = 1}} \\ N (x_{j, q}, {x_{\hat{j}}}_{, \hat{q}}) PEP (x_{j, q} \to {x_{\hat{j}}}_{, \hat{q}}) (4) \end{matrix} \end{matrix}$

式中:N $\begin{matrix} (x_{j, q}, {x_{\hat{j}}}_{, \hat{q}}) \end{matrix}$ 为符号x_j_,_q和符号 $\begin{matrix} {x_{\hat{j}}}_{, \hat{q}} \end{matrix}$ 的比特差异数; K为天线组合数; d为K个天线组的平均调制阶数, 可表示为d_sum= $\begin{matrix} {(\overset{K}{\prod_{k = 1}} d_{k})}^{\frac{1}{K}} \end{matrix}$ , d_k为第k个天线组合的调制阶数。

设调制方式d=[d₁, d₂, …, d_K], 其共有l= $\begin{matrix} (\begin{matrix} K + Klo g_{2} d_{sum} - 1 \\ K - 1 \end{matrix}) \end{matrix}$ 种取值, 例如, 当频带利用率为3 bits/s/Hz时, 设N_t=4, n_t=2, 则K=4, d有[1, 1, 1, 16]…[16, 1, 1, 1]等共35种取值。当d₁=…=d_k时, 即各天线组的调制阶数相同时AGSM退化为GSM。

2 自适应广义空间调制

由于GSM系统中通常有 $\begin{matrix} (\begin{matrix} N_{t} \\ n_{t} \end{matrix}) \end{matrix}$ > K, 因此为了提高GSM系统性能, 一方面可以根据CSI选择发送天线组; 另一方面可以根据CSI选择每个天线组合的调制阶数, 即n_t个天线发送相同的数据, 但每个天线组合的调制阶数不同。

2.1 天线组与调制阶数联合优化

根据GSM的映射规则, 一部分比特决定哪个天线组工作, 另一部分比特决定这些天线组合发送什么样的数据, 因此GSM的频带利用率为:

$\begin{matrix} m = lo g_{2} (d_{sum} \times K) (5) \end{matrix}$

为了保证频带利用率m是整数, 要求d和K都必须是2的幂次, K= 。在AGSM中, 为了能够得到更优的误码率性能, 工作天线组以及每个天线组合的调制阶数可以根据CSI动态分配, 由式(3)可知接收信号的欧式距离在成对错误概率中起到了决定性作用, 故采用最小欧式距离最大化准则对发送天线组和调制阶数进行选择, 得到的最优天线组合与调制阶数表示为:

$\begin{matrix} [\hat{a}, \hat{d}] = \underset{g, d}{argmax} d_{\min} (H) (6) \end{matrix}$

式中:最小欧式距离d_min(H)定义为:

$\begin{matrix} d_{\min} (H) = \min_{x_{i_{eff, p}}, x_{j_{eff, q}} \in S} ‖ H (x_{i_{eff, p}} - x_{j_{eff, q}}) ‖_{F}^{2} (7) \end{matrix}$

式中:S代表所有发送信号矢量的集合。

由于式(7)的解析表达式难以求解, 只能对信号s_i和s_j的可能取值进行穷尽搜索。

2.2 低复杂度AGSM(S-AGSM)

由于上述的发送天线组和调制阶数联合优化算法的复杂度较高, 这里介绍一种低复杂度的自适应算法。式(7)可以写为:

$\begin{matrix} \begin{matrix} d_{\min} (H) = \min_{x_{p}, x_{q} \in X} ‖ h_{i_{eff}} x_{p} - h_{j_{eff}} x_{q} ‖_{F}^{2} = \\ \min_{x_{p}, x_{q} \in X} {||[\begin{matrix} h_{i_{eff}} & h_{j_{eff}} \end{matrix}] [\begin{matrix} x_{p} \\ - x_{q} \end{matrix}]||}_{F}^{2} (8) \end{matrix} \end{matrix}$

式中:X为信号x_p、x_q的取值空间。

对信道矩阵 $\begin{matrix} [h_{i_{eff}} h_{j_{eff}}] \end{matrix}$ 进行QR分解得到 $\begin{matrix} [h_{i_{eff}} h_{j_{eff}}] \end{matrix}$ QR=Q $\begin{matrix} [\begin{matrix} k_{11} & k_{12} \\ k_{22} \end{matrix}] \end{matrix}$ 。由于Q为酉矩阵, 式(8)可以表示为:

$\begin{matrix} \begin{matrix} d_{\min} (H) = \min_{x_{p}, x_{q} \in X} {||R [\begin{matrix} x_{p} \\ - x_{q} \end{matrix}]||}_{F}^{2} = \\ \min_{x_{p}, x_{q} \in X} {||[\begin{matrix} k_{11} x_{p} - k_{12} x_{q} \\ - k_{22} x_{q} \end{matrix}]||}_{F}^{2} (9) \end{matrix} \end{matrix}$

为了使 $\begin{matrix} {||R [\begin{matrix} x_{p} \\ - x_{q} \end{matrix}]||}_{F}^{2} \end{matrix}$ 最小, 令k₁₁x_p-k₁₂x_q=0, 这就在信号x_p和信号x_q之间建立了联系, 因此信号x_p的取值可以由信号x_q确定, 只需对信号x_q穷举搜索即可。为了缩减x_q的搜索范围, 假定x_q是与调制阶数min(d_i, d_j)相对应的符号。

由于在SM中当I_m=0时, 天线的空间位置会全部丢失, 此时不能传递任何信息, 而且LED的单向导电性要求调制LED的信号为非负, 故在平均光功率一定的条件下, M阶PAM调制的强度为:

$\begin{matrix} I_{m} = \frac{2 x}{M + 1} mform = 1, 2, \dots, M (10) \end{matrix}$

式中:x为平均光功率, 本文假设平均功率为1。因而信号x_p可以表示为:

$\begin{matrix} \begin{matrix} {\hat{x}}_{p} = \frac{1}{M + 1} \max (\frac{2}{(M + 1)}, \\ \min (\frac{2 M}{M + 1}, 2 rnd (\frac{(M + 1) k_{12} x_{q}}{2 k_{11}}))), \\ M = \max (d_{i}, d_{j}) (11) \end{matrix} \end{matrix}$

式中:M为信号x_p的调制阶数; 2rnd $\begin{matrix} (\frac{(M + 1) k_{12} x_{q}}{2 k_{11}}) \end{matrix}$ 是为了得到与 $\begin{matrix} \frac{k_{12} x_{q}}{k_{11}} \end{matrix}$ 最接近的偶数; max $\begin{matrix} (\frac{2}{M + 1}, \min (\frac{2 M}{(M + 1)}, z)) \end{matrix}$ 是为了使信号z不超出N阶PAM调制信号的星座点范围。因此, d_min(H)可以表示为:

$\begin{matrix} d_{\min} (H) = \min_{x_{q} \in X} ‖ h_{i_{eff}} {\hat{x}}_{p} - h_{j_{eff}} x_{q} ‖_{F}^{2} (12) \end{matrix}$

对于每一个天线组集, d_min(H)具体计算流程图如图2所示。

	Figure Option View Download New Window
	图2 最小欧式距离计算流程图Fig.2 Flow diagram of minimum Euclidean distance

2.3 复杂度分析

下面对AGSM算法和S-AGSM算法的复杂度进行对比分析, 本文中算法复杂度定义为每个天线组集中计算欧式距离的次数。在m值较大时, 按式(6)对AGSM系统所有可能的发送符号进行穷尽搜索的计算量相当大, 需要在l种调制阶数中进行搜索, 算法复杂度为:

$\begin{matrix} \overset{d_{(\begin{matrix} K + Klo g_{2} d - 1 \\ k - 1 \end{matrix})}}{\sum_{d = d_{1}}} \overset{K}{\sum_{i = 1}} \overset{K}{\sum_{j = i + 1}} d_{i} d_{j} \end{matrix}$

由于本文提出的S-AGSM算法中在信号x_p和信号x_q之间建立了联系, 可以用信号x_q表示信号x_p, 因此只需对信号x_q进行穷尽搜索即可, 故S-AGSM的复杂度为:

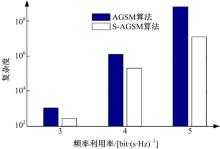
$\begin{matrix} \overset{d_{(\begin{matrix} K + Klo g_{2} d - 1 \\ k - 1 \end{matrix})}}{\sum_{d = d_{1}}} \overset{K - 1}{\sum_{i = 1}} \overset{K}{\sum_{j = i + 1}} \min (d_{i}, d_{j}) \end{matrix}$

图3对比了频带利用率3~5 bits· (s· Hz)^-1情况下AGSM和S-AGSM两种算法的复杂度。可以看出, S-AGSM算法的复杂度远远小于AGSM, 例如当m=4 bits· (s· Hz)^-1, K=8, d=2时, AGSM和S-AGSM的复杂度分别为2.5× 10⁵和1.6× 10⁶。而且频带利用率越大, S-AGSM算法的优势越明显。

	Figure Option View Download New Window
	图3 AGSM和S-AGSM算法复杂度对比Fig.3 Complexity comparison of AGSM and S-AGSM

3 仿真结果分析

由于AGSM调制中每组天线的调制阶数不同, 发送比特向量的维数与接收比特向量的维数有可能不相等, 所以需要以最长数据分组(log₂K+log₂d_max, d_max为向量d中最大的元素)为基准向信息位的末端填充“ 0” , 使得收发比特向量的维数相等, 以便能够正确解码、防止错误传播。

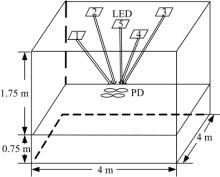
该部分对5× 4AGSM通信系统的误码率性能进行了蒙特卡罗仿真, 仿真数据量为1× 10⁵, 信道参数为:聚光器折射率n=1.5; LED的半功率角 $\begin{matrix} φ_{\frac{1}{2}} \end{matrix}$ =60° ; 光学滤波器增益T(ψ )=1; PD的视场角FOV为60° ; PD的接收面积A=1 cm²。LED及PD分布在4 m× 4 m的房间内, 如图4所示, 表1给出了发送端LED以及接收端PD的具体位置。

	Figure Option View Download New Window
	图4 室内VLC收发端布局示意图Fig.4 Layout of transceivers for indoor VLC

表1 LED及PD的位置 Table 1 Positions of LEDs and PDs

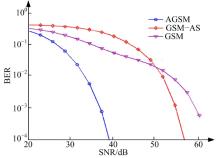
图5对比了传统GSM、AGSM以及利用文献[8]中的天线选择算法进行天线选择的GSM-AS系统在频带利用率为4 bit· (s· Hz)^-1时的误码率性能(N_t=5, n_t=2)。可以看出, 在误比特率为10^-4时, AGSM的误码率性能最优, 传统GSM系统的误码率性能最差, AGSM系统较GSM-AS系统可以获得17 dB以上的性能增益(注:文中只仿真对比了特定信道下的系统性能, 具体性能增益还与具体信道有关), 这也证明了文中所提自适应算法的有效性。

	Figure Option View Download New Window
	图5 AGSM、GSM和GSM-AS性能对比Fig.5 Performance comparison of AGSM, GSM and GSM-AS

4 结束语

提出了一种基于接收信号最小、欧式距离最大化准则的自适应广义空间调制技术, 根据CSI动态选择天线组和各天线组的调制阶数, 该算法较只带有天线组选择的GSM系统可以获得17 dB以上的性能增益, 比GSM系统可以获得21 dB以上的性能增益。但是在频带利用率较高时, 该自适应算法复杂度过高, 于是本文又给出了一种低复杂度的S-AGSM算法, 该算法利用QR分解限制了穷尽搜索的空间, 降低了计算量并且保持了与AGSM算法相同的性能。数值计算结果表明, 频带利用率越高, S-AGSM系统的复杂度优势越明显。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	付红双, 朱义君. 室内直射环境下白光LED的多输入多输出信道相关性分析[J]. 光学学报, 2013, 33(9): 0906002. Fu Hong-shuang, Zhu Yi-jun. Analysis of the correlation of optical multiple-input multiple-output channel using white LED lighting in indoor line of sight environments[J]. Acta Optica Sinica, 2013, 33(9): 0906002. [本文引用:1]
[2]	Mesleh R Y, Hass H, Sinanovic S, et al. Spatial modulation[J]. IEEE Transactions on Vehicular Technology, 2008, 57(4): 2228-2241. [本文引用:1]
[3]	Fath T, Hass H, Marco D, et al. Spatial modulation applied to optical wireless communications in indoor LOS environments[C]∥Proceedings of the Global Communications Conference, Houston, TX, USA, 2011: 1-5. [本文引用:2]
[4]	Fu J L, Hou C P, Xiang W, et al. Generalised Spatial modulation with multiple active transmit antennas[C]∥IEEE Globecom Workshop on Broadband Wireless Access, Houston, Texas, USA, 2010: 839-844. [本文引用:1]
[5]	Ntontin K, Renzo M D, Perez-Neira A, et al. Antenna subset selection for spatial modulation: a novel and energy efficient single RF technique[C]∥IEEE International Conference on Communications, Gulin, China, 2013: 2454-2458. [本文引用:1]
[6]	Yang P, Xiao Y, Yu Y, et al. Adaptive spatial modulation for wireless MIMO transmission systems[J]. IEEE Communications Letters, 2011, 15(6): 602-604. [本文引用:1]
[7]	Yang P, Xiao Y, Yu Y, et al. Simplified adaptive spatial modulation for limited-feedback MIMO systems[J]. IEEE Transactions on Vehicular Technology, 2013, 64(6): 2656-2666. [本文引用:1]
[8]	Rajashekar R, Hari K V S, Hanzo L. Antenna selection in spatial modulation systems[J]. IEEE Communications Letters, 2013, 17(3): 521-524. [本文引用:1]
[9]	Pillay N, Xu H J. Comments on “antenna selection in spatial modulation systems”[J]. IEEE Communications Letters, 2013, 17(9): 1681-1683. [本文引用:1]
[10]	Yang P, Xiao Y, Li L, et al. Link adaptation for spatial modulation with limited feedback[J]. IEEE Transactions on Vehicular Technology, 2012, 61(8): 3808-3813. [本文引用:1]

2013

0.0

. 2013, 33(9):0906002-

Analysis of the correlation of optical multiple-input multiple-output channel using white LED lighting in indoor line of sight environments

室内直射环境下白光LED的多输入多输出信道相关性分析

Fu Hong-shuang , Zhu Yi-jun.

付红双, 朱义君

可见光通信是一种工作在可见光光谱范围内的新兴高速短距离通信技术。将白光LED作为光源的光无线网络中,通常使用强度调制/直接检测方式,忽略了信号的频率和相位信息,导致光无线信道的空间相关性比传统无线信道大得多。分析了影响光多输入多输出(MIMO)信道相关性的因素,并通过仿真验证了在特定条件下各因素对信道相关性产生影响的方式。在特定的场景内,根据信噪比和信道相关性的共同影响获得了最佳的收发端参数设置,从而得到了最佳的误码率性能。

... 但这种方式忽略了信号的频率信息和相位信息,直接导致了室内光MIMO(Multiple input multiple output)信道的相关性比传统无线信道大得多^[1] ...

2008

0.0

... SM技术最早由Hass等提出^[2,3],并已成功运用到VLC中^[3] ...

2011

0.0

... SM技术最早由Hass等提出^[2,3],并已成功运用到VLC中^[3] ...

2010

0.0

... 为了提高SM的频带利用率,Fu等^[4]提出了广义空间调制(GSM)技术 ...

2013

0.0

2011

0.0

2013

0.0

2013

0.0

2013

0.0

2012

0.0