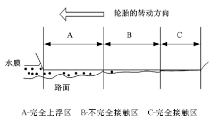
“ 滑水现象” 如图1所示, A为水膜区, B为过渡区, C为直接接触区。轮胎滚动时, 由于水的惯性, 接触面前部的水需要一定时间排出。速度快时, 轮胎将迅速排挤水层, 由于惯性挤压的水膜将形成动压升力。随着速度提高, 动压升力随之升高, 直至与载荷平衡, 形成完全的水膜区, 即B、C区消失。轮胎滑水符合动压润滑油膜的3个条件:①两个表面之间有相对运动; ②两表面之间有楔形间隙, 润滑油从大口进入, 小口流出; ③两表面之间润滑剂有一定的黏度。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 滑水现象原理图Fig.1 Hydroplaning mechanism

另一方面轮胎滑水属于弹流润滑问题^{[6, 7]}。由于轮胎由较软的橡胶材料组成, 轮胎水膜的压力对胎面的变形将不可忽略, 而胎面的变形将反过来影响压力的分布, 因此轮胎的动力滑水属于复杂的流固耦合问题, 在润滑系统里亦称之为弹流动力润滑(EHL)。

影响轮胎滑水性能的因素有很多, 诸如水膜厚度、车速、胎压、胎面花纹几何形状和深度等。

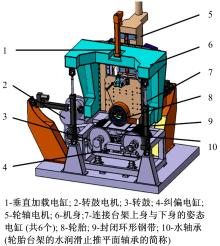
本文钢带式高速轮胎试验台结构如图2所示。图中机身6、轮轴电机5、垂直加载电缸1、轮胎8组成台架上半身; 转鼓3、转鼓电机2、钢带9、水轴承10、纠偏电缸4组成台架下半身, 亦称为高速模拟路面系统; 图中对应的6个电缸7分别连接台架上半身与下半身, 来实现轮胎的各个姿态, 模拟轮胎侧倾、侧偏各个工况^[2]。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 高速轮胎试验台机理Fig.2 Mechanism of high-speed tire test rig

通过转鼓电机2带动转鼓3, 使钢带9旋转来模拟高速运转的路面系统; 通过轮轴电机5带动轮胎旋转来模拟轮胎速度; 连接台架上身与下身的姿态电缸7可调节轮胎姿态, 模拟侧倾、侧偏工况。纠偏电缸4可实时调节高速时钢带9位置, 防止跑出。

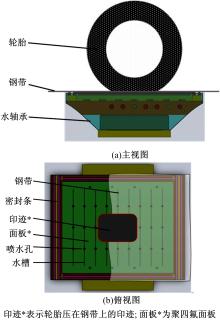
另外, 为防止轮胎8在施加垂直载荷时, 使钢带9产生过大的弯曲变形, 使其不再是平面, 因此需在钢带9的下方安置水轴承10来支撑钢带, 如图3所示。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 水轴承系统结构图Fig.3 Construction drawing of water bearing

在台架高速运转时, 图3中水轴承的面板与钢带之间将存在较大的滑移, 导致不利的摩擦、磨损。因此需在两者之间建立一层水膜来润滑。

由于钢带很薄、易变形, 该水轴承不同于常规的静压止推轴承, 接触区四周的变形量将会降低静压效果^[8]。可以将轮胎滑水机理应用在该处, 因为它同样具备动压润滑的三大条件。在达到一定速度时, 钢带与水轴承面板之间将形成动压水膜, 避免摩擦、磨损, 并且需在较低的临界车速下形成完全的水滑效应。

2.1.1 轮胎的等效弹性模量的估算

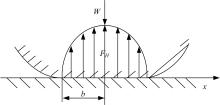
温诗铸等在文献[9]中指出材料的弹性模量对润滑影响是显著的; 另外, Herrebrugh^[10]研究了橡胶、塑料等大弹性材料的弹流问题, 发现弹性模量是一个重要的影响因素, 并推导出大弹性材料的弹流膜厚经验公式, 因此, 轮胎的等效弹性模量的估算是较为重要的。另外, 用Hertz弹性接触理论估算接触区半宽b时(见式(1)), 同样需知轮胎的等效弹性模量E', 如图4所示。

b=8wR/πE'1

式中:b为接触区半宽; w为线载荷; R为轮胎半径; E'为当量弹性模量。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 赫兹压力分布Fig.4 Hertz pressure distribution

在接触区的接触应力依照半椭圆规律分布, 即

F=FH1-x2/b22

式中:F为接触应力; F_H为最大接触应力; x为纵向方向的坐标。

可推出:

FH=2w/(πb)=E'b/4R3

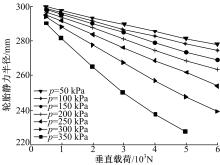
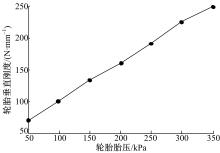
图5为某个国产品牌的轮胎(型号175/70 R14), 不同胎压下的径向刚度试验曲线。图6为轮胎垂直刚度与胎压关系的试验曲线。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 不同胎压下垂直刚度曲线Fig.5 Vertical stiffness under different tire pressure

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 垂直刚度随胎压变化关系Fig.6 Relationship between vertical stiffness and pressure

从图6试验数据可知, 轮胎的垂直载荷与垂直变形量近似呈线性关系, 垂直刚度与胎压也近似呈线性关系。可得:

F'=KΔz4

式中:F'为垂直载荷; K为垂直刚度; Δ z为轮胎垂直方向压缩量。

K=c1p+c25

式中:p为轮胎胎压; c₁、c₂为拟合系数, 此处可分别取0.6 m、40 N/mm。

根据圆的几何性质, 可得:

b2=2RΔz6

由式(4)(6)得:

K=2RF'/b2=2RwB/b27

式中:B为轮胎的宽度。

由式(3)得:

E'=4RFH/b=8wR/(πb2)(8)

对比式(7)(8), 并考虑式(5), 可得轮胎等效弹性模量E'与垂直刚度、轮胎胎压的关系如下:

E'=4πBK=4πBc1p+c29

该轮胎标准胎压为220 kPa, 轮胎胎宽为175 mm, 代入式(9), 可得等效弹性模量为1.3 MPa, 而实际轮胎橡胶为填充后的橡胶, 弹性模量在1~10 MPa左右, 因此该轮胎综合等效的弹性模量与橡胶常态下弹性模量在数量级上是基本吻合的。

根据前面模型简化, 钢带与轮胎等效为包裹光滑钢带面的轮胎。钢带与轮胎类似于串联的两个弹簧, 由于钢带弹性模量为210 GPa, 因此相对总的弹性模量, 钢带弹性模量的影响可忽视。

2.1.2 线接触弹流的流固耦合方程

当光滑胎面与刚性平面之间充有薄膜液体时, 该动压水膜的Reynolds方程为:

ddxρh3ηdpwdx=12Udρhdx10

式中:ρ 为液体(这里为纯净水)的密度; h为水膜厚度; η 为纯净水的粘度; p_w为水膜压力; U为两个平面的速度平均值。

Reynolds方程的边界条件为:进口压力为0, 出口压力和压力导数均为0。

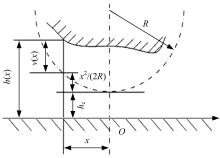
图7为线接触间隙形状。膜厚方程为:

h(x)=hc+x2/(2R)+v(x)(11)

式中:h(x)为水膜厚度; h_c为没有变形时的中心膜厚, 根据载荷平衡条件来确定; v(x)为由压力产生的弹性变形位移。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 水膜间隙形状Fig.7 Shape of water film clearance

变形方程为:

v(x)=- 2πE'∫x0xep(s)ln(s-x)²ds+c (12)

式中:s为x轴上的附加坐标, 它表示任意线载荷p(s)ds与坐标原点的距离; p(s)为坐标压力分布; x₀与x_e为载荷p(x)作用起点与终点的坐标; c为待定系数; E'为当量弹性模量, 此处为轮胎等效弹性模量。

载荷方程为:

w=∫x0xep(s)ds13

因为轮胎滑水的压力远小于0.02 GPa, 因此无需考虑黏压方程与密压方程。

2.2.1 流固耦合的计算思路与流程

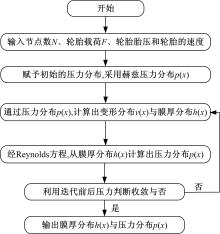
本文采用顺解法来解决该流固耦合问题, 即通过初始的赫兹压力分布p(x)求解出弹性变形方程与膜厚方程h(x)。然后再将h(x)代入Reynolds方程计算出p(x), 如此反复计算, 直到p(x)、h(x)趋于定值, 即收敛。具体流程如图8所示。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 仿真流程图Fig.8 Flow chart of simulation

2.2.2 压力与膜厚的迭代算法

为解算方便, 需对上述方程进行无量纲化, 采用如下的无量纲。具体可参见文献[11], 本文不再复述。

设膜厚参数H=hR/b²; 线载荷参数W=w/(E'R); 速度参数U=η ₀u/(E'R); 材料参数G=α E'; 坐标参数X=x/b; 压力参数P=F/F_H; 可得压力的无量纲方程如下:

ddXεdPdX=dHdX14

式中:ε =H³F_Hb³/(12η ₀UR²)。

采用中心和向前差分格式离散公式(14), 可得离散后的差分方程

εi-1/2Pi-1-(εi-1/2+εi+1/2)Pi+εi+1/2Pi+1ΔX2=Hi-Hi-1ΔX15

式中:ε _{i± 1/2}=1/2(ε _i+ε _{i± 1}); Δ X=X_i-X_i-1。

本文采用如下的压力修正方法:

Pi¯=P~i+c1δi16

式中:c₁为松弛因子; δ _i为压力修正因子; Pi¯和 P~i分别为迭代修正前、后的压力。

对Gauss-Seidel迭代法

δi=(∂Li∂Pi)-1γi¯17

式中: ∂Li∂Pi=- εi-1/2+εi+1/2ΔX2+ 1πKi, i-Ki-1, iΔX;

γi¯=- εi-1/2Pi-1-(εi-1/2+εi+1/2)Pi+εi+1/2Pi+1ΔX2+

Hi-Hi-1ΔX;

K_{i, i}, K_{i-1, i}为变形系数, 可参见文献[12]。

同样可得出, 载荷的离散无量纲方程

ΔX∑i=1nPi+Pi+12=π218

载荷平衡条件是通过修正刚体位移H₀来改变压力值间接完成的, 方法如下:

H-0= H~0+[1- ΔXπ∑i=1n(P_i+P_i+1)]φ (19)

式中: H-0、 H~0是前文中心膜厚h_c对应的迭代修正前、后无量纲数值; φ 为膜厚修正因子, 此处可采用赫雷布勒^[10](Herrebrugh, K)公式, 即

φ=3.01U0.6W-0.220

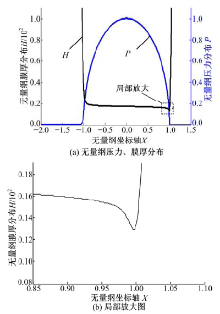
图9为完全滑水情况下的压力分布和水膜膜厚分布。仿真条件如下:轮胎型号为某个国产品牌175/70 R14; 胎宽为0.175 m; 半径为0.3 m; 载荷为4000 N; 胎压为220 kPa; 水黏度η 为0.001 Pa· s; 车速为10 m/s; 节点数为3500; 无量纲起始点坐标X₀为-2; 无量纲终点坐标X_e为1.5。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 滑水模型的压力与膜厚分布Fig.9 Distribution curves of pressure and film thickness

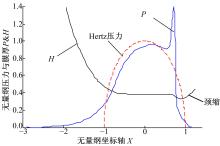
图10为文献[9]中的典型弹流压力与油膜形状分布曲线。从图9中可知典型弹流润滑问题具有以下特征^[11]:①在接触区中部, 水膜呈近似平行状; ②在出口处, 油膜开始收缩, 形成出口区的颈缩现象, 紧缩处的膜厚为最小水膜厚度h_min; ③在出口区, 与颈缩处对应处, 存在二次压力峰。

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 文献中[9]典型的压力分布与油膜形状Fig.10 Typical curves of pressure and film thickness in Ref.[9]

对比图9与图10可知, 滑水模型仿真结果与典型特征①、②相吻合, 但特征③的“ 二次压力峰” 却不明显。分析原因可能如下, Houpert在NASA文献[12]中表明:二次压力峰随无量纲载荷的增大而衰减, 在文中当无量纲载荷取3× 10^-3时, 二次压力峰基本消失。对比文本中无量纲载荷W=w/(E'R)而言, 数量级在10^-2左右, 解释了二次压力峰消失的原因。因此, 仿真结果符合典型弹流问题的基本特性。

对于轮胎滑水的弹流润滑问题, 最直观的需求应是通过最小膜厚h_min来反映出临界的车速v。例如, 在汽车轮胎滑水问题中, 应尽量增大完全滑水时的临界车速, 以提高汽车行驶的安全性; 然而, 在本文试验台中, 相反地应减小完全水膜时的临界速度, 在低速下形成滑水效应, 实现润滑。

液体膜厚易受表面粗糙度等因素影响, 膜厚过小容易破裂^[9]。本文依照文献[8]中的推荐值, 最小膜厚h_min采用0.02~0.025 mm, 取0.02、0.025 mm分别分析。这里最小滑水膜厚与文献[5, 13]是有区别的, 文献中需1 mm左右水膜才能完全形成水膜润滑是针对有花纹粗糙表面的轮胎而言, 1 mm指的是路面积水厚度; 本文是针对等效的光滑胎面与水轴承面板表面之间的水膜润滑, 0.025 mm指的是形成的实际水膜厚度。积水厚度与实际水膜厚度两者概念是不同的。

当最小膜厚确定时, 可以反过来求出该最小膜厚h_min下的临界车速v。当只改变胎压p影响因素条件下, 可以一一求出对应的临界车速v(p)。

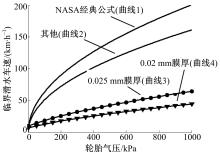
图11为临界滑水速度与轮胎胎压的关系, 其中曲线1为Horne等^[4]提出的NASA经典滑水公式u=6.34 p, 其中u为滑水车速; 曲线2为文献[14]分别通过伯努利方程、动量守恒定理推导出的同样速度的胎压曲线u= 2p/ρ, 其中ρ 为水的密度; 曲线3、4是本文分别采用0.025 mm、0.02 mm最小膜厚求出的临界速度胎压曲线。

图11

Fig.11

	Figure Option ViewDownloadNew Window
	图11 临界滑水速度与胎压关系Fig.11 Relationship between critical speed and tire pressure

对比图11中上述曲线可知:4条曲线的临界滑水速度均随胎压的增加而增大; 曲线3、4的临界滑水速度随最小水膜厚度的减小而减小, 在一定胎压下, 对应的临界车速小于曲线1(NASA滑水公式)和曲线2的临界车速。因此, 本文的轮胎台架的运行速度只要高于曲线3、4之间的某个临界速度, 便可建立起完全的水膜, 避免产生不利的摩擦磨损。

例如, 对应常见的轿车轮胎胎压220 kPa, 经典的NASA滑水速度为94 km/h; 而从图11中曲线3、4可以看出, 相对胎压220 kPa, 本台架水轴承只要速度不低于18.6~26.9 km/h时, 便可建立完全水膜, 实现了较低速度下的滑水润滑。

图12为具有水轴承系统的高速轮胎试验台实物图。

图12

Fig.12

	Figure Option ViewDownloadNew Window
	图12 具有水轴承系统的高速轮胎台Fig.12 High-speed tire test rig with water bearing

从上述分析可知, 动压滑水有最低的滑水速度, 当低于该值时, 水膜便不能完全形成。而实际工程应用中, 台架启动时难以避免低速情况, 因此在低速时应采用水轴承静压来形成水膜, 避免产生不利的摩擦磨损, 在临界速度以上时可采用动压形成水膜。