基于可靠度的冻融循环下沥青路面性能

引用本文

司伟, 马骉, 任君平, 汪海年, 格桑泽仁. 基于可靠度的冻融循环下沥青路面性能. 吉林大学学报: 工学版, 2016, 46(1): 126-132
SI Wei, MA Biao, REN Jun-ping, WANG Hai-nian, GE-Sang Ze-ren. Analysis of asphalt pavement performance under freeze-thaw cycles using reliability method. Journal of Jilin University Engineering and Technology Edition, 2016, 46(1): 126-132 复制到剪切板

Permissions

基于可靠度的冻融循环下沥青路面性能

司伟¹, 马骉¹, 任君平¹, 汪海年¹, 格桑泽仁²

1.长安大学特殊地区公路工程教育部重点实验室,西安 710064

2.西藏自治区交通厅交通科学研究所,拉萨 850000

马骉(1972-),男,教授,博士生导师.研究方向:路面结构与材料.E-mail:mb@gl.chd.edu.cn

作者简介:司伟(1986-),男,博士研究生.研究方向:路面结构与材料.E-mail:siweichd@163.com

基金:国家科技支撑计划项目(2014BAG05B04); 西部交通建设科技项目(2013318490010); 国家自然科学基金项目(51310105029)

摘要

在冻融循环试验的基础上,通过考虑影响因素的不确定性,对冻融作用下沥青路面结构的可靠性开展研究。采用冻融循环试验模拟了青藏高寒地区冻融作用对沥青混合性能的影响,建立了考虑冻融作用的路面结构强度可靠度方程,利用蒙特卡洛模拟方法对可靠度方程进行求解。研究得出:沥青混合料的抗压回弹模量在冻融作用下呈衰减趋势,初始冻融作用下混合料性能衰减较快,经历8~10次冻融循环后性能衰减趋于平缓;路面结构承载能力(可靠度)随冻融作用次数的增加呈衰减趋势,冻融作用对路面结构的可靠度有显著影响;路面结构可靠度随冻融循环变异系数的增加呈降低趋势。本文提出的考虑冻融作用的沥青路面可靠度分析方法可以较好地反映寒冷地区冻融作用对路面性能的影响。

关键词: 道路工程; 冻融循环; 可靠度分析; 蒙特卡洛模拟; 沥青混合料

中图分类号:U416 文献标志码:A 文章编号:1671-5497(2016)01-0126-07

Analysis of asphalt pavement performance under freeze-thaw cycles using reliability method

SI Wei¹, MA Biao¹, REN Jun-ping¹, WANG Hai-nian¹, GE-Sang Ze-ren²

1.Key Laboratory of Special Area Highway Engineering of Ministry of Education, Chang'an University, Xi'an 710064, China

2.Institute of Traffic Science,Traffic Bureau of Tibet,Lhasa 850000,China

Abstract

The reliability of the pavement structure under Freeze-Thaw (F-T) cycles is studied based on simulation test, in which various uncertainties of influence factors are taken into account. The impact of F-T cycles in Qinghai-Tibet cold region is simulated by F-T cycle test, and the reliability function of the asphalt pavement structure is built. Monte Carlo simulation method is employed to solve the reliability function. Analytical results show that the resilient modulus of asphalt concrete mixture declines under F-T cycles, the mixture performance decreases sharply in the initial F-T cycles and turns to gentle after 8 to 10 F-T cycles. The F-T cycle has significant impact on the reliability of the pavement structure, which decreases as F-T cycles increase. The reliability of the pavement structure also decreases as the coefficient of variance increases. An analysis method of the reliability of pavement structure under F-T cycles is proposed, which is useful to reflect the actual impact of F-T cycles on pavement performance in cold region.

Keyword: road engineering; freeze thaw cycles; reliability analysis; Monte Carlo simulation; asphalt mixture

Show Figures

0 引言

所有的基础设施工程都面临由于性能衰减、衰退而导致其失效的难题^{[1, 2]}。已有研究表明, 在特殊地区(多年冻土区、湿陷性黄土地区、沙漠地区等)外界环境对道路性能的影响甚至要大于行车荷载作用^{[3, 4, 5]}。沥青是温度敏感性材料, 沥青混合料性能随温度的影响较大。温度和水分是影响沥青路面性能最主要的两个气候环境因素^{[3, 4, 5, 6]}。青藏高寒区年平均气温低、温差大、降温速率快, 冻融循环频繁、剧烈, 多种不利条件对沥青混合料的力学性能、耐久性等有明显影响; 沥青路面病害与面层沥青混合料在特殊条件下的性能衰变相关^[7]。低温开裂与温度疲劳裂缝是寒冷地区沥青路面温度裂缝的两种主要形式^[3]。在快速降温或持续低温条件下, 沥青路面产生温度应力; 当温度应力超过混合料的抗拉强度时出现低温开裂; 当温度应力小于混合料的抗拉强度时, 混合料表面无明显裂缝, 而其内部将产生细微裂缝并逐渐积累, 随着温度应力的反复作用最终导致混合料产生温度疲劳裂缝, 并诱发其他病害^{[5, 6]}。沥青路面在降水或潮湿环境中, 在行驶车轮作用下将产生动水压力及真空负压抽吸作用, 导致沥青面层混合料剥落、孔隙变大, 从而加速道路性能与承载能力的衰减^{[5, 6, 7]}。

众多学者关于温度与水分对寒冷地区沥青路面性能的影响开展了探索研究, 然而由于试验条件、试验方法、评价模型、数值模拟等多方面因素的差异, 至今仍没有统一可行的评价方法与指标。利用冻融循环试验方法模拟温度与水分对沥青混合料性能的影响。该方法虽然模拟了温度与水分对混合料性能的影响, 但这仅得到了混合料性能的变化趋势, 而没有将沥青路面性能变化以及沥青路面相关设计指标结合起来, 不能宏观反映外界因素对沥青路面性能的影响。而现有研究关于道路性能的衰减模型大多只考虑了行车荷载作用, 忽视了外界气候环境的影响; 有少数道路性能衰减模型虽然考虑了外界气候环境的影响, 但将其作用视为固定值, 没有考虑外界环境变化的不确定性, 使研究结果与实际有较大的偏离。为此, 本文利用可靠度分析方法^{[8, 9]}, 通过AASHTO设计方程, 引入影响参数的不确定性, 分析冻融循环作用对道路性能的影响。

本文研究的目的在于利用冻融循环试验分析沥青混合料回弹模量在冻融循环作用下的变化, 并利用可靠度模型分析回弹模量在冻融条件下的衰减对道路承载能力的影响; 在可靠度模型中考虑了参数变化的不确定性。本文研究结果为完善寒冷地区沥青路面设计参数取值提供依据。

1 试验材料与可靠度分析方法

1.1 试验原材料与冻融循环试验

本试验采用青藏高原地区常用的SBR成品改性沥青, 其性能技术指标如表1所示。集料取自青藏公路沿线料场, 以石灰岩为主, 矿粉为石灰岩矿粉。

表1 沥青技术指标试验结果 Table 1 Test results of asphalt parameters

试验沥青混合料为AC-13, 级配组成采用《公路沥青路面设计规范》(JTG D50-2006)推荐中值。在标准马歇尔试验的基础上, 兼顾西藏地区特殊的气候条件与交通状况, 确定了SBR改性AC-13沥青混合料的最佳油石比为5.5%。

关于沥青混合料冻融循环试验, 本文在参考国内相关冻融循环试验条件^{[4, 5, 6, 7]}的基础上, 依据青藏公路实际条件自行制定试验方法。青藏公路沿线气象资料表明, 年平均最低气温为-14.5 ℃~-17.4 ℃, 年平均最高气温为6.8 ℃~8.1 ℃; 5~8月的气温达到正温; 昼夜温差可达23 ℃~26 ℃^[10]。为此, 本文提出的冻融循环试验, 冻结时利用塑料袋将试件密封, 并在塑料袋中注水30 mL, 冻结温度为(-25± 1) ℃, 冻结时间12 h; 融化时将试件直接放入恒温水浴, 融化温度为(25± 1) ℃, 融化时间为12 h; 利用低温冷冻箱与恒温水浴模拟冻融作用。采用静压法成型混合料试件, 利用电子万能试验机试验, 计算机自动采集数据, 温度控制装置为环境箱, 温控精度为± 0.1 ℃, 试验温度为15 ℃, 加载速率为2 mm/min。

1.2 可靠度理论

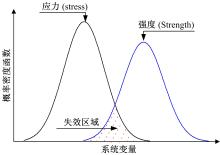
应力-强度模型(Stress-strength model, 或Demand-supply model)是可靠度分析中最常见的模型, 该模型通过比较被定义为随机变量的应力(或荷载)与强度评价其系统的可靠度; 当应力水平超过其强度水平时, 说明该系统失效^{[1, 11, 12]}。图1为典型的应力-强度模型示意图, 可以看出可靠度失效发生在应力与强度的重叠区域, 该区域面积与其失效概率成正比。

	Figure Option View Download New Window
	图1 失效区域概率Fig.1 Probability of failure region

在可靠度分析中, 可靠度方程可以分解为应力方程和强度方程, 而这两个方程往往为两个不同的研究对象。结构可靠度模型是由n个基本的随机变量X=[x₁, x₂, …, x_n]^T, 以及一个约束方程G(x)组成, 约束方程如式(1)所示:

$\begin{matrix} G (x) = Strengt h - stress (1) \end{matrix}$

式中:stress和Strength分别代表应力方程和强度方程。

对于定义的约束方程, 结构的失效状态可以表示为{G(x)≤ 0}, 失效概率可以表示为n维的概率积分方程, 如式(2)所示:

pF=prob[G(x)≤ 0]=∫ _G₍_x_{)≤ 0}f(x)dX(2)

式中:f(x)是随机变量X的联合概率密度函数。

利用约束方程可以计算结构的失效概率以及可靠度指数β 。Ang等提出了利用约束方程的均值E_{Strength-stress}和方差σ _{Strength-stress}计算其相关可靠度的方法^[13]。均值为:

$\begin{matrix} E_{Strengt h - stress} = E (Strengt h) - E (stress) \end{matrix}$

方差为:

$\begin{matrix} σ_{Strengt h - stress} = \sqrt[]{σ_{Strengt h}^{2} + σ_{stress}^{2}} \end{matrix}$

其中E(Strength)和E(stress)分别为Strength和stress的期望, $\begin{matrix} σ_{Streng t h}^{2} \end{matrix}$ 和 $\begin{matrix} σ_{stress}^{2} \end{matrix}$ 分别为Strength和stress的方差。从而, 其可靠度指数β 可以表示为:

$\begin{matrix} β = \frac{E_{Strengt h} - E_{stress}}{\sqrt[]{σ_{Strengt h}^{2} + σ_{stress}^{2}}} (3) \end{matrix}$

失效区域的概率是工程系统在其期望条件下运行而失效的估计值。因此, 可靠度的失效区域的概率如下所示:

$\begin{matrix} pF = prob [G (x) \leq 0] = Φ (- β) (4) \end{matrix}$

式中:Φ 为标准正态方程的分布函数, 失效发生在应力与强度分布的重叠区域, 失效区域面积与失效概率成正比。

1.3 AASHTO设计方程

AASHTO设计方法是世界范围内影响最大也是应用最广的沥青路面设计方法, 该方法根据AASHTO试验路的数据而建立。当不考虑参数的变异时, 可靠度分析中路面结构的强度方程可以由AASHTO设计方程表示^[14]。

$\begin{matrix} \begin{matrix} \log W_{18} = 9.36 \log (SN + 1) - 0.20 + \\ \frac{\log [ΔPSI / (4.2 - 1.5)]}{0.4 + 1094 / {(SN + 1)}^{5.19}} + \\ 2.32 \log M_{r} - 8.07 (5) \end{matrix} \end{matrix}$

式中:W₁₈是允许的荷载作用次数, 它等价为80 kN的单轴当量荷载ESAL; Δ PSI是现时服务能力指数的减小值; SN是结构层系数; M_r是有效的路基回弹模量。

结构层系数由式(6)计算^[14]。

$\begin{matrix} SN = a_{1} D_{1} + a_{2} D_{2} m_{2} + a_{3} D_{3} m_{3} (6) \end{matrix}$

式中:a₁、a₂和a₃分别为沥青面层系数、基层系数和底基层系数; D₁、D₂和D₃为对应的结构层厚度; m₂和m₃分别为基层和底基层的排水系数。

2 试验结果与分析

2.1 冻融循环对抗压回弹模量的影响

AC-13沥青混合料经历14次冻融循环试验后, 其抗压回弹模量如图2所示。

	Figure Option View Download New Window
	图2 冻融循环作用对抗压回弹模量的影响Fig.2 Impact of freeze-thaw cycles on resilient modulus

由图2可见, 沥青混合料的抗压回弹模量随冻融循环次数的增加呈减小趋势。初期冻融循环作用下混合料的抗压回弹模量下降明显, 经历约4次冻融循环作用后, 混合料的抗压回弹模量衰减趋势逐渐减小; 在8~10次冻融循环后, 沥青混合料抗压回弹模量衰减趋势逐渐趋于平缓。经历14次冻融循环后, 抗压回弹模量减小了152 MPa, 与未冻融相比抗压回弹模量降低了19.3%。

沥青混合料抗压回弹模量是表征强度和变形的函数, 混合料受压破坏时, 压缩变形由可压缩的空隙(和孔隙)空气和混合料整体变形共同构成。成型的沥青混合料内部存在一定的闭口空隙和开口空隙, 在饱水冻融循环作用下, 开口空隙充满自由水分, 水结冰后体积增大, 产生膨胀力^{[4, 5, 15, 16, 17]}。在反复冻融循环作用下, 孔隙壁承受冻胀压力和渗透压力, 使沥青与集料的粘结力持续衰减, 结构将变得松散, 导致孔隙壁受损开裂^{[4, 5, 15, 16, 17]}。开口空隙增大后将与部分闭口空隙连通, 增大了开口空隙的比例, 从而进一步扩大了混合料的内部损伤。混合料的抗压回弹模量除了与沥青和细集料的变形有关外, 与粗集料骨架的变形也有一定的关系。反复冻融循环作用后, 混合料空隙被撑大, 影响粗集料的相互嵌挤, 混合料在压缩破坏时骨架变形增大^{[4, 7, 17]}。冻水渗透压力破坏了集料表面的结构沥青, 使集料间的粘结力下降, 减小了结构沥青对整个粗集料骨架的粘结作用。因此, 当混合料经历冻融循环作用后, 其抗压回弹模量呈减小趋势。

如图2所示, 混合料抗压回弹模量随冻融循环次数近似呈指数形式变化。为此, 本文利用非线性指数模型对抗压回弹模量进行分析, 指数模型如下所示^{[18, 19]}:

$\begin{matrix} y = a + b e^{e \times x} + ε, ε ~ N (0, δ^{2}) (7) \end{matrix}$

式中:y为因变量, 代表抗压回弹模量; a为参数, 代表抗压回弹模量的初始值; b为参数, 代表性能衰减的速率; c为参数, 代表方程的曲率; x为解释变量, 代表冻融循环次数; ε 为误差项。

模型中假设随机变量ε 的均值为零, 方差具有齐次性并与因变量不相关, 服从正态分布。参数估计采用最小二乘法, 由于ε 的正态分布性, 可以利用χ ²值评价拟合参数的有效性^{[18, 19]}。

指数模型关于抗压回弹模量的拟合结果如表2所示。结果表明, 指数模型较好的反映了抗压回弹模量与冻融循环次数的关系, $\begin{matrix} R_{adj}^{2} \end{matrix}$ 为0.88。方差分析结果表明, 试验数据与指数模型在0.01显著性水平下是统计显著的, 即两者具有很好的相关性。

表2 指数模型拟合结果 Table 2 Fitting results of exponential model

	a		b		c	减小的 χ ²	$\begin{matrix} R_{adj}^{2} \end{matrix}$
	数值		标准误差		数值	减小的 χ ²	$\begin{matrix} R_{adj}^{2} \end{matrix}$	标准误差	数值	标准误差
回弹模量	625.33	23.80		151.92	25.58		-0.21	0.11	366.67	0.88

表2 指数模型拟合结果 Table 2 Fitting results of exponential model

2.2 结构层系数计算

由于混合料的抗压回弹模量随冻融循环次数的增加而减小, 导致路面结构的承载能力降低。已有研究表明^{[3, 20]}, 结构层系数SN可以很好地反映路面结构的承载能力。如式(6)中, 各层系数a_i、结构层厚度D_i、排水系数m_i共同决定了结构层系数的变化, 而本文只考虑冻融循环作用对沥青面层系数a₁有影响, 假定其他参数不受冻融作用影响, 从而通过沥青面层系数a₁的变化研究冻融作用对路面结构承载能力的影响。

各层的层系数a_i是沥青路面结构中表征材料性能的参数。根据AASHTO指南^[14], 材料的回弹模量是决定该层系数的主要参数。通过室外试验得到的经验方程可以求解不同材料的层系数。普遍应用的沥青面层系数计算经验方程如下^[20]:

$\begin{matrix} \begin{matrix} a_{1} = 0.4 \times \log (\frac{E}{3000}) + 0.44 (8) \\ 0.20 < a_{1} < 0.44 \end{matrix} \end{matrix}$

式中:a₁为沥青面层系数; E为沥青面层混合料抗压回弹模量, 单位为MPa, 本文为冻融循环作用后的抗压回弹模量。

利用式(8)得到冻融后沥青面层系数a₁₍_F-T₎后, 将其代入式(6)可以求得冻融后结构层系数SN_F-T。由于抗压回弹模量在冻融循环作用下呈现出不确定性, 在可靠度分析中结构层系数SN_F-T取与抗压回弹模量相同的不确定性。

2.3 关于AASHTO设计方法的可靠度方程

在路面结构承载能力可靠度分析中, 应力分析主要针对交通量的预测; 而强度分析主要处理关于路面结构强度的材料性能与结构设计^[21]。可靠度模型中, 应力方程可以用相应时间段内累积的当量单轴(80 kN)荷载方程表示。美国沥青协会与AASHTO设计方法推荐利用交通增长率来获得在整个设计期内的交通量, 计算公式如下^{[3, 14]}:

$\begin{matrix} N (t) = ESA L_{0} \times TGF = ESA L_{0} \times \frac{(1 + r)' - 1}{r} (9) \end{matrix}$

式中:N(t)为t年内总交通量; ESAL₀为初始交通量; TGF为总增长率; r为年交通增长率; t为设计年限。

由强度方程(5)和应力方程(9)可以得到相应的约束方程, 如式(10)所示:

$\begin{matrix} \begin{matrix} G (S N_{F - T}, ΔPSI, M_{r}, ESA L_{0}, r, t) = \\ \log W_{18} - logN (t) (10) \end{matrix} \end{matrix}$

基于约束方程(10), 可靠度失效区域可以表示为{G(SN_F-T, Δ PSI, M_r, ESAL₀, r, t)≤ 0}, 其相应的概率积分方程如下:

$\begin{matrix} \begin{matrix} F (t) = \int_{G}^{(} f (S N_{F - T}, ΔPSI, \\ M_{r}, ESA L_{0}, r, t) \times dS N_{F - T} dΔPSId M_{r} dESA L_{0} dr (11) \end{matrix} \end{matrix}$

式(11)中积分极为复杂, 用常规方法很难直接计算。多种近似求解方法被提出用来解决此类积分问题, 运用最为普遍的方法有蒙特卡洛模拟(Monte Carlo simulation)与一次二阶矩法(First order reliability method), 以及后来发展起来的二次二阶矩法(Second order reliability method)^{[1, 9, 12, 21]}。一次二阶矩法是基于非线性约束方程在设计点处的线性估计方法, 一般用泰勒级数展开使之线性化; 然而该方法对高度非线性的约束方程估计精度较差, 并很难在迭代过程中找到设计点。一次二阶矩法的不足可以利用二次二阶矩法进行一定的弥补。Zhang等^[1]基于AASHTO设计方法, 利用高阶计算方法对路面结构的可靠度进行了分析。蒙特卡洛模拟是依赖于随机抽样的计算方法, 随着计算机技术与编程技术的发展, 计算过程复杂与计算量大的问题得到了很好的解决, 与其他方法相比, 此方法可以应用于解决大多数难题, 其计算精度随样本空间的增大而增大。为此, 本文选用蒙特卡洛模拟求解约束方程并计算其可靠度。

除了沥青面层的回弹模量外, 其他路面参数取值均采用Huang的推荐值^[3]。沥青面层厚度为203 mm、基层厚度为178 mm、底基层厚度为292 mm; 基层与底基层回弹模量分别为207和76 MPa; 路基有效回弹模量为39.3 MPa; 减少的现时服务能力指数Δ PSI为2; 基层和底基层的排水系数为1.2; 基层系数和底基层系数分别为0.14和0.08。

2.4 可靠度分析

为了分析冻融循环作用对路面结构承载能力的影响, 本文给出设计年限内预计的累计当量单轴荷载ESAL为5 000 000, 设计年限为50年。约束方程中的这些基本随机变量都假设为相互独立并呈正态分布。4个基本随机变量为年当量单轴荷载ESAL₀、底基层回弹模量M_r、年交通增长率r和冻融循环下结构层系数SN_F-T, 前3个的均值分别为109 261、5700和0.05; 冻融循环下结构层系数随冻融循环作用而变化。4个基本变量的变异系数CV分别为10%、15%、10%和10%^[3]。为了比较冻融循环作用下结构层系数变化的不确定性对路面结构承载能力的影响, 本文将进行其敏感性分析。冻融循环作用下结构层系数的变异系数取5%、10%、15%和20%。由于大样本可以提高蒙特卡洛模拟的精度, 为此本文模拟时样本个数取1 000 000个。

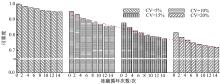
图3反映了第十年路面结构的可靠度与冻融循环作用在不同变异系数下的变化关系。对于不同变异系数下的冻融循环, 可靠度均随冻融循环次数的增加而减小。在相同冻融条件下, 可靠度随变异系数的增大而减小。经历14次冻融循环后, 变异系数为5%时可靠度减小了4.7%, 与未冻融相比减小了4.73%; 变异系数为15%时可靠度减小了10.3%, 与未冻融相比减小了11.7%。对比变异系数为5%和15%时的可靠度, 在未冻融作用下两者的差异为11.8%; 经历14次冻融循环作用后, 两者的差异为17.4%。结果表明, 冻融循环作用的不确定性对路面结构可靠度有显著的影响, 变异系数越大其影响越显著。

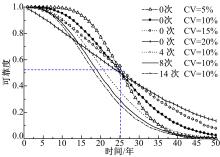
	Figure Option View Download New Window
	图3 冻融循环对可靠度的影响Fig.3 Impact of freeze-thaw cycles on reliability

图4为路面结构可靠度在不同冻融循环作用以及变异系数下随使用年限的衰减趋势。图4中, 路面结构可靠度随使用年限的增加呈降低趋势, 从第10年开始可靠度降低速率明显增大, 直到第30年其降低速率才趋于平缓。说明第10~30年是可靠度下降的主要区间, 在该区间内应对道路采取有效的养护措施, 制止道路持续恶化, 从而提高可靠度, 延长其使用寿命。对于具有相同变异系数(CV=10%)的可靠度, 从图中可以看出在整个使用年限内可靠度变化趋势一致, 说明冻融循环作用不会改变可靠度的变化趋势, 只影响其变化的幅度。

	Figure Option View Download New Window
	图4 可靠度方程中关于冻融循环作用的敏感性分析Fig.4 Sensitivity of reliability function of F-T cycles

对于未遭受冻融循环作用的可靠度, 随着变异系数的变化其可靠度变化也略有所不同, 在接近25年时曲线出现交叉点。在前25年, 变异系数越小, 其可靠度越大; 当超过25年后, 可靠度呈相反变化, 这说明当变异系数越大时, 其不确定性越大, 从而为道路性能的预估带来更大的困扰, 也为道路的运营管理带来困难。对于不同变异系数情形下的可靠度, 第25年是其可靠度变化的转折点, 说明在该点以前要尽可能地降低外界影响的变异系数。结果分析表明, 降低冻融循环作用引起的不确定性可以有效增加路面结构承载能力的可靠度。

实际上, 冻融循环作用对路面结构造成的影响远不止沥青混合料的回弹模量, 对其他材料性能都会产生负面影响。本文只以沥青混合料的回弹模量为例, 说明了冻融作用对路面结构的危害。从以上分析结果可知, 冻融循环作用对路面结构的影响极其显著, 因而在实际工程中不应忽略这一外界因素。

3 结论

(1)沥青混合料抗压回弹模量随冻融循环次数的增加呈降低趋势, 初期抗压回弹模量衰减较快, 经历8~10次冻融循环后性能衰减趋于平缓; 利用指数模型可以较好地反映抗压回弹模量随冻融循环次数的变化, 在0.01水平下该模型是统计性显著的。

(2)利用AASHTO设计方法与设计年限内交通量可以建立关于沥青路面结构承载能力的可靠度方程, 可通过结构层系数的变化来反映冻融循环作用的不确定性。

(3)路面结构的可靠度随冻融循环作用的增加呈减小趋势, 变化程度随变异系数的增大而增大; 敏感性分析表明冻融循环作用与其变异系数对路面结构的承载能力有显著的影响, 降低冻融循环作用的变异系数可以有效增加路面结构的可靠度。

(4)本文只以冻融循环对沥青混合料抗压回弹模量的作用为例, 分析了冻融作用对路面结构承载能力可靠度的影响, 这与实际作用还有较大差异, 后期研究应考虑更多的影响因素。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Zhang Zhan-min, Ivan Damnjanovi C. Applying method of moments to model reliability of pavements infrastructure[J]. Journal of Transportation Engineering, 2006, 132(5): 416-424. [本文引用:4]
[2]	Hong F, Prozzi J A. Estimation of pavement performance deterioration using Bayesian approach[J]. Journal of Infrastructure Systems, 2006, 12(2): 77-86. [本文引用:1]
[3]	Huang Y H. Pavement Analysis and Design[M]. 2nd ed. New Jersey: Prentice-Hall, 2004. [本文引用:7]
[4]	司伟, 马骉, 汪海年, 等. 高原寒冷地区沥青混合料冻融循环作用下弯拉特性分析[J]. 吉林大学学报: 工学版, 2013, 43(4): 885-890. Si Wei, Ma Biao, Wang Hai-nian, et al. Analysis on compression characteristics of asphalt mixture under freeze-thaw cycles in cold plateau regions[J]. Journal of Jilin University(Engineering and Technology Edition), 2013, 43(4): 885-890. [本文引用:6]
[5]	Feng D, Yi J, Wang D, et al. Impact of salt and freeze-thaw cycles on performance of asphalt mixtures in coastal frozen region of China[J]. Cold Regions Science and Technology, 2010, 62(1): 34-41. [本文引用:7]
[6]	Kettil P, Engström G, Wiberg N E. Coupled hydro-mechanical wave propagation in road structures[J]. Computers and Structures, 2005, 83(21): 1719-1729. [本文引用:4]
[7]	马骉, 韦佑坡, 王磊, 等. 高原寒冷地区沥青混合料弯拉特性分析[J]. 公路交通科技, 2010, 27(3): 44-48. Ma Biao, Wei You-po, Wang Lei, et al. Analysis on flexural tensile characteristics of asphalt mixture in cold plateau region[J]. Journal of Highway and Transportation Research and Development, 2010, 27(3): 44-48. [本文引用:4]
[8]	Alsherri A, George K P. Reliability model for pavement performance[J]. Journal of Transportation Engineering, 1988, 114(3): 294-306. [本文引用:1]
[9]	Roberts E M. Structural Reliability Analysis and Prediction[M]. 2nd ed. West Sussex, England : John Wiley & Sons, 1999. [本文引用:2]
[10]	国家气象局数据中心. 五道梁、沱沱河、安多地区地面气象资料三十年数据汇编[Z]. 北京: 国家气象局数据中心, 2003. [本文引用:1]
[11]	Sundararajan C. Probabilistic Structural Mechanics Hand book[M]. New York: Chapman & Hall, 1995. [本文引用:1]
[12]	Ditlevsen O, Madsen H O. Structural Reliability Methods[M]. Chichester: Wiley, 1996. [本文引用:2]
[13]	Ang A H S, Tang W H. Probability Concepts in Engineering: Emphasis on Applications to Civil and Environmental Engineering[M]. 2nd ed. New York: Wiley, 2007. [本文引用:1]
[14]	AASHTO. Resistance of compacted asphalt mixtures to moisture-induced damage[S]. Washington D C: AASHTO, 1991. [本文引用:4]
[15]	Goh S, Akin M, You Z, et al. Effect of deicing solutions on the tensile strength of micro- or nano-modified asphalt mixture[J]. Construction and Building Materials, 2011, 25(1): 195-200. [本文引用:2]
[16]	M'hammed Merbouh. Effect of thermal cycling on the creep-recovery behaviour of road bitumen[J]. Energy Procedia, 2012, 18: 1106-1114. [本文引用:2]
[17]	侯曙光, 李志栋, 黄晓明, 等. 利用冻融飞散试验进行沥青混合料抗冻性能评价[J]. 公路交通科技, 2006(2): 7-10. Hou Shu-guang, Li Zhi-dong, Huang Xiao-ming, et al. Asphalt mixture antifreeze capability evaluation using freezing-thawing and scattering loss test[J]. Journal of Highway and Transportation Research and Development, 2006(2): 7-10. [本文引用:3]
[18]	Washington S P, Karlaftis M G, Mannering F L. Statistical and Economic Methods for Transportation Data Analysis[M]. New York: Chapman & Hall, 2011. [本文引用:2]
[19]	Greene W. Econometric Analysis[M]. 5th ed. Upper Saddle River: Prentice-Hall, 2002. [本文引用:2]
[20]	Hussain U, Bahia Bosscher P J, Christensen J, et al. Layer coefficients for new and reprocessed asphaltic mixes. No. WI/SPR-04-00[R]. Wisconsin Dept. of Transportation, Division of Transportation Infrastructure Development, Bureau of Highway Construction, Technology Advancement Unit, 2000. [本文引用:2]
[21]	Vighnesh P Deshpand e, Damnjanovic Ivan D, Gardoni Paolo. Modeling pavement fragility[J]. Journal of Transportation Engineering, 2009, 136(6): 592-596. [本文引用:2]

2006

0.0

... 0 引言所有的基础设施工程都面临由于性能衰减、衰退而导致其失效的难题^[1,2] ...

... 当应力水平超过其强度水平时,说明该系统失效^[1,11,12] ...

... 多种近似求解方法被提出用来解决此类积分问题,运用最为普遍的方法有蒙特卡洛模拟(Monte Carlo simulation)与一次二阶矩法(First order reliability method),以及后来发展起来的二次二阶矩法(Second order reliability method)^[1,9,12,21] ...

... Zhang等^[1]基于AASHTO设计方法,利用高阶计算方法对路面结构的可靠度进行了分析 ...

2006

0.0

... 0 引言所有的基础设施工程都面临由于性能衰减、衰退而导致其失效的难题^[1,2] ...

2004

0.0

... 已有研究表明,在特殊地区(多年冻土区、湿陷性黄土地区、沙漠地区等)外界环境对道路性能的影响甚至要大于行车荷载作用^[3,4,5] ...

... 温度和水分是影响沥青路面性能最主要的两个气候环境因素^[3,4,5,6] ...

... 低温开裂与温度疲劳裂缝是寒冷地区沥青路面温度裂缝的两种主要形式^[3] ...

... 已有研究表明^[3,20],结构层系数SN可以很好地反映路面结构的承载能力 ...

... 美国沥青协会与AASHTO设计方法推荐利用交通增长率来获得在整个设计期内的交通量,计算公式如下^[3,14]: ...

... 除了沥青面层的回弹模量外,其他路面参数取值均采用Huang的推荐值^[3] ...

... 4个基本变量的变异系数CV分别为10%、15%、10%和10%^[3] ...

2013

0.0

. 2013, 43(4):885-890 DOI:10.7964/jdxbgxb201304007

Analysis on compression characteristics of asphalt mixture under freeze-thaw cycles in cold plateau regions

高原寒冷地区沥青混合料冻融循环作用下弯拉特性分析

Si Wei , Ma Biao , Wang Hai-nian

司伟, 马骉, 汪海年

1. Key Laboratory of Special Area Highway Engineering of Ministry of Education, Highway School, Chang'an University, Xi'an 710064, China; 2. Technology and Science Center, The Second Highway Engineering of China Communications Construction Company Ltd., Xi'an 710065, China

By bending test of asphalt mixture under freeze-thaw conditions,the influences of freeze-thaw cycles,asphalt-aggregate ratio and gradation composition on the flexural characteristics of asphalt mixture were investigated.Experiment results show that,the flexural tensile strength, the flexural-tensile strain and the stiffness modulus of asphalt mixture decrease with the increase in the number of freeze-thaw cycles. Obvious influences of the asphalt-aggregate ratio and gradation composition on the flexural characteristics were observed.As the asphalt- aggregate ratio increases, the influence of freeze-thaw cycles on the flexural characteristics decreases.The flexural characteristics of AC-13 mixture are better than that of other two gradations.It is shown that applying AC-13 mixture with 5.5% OAC or higher can improve low temperature flexural characteristics of the asphalt mixture under freeze-thaw cycle condition.

通过沥青混合料在冻融循环作用下的弯曲试验,分析了冻融循环次数、油石比、级配组成对混合料弯拉特性的影响。试验结果表明:随着冻融循环次数的增多,沥青混合料的弯拉强度、弯拉应变、劲度模量均呈减小趋势。油石比、级配组成对弯拉特性有明显影响,随着油石比的增大,冻融循环作用对沥青混合料弯拉特性的影响减小,AC-13混合料的弯拉特性优于其他两种级配。在青藏高原寒冷地区采用AC-13的沥青混合料、油石比为5.5%或适当增加油石比可以提高沥青混合料在冻融循环作用下的低温弯曲特性。

... 已有研究表明,在特殊地区(多年冻土区、湿陷性黄土地区、沙漠地区等)外界环境对道路性能的影响甚至要大于行车荷载作用^[3,4,5] ...

... 温度和水分是影响沥青路面性能最主要的两个气候环境因素^[3,4,5,6] ...

... 关于沥青混合料冻融循环试验,本文在参考国内相关冻融循环试验条件^[4,5,6,7]的基础上,依据青藏公路实际条件自行制定试验方法 ...

... 成型的沥青混合料内部存在一定的闭口空隙和开口空隙,在饱水冻融循环作用下,开口空隙充满自由水分,水结冰后体积增大,产生膨胀力^{[4,5,15,16,17]} ...

... 在反复冻融循环作用下,孔隙壁承受冻胀压力和渗透压力,使沥青与集料的粘结力持续衰减,结构将变得松散,导致孔隙壁受损开裂^{[4,5,15,16,17]} ...

... 反复冻融循环作用后,混合料空隙被撑大,影响粗集料的相互嵌挤,混合料在压缩破坏时骨架变形增大^[4,7,17] ...

2010

0.0

... 已有研究表明,在特殊地区(多年冻土区、湿陷性黄土地区、沙漠地区等)外界环境对道路性能的影响甚至要大于行车荷载作用^[3,4,5] ...

... 温度和水分是影响沥青路面性能最主要的两个气候环境因素^[3,4,5,6] ...

... 当温度应力小于混合料的抗拉强度时,混合料表面无明显裂缝,而其内部将产生细微裂缝并逐渐积累,随着温度应力的反复作用最终导致混合料产生温度疲劳裂缝,并诱发其他病害^[5,6] ...

... 沥青路面在降水或潮湿环境中,在行驶车轮作用下将产生动水压力及真空负压抽吸作用,导致沥青面层混合料剥落、孔隙变大,从而加速道路性能与承载能力的衰减^[5,6,7] ...

... 关于沥青混合料冻融循环试验,本文在参考国内相关冻融循环试验条件^[4,5,6,7]的基础上,依据青藏公路实际条件自行制定试验方法 ...

... 成型的沥青混合料内部存在一定的闭口空隙和开口空隙,在饱水冻融循环作用下,开口空隙充满自由水分,水结冰后体积增大,产生膨胀力^{[4,5,15,16,17]} ...

... 在反复冻融循环作用下,孔隙壁承受冻胀压力和渗透压力,使沥青与集料的粘结力持续衰减,结构将变得松散,导致孔隙壁受损开裂^{[4,5,15,16,17]} ...

2005

0.0

... 温度和水分是影响沥青路面性能最主要的两个气候环境因素^[3,4,5,6] ...

... 关于沥青混合料冻融循环试验,本文在参考国内相关冻融循环试验条件^[4,5,6,7]的基础上,依据青藏公路实际条件自行制定试验方法 ...

2010

0.0

. 2010, 27(3):44-48

Analysis on flexural tensile characteristics of asphalt mixture in cold plateau region

高原寒冷地区沥青混合料弯拉特性分析

Ma Biao , Wei You-po , Wang Lei

马骉, 韦佑坡, 王磊

1. Key Laboratory for Special Area Highway Engineering of Ministry of Education,Chang'an University,Xi'an Shaanxi 710064,China; 2. Engineering Design & Research Institute of Chang'an University,Xi'an Shaanxi 710064,China; 3. Shaanxi Provincial Communications Construction Group,Xi'an Shaanxi 710075,China

Aimed at the climate feature of low temperature and large temperature difference in Qinghai-Tibet plateau area,effects of temperature,asphalt types,asphalt-aggregate ratio,aggregate gradation on the flexural tensile characteristics of asphalt mixture were analyzed by flexuml testing.The test results show that(1)Changing of the flexural tensile strength of asphalt mixture is a convex curve in shape,the stiffness modulus of asphalt mixture reduces with increasing of the flexure tensile strain;(2) The flexural tensile strength and the flexuml tensile strain of modified asphalt and hish grade asphalt mixture are comparatively large,while the flexure tensile stiffness modulus less;(3)With increasing of asphalt-aggregate ratio,the flexural tensile strength linearly increases at first and decreases afterwards,the flexure tensile strain increases and the stiffness modulus decreases;(4)The flexural tensile strength of the asphalt mixture increases when the aggregate gradation becomes coarse.The results indicate that temperature evidently effects on the flexural tensile characteristics of asphalt mixture.The low temperature flexural tensile characteristics of asphalt mixture can be enhanced by adopting modified asphalt and hish grade asphalt,increasing asphalt-aggregate ratio and adopting coarse gradation.

针对青藏高原寒冷地区低温、大温差气候特点,通过沥青混合料弯曲试验,分析了温度、沥青种类、油石比、级配等对混合料弯拉特性的影响。试验得出,沥青混合料弯拉强度随着温度的升高呈上凸抛物线形变化,弯拉应变逐渐增大,劲度模量不断减小;改性沥青和高标号沥青混合料的弯拉强度和弯拉应变较大,劲度模量较小;油石比增加时,沥青混合料弯拉强度先线性增大后减小,弯拉应变增大,劲度模量减小;矿料级配越粗,沥青混合料弯拉强度越大。结果表明,温度对沥青混合料弯拉特性的影响较大,采用改性和高标号沥青,适当增加油石比、采用较粗矿料级配,有利于提高沥青混合料的低温弯曲性能。

... 沥青路面病害与面层沥青混合料在特殊条件下的性能衰变相关^[7] ...

... 关于沥青混合料冻融循环试验,本文在参考国内相关冻融循环试验条件^[4,5,6,7]的基础上,依据青藏公路实际条件自行制定试验方法 ...

... 反复冻融循环作用后,混合料空隙被撑大,影响粗集料的相互嵌挤,混合料在压缩破坏时骨架变形增大^[4,7,17] ...

1988

0.0

... 为此,本文利用可靠度分析方法^[8,9],通过AASHTO设计方程,引入影响参数的不确定性,分析冻融循环作用对道路性能的影响 ...

1999

0.0

... 为此,本文利用可靠度分析方法^[8,9],通过AASHTO设计方程,引入影响参数的不确定性,分析冻融循环作用对道路性能的影响 ...

2003

0.0

... 昼夜温差可达23 ℃~26 ℃^[10] ...

1995

0.0

... 当应力水平超过其强度水平时,说明该系统失效^[1,11,12] ...

1996

0.0

... 当应力水平超过其强度水平时,说明该系统失效^[1,11,12] ...

2007

0.0

... _{Strength-stress}计算其相关可靠度的方法^[13] ...

1991

0.0

... 当不考虑参数的变异时,可靠度分析中路面结构的强度方程可以由AASHTO设计方程表示^[14] ...

... 结构层系数由式(6)计算^[14] ...

... 根据AASHTO指南^[14],材料的回弹模量是决定该层系数的主要参数 ...

... 美国沥青协会与AASHTO设计方法推荐利用交通增长率来获得在整个设计期内的交通量,计算公式如下^[3,14]: ...

2011

0.0

... 成型的沥青混合料内部存在一定的闭口空隙和开口空隙,在饱水冻融循环作用下,开口空隙充满自由水分,水结冰后体积增大,产生膨胀力^{[4,5,15,16,17]} ...

... 在反复冻融循环作用下,孔隙壁承受冻胀压力和渗透压力,使沥青与集料的粘结力持续衰减,结构将变得松散,导致孔隙壁受损开裂^{[4,5,15,16,17]} ...

2012

0.0

... 成型的沥青混合料内部存在一定的闭口空隙和开口空隙,在饱水冻融循环作用下,开口空隙充满自由水分,水结冰后体积增大,产生膨胀力^{[4,5,15,16,17]} ...

... 在反复冻融循环作用下,孔隙壁承受冻胀压力和渗透压力,使沥青与集料的粘结力持续衰减,结构将变得松散,导致孔隙壁受损开裂^{[4,5,15,16,17]} ...

0.0

... 成型的沥青混合料内部存在一定的闭口空隙和开口空隙,在饱水冻融循环作用下,开口空隙充满自由水分,水结冰后体积增大,产生膨胀力^{[4,5,15,16,17]} ...

... 在反复冻融循环作用下,孔隙壁承受冻胀压力和渗透压力,使沥青与集料的粘结力持续衰减,结构将变得松散,导致孔隙壁受损开裂^{[4,5,15,16,17]} ...

... 反复冻融循环作用后,混合料空隙被撑大,影响粗集料的相互嵌挤,混合料在压缩破坏时骨架变形增大^[4,7,17] ...

2011

0.0

... 为此,本文利用非线性指数模型对抗压回弹模量进行分析,指数模型如下所示^[18,19]: ...

... ²值评价拟合参数的有效性^[18,19] ...

2002

0.0

... 为此,本文利用非线性指数模型对抗压回弹模量进行分析,指数模型如下所示^[18,19]: ...

... ²值评价拟合参数的有效性^[18,19] ...

2000

0.0

... 已有研究表明^[3,20],结构层系数SN可以很好地反映路面结构的承载能力 ...

... 普遍应用的沥青面层系数计算经验方程如下^[20]: ...

2009

0.0

... 而强度分析主要处理关于路面结构强度的材料性能与结构设计^[21] ...