弹性模量是材料测试中最基本的力学参数之一, 主要表征材料的刚度, 体现材料抵抗弹性变形的能力^{[1, 2]}。除此之外, 在表征材料硬度、耐磨性、残余应力、热应力等参数时, 弹性模量也是不可或缺的物理参数^{[3, 4]}。目前弹性模量的测量方法主要有静态法、动态法以及近年兴起的压入法三大类^{[3, 4, 5]}。静态法是指利用胡克定律确定弹性模量, 最常见的是静态拉伸法, 用应力-应变起始阶段的正切来估算弹性模量值, 方法简单。但是此方法对于脆性材料应用较少, 因为脆性材料弹性模量很高, 在受力过程中, 缺乏自身形变机制, 对轴向的偏心载荷无法通过自身的塑性变形来调节, 附加弯曲应力很大, 可能造成较大的测量误差^[6]。动态法是利用材料的共振频率来确定弹性模量, 如超声波速法和簧片振动法^[7]。动态法为无损测试, 但是精度较差, 成本较高, 且超声波速法反映的是样品上测试点附近区域的弹性性能, 存在一定局限性^{[8, 9]}。压入法是以一金刚石压头压入材料中, 通过载荷-压入位移曲线来求得弹性模量, 最典型的是纳米压入法, 但是该方法存在明显的基体效应、压痕尺寸效应等问题, 对测量结果也存在较大的影响^{[10, 11]}。

四点弯曲测试法是一种常见的力学测试方法, 指将试样放在有一定距离的两个支撑点上, 在离两个支撑点的中点相同距离上对试样施加载荷, 试样在四个接触点的作用下发生四点弯曲变形^[12]。四点弯曲测试法的试样为立方体结构(也可测试薄膜), 试样制备过程简单, 装夹方便, 且不局限于塑性材料, 针对脆性材料我国也有相应的试验规范。四点弯曲测试法得到的是整块材料的弹性模量, 这点是与超声波速法、纳米压入法等测试方法的显著区别之处。目前常见的有挠度计法、应变片法等, 但是都不利于仪器的自动化测量。针对以上情况, 采用四点弯曲法准确测试材料的弹性模量是有意义的, 也是有必要的。本文利用自主研制的小型四点弯曲测试装置分析和建立了一种块体材料的四点弯曲自动测量法, 并通过多种材料的试验和对比分析验证了此方法的可行性。

四点弯曲法的受力方式如图1所示, 最大弯矩分布在试样上一个较大的范围内, 两个内支撑点之间无剪应力的影响, 处于纯弯曲状态^[6], 而三点弯曲加载方式使被测试样很小的部分承受最大载荷, 某些部位的缺陷不易显示出来^[13]。Brancheriau等^[14]采用三点弯曲法测试木质样品的弹性模量时, 发现剪切作用的影响并非是可以忽略的因素, 三点弯曲法相比四点弯曲法会低估最后的测量值。Mujika^[15]的研究也发现对于越厚的试件, 三点弯曲法和四点弯曲法取得材料的弹性模量值相差越大, 并推测这个差异可能源自于三点弯曲中剪切作用的影响。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 四点弯曲试样受力情况及剪力图和弯矩图Fig.1 Shear diagram and moment diagram of four-point bending test

自动测试法是指利用位移测量装置在加载过程中自动同步记录材料弹性阶段的加载支点处的位移。通过弯曲的挠曲线连续性条件, 可以得到弹性阶段此位移与载荷的关系:

f=Fl23ls-4l)12EI5

式中:f为内支点处试样的变形量。由上式可以推出自动测试法弹性模量的计算公式。

2.1 四点弯曲测试装置

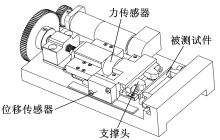
本文采用自主研制的小型四点弯曲装置进行测试, 图2为测试装置示意图。仪器采用的力传感器量程500 N, 非线性误差在0.1%以下, 在测试前经过M1级精度等级的标准砝码校准。测试载荷和标准砝码的对比情况如下:砝码分别为1、2、5、10、20 kg时, 对应载荷分别为9.72、19.68、49.22、97.88、196.43 N, 表明力传感器的精度较好。仪器采用非接触式位移传感器(即磁栅尺)测试压头处的位移。位移传感器分辨率为1 μ m, 测试前经过Keyence公司生产的LK-G10型激光位移传感器(分辨率可达10 nm)校准。校准时任取0.3 mm的行程范围进行测试, 同时记录位移传感器和激光传感器的读数。图3显示了位移传感器示数与激光传感器示数之间的误差值, 最大位移误差小于6 μ m, 误差率小于2%, 能够满足仪器的使用要求。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 采用的小型四点弯曲测试设备简图Fig.2 Engaged small size four-point bending test equipment

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 位移传感器的标定误差Fig.3 Calibrated error of displacement sensor

2.2 应变片法测定机架柔度

测试仪器的支撑头采用T10工具钢材料制成, 其硬度、强度均优于一般被测材料, 所以在测试试样弹性模量时支撑头材料不会发生屈服, 保证测试的一致性和准确性。但需要注意的是, 因为此种方法的位移量采用的是内支撑头处位移传感器的测量值, 支撑头及机座的变形也不可忽略, 如图4所示。为得到精确的弹性模量值, 首先必须消除测试过程中总体机架的变形, 试样真实变形与机架柔度的关系为:

f=S-C1F-C2F6C=C1+C27

式中:S为位移传感器测量的位移; C₁为内支撑头柔度; C₂为外支撑头及机座柔度; C为机架总柔度。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 机架变形示意图Fig.4 Schematic diagram of frame deformation

为得到准确的机架柔度参数, 采用在被测试样上贴应变片的方法。结合式(3)(4)(5)(7), 可得试样应变与机架柔度的关系:

ε=3h(f-CF)3ls-4l)l8

采用微晶玻璃陶瓷材料进行初步四点弯曲试验, 微晶玻璃陶瓷的尺寸为32.5 mm´ 6.4 mm´ 1.2 mm, 四点弯曲装置的内外跨距分别设定为10 mm和25 mm。选用长度为1 mm的电阻应变片, 贴在被测试样的中心。应变测试仪选用扬州晶明科技有限公司生产的JM3815型静态应变测试系统。

开始四点弯曲测试, 选取加载速率为0.06 mm/min。在记录载荷和位移信息的同时, 也实时读取相应的应变信号, 应变与时间的关系曲线如图5所示。根据式(8)求得机架柔度C=2.8246× 10^-4mm/N。最后求得所测微晶玻璃陶瓷的弹性模量为49.6 GPa。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 应变与时间的关系曲线Fig.5 Strain-time curve

图6为机架柔度标定前后的载荷-位移曲线对比, 通过线性回归分析, 标定后的直线斜率有不小的增加。根据式(6)(7)可以推出当弯曲载荷为20 N时, 标定后的位移为0.130 mm, 而位移传感器测得的位移值为0.136 mm, 二者比值为0.956, 误差范围在5%以内, 符合测试仪器的行业使用标准, 说明自主研制的四点弯曲测试装置的刚性较好^[16]。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 标定前后的载荷-位移曲线对比Fig.6 Load-displacement curve before calibration versus after calibration

为验证所采用四点弯曲自动测试法的准确性以及适用材料的多样性, 本文分别采用已知标准弹性模量值的微晶玻璃陶瓷、6061铝合金、c11000紫铜、K9光学玻璃四种材料进行了四点弯曲测试, 所选材料兼顾了塑性和脆性材料。因为同一牌号不同厂家材料的化学成分、热处理方法等因素都会对材料的弹性模量造成影响, 所以所采用四种材料试样的标准弹性模量值都分别来自于相同材料的测试结果, 以保证测试参考值的准确性。其中6061铝合金、c11000紫铜材料的标准弹性模量分别是通过制作标准试样在国家钢铁材料测试中心的标准拉伸测试仪上取得的, K9光学玻璃材料的标准弹性模量值是在Agilent Technologies公司生产的Nano Indenter G200型纳米压痕仪上经压痕测试取得的, 而微晶玻璃陶瓷的标准弹性模量值如前所述, 是通过应变片法的四点弯曲测试取得的。

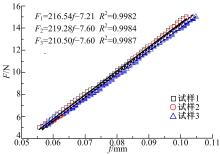
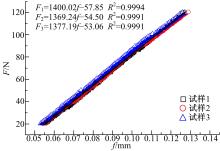
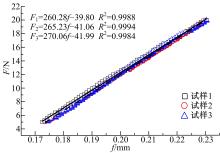
为了提高测试结果的精确性, 每种材料试验3次。其中6061铝合金和c11000紫铜采用线切割加工而成, 微晶玻璃陶瓷和K9光学玻璃为厂家提供。测试前每个试样的尺寸均采用游标卡尺进行测量。四点弯曲装置的内外跨距设置如下:内外跨距分别为10 mm和25 mm。4种材料弹性阶段的载荷-位移曲线如图7~图10所示, 所选取载荷-位移曲线的线性回归系数均接近1。每种材料三次试验的曲线斜率相近, 也间接证明了仪器的测试重复性较好。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 微晶玻璃陶瓷标定后的载荷-位移曲线Fig.7 Load-displacement curves of machinable glass ceramic after calibration

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 6061铝合金标定后的载荷-位移曲线Fig.8 Load-displacement curves of 6061 Al alloy after calibration

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 c11000紫铜标定后的载荷-位移曲线Fig.9 Load-displacement curves of c11000 Cu alloy after calibration

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 K9光学玻璃标定后的载荷-位移曲线Fig.10 Load-displacement curves of K9 optical glass after calibration

表1~表4为四种材料采用四点弯曲法得到的弹性模量测试结果, 其中标定前弹性模量一项是不考虑机架柔度时测得的弹性模量值。经过对比可以发现经过机架柔度标定后的测试结果十分接近材料的标准值, 其中相差最大的是c11000紫铜材料(111.9 GPa对123 GPa), 说明四点弯曲法的测试结果是可信的。另外, 试验也发现相较脆性材料(微晶玻璃陶瓷、K9光学玻璃)而言, 采用未经标定的四点弯曲自动测试法得到的塑性材料(6061铝合金、c11000紫铜)的结果误差较大, 会较大程度地低估材料的弹性模量值。这表明事先对测试仪器的机架柔度进行标定是很有必要的一项工作。

表1

Table 1

表1(Table 1)

表1 微晶玻璃陶瓷(32.5 mm× 6.4 mm× 1.2 mm)测试结果 Table 1 Test result of machinable glass ceramic (32.5 mm× 6.4 mm× 1.2 mm) 弹性模量 编号 1 2 3 标定前弹性模量/GPa 46.7 47.3 45.5 标定后弹性模量/GPa 49.6 50.2 48.2 标定后平均值/GPa 49.3 标准弹性模量/GPa 49.6

表1 微晶玻璃陶瓷(32.5 mm× 6.4 mm× 1.2 mm)测试结果 Table 1 Test result of machinable glass ceramic (32.5 mm× 6.4 mm× 1.2 mm)

表2

Table 2

表2(Table 2)

表2 6061铝合金(32 mm× 6 mm× 2 mm)测试结果 Table 2 Test result of 6061 Al alloy(32 mm× 6 mm× 2 mm) 弹性模量 编号 1 2 3 标定前弹性模量/GPa 52.9 52.1 52.3 标定后弹性模量/GPa 73.8 72.2 72.6 标定后平均值/GPa 72.8 标准弹性模量/GPa 72.6

表2 6061铝合金(32 mm× 6 mm× 2 mm)测试结果 Table 2 Test result of 6061 Al alloy(32 mm× 6 mm× 2 mm)

表3

Table 3

表3(Table 3)

表3 c11000紫铜(32 mm× 6 mm× 1 mm)测试结果 Table 3 Test result of c11000 Cu alloy (32 mm× 6 mm× 1 mm) 弹性模量 编号 1 2 3 标定前弹性模量/GPa 102.3 104.1 105.9 标定后弹性模量/GPa 109.8 111.9 114.0 标定后平均值/GPa 111.9 标准弹性模量/GPa 123

表3 c11000紫铜(32 mm× 6 mm× 1 mm)测试结果 Table 3 Test result of c11000 Cu alloy (32 mm× 6 mm× 1 mm)

表4

Table 4

表4(Table 4)

表4 K9光学玻璃(28 mm× 6 mm× 1 mm)测试结果 Table 4 Test result of K9 optical glass (28 mm× 6 mm× 1 mm) 弹性模量 编号 1 2 3 标定前弹性模量/GPa 77.3 76.0 72.6 标定后弹性模量/GPa 81.5 80.1 76.3 标定后平均值/GPa 79.3 标准弹性模量/GPa 79

表4 K9光学玻璃(28 mm× 6 mm× 1 mm)测试结果 Table 4 Test result of K9 optical glass (28 mm× 6 mm× 1 mm)

本文在现有弹性模量测试方法的基础上, 建立了一种块体材料弹性模量的四点弯曲自动测试法, 可以在加载过程中利用位移传感器自动测量加载支点处的位移。并利用经过标定后的自主研制的四点弯曲测试装置测试了微晶玻璃陶瓷、6061铝合金、c11000紫铜、K9光学玻璃的弹性模量, 验证了测试方法的可行性。本文所采用的四点弯曲测试法简便易行, 测试结果稳定, 适合多种块体材料的力学性能表征需要。