装载机液压系统的传热仿真分析

引用本文

王剑鹏, 秦四成, 杨立光, 李武. 装载机液压系统的传热仿真分析. 吉林大学学报: 工学版, 2016, 46(1): 153-158
WANG Jian-peng, QIN Si-cheng, YANG Li-guang, LI Wu. Simulation analysis of heat transfer in the hydraulic system of loader. Journal of Jilin University Engineering and Technology Edition, 2016, 46(1): 153-158 复制到剪切板

Permissions

装载机液压系统的传热仿真分析

王剑鹏^1,², 秦四成¹, 杨立光³, 李武¹

1.吉林大学机械科学与工程学院,长春 130022

2.吉林市93057部队,吉林省吉林市 132102

3.水利部长春机械研究所,长春 130012

秦四成(1962-),男,教授,博士生导师.研究方向:工程车辆节能控制.E-mail:qsc925@hotmail.com

作者简介:王剑鹏(1977-),男,工程师,博士研究生.研究方向:工程车辆节能技术.E-mail:jpwang07@mails.jlu.edu.cn

基金:国家科技支撑计划项目(2013BAF07B04)

摘要

为解决装载机夏天工作中液压系统过热问题,提出了将集总参数法用于液压系统解决传热问题的方法。采用集总参数法,建立液压系统传热问题的RC网络传热模型,编制计算程序。对某50型轮式装载机液压系统传热进行了仿真计算,并比较了仿真结果和试验数据。结果表明:采用集总参数法研究装载机液压系统的传热问题,其仿真结果的精度能够满足工程要求,模型的准确度满足工程设计需要,对液压系统的设计和改进具有指导作用。

关键词: 仪器仪表技术; 液压系统; 集总参数法; 传热; 装载机

中图分类号:TH243 文献标志码:A 文章编号:1671-5497(2016)01-0153-06

Simulation analysis of heat transfer in the hydraulic system of loader

WANG Jian-peng^1,², QIN Si-cheng¹, YANG Li-guang³, LI Wu¹

1.College of Mechanical Science and Engineering, Jilin University, Changchun 130022, China

2.Jilin 93057 Unit,Jinlin 132102,China

3.Changchun Machinery Research Institute of Ministry of Water Resources, Changchun 130012,China

Abstract

In order to solve the overheating problem in the hydraulic system of loader working in summer, the lumped parameter method is introduced to study the heat transfer in the hydraulic system. A RC network of heat transfer model is established using the lumped parameter method, and the computational program is developed. The heat transfer in the hydraulic system of a 50 type wheel loader is simulated, and the simulating results are compared with test data. Results show that the simulation precision can satisfy engineering demand and the accuracy of the model can meet the needs of engineering design. This study provides valuable reference to the design and improvement of the hydraulic system of loader.

Keyword: technology of instrument and meter; hydraulic system; lumped parameter method; heat transfer; loader

Show Figures

装载机液压系统工作时, 由于存在泄漏、摩擦、溢流等功率损失, 会产生大量热量, 使油温升高。对于较大功率的装载机, 由于系统的功率损失较大, 在铲装循环作业时液压系统效率仅为35.8%^[1]。同时受结构、重量等条件的限制, 液压油箱的体积不能过大, 单靠自然冷却无法满足系统的散热要求, 所以在液压系统中设置液压油散热器来进行强制散热, 但装载机的液压系统还是容易出现过热问题。特别是在夏季环境温度较高的情况下, 液压系统的油温过高会导致工作效率下降, 使液压元件的使用寿命降低^{[2, 3]}。

目前, 国内针对装载机液压系统热平衡的研究工作相对较少, 且研究方法主要以试验为主, 但装载机热平衡试验重复操作性较差。由于装载机液压系统的复杂性, 要对其传热进行研究, 采用一般的三维传热数值计算难以完成^{[4, 5]}。本文以装载机液压系统为研究对象, 应用集总参数法, 建立RC网络传热模型^[6], 并编制了计算程序; 采用本文模型对某50型轮式装载机进行了计算机仿真, 并将仿真结果与试验值进行了对比。

1 装载机液压系统传热理论分析

1.1 传热理论

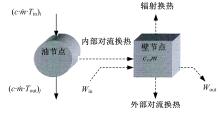
当固体内部的导热热阻远小于其表面的对流换热热阻时, 固体内部的温度趋于一致, 以至可以认为整个固体在同一瞬间均处于同一温度下, 这种忽略物体内部导热热阻的简化分析方法称为集总参数法。

集总参数法中的无量纲参数称为毕渥数:

$\begin{matrix} Bi = \frac{h (V / A)}{k} (1) \end{matrix}$

式中:V是固体体积; A是固体表面积; h是对流换热系数; k是导热系数。

Bi也可看作是内部导热热阻(V/A)/k与外部对流热阻(1/h)的比值。一般认为当Bi< 0.1时, 可以应用集总参数法解决工程传热问题, 计算精度可以满足工程计算要求^[7]。

1.2 液压元件传热原理

基于集总参数模型, 液压元件可以看作含有一定容积的液压容腔, 将液压容腔内的油液作为油节点, 外壁作为质量节点。油节点中一定质量、温度的液压油流进和流出液压容腔, 反映液压油的热运动; 质量节点描述传导、对流和辐射三种传热方式的热运动^[7]。

图1描述了一般液压元件的传热原理, $\begin{matrix} \overset{\cdot}{m} \end{matrix}$ 代表流进、流出油节点的液压油质量流量; W_in代表由于液压油的流动压力损失等产生的损失功; W_out代表对外界做功。

	Figure Option View Download New Window
	图1 液压元件传热原理Fig.1 Heat transfer principle of hydraulic components

2 装载机液压系统传热计算

2.1 液压元件和管路传热计算

装载机液压系统传热部件主要包括:液压泵、液压阀、液压油缸、液压管路、液压油箱和液压油散热器。

由于液压系统中液压油采用强制循环方式, 所以液压油与管路的换热主要是强制对流换热。

管槽内层流强制对流传热采用Sieder-Tate关联式^[8]:

$\begin{matrix} N u_{f} = 1.86 {(\frac{R e_{f} P r_{f}}{l / d})}^{\frac{1}{3}} {(\frac{η_{f}}{η_{w}})}^{0.14} (2) \end{matrix}$

管槽内湍流强制对流传热应用Dittus-Boelter关联式:

$\begin{matrix} N u_{f} = 0.023 R {e_{f}}^{0.8} P {r_{f}}^{0.4} {(\frac{η_{f}}{η_{w}})}^{n} (3) \end{matrix}$

式中:Re为雷诺数; Pr为动量扩散能力与热量扩散能力的一种量度; l为管路长度; d为管路直径; η 为动力黏度; f、w下标分别表示流体平均温度和壁面温度。

液压元件和管路外侧强制对流关联式为:

$\begin{matrix} Nu = CR e^{n} P {r_{f}}^{\frac{1}{3}} (4) \end{matrix}$

式中:C和n为常数, 由实验数据确定; 定性温度为(t_w+ $\begin{matrix} t_{\infty} \end{matrix}$ )/2。

液压元件和管路导热计算式为:

$\begin{matrix} Φ = \frac{2 πλl (t_{1} - t_{2})}{\ln (r_{2} / r_{1})} (5) \end{matrix}$

式中:t₁、t₂为液压管路内、外壁面温度; r₁、r₂为液压管路内、外壁直径; λ 为液压管路导热系数。

2.2 液压油散热器传热计算

液压油散热器的传热采用ε -NTU法^[7], 其传热量及传热单元数分别为:

$\begin{matrix} \begin{matrix} Φ = ε {(c q_{m})}_{\min} (t_{3} - t_{4}) (6) \\ NTU = \frac{kA}{{(c q_{m})}_{\min}} (7) \end{matrix} \end{matrix}$

式中:ε 是散热器的效能; $\begin{matrix} {(c q_{m})}_{\min} \end{matrix}$ 是散热器两侧冷、热流体中热容小的流体热容; t₃、t₄分别代表热、冷流体的入口温度; k是散热器传热系数; A是散热器换热面积。

2.3 液压油物理属性计算

在液压系统RC网络传热模型计算过程中, 经常调用油液属性计算函数。装载机使用的液压油为HM46抗磨液压油, 该种液压油试验数据拟合公式如下:

密度(kg/m³):

$\begin{matrix} ρ = 870 - 0.7 t \end{matrix}$

运动黏度(m²/s):

$\begin{matrix} \begin{matrix} lnv = - 9.3447 + 2.9006 lnt - 0.9397 {(lnt)}^{2} + \\ 0.04844 {(lnt)}^{3} \end{matrix} \end{matrix}$

定压比热容[J/(kg· K)]:

$\begin{matrix} c_{p} = 1940 + 3.4 t \end{matrix}$

热导[W/(m²· K)]:

$\begin{matrix} λ = 0.1755 - 0.000335 t 。 \end{matrix}$

3 装载机液压系统传热模型

液压系统元件定义为有限个节点, 每个节点内温度被假设为一致的。对于每个节点, 根据能量守恒定律可以得到下面公式:

$\begin{matrix} \begin{matrix} c_{v, i} m_{i} \frac{T_{j}^{t + 1} - T_{i}^{t}}{Δt} = \overset{h eattransfer}{\sum_{i}} \frac{T_{i}^{t + 1} - T_{\infty}^{t + 1}}{R_{i}^{t}} + \sum_{j} \frac{T_{j}^{t + 1}}{R_{i, j}^{t}} - \\ \sum_{j} \frac{T_{i}^{t + 1}}{R_{i, j}^{t}} + \sum_{i} W^{t} (8) \end{matrix} \end{matrix}$

式中:T为节点温度; $\begin{matrix} T_{\infty} \end{matrix}$ 为环境温度; R为热阻; W为节点对外界做功量; m为质量; c_v为定容比热; 下标i、j代表节点; 下标t+1和t为当前和先前的时间步长; Δ t为时间步长大小。

传热模型中的热容、热阻表达式如下:

热容:

$\begin{matrix} C = c \cdot m \end{matrix}$

平壁传导热阻:

$\begin{matrix} R = δ / (λA) \end{matrix}$

圆筒壁传导热阻:

$\begin{matrix} R = \frac{\ln (d_{2} / d_{1})}{2 πλL} \end{matrix}$

对流热阻:

$\begin{matrix} R = 1 / (h A) \end{matrix}$

辐射热阻:

$\begin{matrix} R = \frac{(T_{2} - T_{1})}{εσ F_{21} A_{s} (T_{2}^{4} - T_{1}^{4})} \end{matrix}$

流入(流出)节点热阻:

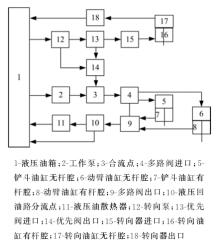
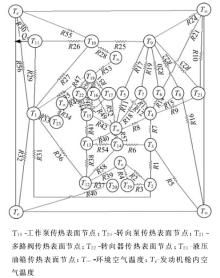
$\begin{matrix} R = 1 / (c \overset{\cdot}{m}) \end{matrix}$

应用集总参数模型建立50型装载机液压系统热平衡仿真模型, 装载机为双泵合流转向优先型液压系统。将液压系统分为18个流动节点和5个传热表面节点。为计算方便, 将装载机的液压油缸简化为一个无杆腔节点和一个有杆腔节点。多路阀分为多路阀进口节点和多路阀出口节点; 转向器分为转向器P口节点和转向器T口节点; 优先阀分为优先阀CF节点和优先阀EF节点, 如图2所示。

	Figure Option View Download New Window
	图2 装载机液压系统流动节点模型Fig.2 Node model of loader hydraulic system

多路阀和转向器到散热器之间液压管路主要用来与发动机舱内空气换热, 其他部分与环境空气换热, 见图3。

	Figure Option View Download New Window
	图3 装载机液压系统RC网络传热模型Fig.3 RC network of heat transfer model of loader hydraulic system

依据式(7)建立多路阀进、出口和液压油散热器传热模型, 其余节点建模方法同上。

多路阀进口节点:

$\begin{matrix} \begin{matrix} C_{dp} \frac{d T_{dp}}{dt} = \frac{1}{R_{7}} (T_{c} - T_{dp}) - \frac{1}{R_{12}} (T_{dp} - T_{h 1}) - \\ \frac{1}{R_{13}} (T_{dp} - T_{r 1}) - \frac{1}{R_{14}} (T_{dp} - T_{h 2}) - \\ \frac{1}{R_{15}} (T_{dp} - T_{r 2}) - \frac{1}{R_{8}} (T_{dp} - T_{\infty}) - \\ \frac{1}{R_{9}} (T_{dp} - T_{ds}) + N_{dp} (9) \end{matrix} \end{matrix}$

R₇= $\begin{matrix} \frac{1}{c_{oil} {\overset{\cdot}{m}}_{c - dp}} \end{matrix}$ ; R₁₂= $\begin{matrix} \frac{1}{c_{oil} {\overset{\cdot}{m}}_{dp - h 1}} \end{matrix}$ ; R₁₃= $\begin{matrix} \frac{1}{c_{oil} {\overset{\cdot}{m}}_{dp - r 1}} \end{matrix}$ ;

R₁₄= $\begin{matrix} \frac{1}{c_{oil} {\overset{\cdot}{m}}_{dp - h 2}} \end{matrix}$ ; R₁₅= $\begin{matrix} \frac{1}{c_{oil} {\overset{\cdot}{m}}_{dp - r 2}} \end{matrix}$ ; R₉= $\begin{matrix} \frac{1}{h_{1} \cdot A_{1}} \end{matrix}$ ;

R₈= $\begin{matrix} {(\frac{1}{h_{1} \cdot A_{1}} + \frac{\ln (d_{2} / d_{1})}{2 πλL} + \frac{1}{h_{2} \cdot A_{2}})}_{pipe}^{- 1} \end{matrix}$

式中:N_dp是多路阀入口损失功率; R₁₂、R₁₃、R₁₄、R₁₅是节点间流动热阻; R₈是合流节点到多路阀之间管路传热热阻; R₉是多路阀进口节点内液压油与外表面对流换热热阻。

多路阀出口节点:

铲斗无杆腔进油:

$\begin{matrix} \begin{matrix} C_{dt} \frac{d T_{dt}}{dt} = \frac{1}{R_{19}} (T_{dr 1} - T_{t}) - \frac{1}{R_{23}} (T_{dt} - T_{ds}) - \\ \frac{1}{R_{24}} (T_{dt} - T_{\infty}) + N_{dt} (10) \\ R_{24} = {(\frac{1}{h_{1} \cdot A_{1}} + \frac{\ln (d_{2} / d_{1})}{2 πλL} + \frac{1}{h_{2} \cdot A_{2}})}_{pipe}^{- 1} \end{matrix} \end{matrix}$

铲斗无杆腔回油:

C_dt $\begin{matrix} \frac{d T_{dt}}{dt} \end{matrix}$ = $\begin{matrix} \frac{1}{R_{17}} \end{matrix}$ (T_dr₁-T_t)- $\begin{matrix} \frac{1}{R_{23}} \end{matrix}$ (T_dt-T_ds)-

$\begin{matrix} \frac{1}{R_{24}} \end{matrix}$ (T_dt- $\begin{matrix} T_{\infty} \end{matrix}$ )+N_dt

动臂无杆腔进油:

C_dt $\begin{matrix} \frac{d T_{dt}}{dt} \end{matrix}$ = $\begin{matrix} \frac{1}{R_{22}} \end{matrix}$ (T_dr₂-T_t)- $\begin{matrix} \frac{1}{R_{23}} \end{matrix}$ (T_dt-T_ds)-

$\begin{matrix} \frac{1}{R_{24}} \end{matrix}$ (T_dt- $\begin{matrix} T_{\infty} \end{matrix}$ )+N_dt

动臂无杆腔回油:

C_dt $\begin{matrix} \frac{d T_{dt}}{dt} \end{matrix}$ = $\begin{matrix} \frac{1}{R_{20}} \end{matrix}$ (T_dh₂-T_t)- $\begin{matrix} \frac{1}{R_{23}} \end{matrix}$ (T_dt-T_ds)-

$\begin{matrix} \frac{1}{R_{24}} \end{matrix}$ (T_dt- $\begin{matrix} T_{\infty} \end{matrix}$ )+N_dt

式中:N_dt是多路阀出口损失功率; R₂₃是多路阀内油液与外壁对流换热热阻; R₂₄是油缸到多路阀T口节点之间管路传热热阻。

液压油散热器节点:

$\begin{matrix} \begin{matrix} C_{r} \frac{d T_{r}}{dt} = \frac{1}{R_{26}} (T_{d} - T_{r}) - \frac{1}{R_{29}} (T_{r} - T_{t}) - \\ \frac{1}{R_{30}} (T_{r} - T_{e}) - Q_{rout} + N_{r} (11) \\ R_{29} = \frac{1}{c_{oil} {\overset{\cdot}{m}}_{r - t}}; R_{26} = \frac{1}{c_{oil} {\overset{\cdot}{m}}_{r - t}}; \\ R_{30} = {(\frac{1}{h_{1} \cdot A_{1}} + \frac{\ln (d_{2} / d_{1})}{2 πλL} + \frac{1}{h_{2} \cdot A_{2}})}_{pipe}^{- 1} \end{matrix} \end{matrix}$

式中:N_r是液压回油管路分流块节点到液压油散热器节点之间管路损失功率; R₃₀为液压回油管路分流块节点到液压油散热器节点之间管路传热热阻。

$\begin{matrix} Q_{rout} = φ (12) \end{matrix}$

利用散热器厂家风洞试验得到的散热器传热系数k, 由式(7)计算得到NTU值, 根据文献[9], 查表得到ε , 根据式(6)计算散热器换热量。

4 实验验证

根据建立的装载机液压系统RC网络传热模型, 按照装载机I形铲装循环试验工况的要求, 对装载机液压系统油温进行仿真, 通过与试验数据的对比验证模型精度。

4.1 计算程序设计

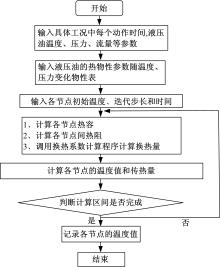
应用集总参数模型建立的装载机液压系统RC网络传热模型由23个常微分方程组成, 本文基于Matlab软件, 编写求解程序, 借助该软件中ode45函数, 采用Runge-kutta方法求解方程。程序首先输入环境空气温度, 液压油初始温度以及I形铲装循环试验工况压力、流量等参数; 然后输入液压油热物性参数随温度、压力变化的物性表; 最后设置迭代时间和步长。

4.2 边界条件

环境空气密度为1.093 kg/m³, 环境空气压力为0.102 MPa。HM46抗磨液压油20 ℃时密度为880 kg/m³, 比热为2093 J/(kg· K)。

装载机I形铲装循环试验工况:车速为11 km/h, 环境空气平均温度为34 ℃, 液压油初始温度为50.3 ℃, 发动机舱内温度为45 ℃, 液压油散热器前端空气温度为42 ℃, 风扇速度为9.28 m/s。

4.3 求解策略

传热模型计算过程如图4所示。

	Figure Option View Download New Window
	图4 传热模型计算过程Fig.4 Calculation process of heat transfer model

4.4 试验方案

(1)试验内容

制定装载机I形铲装循环作业试验工况的热平衡试验方案。实时同步测量液压系统关键部位的压力、流量和温度以及液压油散热器液压油的流量、温度和冷却空气的风温、风速。

(2)试验设备

采用FLUKE2686网络数据采集器, 每秒可以采集150个数据点, 从而更全面、详细记录铲装循环工况中油液温度的变化。其他设备包括流量传感器、压力传感器、转速传感器、温度传感器、风速传感器、风速仪。

(3)试验工况

发动机额定转速下工作泵出口液压油流量为220 L/min, 转向泵出口液压油流量为150 L/min。为实现装载机液压系统最大热负荷, 约24~28 s内完成一个工作循环。发动机油门为最大, 变速箱为I-Ⅱ 挡, 铲装物料为沙石。环境温度为34 ℃, 大气相对湿度为74%, 大气压力为0.102 MPa。保证铲装时铲斗满斗率不低于95%。热平衡试验前要对装载机进行预热, 保证液压油温为(50± 5) ℃。

主机厂家进行装载机工业性试验时, 为提高作业频率, 一般采取如下动作顺序:①铲斗收斗动作; ②装载机直线后退; ③装载机直线前进, 同时动臂举升; ④铲斗卸载直到铲斗内物料卸载干净; ⑤装载机直线后退, 同时动臂下降。

4.5 计算结果

针对装载机I形铲装循环试验工况, 对液压系统进行温度仿真, 并将仿真结果与试验测量数据进行比较。

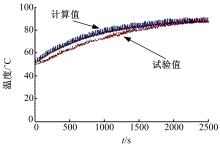
如图5所示, 装载机多路阀进口油温计算值与试验值比较一致。由于装载机在一个工作循环内液压系统损失功率不变, 液压系统散热功率随着油温升高而变大, 装载机在工作40多分钟后, 油温达到90 ℃, 此时生热功率等于散热功率, 系统趋于平衡。

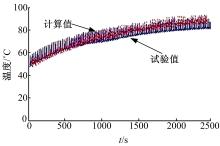
	Figure Option View Download New Window
	图5 多路阀进口油温Fig.5 Inlet oil temperature of direction control valve

如图6所示, 多路阀出口油温计算最大值为89.3 ℃, 试验最大值为92.06 ℃, 计算值和试验值都在9 ℃范围内波动上升。因为多路阀的节流功率损失比较大, 每个工作循环中液压系统都有高压溢流状态, 通过多路阀出口的液压油热容较小, 造成瞬间温升很高, 油温波动范围大。

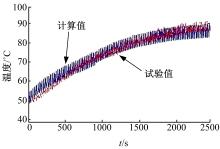
	Figure Option View Download New Window
	图6 多路阀出口油温Fig.6 Outlet oil temperature of direction control valve

如图7所示, I形铲装循环试验工况, 液压油初始油温为50.3 ℃, 液压油散热器进口油温计算值在工作40 min后趋于平衡, 最高温度为91.4 ℃, 进口油温试验最大值为92.06 ℃。

	Figure Option View Download New Window
	图7 散热器进口油温Fig.7 Inlet oil temperature of radiator

如图8, 液压油散热器出口油温初始值为47.2 ℃, 平衡后最大计算值为83 ℃, 最大试验值为84.2 ℃。

	Figure Option View Download New Window
	图8 散热器出口油温Fig.8 Outlet oil temperature of radiator

综上各图所示, 仿真结果与实验值符合较好, 仿真结果是可靠的, 能够满足实际工程要求。

5 结束语

采用集总参数法研究装载机液压系统的传热问题, 采用仿真模型计算的结果与试验数据比较一致, 说明模型的准确度满足工程设计需要, 对液压系统的设计和改进具有指导作用。但必须使每个控制容积的毕渥数满足关系式:Bi< 0.1, 才能保证计算精度。I形铲装循环试验工况中, 系统工作40 min后, 生热功率等于散热功率, 系统趋于平衡, 液压油温为90℃, 与环境温差为56℃。本文采用的建模方法还可以应用到发动机冷却系统、润滑系统热特性分析中。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	王剑鹏, 秦四成. 装载机液压系统性能与能耗分析[J]. 建筑机械, 2014(5): 114-118. Wang Jian-peng, Qin Si-cheng. Research on performance and power loss of hydraulic system for wheel loader[J]. Construction Machinery, 2014(5): 114-118. [本文引用:1]
[2]	秦四成. 国内装载机技术进步的思考[J]. 工程机械, 2010, 41(5): 48-50. Qin Si-cheng. Consideration on domestic loader technical progress[J]. Construction Machinery and Equipment, 2010, 41(5): 48-50. [本文引用:1]
[3]	王剑鹏, 秦四成, 赵克利. 50型轮式装载机液压系统的热平衡[J]. 吉林大学学报: 工学版, 2009, 39(3): 652-656. Wang Jian-peng, Qin Si-cheng, Zhao Ke-li. Study of characteristic of heat transfer for 50 wheel loader's hydraulic system[J]. Journal of Jilin University (Engineering and Technology Edition), 2009, 39(3): 652-656. [本文引用:1]
[4]	刘毅, 周大森, 张红光. 车用内燃机冷却系统动态传热模型[J]. 内燃机工程, 2007, 28(3): 49-51. Liu Yi, Zhou Da-sen, Zhang Hong-guang. A dynamic simulation model for cooling system of vehicle internal combustion engine[J]. Chinese Internal Combustion Engine Engineering, 2007, 28(3): 49-51. [本文引用:1]
[5]	Scott Timothy C, Phold Jason. Thermal modeling of power steering system performance[C]∥SAE Paper, 2008-01-1432. [本文引用:1]
[6]	Park Sungjin, Jung Dohoy. Numerical modeling and simulation of the vehicle cooling system for a heavy duty series hybrid electric vehicle[C]∥SAE Paper, 2008-01-2421. [本文引用:1]
[7]	Incropera Frank P. Fundamentals of Heat and Mass Transfer[M]. 葛新石, 叶宏译. 北京: 化学工业出版社, 2007. [本文引用:3]
[8]	Joerg Engelhardt. Thermal simulation of an aircrft fluid power system with hydraulic-electrical power conversion units[C]∥Proceedings of 1st FPIN-PhD Symp, Hamburg, Germany, 2000: 435-448. [本文引用:1]
[9]	杨世铭, 陶文铨. 传热学[M]. 4版. 北京: 高等教育出版社, 2006: 162-171, 371-376. [本文引用:1]

0.0

... 8%^[1] ...

2010

0.0

... 特别是在夏季环境温度较高的情况下,液压系统的油温过高会导致工作效率下降,使液压元件的使用寿命降低^[2,3] ...

2009

0.0

. 2009, 39(3):652-656

Study of characteristic of heat transfer for 50 wheel loader's hydraulic system

50型轮式装载机液压系统的热平衡

Wang Jian-peng , Qin Si-cheng , Zhao Ke-li.

王剑鹏, 秦四成, 赵克利

College of Mechanical Science and Engineering，Jilin University，Changchun 130022,China

Pressures and temperatures in the hydraulic system of the 50 type wheel loader were measured under different operating conditions to solve the overheating problem of the loader working in summer. Through the analysis of the experimental data it was found that the system overheating results from the wrong location of the hydraulic oil cooler, and the hydraulie oil flow rate through the cooler is insufficient to provide a dissipating power of the cooler required by the hydraulic system. Tests of the loader after the rearrangement of the oil cooler in the return circuit showed that the dissipating power of the relocated cooler conforms to the design target, and the total system operates normally.

解决某50型轮式装载机夏天工作中液压系统过热问题，测量了该装载机液压系统在各个工况下的压力和温度。通过分析测试数据，确定了系统过热的原因是系统中液压油散热器的布置不合理，通过散热器的液压油流量小，致使散热器散热功率无法达到设计要求。根据系统油温过高的原因，重新设计液压油散热器在回油路中的布置。经过试验证明，改进后的散热器散热功率符合设计指标，各系统工作正常。

... 特别是在夏季环境温度较高的情况下,液压系统的油温过高会导致工作效率下降,使液压元件的使用寿命降低^[2,3] ...

2007

0.0

... 由于装载机液压系统的复杂性,要对其传热进行研究,采用一般的三维传热数值计算难以完成^[4,5] ...

2008

0.0

... 由于装载机液压系统的复杂性,要对其传热进行研究,采用一般的三维传热数值计算难以完成^[4,5] ...

2008

0.0

... 本文以装载机液压系统为研究对象,应用集总参数法,建立RC网络传热模型^[6],并编制了计算程序 ...

2007

0.0

... 1时,可以应用集总参数法解决工程传热问题,计算精度可以满足工程计算要求^[7] ...

... 质量节点描述传导、对流和辐射三种传热方式的热运动^[7] ...

... -NTU法^[7],其传热量及传热单元数分别为: ...

2000

0.0

... 管槽内层流强制对流传热采用Sieder-Tate关联式^[8]: ...

0.0