作者简介:邱清盈(1970-),男,副教授,博士.研究方向:机械优化设计和创新设计方法,挖掘机优化设计、结构强度分析和测试.E-mail:medeslab@zju.edu.cn
针对挖掘机载荷谱难以实测获取,从而难以对其工作装置进行疲劳分析的问题,提出一种新的解决方法:首先通过对铲斗挖掘土壤过程进行仿真,获得挖掘阻力的完整变化过程,即挖掘阻力载荷谱;然后通过整机作业过程仿真,获得与上述挖掘阻力载荷谱相对应的工作装置各铰点载荷谱,并通过实测油缸压力进行对比验证;最后以经过验证的各铰点载荷谱实现工作装置的动臂和斗杆疲劳寿命分析。以某23 t液压反铲挖掘机为例,详述了采用上述方法对其工作装置进行疲劳分析的过程,计算出动臂和斗杆在典型作业循环工况下的最低疲劳寿命分别为105.978和106.47次,验证了所提方法的有效性。
It is hard to measure the load history of the working device of hydraulic excavator in fatigue analysis. To solve this problem a novel fatigue analysis method is proposed. First, the complete change process of digging resistance, named Digging Resistance Load Spectrum (DRLS), is obtained by simulating the digging process of soil with the bucket of hydraulic excavator. Second, according to the DRLS, the load history of each hinge of the working device is calculated by the operation simulation of a full typical working cycle of the excavator. The simulation results are then verified by comparing with the actual cylinder pressure measured from the experiment similar to the working condition in the simulation. Finally, the fatigue analysis of the boom and arm of the working device are accomplished with the verified load histories of the hinges. The effectiveness of the proposed method is demonstrated with the fatigue analysis process of the working device of a 23 t hydraulic backhoe excavator. The results come out that the minimum lives of the boom and arm are 105.978 and 106.47 cycles respectively.
当前以挖掘机为特定对象进行疲劳分析的研究非常少, 其主要难点在于很难通过实测获取载荷谱, 因此现有研究多采取简化或其他替代方式。例如:张卫国等[1]在对挖掘机进行疲劳分析时, 采用实测油缸压力反推挖掘阻力的最大值作为铲斗载荷驱动, 但将变化的油缸压力作用简化为单一的挖掘阻力作用导致求出的铰点载荷历程无法体现出油缸压力变化带来的影响, 而仅与挖掘位姿变化有关, 故而无法真实反应挖掘机所受载荷的变化过程; 周宏兵等[2]在通过动力学获取挖掘机铰点载荷历程时采用传统经验公式处理挖掘阻力, 虽然经验公式能大致反映铲斗挖掘阻力大小, 但无法真实反映出土壤与斗侧壁及斗底之间的摩擦阻力、土壤与土壤之间的剪切力等作用力的综合变化过程, 从而导致最终获取的载荷变化过程偏离实际; 朱连双、白瑞等[3, 4]则通过测试得到挖掘机工作装置几个危险点在典型工况下的应力时间历程, 然后经滤波和计数后参照光滑构件的S-N曲线推导疲劳寿命, 该方法由于工况数和测点数较少不能反应整机应力应变的变化过程。
针对现有研究的不足, 本文提出一种新的进行挖掘机工作装置疲劳分析的思路:通过铲斗挖掘土壤过程仿真和整机作业过程仿真, 获得工作装置各铰点的载荷时间历程, 经过验证后作为载荷谱实现工作装置的疲劳寿命计算。
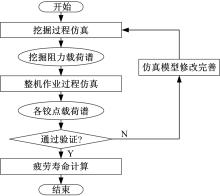
如上所述, 进行挖掘机工作装置疲劳分析的难点在于载荷谱的获取。为了解决这一问题, 提出了如图1所示的挖掘机工作装置疲劳分析流程, 其主要步骤为:
(1)挖掘过程仿真:建立挖掘机铲斗挖掘土壤过程的有限元仿真模型, 在显式动力学软件LS-DYNA中通过数值模拟计算, 求得整个挖掘过程中铲斗上所受挖掘阻力的完整变化过程, 即挖掘阻力载荷谱。
(2)整机作业过程仿真:建立挖掘机整机作业过程仿真模型, 以第一步中获得的挖掘阻力载荷谱作为载荷驱动, 在动力学仿真软件ADAMS中通过仿真获得典型作业循环工况下工作装置各铰点的载荷谱。
(3)载荷谱验证:由于挖掘过程的载荷变化会直接反映到工作装置三组油缸的压力波动, 即挖掘阻力变化与油缸压力变化之间存在对应关系, 因此虽然无法对上述仿真获得的挖掘阻力载荷谱和各铰点载荷谱进行直接验证, 但是可以通过对比实测油缸压力与仿真获得的油缸压力之间的误差来间接判断仿真获得的载荷谱是否准确可信。如果通过验证, 则可以用作后续的疲劳寿命计算, 否则需要返回第一步对挖掘过程仿真模型进行修正。
(4)工作装置疲劳寿命计算:以验证后的各铰点载荷谱, 在疲劳分析软件FE-SAFE中完成挖掘机工作装置的疲劳寿命计算。
土壤是挖掘机的工作对象, 土壤模型的优劣对于通过仿真获取挖掘阻力载荷谱的正确性有重要影响。目前公认具有较高精度和稳定性的土壤模型是显式动力学软件LS-DYNA中的* MAT_MOHR_COULOMB土壤本构模型[5], 该模型采用经典摩尔库伦屈服准则[6], 可适用于土壤、混凝土等类似特性材料的模拟。
由于目前在挖掘机挖掘土壤仿真方面的研究几乎没有, 因此在参考作用机理相似的刀具切削土壤研究的基础上[7, 8, 9], 为了兼顾计算效率和求解精度的要求, 在建立铲斗挖掘土壤模型时, 可采取如下处理策略:
(1)考虑铲斗挖掘土壤时的应力传播, 土壤模型应尽可能大, 但是在相同网格密度情况下, 过大的土壤模型将使有限元计算量大幅增加, 因此在实际建模时, 可根据铲斗尺寸, 将土壤模型设置为铲斗尺寸的4~5倍左右。
(2)由于铲斗尺寸远小于土壤模型, 因此可对其抽取中面, 以壳单元代替实体单元; 同时考虑到挖掘过程中铲斗变形很小, 可以将铲斗定义为刚性体, 这样可以显著提高求解效率。
(3)考虑到铲斗斗齿过尖, 当其作用于土壤时容易引起负体积等问题而造成求解错误甚至失败, 同时挖掘过程中主要是铲斗斗缘起到决定性作用, 因此在建模时可以将斗齿简化掉。
(4)网格划分时, 因为土壤及其流动域是主要关心对象, 所以它们的网格相较铲斗应该划分得更为细密。
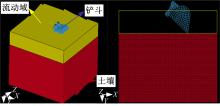
以江苏省常州市某挖掘机厂家的23 t挖掘机挖掘常州地区的粘土为例, 根据该型号挖掘机铲斗尺寸将土壤模型尺寸设置为5 m× 4 m× 2.5 m, 将用作土壤网格大变形流动的流动域设置为5 m× 4 m× 1 m, 最终形成的土壤挖掘初始模型如图2所示。
参照与江苏省常州市粘土特性基本相同的昆山地区土壤[10], 仿真中土壤材料属性取值如表1所示。铲斗材料为Q345, 其材料参数为:弹性模量为2.06× 105 MPa, 密度为7.85× 103 kg/m3, 泊松比为0.3, 屈服极限为600 MPa。
| 表1 粘土关键参数取值 Table 1 Key parameter values of clay |
由于在仿真过程中土壤网格会发生大变形, 是一个典型的几何非线性、材料非线性以及接触非线性的复杂分析问题, 因此应采用LS-DYNA中的任意拉格朗日-欧拉(ALE)算法, 以有效地解决网格大变形问题[11, 12]。
图3为挖掘机铲斗挖掘土壤的仿真过程:首先斗杆挖掘, 即铲斗在斗杆的带动下切入土壤, 与铲斗接触的土壤受到挤压, 然后斗杆-铲斗复合动作进行挖掘, 随着转动角度的增大, 铲斗开始推送土壤产生土壤积屑瘤; 最后铲斗挖掘, 将土壤积屑瘤慢慢装入斗中。
经过仿真得到全局坐标下挖掘阻力三向分力如图4所示, 因忽略偏载作用, 故Z向受力为0, 而X、Y向合力从0开始增大至92 kN后再减小, 变化趋势与实际挖掘规律相符。
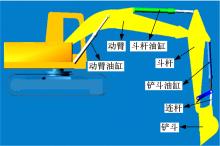
考虑到目前对工程机械作业过程仿真的研究已经很多且相对比较成熟[2, 13], 因此这里不再作赘述。挖掘机作业过程仿真的步骤主要包括:首先在Adams中建立如图5所示的挖掘机整机模型, 包括机构模型、液压系统模型和控制模型; 然后将图4挖掘阻力载荷曲线作用于铲斗尖, 并在三组油缸中设置压力传感器、在各铰点上设置力传感器以便获得仿真数据; 最后通过控制液压系统驱动三组油缸完成一个完整的作业过程仿真。
为了验证仿真获得的载荷谱的准确性, 对该厂家的某型23 t挖掘机挖掘常州地区的粘土进行了试验(见图6), 实测了作业循环过程中油缸的压力变化曲线。图7为实测与仿真获得的斗杆和铲斗油缸压力变化曲线的对比情况, 可以看到仿真与实测曲线基本一致, 只是在铲斗开始挖掘土壤阶段、挖掘满斗阶段以及卸载阶段实测值会有一定变化的冲击载荷, 其余阶段斗杆和铲斗油缸的压力平均误差分别小于7%和5%, 因此可以认为仿真获得的挖掘阻力载荷谱具有较好的准确性。这样, 可将作业过程仿真获得的各铰点载荷谱(见图8)用于后续疲劳分析。
挖掘机工作装置的损坏属于高周多轴疲劳, 目前关于高周多轴疲劳的损伤累积和寿命估算主要有三种方法:应力准则法、临界面准则法和能量准则法, 其中临界面准则法因建立在裂纹萌生和扩展机理之上而具有一定物理意义, 并被认为是一种较有效的高周多轴疲劳分析方法[14]。在疲劳分析软件FE-SAFE中集成了临界面准则法, 但FE-SAFE需要借助ANSYS等其他有限元软件完成前后处理工作。因此在对工作装置进行疲劳分析时, 首先在ANSYS中对工作装置进行单位铰点载荷下的静力分析, 然后将静力分析的应力结果和上文获得的铰点载荷谱导入FE-SAFE中完成工作装置的疲劳寿命计算, 最后在ANSYS中进行疲劳结果的后处理显示。
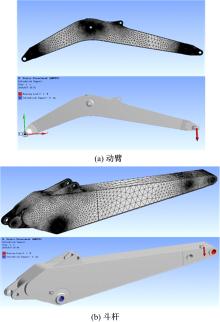
在ANSYS中分别建立液压挖掘机的动臂和斗杆有限元模型, 如图9所示, 材料均为Q345。依次在各铰点加载单位载荷分量并定义好约束后即可完成静力分析求解。
求解的结果文件包含了进行疲劳分析所需要的工装在各单位力作用下的应力张量等信息。
在FE-SAFE中将上述静力分析结果与相应的各铰点载荷时间历程关联, 依据软件提供的Seeger’ 材料数据估算方法, 用Q345材料的抗拉强度与弹性模量建立其S-N曲线, 采用BrownMiller临界面算法完成疲劳寿命计算, 将计算结果导入ANSYS中, 最终得到动臂和斗杆的疲劳寿命如图10所示。
由图10可以看出在典型作业循环工况下工作装置的损坏情况:对于动臂, 最早在动臂耳板处发生损坏, 最低寿命为105.978次, 经分析该部位是斗杆油缸作用力的直接承受者, 局部有应力集中且耳板厚度较薄, 故而最早损坏; 对于斗杆, 最早在其与动臂铰接的销轴四周及销轴内部发生损坏, 最低寿命为106.47次, 经分析该部位是斗杆箱体边缘与销轴的连接位置, 容易产生应力集中, 同时也是斗杆承受交变载荷的位置, 故而最早损坏。
该23 t挖掘机一次作业过程时间约为14 s, 假设挖掘机一天工作8 h, 一年工作365天, 则经过计算得出该挖掘机工作装置在连续工作462天后动臂首先发生损坏, 经过3.93年后斗杆发生损坏, 而其余位置基本可工作13.3年。这说明该挖掘机工作装置的局部结构设计还不够合理, 可以在疲劳分析的基础上作进一步的结构优化改进。
(1)通过挖掘过程仿真、整机作业过程仿真以及实测油缸压力进行验证等步骤, 有效地解决了挖掘机工作装置疲劳分析的载荷谱难以获取的问题。
(2)在此基础上, 提出了一种新的挖掘机工作装置疲劳分析流程, 以某23 t挖掘机为例, 说明了上述载荷谱获取方法和疲劳分析流程的有效性。
(3)建立的挖掘过程仿真模型, 既考虑了土壤性质、土壤与铲斗摩擦等关键因素, 又对土壤作用区域、铲斗模型等一些次要因素进行了必要的简化, 兼顾了求解精度和计算效率的要求, 为深入研究挖掘机与土壤之间的作用机理提供了一个较好的模型基础。
(4)提出的挖掘机工作装置的载荷谱获取方法和整个疲劳分析流程, 对其他工程机械或产品的疲劳分析也具有参考价值。
(5)由于挖掘机的动臂和斗杆尺寸较大、结构复杂, 直接或制作局部结构样件进行疲劳试验验证较为困难, 因此如何验证理论计算的疲劳寿命以及如何分析和修正流程中各环节的误差将是后续需要进一步深入研究的问题。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|