引用本文
田野, 邓宗全, 唐德威, 姜生元, 全齐全, 侯绪研. 月球次表层取心钻具功耗特性及地面模拟实验. 吉林大学学报: 工学版, 2016, 46(1): 166-171
TIAN Ye, DENG Zong-quan, TANG De-wei, JIANG Sheng-yuan, QUAN Qi-quan, HOU Xu-yan. Power consumption of lunar subsurface coring driller and earth environment stimulant experiments. Journal of Jilin University Engineering and Technology Edition, 2016, 46(1): 166-171  
Permissions
Copyright©2016, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
月球次表层取心钻具功耗特性及地面模拟实验
田野1,2, 邓宗全1, 唐德威1, 姜生元1, 全齐全1, 侯绪研1
1.哈尔滨工业大学 机器人技术与系统国家重点实验室,哈尔滨 150001
2.哈尔滨商业大学 轻工学院,哈尔滨 150028
唐德威(1966-),男,教授,博士生导师.研究方向:深空探测采样技术.E-mail:dwtang@hit.edu.cn

作者简介:田野(1981-),男,博士研究生.研究方向:深空探测采样技术.E-mail:tian8154@126.com

基金:国防领域科技重大专项项目(TY3Q20110005); 国家自然科学基金项目(51105092); 高等学校学科创新引智计划项目(B07018)
摘要

建立了月球次表层取心钻具功耗模型,制备了与真实月壤物理机械参数相近的模拟月壤作为被钻对象,通过钻进取心实验对理论模型进行验证,得到取心钻具的功耗特性曲线并确定低能耗钻进规程。实验结果表明,取心钻具钻进功耗理论模型能够正确反映实验曲线的变化趋势,可依据模型对钻具的钻进功耗进行预估。以保证高取心率为前提,在阻力矩允许范围内,适当降低钻具回转转速,可使取心钻具的钻进功耗降低。

关键词: 机械设计; 探月采样; 取心钻具; 功耗模型; 钻进规程
中图分类号:TH122,V44 文献标志码:A 文章编号:1671-5497(2016)01-0166-06
Power consumption of lunar subsurface coring driller and earth environment stimulant experiments
TIAN Ye1,2, DENG Zong-quan1, TANG De-wei1, JIANG Sheng-yuan1, QUAN Qi-quan1, HOU Xu-yan1
1.State Key Laboratory of Robotics and System,Harbin Institute of Technology,Harbin 150001,China
2.College of Light Industry,Harbin University of Commerce,Harbin 150028,China
Abstract

Soil sample with physical and mechanical properties similar to real lunar soil is prepared as the drilling object. The power consumption model of coring driller is proposed and verified by coring experiments. The lower power consumption drilling procedure is obtained by analyzing the power consumption curve. To ensure high cording rate, lower rotary speed can decrease the drilling power consumption in the allowable range of resistance moment of drilling. The data calculated from the proposed model is in good agreement with the drilling experiment results. Thus, the proposed model can be used to predict the drilling power consumption.

Keyword: mechanical design; lunar sampling; coring driller; power model; drilling regulation
0 引 言

我国的探月工程分为三个阶段, 到目前为止已经完成了“ 绕” 和“ 落” 两个阶段。第三阶段“ 回” 的任务之一是钻进到月球次表层以下指定深度并采集一定质量的月壤样品。月球环境的特殊性增加了钻取采样任务的难度, 为了保证任务顺利完成, 需要结合月球土壤的特性对采样钻具的钻进功耗进行研究, 并在地面环境下用模拟月球的土壤进行模拟实验。

目前, 美国和前苏联在大量的地面环境试验后, 使用取心钻具成功地完成了月球采样返回任务[1]。美国喷气推进实验室的Yoseph、Badescu等[2, 3]设计了一种超声波振动采样钻具, 该钻具能够以较小的功耗对岩石进行振动钻进采样, 但无法对松散的颗粒状月壤进行钻取采样。Marchesi等[4]研制的SD2采样钻具安装在Philae彗星探测器上, 通过回转和冲击能够对彗星表面进行破碎并采样, 由于结构限制采样质量较低。丁希仑等[5]设计了MRDD钻具, 采用多杆组接式结构可钻进到1.5 m深度, 但缺乏对MRDD钻具钻进功耗的实验研究。Glass等[6]研制的“ 破冰者” 钻具可钻入外星球表面以下1.8 m深度, 对冰层和岩土取样, 但取心率低, 且需要多次重复提钻动作。

本文基于以往的研究成果[7, 8, 9], 对月球取心钻具的功耗特性进行分析, 得到取心钻头和螺旋钻杆与月壤的相互作用的功耗模型, 通过对制备的模拟月壤进行钻进取心实验, 得到其功耗特性曲线以验证所建立的功耗模型的正确性, 并为我国探月工程中钻取采样任务所用的钻进策略制定提供参考。

1 次表层取心钻具工作原理

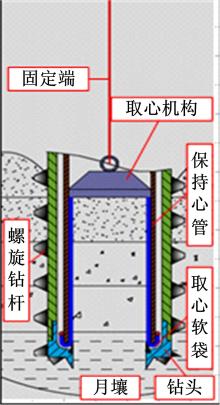
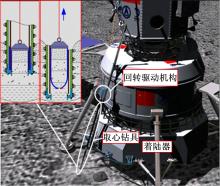
月球次表层取心钻具主要由取心钻头、螺旋钻杆和取心机构组成, 如图1所示。取心钻具安装在月球着陆器上, 如图2所示, 当着陆器降落到月面后, 取心钻具在回转驱动机构的驱动下钻入月球次表层。钻头的主要功能是破碎月壤和岩石, 在钻进过程中形成月壤样心; 螺旋钻杆的主要功能是输送被钻头破碎后的碎屑至钻孔外部, 为钻具的进尺运动提供空间; 取心机构的功能是将钻进过程中形成的月壤样心用取心软袋包裹住, 使其原有状态不受钻进运动扰动, 保持心管隔离软袋和钻具内壁, 以利于样心的提取。根据取心钻具的各部分功能, 将其钻进功耗分为取心钻头切削月壤和螺旋钻杆输土功耗两部分。

图1 取心钻具组成示意图Fig.1 Schematic diagram of coring drill tool

图2 取心钻具采样状态示意图Fig.2 Schematic diagram of coring drill tool working

2 模拟月壤参数确定及制备

月壤是覆盖在月球表面上的土壤, 是由月岩在经历长期的宇宙辐射、陨石撞击和高低温变化而形成的颗粒状碎屑[10]。由于月球没有大气层, 地层中没有液态水, 导致月壤在三相组成上与地球土壤差异较大, 即没有气相和液相, 但固相组成相同, 所以可采用土力学中对地球土壤的分析方法对月壤进行研究。而钻具钻进功耗特性仅涉及月壤的密度、孔隙率、内聚力和内摩擦角等物理力学参数。

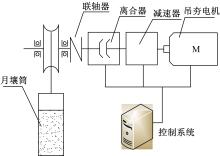
为了在地面环境下模拟钻取采样实验, 需要物理力学参数与真实月壤近似的模拟月壤。哈尔滨工业大学宇航空间机构及控制研究中心采用吊夯法制备模拟月壤[11], 制备装置由月壤筒、吊夯电机及释放装置、机架和控制系统组成, 如图3所示。

图3 月壤吊夯制备装置工作原理Fig.3 Lunar soil lifting compaction device

通过月壤制备装置的吊夯电机将装有模拟月壤的月壤筒吊起, 起吊高度为20 cm时离合器断电, 月壤筒做自由落体运动, 利用重力提高模拟月壤密度。冲击振动的次数为20次。此过程结束后, 再次对模拟月壤桶进行填充相同质量的模拟月壤, 并采用相同的制备工艺吊夯, 直至计算的密度达到真实月壤给定范围内结束。

通过计算和三轴剪切实验可以得到模拟月壤的主要物理力学参数, 如表1所示。由表1可知模拟月壤的相关参数在真实月壤[12, 13]参数范围内, 可以用于钻进取心实验。

表1 HITLS-1型月壤参数 Table 1 HITLS-1 simulation lunar soil parameters
3 次表层取心钻具钻进功耗模型
3.1 取心钻头切削功耗模型

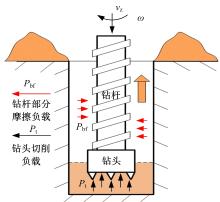
如图4所示, 当钻进月壤时, 钻头在钻进压力和回转转矩的作用下, 破坏月壤原有结构, 使月壤形成细小碎屑, 月壤碎屑在螺旋钻杆的回转作用下, 被输送至钻孔外部。根据美国和前苏联探月采样的成功经验, 取心钻具在钻进月壤过程中会使着陆器上的能量损失较大。在这一过程中切削的钻头阻力矩和钻杆的输土阻力矩是钻进能耗的主要组成部分。

图4 取心钻具钻进功耗组成示意图Fig.4 Schematic diagram of coring drill tool power consumpution

基于以往的研究[7, 8, 9], 取心钻头破碎月壤时的功耗模型主要是由切削具切削破碎月壤而产生的, 单一切削具所受到的阻力Ft是中心阻力Fc和侧向失效阻力Fl之和。

Ft=Fc+2Fl1Fc=(γd2+q)rtan(β+φ)+cd[tanβtan(β+φ)+cotβ]sin(αc+δ)+cos(αc+δ)tan(β+φ)+γdv2sinαc[sinβtan(β+φ)-cosβ]sin(αc+β)sin(αc+δ)+cos(αc+δ)tan(β+φ)·w　(2)Fl=16γdr2+12cdr[1+cotβcot(β+φ)]+12qr2cot(αc+δ)+cot(β+φ)·ρ'(3)

式中:d为每转切削量; q为均布载荷; γ 为月壤的容重; δ 为切削具与月壤的摩擦角; β 为月壤失效角; α c为切削具切削角; φ 为月壤内摩擦角; c为月壤内聚力; w为切削具宽度; ρ '为侧向失效区角度; r为中心失效区半径; v中心失效区月壤速度。

取心钻头的回转功耗为

Pt=ncFtRω4

式中:R为取心钻头的半径; ω 为取心钻具的回转角速度; nc为切削具个数。

3.2 螺旋钻杆输土功耗模型

钻杆输土的总功耗Mt由三部分组成:①月壤碎屑在螺旋面上运动而产生的摩擦阻力距M1; ②螺旋外端面转动时与孔壁产生的摩擦阻力距M2; ③螺旋槽内的碎屑运动时与螺旋槽底面的摩擦阻力距M3。则螺旋钻杆的总阻力矩为:

Mt=∑i=13nb·Mi5M1=πμp1h∫0z(D-h)Dcosαbγ2Sdz6M2=12S(D-2h)Dπp1ψμ∫0zgK0σv-hω12γD-h2)dz7M3=12SπK0(1-p1)μcosγs∫0zD2γdz8

钻杆总功耗为:

Pbf=Mtω9

式中:α b为钻杆螺旋升角; μ 为月壤与钻具的摩擦因数; p1为螺旋槽宽; h为螺旋径向高度; D为钻杆螺旋外径; S为钻杆螺旋导程; z为轴向钻进深度; ω 1为月壤在钻杆螺旋槽内的转速; K0为月壤侧压力系数; σ v为月壤自重应力; ψ 为月壤在螺旋槽内的充填率; γ s为螺旋微元合速度与水平方向夹角; nb为螺旋头数。

由于取心钻头和螺旋钻杆固连在一起, 两者产生的转矩是绕自身轴线的, 而两者转轴共线, 且都是阻碍取心钻具回转运动的主要原因。由式(4)和(9)可得到钻具钻进月壤时消耗的总功耗为:

P=Pt+Pbf10

4 取心钻具钻进功耗模拟实验
4.1 实验设备及方法

为了验证理论模型的正确性, 需要在实验室环境下进行模拟实验。实验采用哈尔滨工业大学宇航空间机构及控制研究中心研制的全参数月球深层钻取采样实验平台[14, 15], 如图5所示的实验平台由取心钻具、回转驱动装置、进尺驱动装置、机架和控制系统等组成。

图5 全参数月球深层钻取采样实验平台Fig.5 Lunar deep drilling test bed

待取心钻具钻进到1.7 m指定深度后停止钻进。提取所需数据并量取软袋内的月壤样心长度得到取心率, 如图6所示。

图6 内装有月壤样心的取心软袋实物图Fig.6 Soft bag with lunar soil

实验选用的HIT-2型取心钻头结构参数如下:切削具数量为4, 切削角为75° , 切削具刃宽为12 mm。钻杆结构参数如下:直径为0.032 m; 螺旋升角为14° ; 槽宽比为0.9。

4.2 实验结果及分析

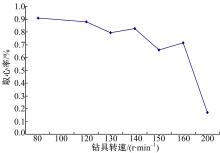
采用恒定的100 mm/min进尺速率, 并使转速在80~200 r/min范围内变化, 得到的取心率如图7所示, 从图7可知, 转速在80~120 r/min范围内取心率较高, 而我国探月采样返回任务应该以高取心率为主要目标, 这需要在保证较高取心率的前提下, 通过控制钻进规程使得钻进功耗最小。

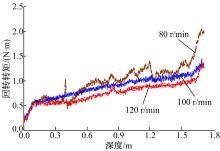
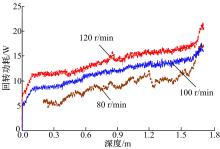
图7 取心率与转速曲线Fig.7 Coring rate and rotary curve

分别选取钻进规程参数为100 r/min-100 mm/min、80 r/min-100 mm/min、120 r/min-100 mm/min的3组实验数据进行分析, 提取回转转矩的数据如图8所示。在图8的数据基础上乘以对应的角速度, 得到如图9所示的功耗曲线。由转矩图8可知, 在进尺速度相同的条件下, 转速越慢转矩越大。原因是由于回转转速降低后, 使得钻头的切削具每转动一圈的切削量d增大, 导致切削功耗增大; 并且切削量增大了, 直接导致钻杆排土量增大, 使得螺旋槽内的充填率ψ 变大, 增大了螺旋槽内月壤与钻杆及孔壁的摩擦面积。由于转矩相差较小而转速相差较大, 当其转化成功耗曲线时, 钻进功耗随着转速的增加而增加。为了满足采样返回的任务目标, 可在保持高取心率的前提下, 适当降低转速, 以得到较小的钻进功耗。

图8 回转转矩曲线Fig.8 Rotary torque curve

图9 回转功耗曲线Fig.9 Rotary power consumpution curve

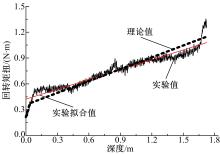
选择转矩最小的120 r/min曲线与理论值进行对比研究, 如图10所示。从图中可以看出转矩的理论值和实验值均随钻进的深度增加而增加。将实验曲线进行线性拟合, 得到如图10所示的直线, 拟合与实验值的拟合度平方为0.918, 说明拟合度较高。在不同深度上,

图10 理论值与实验值对比图Fig.10 Comparison of theoretical value and test value

对比转矩值的理论值与拟合值, 如表2所示, 通过计算两者的偏差可知, 两者偏差为-7.3%~7.9%, 偏差的平均值为0.09%, 偏差的标准差为6.028%, 其原因是由于模拟月壤在吊夯过程中密度不均匀, 导致实验值在初始阶段大于理论值, 而在末端低于理论值, 总体上围绕理论值上下波动。

表2 不同深度的理论值与实验值 Table 2 Theory and test on different depths
5 结 论

(1)以保证高取心率为目标的前提下, 在阻力转矩允许范围内, 适当降低钻具回转转速, 可使取心钻具的钻进功耗降低。

(2)在进给速度不变的条件下, 取心钻具的回转钻进功耗随速度的增加而增加, 而钻进阻力转矩随速度的减小而增大。

(3)建立的取心钻具回转功耗理论模型能够正确反映实验曲线的变化趋势, 可依据模型对钻具的功耗进行预估。

The authors have declared that no competing interests exist.

参考文献
[1] 欧阳自远. 翱翔九天[M]. 上海: 上海科技教育出版社, 2007: 151-167. [本文引用:1]
[2] Yoseph B C, Zacny K. Drilling in Extreme Environments-Penetration and Sampling on Earth and other Planets[M]. Berlin: Deutsche National Bibliothek, 2009. [本文引用:1]
[3] Badescu M, Stroescu S, Sherrit S, et al. Rotary hammer ultrasonic/sonic drill system[C]∥IEEE International Conference on Robotics and Automation, Pasadena, USA, 2008. [本文引用:1]
[4] Marchesi M. Comet sample acquisition for ROSETTA land er mission[C]∥Proceedings of the 9th European Space Mechanisms and Tribology Symposium, Noordwijk, Netherland s, 2001. [本文引用:1]
[5] 丁希仑, 李可佳, 尹忠旺. 面向月壤采集的多杆深层采样器[J]. 宇航学报, 2009, 30(3): 1190-1195.
Ding Xi-lun, Li Ke-jia, Yin Zhong-wang. Multi-rod deep driller for lunar subsurface sampling[J]. Journal of Astronautics, 2009, 30(3): 1190-1195. [本文引用:1]
[6] Glass B J, McKay C, Thompson S. Automated mars drilling for icebreaker[C]∥IEEE Areospace Conference, Montana, USA, 2011. [本文引用:1]
[7] 田野, 邓宗全, 唐德威, 等. 月壤钻探采样装置中的钻杆结构参数优化设计及模拟试验[J]. 机械工程学报, 2012, 48(23): 10-15.
Tian Ye, Deng Zong-quan, Tang De-wei, et al. Structure parameters optimization and simulation experiment of auger in lunar soil drill-sampling device[J]. Chinese Journal of Mechanical Engineering, 2012, 48(23): 10-15. [本文引用:2]
[8] 邓宗全, 田野, 唐德威, 等. 用于地外星体探测的一种新结构取心钻头研究[J]. 机械工程学报, 2013, 49(19): 45-56.
Deng Zong-quan, Tian Ye, Tang De-wei, et al. Research on new structure coring bit for extraterrestrial bodies exploration[J]. Chinese Journal of Mechanical Engineering, 2013, 49(19): 45-56. [本文引用:2]
[9] Deng Z Q, Tian Y, Tang D W, et al. A new planetary exploration coring bit design and its performance tests research[C]∥IEEE International Conference on Information and Automation, Yinchuan, China, 2013. [本文引用:2]
[10] 郑永春, 欧阳自远, 王世杰, 等. 月壤的物理和机械性质[J]. 矿物岩石, 2004, 24(4): 14-19.
Zheng Yong-chun, Ou-yang Zi-yuan, Wang Shi-jie, et al. Physical and mechanical properties of lunar regolith[J]. Journal of Mineralogy and Petrology, 2004, 24(4): 14-19. [本文引用:1]
[11] 郭志建. 吊夯式模拟月壤制备装置研制及试验研究[D]. 哈尔滨: 哈尔滨工业大学, 2012.
Guo Zhi-jian. Development of the hoist-release preparing device of lunar stimulant soil and experimental research[D]. Harbin: Harbin Institute of Technology, 2012. [本文引用:1]
[12] 丁亮. 月/星球车轮地作用地面力学模型及其应用研究[D]. 哈尔滨: 哈尔滨工业大学, 2010.
Ding Liang. Wheel-soil interaction terramechanics for lunar/planetary exploration rovers: modeling and application[D]. Harbin : Harbin Institute of Technology, 2010. [本文引用:1]
[13] 丁亮, 高海波, 邓宗全, 等. 基于应力分布的月球车轮地相互作用地面力学模型[J]. 机械工程学报, 2009, 45(7): 49-52.
Ding Liang, Gao Hai-bo, Deng Zong-quan, et al. Terramechanics model for wheel-terrain interaction of lunar rover based on stress distribution[J]. Chinese Journal of Mechanical Engineering, 2009, 45(7): 49-52. [本文引用:1]
[14] 王清川. 月壤钻取采样参数测试平台的研制[D]. 哈尔滨: 哈尔滨工业大学机电工程学院, 2012.
Wang Qing-chun. Development of the lunar soil drilling test bed[D]. Harbin: School of Mechatronics Engineering, Harbin Institute of Technology, 2012. [本文引用:1]
[15] 肖洪. 深层月壤取心钻头构型设计及其力载特性研究[D]. 哈尔滨: 哈尔滨工业大学机电工程学院, 2013.
Xiao Hong. Research of structure design of deep lunar soil coring bit and characteristics of load[D]. Harbin: School of Mechatronics Engineering, Harbin Institute of Technology, 2013. [本文引用:1]