分布式位移加载方式拉伸成形三维曲面件的数值模拟

引用本文

杨振, 蔡中义, 李明哲. 分布式位移加载方式拉伸成形三维曲面件的数值模拟. 吉林大学学报: 工学版, 2016, 46(1): 199-204
YANG Zhen, CAI Zhong-yi, LI Ming-zhe. Stretch forming of three-dimensional sheet metal part by distributed displacement loading method. Journal of Jilin University Engineering and Technology Edition, 2016, 46(1): 199-204 复制到剪切板

Permissions

分布式位移加载方式拉伸成形三维曲面件的数值模拟

杨振, 蔡中义, 李明哲

吉林大学辊锻工艺研究所,长春 130022

蔡中义(1963-),男,教授,博士生导师.研究方向:板料柔性成形,有限元理论.E-mail:czy@jlu.edu.cn

作者简介:杨振(1990-),男,博士研究生.研究方向:板料柔性成形.E-mail:yangzhen0517@163.com

基金:国家自然科学基金项目(51575231)

摘要

建立了分布式位移加载方式拉伸成形的有限元模型,对该方法成形三维曲面进行位移加载路径设计。对球形件和鞍形件的成形过程进行了数值模拟,对比分析离散加载点数以及加载时间步数对于成形件应力应变分布的影响。结果表明,离散加载点数越多,应变分布越均匀,成形质量越好;加载时间步越多,板料成形区应力变化幅度越小,应力应变分布越均匀,成形效果越好,但是当加载时间步到达一定数值后,随着加载时间步的增加,成形件应力应变分布变化不明显。最后通过实验验证这种拉伸成形方法的可行性。

关键词: 材料合成与加工工艺; 拉伸成形; 分布式位移加载; 加载路径; 数值模拟

中图分类号:TG306 文献标志码:A 文章编号:1671-5497(2016)01-0199-06

Stretch forming of three-dimensional sheet metal part by distributed displacement loading method

YANG Zhen, CAI Zhong-yi, LI Ming-zhe

Rolling Forging Institute,Jilin University, Changchun 130022,China

Abstract

A finite element model of stretch forming was established based on distributed displacement loading and the displacement loading trajectory of forming the three-dimensional surface was designed. Spherical parts and saddle parts were selected for simulation, the effects of the number of discrete loading points and loading time-steps on the stress and strain distribution on the formed part were analyzed comparatively. Results show that the more discrete loading points, the higher uniformity of the strain distribution and the better forming quality; and the more loading time-steps, the smaller variation of the stress magnitude and the better forming quality. However, when the loading time-step reaches a certain value, there were no obvious changes in the stress and strain distributions with further increase in the loading time-step. Experiment results demonstrate to feasibility of proposed displacement loading method.

Keyword: materials synthesis and processing technology; stretch forming; distributed displacement loading; loading trajectory; numerical simulation

Show Figures

拉伸成形^[1]是板类三维曲面件成形的一种重要方式, 拉伸成形件回弹小, 应变分布比较均匀^[2], 在高速列车及航空制造领域得到广泛应用。传统的拉伸成形设备由于采用整体夹钳, 板材在成形过程中容易产生应力集中、起皱、拉裂、不完全贴膜等缺陷^[3], 此外, 传统拉伸成形的控制系统复杂、调试周期长、对生产经验的依赖性较强、成形质量不稳定^{[4, 5, 6]}。多夹钳柔性拉形机^[7]改变了整体夹钳的加载模式, 实现了离散加载, 但是这种拉形机采用力加载控制成形过程。文献[8, 9]提出了一种分布式位移加载的三维曲面拉伸成形方法, 这种拉伸成形方法通过实时控制板料两端离散点的加载路径, 使成形过程中板料变形更加均匀, 改善了贴膜过程, 避免缺陷的产生, 从而获得高质量的三维曲面件。

本文用有限元软件ABAQUS建立分布式位移加载方式拉伸成形的有限元模型, 对离散点的加载轨迹进行设计, 得到离散加载点在成形过程中水平和垂直方向的位移。对球形件及马鞍形件进行数值模拟, 对比分析离散加载点数以及加载时间步数对成形件应力应变分布的影响, 并通过实验验证了本文拉伸成形方法的可行性。

1 位移加载路径设计

分布式位移加载方式成形三维曲面的方法基于离散化的思想, 把位移载荷施加于板料两端的一系列离散点上, 并把加载过程分为多个时间步, 通过控制离散加载点加载轨迹实现拉伸成形过程。由于离散加载点数以及加载时间步数对成形件应力应变分布影响比较大, 因此选择合适的离散加载点数和加载时间步数可以实现板料变形的均匀化, 避免缺陷的产生, 从而得到高质量的成形件, 图1为分布式位移加载拉伸成形装置结构示意图。

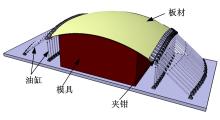	Figure Option View Download New Window
	图1 分布式位移加载拉伸成形装置结构示意图Fig.1 Structure diagram of stretch forming apparatus with distributed displacement loading

对于任意的拉形模具, 设模具型面的方程为F(x, y, z)=0, 垂直于z轴的平面(z=z_i)截得柔性拉伸成形的几何示意图如图2所示, 板料的初始长度为2AB=2l₀, 模具长度为2l_m, 模具型面曲线AD的方程为y=φ (x, z_i), 曲线AD长度为:

$\begin{matrix} s = \int_{0}^{l_{m}} \sqrt[]{1 + {(\frac{dφ (x, z_{i})}{dx})}^{2}} dx (1) \end{matrix}$

	Figure Option View Download New Window
	图2 柔性拉伸成形几何示意图Fig.2 Geometric diagram of flexible stretch forming

在分布式位移加载方式拉伸成形三维曲面过程中, 先把板料横向弯曲成与模具型面接触的柱面, 然后把加载过程分为n个时间步, 在加载过程中纵向纤维伸长率均匀增加, P_j为第j个时间步板料与模具型面曲线AD的切点, 则:

$\begin{matrix} \int_{0}^{x_{P_{j}}} \sqrt[]{1 + {(\frac{dφ (x, z_{i})}{dx})}^{2}} dx = js / n (2) \end{matrix}$

由式(2)可得到P_j点的x坐标 $\begin{matrix} x_{P_{j}} \end{matrix}$ , 则直线P_jQ_j的斜率为:

$\begin{matrix} \begin{matrix} k_{P_{j} Q_{j}} = \frac{dφ (x, z_{i})}{dx}| \underset{x = x_{P_{j}}}{} = - \tan θ_{ij} (3) \\ \tan θ_{ij} = \arctan (- k_{P_{j} Q_{j}}) = \arctan (- \frac{dφ (x, z_{i})}{dx}] \underset{x = x_{P_{j}}}{}) (4) \end{matrix} \end{matrix}$

式中:θ _ij为直线P_jQ_j与水平方向的夹角。因此加载点第j个时间步的位移可以表示如下:

$\begin{matrix} \{\begin{matrix} Δx (t_{j}) = x_{P_{j}} + (l_{0} + Δ l_{j} - js / n) \cos θ_{ij} - l_{0} \\ Δy (t_{j}) = φ (x_{P_{j}}, z_{i}) - (l_{0} + Δ l_{j} - \\ js / n) \sin θ_{ij} - φ (0, z_{i}) \end{matrix} (5) \end{matrix}$

式中:Δ l_j=jδ _il₀/n, δ _i为板材在(z=z_i)截面的延伸率; z_i=(i-0.5)C/f, C为板料1/2宽度, f为板料一侧离散点个数的一半; t_j满足下式:

$\begin{matrix} \begin{matrix} t_{j} = \overset{j}{\sum_{k = 1}} Δ t_{k} (6) \\ \begin{matrix} Δ t_{k} = \\ \max_{1 \leq i \leq f} \{[x_{P_{k}} - x_{P_{k - 1}} + (l_{0} + Δ l_{k} - ks / n) \cos θ_{ik} - \\ (l_{0} + Δ l_{k} - (k - 1) s / n) \cos θ_{ik - 1}]^{2} + \\ [φ (x_{P_{k}}, z_{i}) - φ (x_{P_{k - 1}}, z_{i}) - \\ (l_{0} + Δ l_{k} - ks / n) \sin θ_{ik} - \\ (l_{0} + Δ l_{k - 1} - (k - 1) s / n) \sin θ_{ik - 1}]^{2}}^{\frac{1}{2}} / v \end{matrix} (7) \end{matrix} \end{matrix}$

假设成形过程为拉伸速度为v的匀速运动。

对于一些特殊的三维曲面件如球形件、鞍形件, 在成形过程中加载点第j时间步的位移可表示为:

$\begin{matrix} \{\begin{matrix} Δx (t_{j}) = ρ_{i} \sin θ_{ij} + (l_{0} + Δ l_{j} - ρ_{i} θ_{ij}) \cos θ_{ij} - l_{0} \\ Δy (t_{j}) = ρ_{i} \cos θ_{ij} - (l_{0} + Δ l_{j} - ρ_{i} θ_{ij}) \sin θ_{ij} - ρ_{i} \end{matrix} (8) \end{matrix}$

其中对于球形件ρ _i= $\begin{matrix} \sqrt[]{R^{2} - {z_{i}}^{2}} \end{matrix}$ , 对于鞍形件ρ _i=2R- $\begin{matrix} \sqrt[]{R^{2} - {z_{i}}^{2}} \end{matrix}$ , R为球形件和鞍形件的半径; θ _ij=jθ _i/n, θ _i=arcsin(l_m/ρ _i), 假设在成形过程中球形件横向边缘的纵向纤维长度不变, 则纵向纤维的伸长量为:

$\begin{matrix} \begin{matrix} Δl (z) = ω (\sqrt[]{R^{2} - z^{2}} - \sqrt[]{R^{2} - C^{2}}) (9) \\ ω = \arcsin (l_{0} / \sqrt[]{R^{2} - C^{2}}) (10) \end{matrix} \end{matrix}$

式中:Δ l_j=jΔ l(z_i)/n; 对于鞍形件假设中心线的纵向纤维长度不变, 则纵线纤维的伸长量为:

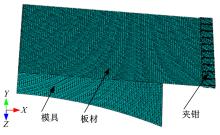
$\begin{matrix} Δl (z) = ω (2 R - \sqrt[]{R^{2} - z^{2}}) (11) \end{matrix}$

2 加载点数对应变分布的影响

球形件和鞍形件是两种常见的三维曲面件, 本文以球形件为例建立有限元模型。模具型面的半径为500 mm, 长度和宽度均为300 mm, 板料为1 mm厚、400 mm长、300 mm宽的2024-O铝合金材料, 其主要力学性能参数为:密度为2720 kg/m³, 弹性模量为40.6 MPa, 泊松比为0.33, 屈服强度为75.3 MPa, 抗拉强度为191 MPa。考虑到球面的对称性, 建立1/4有限元模型, 如图3所示。本文采用动态显示算法ABAQUS/Explicit模拟分布式位移加载成形球形件以及鞍形件的过程, 其中模具和夹钳采用解析刚体模型, 采用R3D4单元划分网格; 板料采用弹塑性模型, 采用S4R单元划分网格。

	Figure Option View Download New Window
	图3 1/4有限元模型Fig.3 A quarter of FE model

对球形件在不同加载点时进行拉伸成形数值模拟, 本文选取加载点数分别为8、16、20。图4为不同加载点数时成形的球形件在x方向的应变分布。由图4可以看出, 离散加载点越多, 板料在成形过程中受力越均衡, 应变分布越均匀。

	Figure Option View Download New Window
	图4 不同离散加载点时球形件在x方向的应变分布Fig.4 x-direction strain distribution of spherical part with different discrete loading points

OC线为板料纵向的对称轴线, OD线为板料横向的对称轴线。不同加载点数时得到的球形件沿OC和OD方向的拉伸应变分布见图5。由图5(a)可知, 球形件沿OC方向的应变变化幅度在8个加载点时最大, 16个点时次之, 20个点时最小。加载点越多应变曲线坡度越小, 应变分布越均匀, 成形效果越好。由图5(b)可得出, 不同离散加载点成形的球形件沿OD方向应变均是逐渐递减的, 加载点越多, 沿OD方向的最大应变越小, 应变变化幅度越小, 分布越均匀。

	Figure Option View Download New Window
	图5 不同离散加载点时球形件沿OC和 OD方向的拉伸应变Fig.5 Stretching strain of spherical part with different discrete loading points along OC and OD

3 加载时间步对应力应变分布的影响

为了分析成形过程中加载时间步对成形件应力应变分布的影响, 分别取加载时间步为1、5、10进行数值模拟。通过对比分析不同加载时间步成形的球形件的应力应变分布以及成形球形件沿纵向对称轴线以及横向对称轴线的应力应变分布, 进而探究加载时间步对应力应变分布的影响作用。

3.1 加载时间步对应力分布的影响

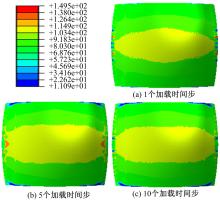
不同加载时间步条件下得到的球形件沿x方向的应力分布如图6所示。由应力分布图可看出, 加载时间步为1时的板料应力分布不均匀, 加载时间步为5和10时的板料成形区应力分布状况基本一致, 分布比较均匀, 只有在过渡区有细微的差别。说明成形过程加载时间步越多, 成形件的应力分布越均匀, 成形效果越好, 但是当加载时间步到达一定数值后, 随着加载时间步的增加, 成形件应力分布变化不明显。

	Figure Option View Download New Window
	图6 不同加载时间步时球形件在x方向的应力分布Fig.6 x-direction stress distribution of spherical part with different loading time-steps

3.2 加载时间步对应变分布的影响

不同加载时间步条件下得到的球形件沿x方向的应变分布如图7所示。由图7可以看出, 1个加载时间步时的球形件应变分布最不均匀, 5个和10个加载时间步时的成形件应变分布比较均匀, 应变分布差别不明显。

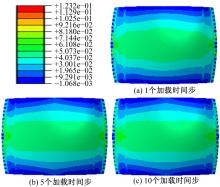	Figure Option View Download New Window
	图7 不同加载时间步时球形件在x方向的应变分布Fig.7 x-direction strain distribution of spherical part with different loading time-steps

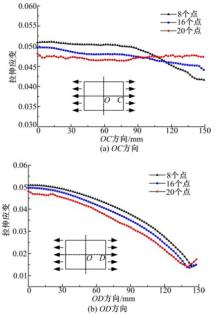
不同加载时间步条件下得到的球形件沿OC和OD方向的拉伸应变分布如图8所示。由图8(a)可知, 成形球形件沿OC方向应变变化都比较平缓, 加载时间步越多, 应变变化幅度越小, 分布更加均匀。由图8(b)可以看出, 沿OD方向应变由板料中部向板料边缘呈递减趋势, 1个加载时间步时应变曲线波动比较明显, 5个和10个加载时间步时应变曲线比较平滑, 应变分布基本一致, 成形效果比较好。与1个加载时间步时相比, 加载时间步为5时沿OC方向的应变变化减小42.8%, 沿OD方向应变变化减小18.4%; 加载时间步为10时沿OC方向的应变变化减小77.9%, 沿OD方向应变变化减小27.4%。

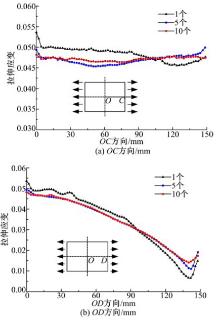	Figure Option View Download New Window
	图8 不同加载时间步时球形件沿OC和 OD方向的拉伸应变Fig.8 Stretching strain of spherical part with different loading time-steps along OC and OD

综合上述的对比分析结果, 选取20个离散加载点、10个加载时间步作为加载条件, 对鞍形件成形进行数值模拟得到的应力应变分布如图9所示。由应力及应变图可以看出, 成形件在拉伸成形过程中受力比较均衡, 应力应变分布比较均匀, 贴膜良好, 成形质量比较高。

	Figure Option View Download New Window
	图9 鞍形件在x方向的应力应变分布Fig.9 x-direction stress and strain distribution of saddle part

为了验证分布式位移加载方式拉伸成形三维曲面方法的可行性, 本文采用长为400 mm、宽为300 mm、厚度为1 mm、摩擦因数为0.1的2024-O为实验材料。由图10可以看出实验件的有效成形区表面光滑, 没有起皱等缺陷, 成形质量比较好。

	Figure Option View Download New Window
	图10 球形试验件Fig.10 Experiment diagram spherical part

4 结论

(1)离散加载点数越多, 板料在拉伸成形过程中受力越均衡, 成形件应变变化幅度越小, 分布越均匀, 成形效果越好。

(2)在板料成形过程中加载时间步越多, 成形件的应力分布越均匀, 成形质量越高, 但是当加载时间步达到一定值后, 随着时间步的增加, 成形件的应力分布趋于稳定, 变化不明显。

(3)加载时间步越多, 成形件应变变化幅度越小, 应变变化越平稳, 分布也越均匀, 成形质量越高。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	翟平, 林兆荣. 飞机钣金成形原理与工艺[M]. 西安: 西北工业大学出版社, 1995. [本文引用:1]
[2]	Cai Zhong-yi, Wang Shao-hui, Xu Xu-dong, et al. Numerical simulation for the multi-point stretch formingprocess of sheet metal[J]. Journal of Materials Processing Technology, 2009, 209(1): 396-407. [本文引用:1]
[3]	侯红亮, 余肖放, 曾元松. 国内航空钣金装备技术现状与发展[J]. 航空制造技术, 2009(1): 34-39. Hou Hong-liang, Yu Xiao-fang, Zeng Yuan-song. Current and development status of sheet metal equipment and technology in Chinese aviation industry[J]. Aeronautical Manufacturing Technology, 2009(1): 34-39. [本文引用:1]
[4]	冯朋晓, 李明哲, 付文智. 高柔性多夹钳拉形机的结构设计[J]. 锻压装备与制造技术, 2010, 45(5): 21-25. Feng Peng-xiao, Li Ming-zhe, Fu Wen-zhi. Structure d-esign of the high-flex stretch-forming machine with m-ultiple clamps[J]. China Metal Forming Equipment & Manufacturing Technology, 2010, 45(5): 21-25. [本文引用:1]
[5]	彭赫力, 李明哲, 付文智, 等. 柔性离散夹钳拉形工艺的数值模拟[J]. 吉林大学学报: 工学版, 2012, 42(5): 660-664. Peng He-li, Li Ming-zhe, Fu Wen-zhi, et al. Numerical simulation of flexible discrete clamp stretch forming process[J]. Journal of Jilin University(Engineering and Technology Edition), 2012, 42(5): 660-664. [本文引用:1]
[6]	周朝晖, 蔡中义, 李明哲. 多点模具的拉形工艺及其数值模拟[J]. 吉林大学学报: 工学版, 2005, 35(3): 287-291. Zhou Zhao-hui, Cai Zhong-yi, Li Ming-zhe. Stretching process based on multi-point die and its numerical simulation[J]. Journal of Jilin University(Engineering and Technology Edition), 2005, 35(3): 287-291. [本文引用:1]
[7]	陈雪, 李明哲, 付文智. 球形件多钳式柔性拉形的数值模拟[J]. 锻压技术, 2010, 35(4): 32-36. Chen Xue, Li Ming-zhe, Fu Wen-zhi. Numerical simulation of multiple grippers flexible stretch forming for spherical part[J]. Forging and Stamping Technology, 2010, 35(4): 32-36. [本文引用:1]
[8]	Cai Zhong-yi, Wang Mi, Yang Zhen, et al. Numerical investigation on the process of stretch-forming based on discretely loading for spherical sheet metal parts[J]. Advanced Materials Research, 2013, 816-817: 682-685. [本文引用:1]
[9]	Cai Zhong-yi, Wang Mi, Che Chao-jie. A new stretch-forming process based on loading at discrete points and its numerical investigation[J]. Applied Mechanics and Materials, 2013, 423-426: 737-740. [本文引用:1]

1995

0.0

... 拉伸成形^[1]是板类三维曲面件成形的一种重要方式,拉伸成形件回弹小,应变分布比较均匀^[2],在高速列车及航空制造领域得到广泛应用 ...

2009

0.0

... 拉伸成形^[1]是板类三维曲面件成形的一种重要方式,拉伸成形件回弹小,应变分布比较均匀^[2],在高速列车及航空制造领域得到广泛应用 ...

0.0

... 传统的拉伸成形设备由于采用整体夹钳,板材在成形过程中容易产生应力集中、起皱、拉裂、不完全贴膜等缺陷^[3],此外,传统拉伸成形的控制系统复杂、调试周期长、对生产经验的依赖性较强、成形质量不稳定^[4,5,6] ...

2010

0.0

2012

0.0

2005

0.0

. 2005, 35(3):287-291

Stretching process based on multi-point die and its numerical simulation

多点模具的拉形工艺及其数值模拟

Zhou Zhao-hui , Cai Zhong-yi , Li Ming-zhe.

周朝晖, 蔡中义, 李明哲

为检验多点模具拉形工艺的可行性，采用显式有限元软件对抛物柱面与马鞍面件的拉形过程进行了数值模拟，并与采用整体模具的拉形效果进行了比较。数值模拟结果表明：使用多点模具直接进行蒙皮拉形，成形件表面将出现压痕。为抑制压痕，必须在多点模具与板料之间放置弹性垫层。弹性垫能够有效地分散多点模具冲头的集中载荷。当弹性垫较薄时，成形件表面仍有压痕出现，当弹性垫厚度达到8 mm时，压痕被消除，成形表面光滑，与整体模具的成形结果非常接近。实验表明：只要采用合适的弹性垫，多点模具可应用于实际拉形工艺。

2010

0.0

... 多夹钳柔性拉形机^[7]改变了整体夹钳的加载模式,实现了离散加载,但是这种拉形机采用力加载控制成形过程 ...

2013

0.0

2013

0.0