基于响应面的封头冲压成形工艺多目标优化

引用本文

周杰, 罗艳, 王珣, 王辉, 李洋, 陶亚平. 基于响应面的封头冲压成形工艺多目标优化. 吉林大学学报: 工学版, 2016, 46(1): 205-212
ZHOU Jie, LUO Yan, WANG Xun, WANG Hui, LI Yang, TAO Ya-ping. Multi-objective optimization of stamping forming process of head based on response surface model. Journal of Jilin University Engineering and Technology Edition, 2016, 46(1): 205-212 复制到剪切板

Permissions

基于响应面的封头冲压成形工艺多目标优化

周杰, 罗艳, 王珣, 王辉, 李洋, 陶亚平

重庆大学材料科学与工程学院,重庆 400044

作者简介:周杰(1965-),男,教授,博士生导师.研究方向:冲压关键技术,材料成形数值模拟仿真与优化.E-mail:luoyan636@163.com

基金:国家自然科学基金项目(51275543)

摘要

针对某封头加工厂在生产某型号封头零件时出现的起皱鼓包、厚度分布不均匀以及回弹变形严重的缺陷,提出一种新型的优化成形工艺方案。以减少起皱及鼓包现象、增大厚度均匀区、减小回弹变形量为优化目标,并以凸凹模间隙、凹模圆角半径、拉延筋高度以及拉延筋相对位置为优化因素,采用Matlab与Design-Expert软件相结合的方式进行响应面(RSM)拟合建模分析,得到3个目标量的二阶响应面模型,并验证了所建立的响应面模型的准确性,其误差范围小于7.4%,可用于后续优化。生产实践结果表明通过多目标优化后的封头成形工艺可以获得表面质量好、形状误差小、尺寸精度高的产品。

关键词: 铸造工艺与设备; 冲压成形; 封头; 响应面法; 多目标优化; 有限元模拟

中图分类号:TG386.41 文献标志码:A 文章编号:1671-5497(2016)01-0205-08

Multi-objective optimization of stamping forming process of head based on response surface model

ZHOU Jie, LUO Yan, WANG Xun, WANG Hui, LI Yang, TAO Ya-ping

College of Materials Science and Engineering, Chongqing University, Chongqing 400044, China

Abstract

In the forming process of heads the defects of wrinkling, swelling, nonuniformity of the thickness, and springback deformation occurred in a certain factory. To solve these problems, optimized scheme is proposed. The objectives of this scheme are reducing the swelling, enlarging the region of uniform thickness, and decreasing the springback deformation. The optimizing factors include the clearance between the punch and die, the matrix radius, the height of drawbead and the relative position of the drawbead. The combination of software of Matlab and Design-Expert was adopted to conduct fitting and modeling analysis of the Response Surface Model (RSM). A second-order RSM with three objective values was obtained. The accuracy of the obtained RSM was verified and the error margin was less than 7.4%, which was available for subsequent optimizations. The actual production results show that heads with good surface finish, small shape error and high dimension precision can be produced by the application of the proposed multi-objective optimization scheme of forming process.

Keyword: casting process and equipment; stamping; heads; response surface method; multi-objective optimization; finite element simulation

Show Figures

0 引言

大型封头作为容器装备的重要受力部件, 广泛用于铁路、石油化工、压力容器、核工业和食品加工等行业, 其质量对装备运行安全起着至关重要的作用。国内现行的主要工艺路线是将拼焊板坯料进行多次冲压成形制造, 通过生产实践发现椭圆封头成形工艺参数对封头成形质量起着至关重要的作用。

针对椭圆封头冲压成形问题国内研究学者进行了一系列的研究工作, 包括对封头拉延成形工艺的研究分析, 对大型椭圆封头成形加工的坯料尺寸、成形载荷的计算, 对封头成形冲压模具结构的设计, 以及采用有限元仿真模拟软件对封头冷冲压成形的分析^[1]。国外学者Chakrabarty、Chao等在对压力容器封头进行受力分析的基础上, 对半球形零件的模具冲压成型进行试验研究^{[2, 3]}。Fiorentino等^[4]对金属板料旋压时的受力、成形精度开展了试验研究, Durante^[5]分析了成形辊旋压对旋压成形的影响。大量的研究分析与实际使用数据表明, 封头主要失效形式包括起皱鼓包明显、壁部减薄厚度变化不均匀、回弹变形严重。针对椭圆封头冲压成形多数研究基本上从单因素方面单目标来分析预测成形过程^{[6, 7]}。实际上, 封头起皱、减薄率不均匀以及回弹变形量大等缺陷之间存在着耦合关系, 本文针对某封头制造厂生产的某型号奥氏体不锈钢的椭圆封头热冲压成形工艺中出现的起皱鼓包缺陷、厚度变化不均匀、回弹变形量过大的问题, 采用协同优化的响应面法作为优化方法并使用Matlab进行数据处理分析。经实践生产验证, 能够得到成形表面质量好、厚度减薄均匀以及回弹变形量合理的封头件^[8]。

1 拉深工艺分析及优化参数建立

1.1 封头拉深失稳分析

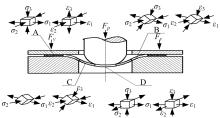
封头拉深成形时各部分的受力情况与应力状态不同, 变形趋势和失稳方式也不同。坯料在凸模冲压力F_p和压边力F_y作用下, 包含4个主要变形区域:凸缘面A、凹模入口圆角区B、悬空区C和椭球形区D。图1为各变形区的应力应变情况, 其中凸缘面A、凹模入口圆角区B和悬空区C处切向应变ε ₂的绝对值最大, 易产生起皱缺陷。椭球形区D处材料承受较大的径向拉应力σ ₁和切向拉应力σ ₂, 成为整个封头件胀形变形区, 该处材料有变薄趋势^[3]。因此, 封头在拉深成形时应力应变是复杂的, 时刻在变化的, 封头的壁厚也是不均匀的, 且在压应力的作用下会产生“ 起皱鼓包” 缺陷、而不均匀不完全的变形增大了回弹变形的不可控性。基于对封头拉深失稳分析可知, 在材料特性和冲压件几何形状一定的情况下为了将成形缺陷控制为最小, 通过多目标优化方法, 选取待优化目标为主要控制参数, 建立代理模型寻求最优工艺参数组合。

	Figure Option View Download New Window
	图1 封头成形各变形区应力和应变图Fig.1 Stress and strain diagrams in deformation zone of heads during forming

本文选取凸凹模间隙t、凹模入口圆角半径R、拉延筋高度H、拉延筋相对位置L(L=(r_坯-r_凸)/r_凹)为优化变量, 以起皱情况、厚度不均匀程度、回弹变形量为优化目标来提高封头件成形质量。凸凹模间隙t减小时坯料与模具间的摩擦力增大, 而摩擦力在一般情况下可以增大变形区的拉应力σ ₁, 使板料内外应力趋于一致, 减小回弹值。但间隙过小时, 凸缘区的材料通过它时矫直与变形的阻力增加, 与模具表面摩擦增大, 使得径向拉应力σ ₁过大, 零件变薄严重。过小的凹模圆角半径R易划伤通过该处的坯料, 而当半径R过大时, 拉深初期坯料不与模具表面接触的宽度加大, 这部分材料不受压边圈作用, 即σ ₃=0, 容易起皱。且坯料滑过过大的凹模圆角半径时流动阻力减小, 相应的径向拉应力σ ₁减小, 材料塑性变形不充分, 从而导致回弹变形量增大。如前所述, 封头件在拉深成形时凸缘区起皱趋势明显, 因此需要合适的径向拉应力σ ₁, 而σ ₁主要是由冲裁力、凸缘区坯料的变形抗力、压边圈作用力产生, 拉延筋的设置能增大压边圈的阻力, 增大σ ₁从而增大板料的塑性变形, 减小回弹变形量, 并且拉延筋能控制板料的变形大小和分布, 促使零件厚度分布均匀。

1.2 拉深工艺优化参数建立

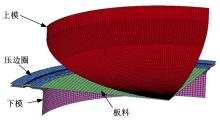
本文所研究的Dynaform仿真模型是基于工厂实际的工艺参数建立起来的, 模型结构如图2所示。数值模拟的相关参数设置:封头材料为1Cr18Ni9Ti, 该种材料在Dynaform材料库中的牌号为AISI321, 材料本构方程如式(1)所示:

$\begin{matrix} \bar{σ} = 1.07287 {\bar{ε}}^{0.192647} {\overset{\cdot}{\bar{ε}}}^{1.52126} + 81.82 (1) \end{matrix}$

该材料杨氏模量为210 GPa, 泊松比为0.28, 硬化指数为0.425, 强化系数为520, 厚向异性系数为1.19。坯料半径r_坯=1875 mm, 凸模半径r_凸=1497.5 mm, 凹模半径r_凹=t+r_凸, 其中t为凸凹模间隙。凸凹模压边闭合时凸模速度为120 mm/s, 拉深成形时凸模速度为15 mm/s, 压边圈压边力为5000 kN, 坯料与模具的摩擦因数为0.125, 冲压成形温度为1000 ℃。其余参量根据文献[1, 2]分别固定为其最佳水平。

	Figure Option View Download New Window
	图2 封头成形有限元模型Fig.2 Finite element model of heads during forming

2 基于响应面方法优化

2.1 目标函数的建立

目标函数是量化具体成形失稳方式的评判准则, 如上所述本文将起皱、厚度不均匀程度和回弹变形量作为优化目标。根据Hillmann等^[9]对起皱成形极限曲线的定义, 构建起皱D_w、厚度不均匀D_t、平均回弹变形量D_s相应的目标函数如下:

起皱评判函数D_w为:

$\begin{matrix} D_{w} = \{\begin{matrix} \overset{k}{\sum_{i = 1}} (ϕ ({ε_{2}}^{i}) - {ε_{1}}^{i})^{2}, {ε_{1}}^{i} < ϕ ({ε_{2}}^{i}) \\ 0, {ε_{1}}^{i} \geq ϕ ({ε_{2}}^{i}) \end{matrix} (2) \end{matrix}$

厚度偏差目标函数D_t为:

$\begin{matrix} D_{t} = \overset{k}{\sum_{i = 1}} {(\frac{t_{i}}{t_{0}} - 1)}^{4} (3) \end{matrix}$

平均回弹量目标函数D_s为:

$\begin{matrix} D_{s} = (\overset{k}{\sum_{i = 1}} \sqrt[]{d^{2}}) / k (4) \end{matrix}$

式(2)(3)(4)中:ε ₁为主应变; ε ₂为次应变; k为被测单元数; i为单元编号; t₀为初始板料厚度; t_i为最终板料厚度; d为各个单元回弹变形量。

2.2 响应面的优化试验设计

响应面法的使用必须先确定合理的因素以及相应的水平参数^[10]。令凸凹模间隙t、凹模圆角半径R、拉延筋高度H、拉延筋相对位置L分别为优化变量X₁、X₂、X₃、X₄。起皱目标函数D_w、厚度不均匀目标函数D_t、平均回弹变形量目标函数D_s分别为Y₁、Y₂、Y₃, 其中Y₁、Y₂、Y₃越小越好。本文在生产实践的基础上借助数值模拟采用最陡坡实验确定4个因素的合理范围, 如表1所示。

表1 最陡爬坡试验设计及结果 Table 1 Steepest ascent design and results

由表1可知, 起皱目标最小值出现在组合2、3之中; 厚度不均匀、平均回弹变形量目标最小值均出现在第3组。因此, 成形最优参数组合在第3组附近, 故将响应面实验的中心点设置为(11, 45, 40, 0.4)。

本次响应面法试验有优化变量4个, 优化目标函数3个, 因此二阶响应面模型的回归系数共有q= $\begin{matrix} C_{4 + 2}^{2} \end{matrix}$ =15。为了得到合理的回归方程, 选择最陡坡试验和中心复合设计(Center composite design, CCD)相结合来设计试验, 每个因子所取的水平数为5个^[11]。借助专业的设计软件Design-Expert v8.0来设计, 以完成后续的响应面分析。在前面分析的基础上进行了4因素5水平的中心复合设计, 共进行30次试验。因素水平如表2所示, 部分实验方案及试验结果如表3所示。通过编写Matlab语言程序对有限元求解后的dynain关键字文件进行相关计算, 从而得到输出的相应面值。

表2 优化因素取值水平 Table 2 Levels of variable values

表3 中心复合试验方案及试验结果 Table 3 Central composite design and results

2.3 响应面模型构建与结果分析

采用不完全二阶模型建立3个目标响应Y关于设计变量参数的预测模型。对于四因素五水平多项式不完全模型为:

$\begin{matrix} y = a_{0} + \overset{n}{\sum_{i = 1}} a_{i} x_{i} + \overset{n}{\sum_{i = 1}} a_{ii} x_{i}^{2} + \overset{n - 1}{\sum_{i = 1}} \overset{n}{\sum_{j > 1}} a_{ij} x_{i} x_{j} + ε (5) \end{matrix}$

根据式(5), 应用最小二乘法对表3中的数据进行回归分析, 分别得到Y₁、Y₂、Y₃的响应函数如下:

Y₁=171.92321-23.95411X₁-1.15335X₂-

0.9912X₃+22.79830X₄+0.030666X₁X₂+

0.024352X₁X₃-1.79668X₁X₄-1.83290X₂X₃-0.12843X₂X₄-0.22829X₃X₄+1.0255 $\begin{matrix} {X_{1}}^{2} \end{matrix}$ +

0.010660 $\begin{matrix} {X_{2}}^{2} \end{matrix}$ +0.011186 $\begin{matrix} {X_{3}}^{2} \end{matrix}$ +14.07695 $\begin{matrix} {X_{4}}^{2} \end{matrix}$ (6)

Y₂=718.80282-90.75706X₁-4.31284X₂-

7.39749X₃+107.45335X₄-0.079833X₁X₂+

0.28068X₁X₃-7.3284X₁X₄+2.22709X₂X₃-

0.29882X₂X₄-0.62499X₃X₄+3.92744 $\begin{matrix} {X_{1}}^{2} \end{matrix}$ +

0.057666 $\begin{matrix} {X_{2}}^{2} \end{matrix}$ +0.058700 $\begin{matrix} {X_{3}}^{2} \end{matrix}$ +14.36480 $\begin{matrix} {X_{4}}^{2} \end{matrix}$ (7)

Y₃=329.53689-40.21211X₁-1.95687X₂-

3.79947X₃+48.92202X₄-0.051260X₁X₂+

0.15308X₁X₃-3.81925X₁X₄+1.62150X₂X₃-

0.030675X₂X₄-0.29899X₃X₄+1.7340 $\begin{matrix} {X_{1}}^{2} \end{matrix}$ +

0.027182 $\begin{matrix} {X_{2}}^{2} \end{matrix}$ +0.028452 $\begin{matrix} {X_{3}}^{2} \end{matrix}$ +7.78518 $\begin{matrix} {X_{4}}^{2} \end{matrix}$ (8)

为了验证所建的响应面模型是否能真正反映响应面与设计因素间的统计规律, 对式(6)(7)(8)分别进行方差分析, 由其F值检验响应模型的显著性, 当P(概率)(> F(显著性))的值小于0.05时, 即认为该指标是显著的; 而P(> F)的值小于0.01时, 即认为该指标是高度显著^[12]。由表4、表5、表6可知3个模型对应的“ P(> F)” 值依次为0.0001、0.0006、0.0006, 其值均远小于0.01, 说明3种模型皆是高度显著的。因此, Y₁、Y₂、Y₃的最优响应模型均为二次方模型。此外, 还可通过R²和R_adj进一步检验模型的可靠性, 一般情况下认为R²和R_adj值越大, 则回归模型的拟合精度越高^[13]。由表7可知, 3个模型R²值分别为92.33%、85.24%、85.34%, 说明该模型具有很高的预测精度。综上所述, 3个预测模型均能较好地描述所提出的目标量Y₁、Y₂、Y₃关于设计变量X₁、X₂、X₃、X₄的响应, 并能获得很高的预测精度, 可用于后续工艺优化。

表4 方差分析(起皱目标) Table 4 Variance analysis(wrinkle value)

来源	平方和	自由度	均方值	F值	P> F	结果
模型	13.79	14	0.98	12.91	< 0.0001	显著
X₁	0.36	1	0.36	4.65	0.0476	显著
X₂	0.21	1	0.21	2.76	0.1176	显著
X₃	3.308× 10^-3	1	3.308× 10^-3	0.043	0.8379	显著
X₄	0.36	1	0.36	4.75	0.0456	显著
X₁X₂	0.094	1	0.094	1.23	0.2845	显著
X₁X₃	0.059	1	0.059	0.78	0.3920	显著
X₁X₄	0.52	1	0.52	6.77	0.0200	显著
X₂X₃	0.034	1	0.034	0.44	0.5171	显著
X₂X₄	0.26	1	0.26	3.46	0.0827	显著
X₃X₄	0.83	1	0.83	10.93	0.0048	显著
$\begin{matrix} {X_{1}}^{2} \end{matrix}$	1.80	1	1.80	23.62	0.0002	显著
$\begin{matrix} {X_{2}}^{2} \end{matrix}$	1.95	1	1.95	25.53	0.0001	显著
$\begin{matrix} {X_{3}}^{2} \end{matrix}$	2.14	1	2.14	28.11	< 0.0001	显著
$\begin{matrix} {X_{4}}^{2} \end{matrix}$	8.70	1	8.70	113.95	< 0.0001	显著
残差	1.14	15	0.076	-	-
失拟项	1.14	10	0.11	-	-
标准差	0.000	5	0.000	-	-
总模型	14.93	29	-	-	-

表4 方差分析(起皱目标) Table 4 Variance analysis(wrinkle value)

表5 方差分析(厚度不均匀目标) Table 5 Variance analysis(thickness nonuniformity value)

来源	平方和	自由度	均方值	F值	P> F	结果
模型	172.69	14	12.34	6.19	0.0006	显著
X₁	0.74	1	0.74	0.37	0.5526	显著
X₂	0.59	1	0.59	0.30	0.5930	显著
X₃	33.49	1	33.49	16.81	0.0009	显著
X₄	0.013	1	0.013	6.336× 10^-3	0.9376	显著
X₁X₂	0.64	1	0.64	0.32	0.5801	显著
X₁X₃	7.88	1	7.88	3.95	0.0653	显著
X₁X₄	8.59	1	8.59	4.31	0.0554	显著
X₂X₃	0.050	1	0.050	0.025	0.8767	显著
X₂X₄	1.43	1	1.43	0.72	0.4105	显著
X₃X₄	6.25	1	6.25	3.14	0.0969	显著
$\begin{matrix} {X_{1}}^{2} \end{matrix}$	26.44	1	26.44	13.27	0.0024	显著
$\begin{matrix} {X_{2}}^{2} \end{matrix}$	57.01	1	57.01	28.61	< 0.0001	显著
$\begin{matrix} {X_{3}}^{2} \end{matrix}$	59.07	1	59.07	29.64	< 0.0001	显著
$\begin{matrix} {X_{4}}^{2} \end{matrix}$	9.06	1	9.06	4.54	0.0500	显著
残差	29.89	15	1.99	6.19	-
失拟项	29.89	10	2.99	-	-
标准差	0.000	5	0.000	-	-
总模型	202.58	29	-	-	-

表5 方差分析(厚度不均匀目标) Table 5 Variance analysis(thickness nonuniformity value)

表6 方差分析(回弹变形量目标) Table 6 Variance analysis(rebound value)

来源	平方和	自由度	均方值	F值	P> F	结果
模型	40.33	14	2.88	6.24	0.0006	显著
X₁	0.31	1	0.31	0.67	0.4267	显著
X₂	0.28	1	0.28	0.61	0.4455	显著
X₃	7.80	1	7.80	16.89	0.0009	显著
X₄	0.039	1	0.039	0.084	0.7754	显著
X₁X₂	0.26	1	0.26	0.57	0.4623	显著
X₁X₃	2.34	1	2.34	5.08	0.0397	显著
X₁X₄	2.33	1	2.33	5.05	0.0400	显著
X₂X₃	0.026	1	0.026	0.057	0.8146	显著
X₂X₄	0.015	1	0.015	0.033	0.8591	显著
X₃X₄	1.43	1	1.43	3.10	0.0988	显著
$\begin{matrix} {X_{1}}^{2} \end{matrix}$	5.15	1	5.15	11.16	0.0045	显著
$\begin{matrix} {X_{2}}^{2} \end{matrix}$	12.67	1	12.67	27.43	0.0001	显著
$\begin{matrix} {X_{3}}^{2} \end{matrix}$	13.88	1	13.88	30.05	< 0.0001	显著
$\begin{matrix} {X_{4}}^{2} \end{matrix}$	2.66	1	2.66	5.76	0.0298	显著
残差	6.93	15	0.46	-	-
失拟项	6.93	10	0.69	-	-
标准差	0.000	5	0.000	-	-
总模型	47.26	29	-	-	-

表6 方差分析(回弹变形量目标) Table 6 Variance analysis(rebound value)

表7 目标量确定系数分析 Table 7 Determine coefficient analysis

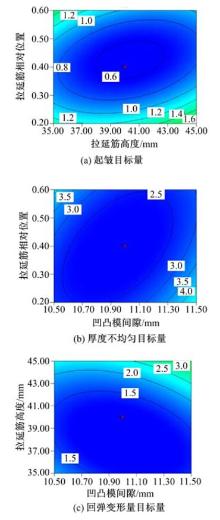
由以上各个模型方差分析(表4、表5、表6)可知, 在4个因素交互作用下, 对于起皱目标函数、厚度不均匀目标函数、回弹变形量目标函数影响最显著的交叉因素分别为:拉延筋高度× 拉延筋相对位置、凸凹模间隙× 拉延筋相对位置、凸凹模间隙× 拉延筋高度。为进一步分析各个工艺参数对3个响应优化量的影响, 现分别作各交叉因素的等高线图加以分析。图3(a)为凸凹模间隙为11 mm, 凹模入口圆角半径为45 mm时起皱目标函数与“ 拉延筋高度× 拉延筋相对位置” 的等高线图, 图3(b)为凸凹模间隙为45 mm, 拉延筋高度为40 mm时厚度不均匀目标函数与“ 凸凹模间隙× 拉延筋相对位置” 的等高线图, 图3(c)为凹模圆角半径为45 mm, 拉延筋相对位置为0.4时回弹变形量目标函数与“ 凸凹模间隙× 拉延筋高度” 的等高线图。

	Figure Option View Download New Window
	图3 3个目标量的等高线图Fig.3 Contour plot of three objective values

从图3(a)可以看出, 响应值起皱目标量随着拉延筋相对位置的增大逐渐减小, 但当拉延筋相对位置达到0.4时起皱目标量随着拉延筋相对位置的增大而增大。对于拉延筋高度而言, 起皱目标量随着拉延筋高度的增大而逐渐减小, 当拉延筋高度达到40 mm时, 随着其值的增大起皱目标量逐渐增大。此外, 由等高线图可知, 起皱目标量主要分布在0.8~1.6, 属于理想范围。由图3(b)可知, 厚度不均匀目标量随着拉延筋相对位置的增大而逐渐减小, 当拉延筋相对位置为0.5时, 随着其值的增大, 厚度不均匀目标量是逐渐增大的。同理, 对于凸凹模间隙变化量, 响应值随着凸凹模间隙的增大而减小, 但当凸凹模间隙为11.2 mm时继续增大凸凹模间隙, 厚度不均匀目标量随之增大。由图3(c)可知, 回弹变形目标量随着拉延筋高度和凸凹模间隙的增大而增大。但由整个等高线图可知, 回弹变形目标量小于3, 即封头的平均回弹变形量值小于3, 在理想范围内。

3 试验方案优化与验证

在上述结果分析与模型拟合的基础上利用Design-Expert V8.0.6软件对试验参数进一步优化^[14], 即在起皱目标量、厚度不均匀目标量、平均回弹变形目标量三者之间取得最佳效果的情况下, 确定各个工艺参数的最优取值。表8为保证起皱目标量小于2、厚度不均匀目标量小于4、回弹变形目标量小于2的基础上获得的优化方案。

表8 工艺优化方案 Table 8 Program of process optimization

为了进一步验证该优化方案的可信度, 为后续实际生产提供正确数据, 表8中5组优化方案被运用于dynaform软件中进行有限元仿真模拟, 其结果如表9所示。

表9 验证工艺参数结果分析 Table 9 Test parameters validation and result analysis

表9中预测值e₁是通过响应面优化得到的响应值, 模拟值e₂是对应的优化工艺参数进行有限元分析得到的各个响应值。误差计算公式如式(9)所示^{[13, 14]}:

$\begin{matrix} e = \frac{e_{1} - e_{2}}{e_{2}} \times 100 % (9) \end{matrix}$

如表9所示, 5组优化方案中各个响应值的误差绝对值均小于7.4%, 说明通过响应面优化得到优化工艺方案可信度高。此外, 方案3各个响应值的误差绝对值均小于5%, 说明该方案稳定性最好, 因此把方案3各参数组合作为最优工艺参数组合并用于实际生产。

图4(b)为采用优化后的工艺参数冲压成形的⌀3000× 10 mm的封头件。由图4可知, 新型冲压工艺生产的封头无起皱鼓包缺陷。使用智能超声波测厚仪对成形后封头进行厚度测量, 封头最薄处料厚为9.7 mm, 最大料厚为10.3 mm, 且厚度分布较均匀。使用回弹角测量仪对成形封头回弹角进行测量, 测得最大回弹角为3° 。综上所述, 最优工艺参数组合生产出的零件能够很好地满足工艺要求, 并有效保证了封头件的表面质量、尺寸精度和形状精度。

	Figure Option View Download New Window
	图4 优化前后的封头成形件Fig.4 Heads formed before and after optimization

4 结论

(1)针对某封头制造厂封头成形工艺出现的问题, 对原有热冲压成形工艺参数进行多目标优化, 得到该封头成形工艺参数的最优组合, 即凸凹模间隙t=10.7 mm、凹模圆角半径R=43.43 mm、拉延筋高度H=43.12 mm、拉延筋相对位置L=0.47。

(2)采用Design-Expert 8.0.6和Matlab的数据处理技术相结合对封头冲压工艺参数进行试验设计、结果分析和优化处理, 并得到了多目标优化回归模型。

(3)经误差优化分析和生产实践验证, 采用最优成形工艺参数组合能够生产出表面质量好、尺寸精度高和形状误差小的封头零件, 大大减小了成品报废率, 经济效益十分显著。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	罗征志, 曾京, 黄烈兵, 等. 铁路罐车封头冲压成形研究[J]. 西南交通大学学报, 2013, 4(4): 19-23. Luo Zheng-zhi, Zeng Jing, Huang Lie-bing, et al. The study of stamping heads in rail tanker[J]. Journal of Southwest Jiaotong University, 2013, 4(4): 19-23. [本文引用:1]
[2]	Chakrabarty J. Theory of stretch forming over hemispherical punch heads[J]. International Journal of Mechanical Sciences, 1970, 12(4): 315-325. [本文引用:1]
[3]	Chao Y J, Sutton M A. Stress concentration factors for nozzles in ellipsoidal pressure vessel heads due to thrust loads[J]. International Journal of Pressure Vessels and Piping, 1985, 19(1): 69-81. [本文引用:2]
[4]	Fiorentino A, Ceretti E, Attanasio A, et al. Analysis of forces, accuracy and formability in positive die sheet incremental forming[J]. International Journal of Material Forming, 2009, 2(1): 805-808. [本文引用:1]
[5]	Durante M, Formisano A, Langella A, et al. The influence of tool rotation on an incremental forming process[J]. Journal of Materials Processing Technology, 2009, 209(9): 4621-4626. [本文引用:1]
[6]	Zhang J H, Zhan M, Yang H, et al. 3D-FE modeling for power spinning of large ellipsoidal heads with variable thicknesses[J]. Computational Materials Science, 2011, 53(1): 303-313. [本文引用:1]
[7]	杨小强, 孙家根, 戴龙林, 等. 球形封头不锈钢衬里冲压成形与回弹过程的数值模拟与分析[J]. 中国制造业信息化, 2004, 33(5): 113-115. Yang Xiao-qiang, Sun Jia-gen, Dai Long-lin, et al. The numerical analysis of stamping forming and springback process for spherical head's stainless steel lining[J]. Manufacture Information Engineering of China, 2004, 33(5): 113-115. [本文引用:1]
[8]	刘士士, 谷正气, 伍文广, 等. 基于响应面方法的车辆多目标协同优化[J]. 中南大学学报: 自然科学版, 2012, 43(7): 2586-2592. Liu Shi-shi, Gu Zheng-qi, Wu Wen-guang, et al. Multi-objective collaborative optimization of vehicle based on response surface methodology[J]. Journal of Central South University (Science and Technology), 2012, 43(7): 2587-2592. [本文引用:1]
[9]	Schenk O, Hillmann M. Optimal design of metal forming die surfaces with evolution strategies[J]. Computers and Structures, 2004, 82(20): 1695-1705. [本文引用:1]
[10]	Palanivel R, Mathews P K. Prediction and optimization of process parameter of friction stir welded AA5083-h111 aluminum alloy using response surface methodology[J]. Journal of Central South University of Technology, 2012, 19(1): 1-8. [本文引用:1]
[11]	Nasef M M, Aly A A, Saidi H, et al. Optimization of reaction parameters of radiation induced grafting of 1-vinylimidazole onto poly (ethylene-co-tetraflouroethene) using response surface method[J]. Radiation Physics and Chemistry, 2011, 80(11): 1222-1227. [本文引用:1]
[12]	Zhao W, Qiu Z P. An efficient response surface method and its application to structural reliability and reliability-based optimization[J]. Finite Elements in Analysis and Design, 2013, 67: 34-39. [本文引用:1]
[13]	Sun G Y, Li G Y, Zheng G, et al. Multi-objective optimization for sheet metal formnig of drawing with successive response surface method[J]. Acta Mechanica Sinica, 2010, 42(2): 245-255. [本文引用:2]
[14]	刘佳, 张宏, 石岩. 基于Design-Expert V7设计的不锈钢激光非熔透搭接焊工艺优化研究[J]. 机械工程学报, 2011, 47(16): 52-60. Liu Jia, Zhang Hong, Shi Yan. Technology optimizing research on laser nonpenetration lap welding of stainless steel based on Design-ExpertV7[J]. Journal of Mechanical Engineering, 2011, 47(16): 52-60. [本文引用:2]

2013

0.0

... 针对椭圆封头冲压成形问题国内研究学者进行了一系列的研究工作,包括对封头拉延成形工艺的研究分析,对大型椭圆封头成形加工的坯料尺寸、成形载荷的计算,对封头成形冲压模具结构的设计,以及采用有限元仿真模拟软件对封头冷冲压成形的分析^[1] ...

1970

0.0

... 国外学者Chakrabarty、Chao等在对压力容器封头进行受力分析的基础上,对半球形零件的模具冲压成型进行试验研究^[2,3] ...

1985

0.0

... 国外学者Chakrabarty、Chao等在对压力容器封头进行受力分析的基础上,对半球形零件的模具冲压成型进行试验研究^[2,3] ...

... ₂,成为整个封头件胀形变形区,该处材料有变薄趋势^[3] ...

2009

0.0

... Fiorentino等^[4]对金属板料旋压时的受力、成形精度开展了试验研究,Durante^[5]分析了成形辊旋压对旋压成形的影响 ...

2009

0.0

... Fiorentino等^[4]对金属板料旋压时的受力、成形精度开展了试验研究,Durante^[5]分析了成形辊旋压对旋压成形的影响 ...

2011

0.0

... 针对椭圆封头冲压成形多数研究基本上从单因素方面单目标来分析预测成形过程^[6,7] ...

2004

0.0

... 针对椭圆封头冲压成形多数研究基本上从单因素方面单目标来分析预测成形过程^[6,7] ...

2012

0.0

... 经实践生产验证,能够得到成形表面质量好、厚度减薄均匀以及回弹变形量合理的封头件^[8] ...

2004

0.0

... 根据Hillmann等^[9]对起皱成形极限曲线的定义,构建起皱D_w、厚度不均匀D_t、平均回弹变形量D_s相应的目标函数如下: ...

2012

0.0

... 2 响应面的优化试验设计响应面法的使用必须先确定合理的因素以及相应的水平参数^[10] ...

2011

0.0

... 为了得到合理的回归方程,选择最陡坡试验和中心复合设计(Center composite design,CCD)相结合来设计试验,每个因子所取的水平数为5个^[11] ...

2013

0.0

... 01时,即认为该指标是高度显著^[12] ...

2010

0.0

... 此外,还可通过R²和R_adj进一步检验模型的可靠性,一般情况下认为R²和R_adj值越大,则回归模型的拟合精度越高^[13] ...

... 误差计算公式如式(9)所示^[13,14]: ...

2011

0.0

... 6软件对试验参数进一步优化^[14],即在起皱目标量、厚度不均匀目标量、平均回弹变形目标量三者之间取得最佳效果的情况下,确定各个工艺参数的最优取值 ...

... 误差计算公式如式(9)所示^[13,14]: ...