作者简介:巴特(1987-),男,博士研究生.研究方向:混合动力汽车关键技术.E-mail:b1987628@126.com
为了解决混合动力汽车工作过程中的模式频繁切换问题,提出一种集成多方法的混合动力汽车模式频繁切换问题解决方案。该方案综合采用了基于计时、滤波、模糊逻辑和滞回的方法抑制模式的频繁切换。经仿真验证,采用该方案后,模式持续时间小于4 s情况所占比例由85%降为3%,模式切换次数减少了80%,同时,车辆的车速跟随、SOC平衡情况和动力性没有受到显著影响,当量冲击度的最大值和平均值分别减少了42%和61.4%,整车经济性提高了9.4%。
In order to solve the issue of frequent mode-switch of hybrid electric vehicle, a new scheme is proposed. The scheme integrates the time based, filter based and fuzzy logical and hysteresis based methods. Simulation results show that adopting the proposed scheme the percentage of mode duration less than 4 s is reduced from 85% to 3%, which mean that the number of mode switching falls nearly 80%. Meanwhile, the actual vehicle velocity follows the desired velocity and the charge maintains within a narrow operating band as well. The maximum and average impact equivalent degrees are reduced by 42% and 61.4%, and the fuel economy of the vehicle is improved by 9.4%.
近年来, 混合动力汽车(HEV)成为了汽车领域的研究热点[1, 2]。混合动力汽车行驶过程中, 其能量分配策略会根据具体行驶工况将混合动力汽车控制在不同的工作模式, 然后在各个工作模式下分别控制各个动力源的工作状态。现有的关于混合动力汽车控制策略的研究在混合动力汽车工作模式划分、各模式切换条件的制定[3, 4, 5, 6, 7]、模式切换的协调控制[8, 9, 10, 11]等方面奠定了坚实的基础。根据现有的能量分配策略, 一般而言, 加速踏板信号、制动踏板信号、车速、电池SOC等信号都会直接或间接决定车辆当前工作在何种工作模式。这些信号在特定工况下频繁波动时, 会造成车辆工作模式的频繁切换, 从而对车辆的平顺性、经济性以及相关部件的寿命造成不良的影响。因此, 本文针对混合动力汽车的模式频繁切换问题提出了集成基于计时、滤波、模糊逻辑和滞回的解决方案。最后, 仿真分析了该方案的有效性和合理性。
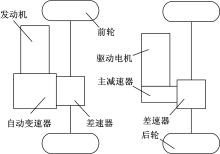
本文采用一种简单的四驱形式的混合动力构型, 在传统汽车的基本结构不变的基础上在后轴加一个驱动电机, 如图1所示。
根据构型特点, 该混合动力汽车的工作模式可以分6种:纯电动模式(MD); 发动机单独驱动模式(ED); 发动机驱动且驱动电机充电模式(ECD); 发动机和驱动电机联合驱动模式(BD); 制动能量回收模式(RB); 停车模式(STOP)。
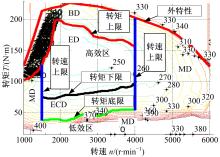
该混合动力汽车的控制策略采用目前在实车控制器中常用的逻辑门限值策略, 控制策略根据制动踏板开度、需求转矩、发动机转速、车速、电池SOC等信号进行模式之间的划分, 其核心思想是控制发动机工作在一个经济性较好的区域, 各驱动模式在发动机map图上对应的区域如图2所示。
由图2可知, 当需求转矩在转矩上限、转矩下限或者转矩底限附近波动, 或者当前车速经传动比换算成的等效发动机转速在转速下限或者转速上限附近波动时, 车辆的工作模式会在BD、ED、ECD、MD之间频繁切换; 另外, 当制动踏板信号和加速踏板信号交替波动时, 车辆的工作模式也可能在驱动和制动能量回收模式之间频繁切换。
为了解决混合动力汽车特定工况下模式频繁切换的问题, 在不对车辆性能造成显著影响的前提下有效地减少不必要的模式切换, 本文提出基于时长、滤波和带模糊逻辑的滞回3种解决方案。
频繁的模式切换的具体表现之一就是车辆的工作模式中出现了持续时间很短的模式。针对这种情况, 从模式持续的时长方面采用下述两种解决方案:
(1)采用计时模块滤除持续时间较短的模式
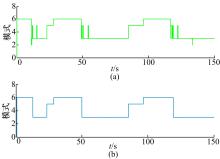
根据模型调试和实车运行的数据确定一个合适的时间阈值来进行短时行驶模式的滤除。当依据能量分配算法得到的行驶模式持续的时间小于给定的阈值时, 忽略当前能量分配策略给出的行驶模式, 而维持上一时刻的行驶模式; 当依据能量分配策略计算得到的行驶模式持续的时间大于给定的阈值时, 切换到当前能量分配策略得到的行车模式。如图3所示, 图3(a)为根据能量分配策略得到的工作模式, 图3(b)为滤除持续短时的工作模式后的车辆行车模式。
(2)对车辆行驶模式的最短时间进行限制
上述方法能够有效滤除持续时间小于给定阈值的行驶模式, 但是当行驶模式持续的时长稍微大于给定的时间阈值时, 仍然会出现持续时间很短的行驶模式。这会使得车辆还没有达到当前模式下的稳态工作状态就切换到了下一个模式, 影响车辆的控制品质。因此这里对车辆在各个模式下行驶的最短时长进行限制:一旦车辆进入某一个行车模式时即开始计时, 当计时时间小于给定值时, 不允许车辆退出该模式; 只有当在该模式下持续的时间超过给定的最短时长后才允许车辆根据当前的能量分配需求切换到其他模式。如图4所示, 图4(a)为滤除短时工作模式后得到的工作模式, 图4(b)为对各个模式最短行驶时间进行限制后得到的车辆行车模式。
频繁的模式切换还可能表现在车辆的工作模式随着加速踏板信号、制动踏板信号等与模式切换直接相关的信号的频繁波动而波动。为保证车辆良好的动力响应特性, 不能直接将这些信号的波动去除, 但是却可以将用于模式切换的这些关键信号进行滤波处理, 去除不必要的信号尖峰, 达到抑制模式频繁切换的目的。
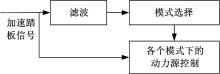
以加速踏板信号为例, 如图5所示, 将加速踏板进行滤波, 然后将滤波后的加速踏板信号用于混合动力汽车工作模式的选择。同时, 各个模式下的动力源控制仍采用未经滤波的加速踏板信号。
本文采用一阶延时滤波对加速踏板信号进行滤波处理, 其表达式为:
式中:y(k)为本次滤波输出值; y(k-1)为上次滤波输出值; x(k)为本次采样值; Q为滤波系数, 满足Q=T/(T+τ ), 其中T为采样周期, τ 为数字滤波器的时间常数。
取一段时长的加速踏板信号如图6(a)所示, 对其进行一阶延时滤波后该加速踏板信号如图6(b)所示。
由图6可知, 经过一阶延时滤波后, 滤除了加速踏板信号的部分尖峰, 使得加速踏板信号变得平滑。因此, 采用滤波后的信号进行模式选择可有效避免信号尖峰导致的短时、频繁的模式切换。滤波后再进行模式选择会使得模式的切换存在一定的滞后, 但是, 由于这里各个模式下动力源控制仍然采用不滤波的加速踏板信号, 因此, 不会对车辆的动力响应产生显著影响, 只会使得动力源的工作点分布发生变化。
当车速、SOC等缓变信号在模式切换门限值附近小范围波动时, 也会造成模式的频繁切换, 这时采用滞回的方法可以有效地避免这种情况。
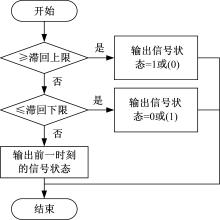
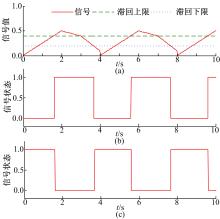
滞回与逻辑运算中的“ ≥ ” 和“ ≤ ” 相对应。如图7所示, 逻辑运算中“ ≥ ” 对应的滞回的基本逻辑为:当信号大于上限时状态变为1, 直到小于下限时才变为0; 逻辑运算中“ ≤ ” 对应的滞回的基本逻辑为:当信号大于上限时状态变为0, 直到小于下限时才变为1; 信号值经过“ ≥ ” 和“ ≤ ” 对应的滞回判断后的信号状态分别如图8(a)和图8(b)所示。
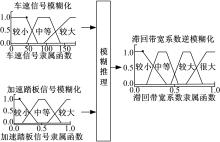
滞回上下限之间的距离决定了滞回的效果。一般情况下难以根据现有的数据得到确定的滞回上下限之间的距离, 只能知道影响该滞回带宽的变量和该变量对带宽的影响。例如, 车速的滞回与车速的大小以及加速踏板信号的大小相关。车速大、加速踏板开度大时, 为了避免车速信号的波动导致工作模式的频繁切换, 滞回带宽应该较大。因此, 这里采用模糊逻辑的方法来求取滞回带的宽度。首先, 对车速信号和加速踏板信号进行模糊化, 然后依据表1中的模糊规则进行模糊推理, 最终将得到的滞回带宽系数进行逆模糊化, 如图9所示。
| 表1 模糊规则表 Table 1 Linguistic rules table |
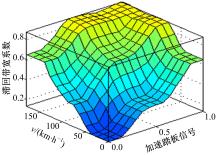
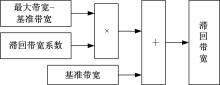
求解滞回带宽时, 首先, 根据信号的特点制定一个基准的带宽和最大带宽, 然后将求得的滞回带宽系数乘以最大带宽与基准带宽的差值, 最后再加上基准带宽即得到滞回带宽, 如图11所示。
采用结合模糊逻辑的滞回时, 滞回上限(或下限)采用门限值或者其他的信号值(如发动机转矩上限、下限、底限等), 而相应的下限(或上限)即为下限值(或上限)加去(或减去)滞回带宽。
采用上述的基于滤波的方法对加速踏板信号进行滤波处理; 采用上述的基于模糊逻辑和滞回的方法对车速、转矩上限、转矩下限等门限值信号进行处理; 最后, 采用计时模块滤除持续时间较短的模式后对车辆行驶模式的最短时间进行限制。
在Simulink中搭建能量分配控制策略模型和上述的模式切换频繁抑制模型, 在AVL Cruise中搭建整车模型。然后, 通过联合仿真, 分别从模式频繁程度、车速跟随和SOC平衡情况、动力性、经济性和平顺性几个方面综合对比应用本文提出的模式切换频繁问题解决方案前后车辆各个方面的表现。
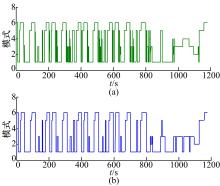
分别从模式持续时长分布和模式切换次数两方面定量分析模式切换频繁程度。仅采用简单逻辑门限值的控制策略在NEDC工况下的模式如图12(a)所示, 而采用了本文提出的解决方案后, 对应的模式如图12(b)所示。
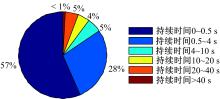
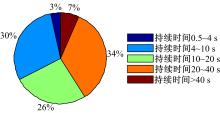
由图12可知, 与原控制策略相比, 采用本文提出的解决方案后, 大量短时的、频繁的模式被滤除掉了。经统计, 处理前, 车辆的工作模式发生了424次变化, 而处理后车辆的工作模式仅发生了82次变化, 模式切换的次数有了大幅度的减小。对处理前后模式持续的时间进行统计, 结果如图13和图14所示。处理前, 车辆有57%的模式持续的时间小于0.5 s, 85%的模式持续的时间小于4 s; 而处理后, 车辆没有持续时间低于0.5 s的模式, 仅有3%的模式持续的时间小于4 s。因此, 模式切换频繁问题得到了有效的解决。
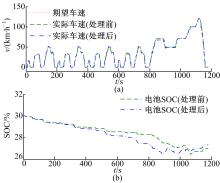
如图15(a)所示, 处理前后实际车速都很好地跟随着期望车速。如图15(b)所示, 处理前后电池电量的变化相差也基本相同。本文控制方案在解决模式切换频繁问题的同时, 并没有对车速的跟随和电池SOC的平衡造成显著影响。
由于在全负荷加速以及爬坡工况中并不存在频繁的模式切换和短时工作模式, 因此, 处理前后车辆的各项动力性指标不变, 如表2所示。
| 表2 车辆动力性表现 Table 2 Power performance of HEV |
由于处理后滤除了短时的工作模式, 减少了发动机、电机等动力源在模式切换时非稳态工作状态下的工作时间, 车辆的经济性较处理前有了提高。处理前仿真得到NEDC工况下的综合油耗为6.4 L/100 km, 处理后仿真得到NEDC工况下的综合油耗为5.8 L/100 km, 经济性提高了9.4%。
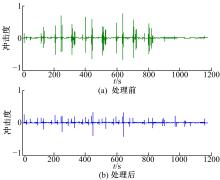
由于本文并没有研究模式切换时的动态协调问题, 这里仅考虑模式处理前后冲击度的相对大小, 采用归一化的方法比较处理前后的当量冲击度, 如图16所示。
对图16中的当量冲击度进行统计, 如表3所示。对比可知, 修改前后, 当量冲击度的最大值减小了42.0%, 平均值减小了61.4%, 因此, 处理后车辆的平顺性得到了提高。
| 表3 处理前后的当量冲击度比较 Table 3 Comparison of equivalent jerk before and after processing |
提出了基于时长、滤波、模糊逻辑和滞回的模式切换频繁解决方案。经仿真验证, 本文方案运用于抑制混合动力模式频繁切换问题时, 滤除了模式持续时间小于0.5 s的情况, 持续时间小于4 s所占比例也由85%降为3%, 而且模式切换的次数也由424次降低到82次, 有效地达到了减小模式切换频率的目的; 同时, 该方案对车辆的车速跟随、SOC平衡情况和动力性没有显著影响; 另外, 采用该方案后, 车辆的经济性提高了9.4%; 在平顺性方面, 车辆的当量冲击度最大值和平均值分别减少了42%和61.4%。因此, 该方案能合理并有效地解决混合动力汽车的模式切换频繁问题。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|