基于整数数据的文档压缩编码方案

引用本文

特日跟, 江晟, 李雄飞, 李军. 基于整数数据的文档压缩编码方案. 吉林大学学报: 工学版, 2016, 46(1): 228-234
TE Ri-gen, JIANG Sheng, LI Xiong-fei, LI Jun. Document compression scheme based on integer data. Journal of Jilin University Engineering and Technology Edition, 2016, 46(1): 228-234 复制到剪切板

Permissions

基于整数数据的文档压缩编码方案

特日跟^1,^2,^3,⁴, 江晟^1,², 李雄飞^3,⁴, 李军^3,⁴

1.长光卫星技术有限公司,长春 130000

2.中国科学院长春光学精密机械与物理研究所,长春 130033

3.吉林大学符号计算与知识工程教育部重点实验室,长春 130012

4.吉林大学计算机科学与技术学院,长春 130012

李雄飞(1963-),男,教授.博士生导师.研究方向:数据库,数据挖掘.E-mail:xiongfei@jlu.edu.cn

作者简介:特日根(1987-),男,博士研究生.研究方向:数据挖掘.E-mail:277093537@qq.com

基金:吉林省自然科学基金项目(201115020)

摘要

提出了针对整数数据的CSN-2压缩算法,并将其应用于任意文档的压缩,且CSN-2压缩算法不需额外的数据支持。通过研究CSN-2解压算法,提出了可以正确还原原数据的CSNE-2解压算法,并对解压算法结果的唯一性和正确性进行了理论及实验检验。并通过与其他压缩方案的实验比较,结果表明CSN-2压缩算法对整数型文档具有较高的压缩率,且对任意文档均具有压缩效果。

关键词: 计算机软件; 数据压缩; 压缩编码; 文本压缩; 整数数据

中图分类号:TP301 文献标志码:A 文章编号:1671-5497(2016)01-0228-07

Document compression scheme based on integer data

TE Ri-gen^1,^2,^3,⁴, JIANG Sheng^1,², LI Xiong-fei^3,⁴, LI Jun^3,⁴

1.Chang Guang Satellite Technology Co.,Ltd.,Changchun 130000,China

2.Changchun Institute of Optics,Fine Mechanics and Physics,Chinese academy of Science,Changchun 130033,China

3.Key Laboratory of Symbol Computation and Knowledge Engineering of Ministry of Education,Jilin University, Changchun 130012,China

4.College of Computer Science and Technology, Jilin University, Changchun 130012, China

Abstract

A CSN-2 compression algorithm for integer data was proposed and applied to the compression of any documents. Moreover, the CSN-2 data compression algorithm does not need additional data support. A CSNE-2 decompression algorithm, which can properly restore the original data, was proposed by studying the CNS-2 decompression algorithm. It was proved that the results of the decompression algorithm are unique and correct in theoretical and experimental tests. Furthermore, it was demonstrated that the CSN-2 compression algorithm for the integer type of documents has a higher compression ratio, and could compress any documents compared with experiments of other compression programs.

Keyword: computer software; data compression; compression; text compression; integer data

Show Figures

0 引言

随着多媒体计算机技术、计算机网络技术以及现代多媒体通信技术的不断发展, 数据业务和多媒体通信业务等通信量越来越大, 给信息存储特别是网络传输带来前所未有的压力。现有数据压缩算法分为有损压缩和无损压缩^[1]。有损压缩通过数据挖掘等手段从数据来源、数据特性出发, 提取关键信息予以保存。语音识别、医学和生物测量^[2]、股票价格、市场销售数据、气象数据、电信通信、传感器网络数据等均可采用有损压缩方法处理。有损压缩方法可分为基于概率模型^[3]、基于时间序列分析模型^[4]、基于数据挖掘模型^[5]、基于数据压缩模型^[6]这四类, 其共性在于压缩率高, 数据还原质量依赖于算法实现的代价。

无损压缩技术^[7]在数据压缩过程中不允许损失精度, 可以保真还原。主要用于文本文件、数据库、程序数据和特殊应用场合的图像数据(如指纹图像、医学图像)等压缩。相对于有损压缩, 无损压缩的压缩率较低, 一般为1/2~1/5。无损压缩可以分为基于统计的压缩算法和基于字典的压缩算法两类。两类压缩算法都需要一个额外数据库。本文提出的Compress sequence number(CSN)压缩算法通过增加每个字节的信息表达能力实现压缩, 本文还对解压算法结果的唯一性和正确性进行了理论及实验检验。

1 相关工作

基于统计的压缩算法的本质是根据字符的出现频率来对字符本身重新编码, 属于熵编码类, 主要算法有香浓-凡诺编码、游程长度编码、哈夫曼编码和算术编码。香浓-凡诺算法^[8]由贝尔实验室开发, 核心是构造一个通过叶子节点记录字符信息的二叉树, 它是一种自顶向下的、非自适应的编码算法。游程长度编码(Run-Length-Coding)^[9]通过去除文本中的冗余字符或字节中的冗余位, 达到减少数据文件所占的存储空间的目的, 其压缩效能取决于整个数据流的重复字符出现次数、平均游程长度及所采用的编码结构。由于该算法是针对文件的某些特点所设计的, 具有一定的局限性。Huffman编码是Huffman在1952年提出的一种基于信号概率的数据压缩算法^[10]。它根据字符重复出现的概率生成的一种前缀编码方法, 其核心也是构造二叉树, 与香浓-凡诺编码相反, 是一种自下向上的、非自适应的编码算法。1978年提出的动态哈夫曼算法^{[10, 11]}取消了统计过程, 一边压缩一边动态调整哈夫曼树, 提高了压缩效率。算术编码^[12]也是一种根据字符出现概率重新编码的压缩方案, 该方法打破了哈夫曼算法必须用整数来表示字符的限制。压缩效果逼近信息熵极限的编码方法。

字典编码方法是以较长的字符串或经常出现的字母组合构成字典中的各个词条, 并用相对较短的数字或符号来表示的方法。压缩效果与重复数据量、字典大小等因素有关。主要算法包括:LZ77算法^[13]、LZ78算法^[14]、LZSS算法^[15]、LZW算法^[16]等。LZ77算法^[13]是第一个具有实用价值的基于词典编码的数据压缩算法, 它利用一个窗口在原始数据中滑动, 超前查看缓冲区中的刚刚由输入文件中读入的未编码字符, 实现数据压缩、解压缩, 也称为基于滑动窗口的自适应的字典压缩方法。LZ78.压缩算法是LZ77的改进算法, 放弃了窗口, 采用树形结构字典保存短语, 对区间重复性强的数据压缩效果较好, 但它的编译码方法较复杂, 实现起来比较困难。LZSS算法采用二分搜索树, 解码时无须生成和维护字典树, 大大加快了速度。该算法的压缩率较高, 编译算法较简单。LZW算法^[16]是1984年Welch提出的基于LZ78算法的一个变种压缩算法。主要用于GIF格式的图像数据的压缩。该算法的压缩效果好、速度快且算法描述易于接受, 是目前最常用和最有效的无损压缩算法。

上述算法的共同特征是需要一个辅助数据库。Gö del^[17]提出一种不依赖于数据库的无损压缩方法称为哥德尔数, 但其使用范围局限于对图灵机程序的压缩, 而不具有普遍性。哥德尔数是将一组正整数序列b₁, b₂, b₃, …, b_n通过公式(1)计算得出, 其中P为递增的质数。

$\begin{matrix} 哥德尔数 = (2^{b_{1}} \times 3^{b_{2}} \times 5^{b_{3}} \times \dots \times P^{b_{n}}) (1) \end{matrix}$

由公式可知哥德尔数会随着序列长度的增加成指数增长, 因此不适合于其他类型数据的压缩。

2 CSN压缩算法

2.1 CSN-1数定义

定义1:对于长度为n, 存在最小元素为1的整数序列:b₁, b₂, b₃, …, b_n, 取T=max(b₁, b₂, b₃, …, b_n)+1, 由递推公式(2)可得CSN数。

$\begin{matrix} \{\begin{matrix} a_{0} = 0, \\ a_{k} = T \cdot a_{k - 1} + b_{k}, 1 \leq k \leq n \\ CSN = a_{n} \end{matrix} (2) \end{matrix}$

例:序列20, 53, 3, 58, 8, 17, 43, 1通过公式(2)计算可得

T=58+1=59

a₁=59× 0+20=20

a₂=59× 20+53=1233

a₃=59× 1233+3=72750

a₄=59× 72750+58=4292308

a₅=59× 4292308+8=253246180

a₆=59× 253246180+17=14941524637

a₇=59× 14941524637+43=881549953626

a₈=59× 881549953626+1=52011447263935

得该序列的CSN-1数为52011447263935。CSN-1具有明显的局限性, 要求序列中最小数只能为1, 且必须含有1, 因此需要对CSN-1进行改进。

2.2 CSN-2数定义

在CSN-1中, 若整数序列中, ∃b_i∈ $\begin{matrix} \{b_{1}, b_{2}, b_{3}, \dots, b_{n}\} \end{matrix}$ , 且b_i≤ 0或b_i≥ T, 则CSN-1在解压还原时会失效。因此提出CSN-1数的改进编码CSN-2数。

定义2:对于长度为n的整数序列:b₁, b₂, b₃, …, b_n, 取

$\begin{matrix} \begin{matrix} M = \min (b_{1}, b_{2}, b_{3}, \dots, b_{n}), \\ T = \max (b_{1}, b_{2}, b_{3}, \dots, b_{n}) - M + 2 \end{matrix} \end{matrix}$

由递推公式(2)可得CSN数。

$\begin{matrix} \{\begin{matrix} a_{0} = 0 \\ \begin{matrix} a_{k} = T \cdot a_{k - 1} + (b_{k} - (M - 1)) & 1 \leq k \leq n \end{matrix} \\ CSN = a_{n} \end{matrix} (3) \end{matrix}$

例:序列20, 53, 3, 58, 8, 17, 43, 10通过公式(3)计算可得:

M=3

T=58-3+2=57

a₁=57× 0+20-2=18

a₂=57× 17+53-2=1077

a₃=57× 1077+3-2=61390

a₄=57× 61390+58-2=3499286

a₅=57× 3499286+8-2=199459308

a₆=57× 199459308+17-2=11369180571

a₇=57× 11369180571+43-2=648043292588

a₈=57× 648043292588+10-2=36938467677524

得:该序列的CSN-2数为36938467677524

因为CSN-1的局限性, 文章随后的实验均使用CSN-2来完成。

2.3 CSN-2压缩原理

CSN的压缩原理就是针对CSN数进行二进制存储。因为原序列通常是以字符串形式或占用完整机器位数来存储和传输, 且具有一定的局部聚合性, 因此CSN数是通过整数数据中局部数据范围比全文小的特点, 将数据分段, 利用其剩余的机器位数, 减少无用空间, 进而实现压缩。

例:序列20, 53, 3, 58, 8, 17, 43, 10。

序列的CSN数为34948661300524。

CSN数对应的二进制数为111111|11001001|00011110|10001010|11001101|00101100。

该序列在不同情况下所占空间如表1所示。

表1 CSN压缩数与原数据的比较 Table 1 CSN compressed with the original data

2.4 CSNE解压原理

CSNE解压算法是CSN压缩算法的逆过程, 将每个压缩段按压缩的逆过程进行还原, 公式(4)和公式(5)分别为CSN-1和CSN-2压缩算法的逆运算, 即为CSNE-1和CSNE-2解压算法。

由公式(2)得(rem为取余运算)CSN-1的解压公式(4), 其中当a_k=0时, 递归结束。

由公式(3)得(rem为取余运算)CSN-2的解压公式(5), 其中当a_k=0时, 递归结束。

例:一个序列的CSN-2数为36938467677524, T=57, M=3

因此最终还原出序列为:20, 53, 3, 58, 8, 17, 43, 10

2.5 CSN正确性

定理1:每个整数序列可对应一个且唯一的一个CSN-1数。

定理2:每个整数序列可对应一个且唯一的一个CSN-2数。

CSN-2编码过程是将序列先整体平移, 使得序列中最小元素为1, 在满足CSN-1条件的基础上, 通过使用CSN-1的压缩方法进而完成其压缩过程。CSNE-2的解压过程, 则是将CSN-2数先通过CSNE-1的解压过程得到序列, 通过平移还原为原序列, 因此若定理1成立, 则定理2也成立。

定理1证明:

设两个序列C¹和C², 其中C¹为 $\begin{matrix} C_{1}^{1} \end{matrix}$ , $\begin{matrix} C_{2}^{1} \end{matrix}$ , $\begin{matrix} C_{3}^{1} \end{matrix}$ , …, $\begin{matrix} C_{n}^{1} \end{matrix}$ ; C²为 $\begin{matrix} C_{1}^{2} \end{matrix}$ , $\begin{matrix} C_{2}^{2} \end{matrix}$ , $\begin{matrix} C_{3}^{2} \end{matrix}$ , …, $\begin{matrix} C_{m}^{2} \end{matrix}$ , 对C¹和C²使用相同的T进行压缩时, 可得到同一个CSN。

当n≠ m时, 假设n> m, 通过公式(2)可得

CSN=T^n-¹ $\begin{matrix} C_{1}^{1} \end{matrix}$ +T^n-² $\begin{matrix} C_{2}^{1} \end{matrix}$ +…+T $\begin{matrix} C_{n - 1}^{1} \end{matrix}$ + $\begin{matrix} C_{n}^{1} \end{matrix}$ =

T^m-¹ $\begin{matrix} C_{1}^{2} \end{matrix}$ +T^m-² $\begin{matrix} C_{2}^{2} \end{matrix}$ +…+T $\begin{matrix} C_{m - 1}^{2} \end{matrix}$ + $\begin{matrix} C_{m}^{2} \end{matrix}$ ,

所以:

$\begin{matrix} \begin{matrix} T^{n - 1} C_{1}^{1} + \dots + T^{m} C_{n - m}^{1} + T (T^{m - 2} C_{n - m + 1}^{1} + \\ \dots + C_{n - 1}^{1} - T^{m - 2} C_{1}^{2} - \dots - C_{m - 1}^{2}) = C_{m}^{2} - C_{n}^{1} \end{matrix} \end{matrix}$

又因为:

$\begin{matrix} \begin{matrix} T^{n - 1} C_{1}^{1} + \dots + T^{m} C_{n - m}^{1} + T (T^{m - 2} C_{n - m + 1}^{1} + \\ \dots + C_{n - 1}^{1} - T^{m - 2} C_{1}^{2} - \dots - C_{m - 1}^{2}) T^{n - 1} C_{1}^{1} + \\ \dots + T^{m} C_{n - m}^{1} + T (T^{m - 2} C_{n - m + 1}^{1} + \\ \dots + C_{n - 1}^{1} - T^{m - 2} C_{1}^{2} - \dots - C_{m - 1}^{2}) > \\ T^{n - 1} C_{1}^{1} + \dots + T^{m} C_{n - m}^{1} + T (T^{m - 2} (1 - T) + \\ T^{m - 3} (1 - T) + (1 - T)) = \\ T^{n - 1} C_{1}^{1} + \dots + T^{m} C_{n - m}^{1} + T (1 - T^{m - 2}) = \\ T^{n - 1} C_{1}^{1} + \dots + T^{m} C_{n - m}^{1} + T - T^{m - 1} > \\ T^{n - 1} C_{1}^{1} + \dots + T^{m} C_{n - m}^{1} + T > T \end{matrix} \end{matrix}$

及 $\begin{matrix} C_{m}^{2} \end{matrix}$ - $\begin{matrix} C_{n}^{1} \end{matrix}$ < T,

所以

T^n-¹ $\begin{matrix} C_{1}^{1} \end{matrix}$ +…+T^m $\begin{matrix} C_{n - m}^{1} \end{matrix}$ +T(T^m-² $\begin{matrix} C_{n - m + 1}^{1} \end{matrix}$ +

…+ $\begin{matrix} C_{n - 1}^{1} \end{matrix}$ -T^m-² $\begin{matrix} C_{1}^{2} \end{matrix}$ -…- $\begin{matrix} C_{m - 1}^{2} \end{matrix}$ )> $\begin{matrix} C_{m}^{2} \end{matrix}$ - $\begin{matrix} C_{n}^{1} \end{matrix}$ ,

即等式不成立。所以n> m时, 等式不成立。

同理可得n< m时, 等式也不成立。所以当n≠ m时, 等式不成立, 即n=m。

当n=m时, 通过公式(2)可得:

$\begin{matrix} \begin{matrix} CSN = T^{n - 1} C_{1}^{1} + T^{n - 2} C_{2}^{1} + \dots + T C_{n - 1}^{1} + C_{n}^{1} = \\ T^{m - 1} C_{1}^{2} + T^{m - 2} C_{2}^{2} + \dots + T C_{m - 1}^{2} + C_{m}^{2} \end{matrix} \end{matrix}$

所以:

T(T^n-² $\begin{matrix} C_{1}^{1} \end{matrix}$ +T^n-³ $\begin{matrix} C_{2}^{1} \end{matrix}$ +…+ $\begin{matrix} C_{n - 1}^{1} \end{matrix}$ -T^n-² $\begin{matrix} C_{1}^{2} \end{matrix}$ -

T^n-³ $\begin{matrix} C_{2}^{2} \end{matrix}$ -…- $\begin{matrix} C_{n - 1}^{2} \end{matrix}$ )= $\begin{matrix} C_{n}^{2} \end{matrix}$ - $\begin{matrix} C_{n}^{1} \end{matrix}$ ,

若 $\begin{matrix} C_{n}^{2} \end{matrix}$ ≠ $\begin{matrix} C_{n}^{1} \end{matrix}$ , 又 $\begin{matrix} |C_{n}^{2} - C_{n}^{1}| \end{matrix}$ < T, 且 $\begin{matrix} C_{n}^{2} \end{matrix}$ - $\begin{matrix} C_{n}^{1} \end{matrix}$ ≠ 0,

所以:

$\begin{matrix} |\begin{matrix} T^{n - 2} C_{1}^{1} + T^{n - 3} C_{2}^{1} + \dots + C_{n - 1}^{1} \\ - T^{n - 2} C_{1}^{2} - T^{n - 3} C_{2}^{2} - \dots - C_{n - 1}^{2} \end{matrix}| \end{matrix}$ =

$\begin{matrix} |\begin{matrix} T^{n - 2} (C_{1}^{1} - C_{1}^{2}) + T^{n - 3} (C_{2}^{1} - C_{2}^{2}) \\ + \dots + (C_{n - 1}^{1} - C_{n - 1}^{2}) \end{matrix}| \end{matrix}$ ≥

$\begin{matrix} |\begin{matrix} |T^{n - 2} (C_{1}^{1} - C_{1}^{2})| - |T^{n - 3} (C_{2}^{1} - C_{2}^{2})| \\ - \dots - |(C_{n - 1}^{1} - C_{n - 1}^{2})| \end{matrix}| \end{matrix}$ >

$\begin{matrix} |\begin{matrix} |T^{n - 2} (C_{1}^{1} - C_{1}^{2})| - |T^{n - 3} (C_{2}^{1} - C_{2}^{2})| \\ - \dots - |T (C_{n - 2}^{1} - C_{n - 2}^{2})| - T \end{matrix}| \end{matrix}$ =

$\begin{matrix} |\begin{matrix} |T^{n - 2} (C_{1}^{1} - C_{1}^{2})| - |T^{n - 3} (C_{2}^{1} - C_{2}^{2})| \\ - \dots - T (|(C_{n - 2}^{1} - C_{n - 2}^{2})| + 1) \end{matrix}| \end{matrix}$ ≥

$\begin{matrix} |\begin{matrix} |T^{n - 2} (C_{1}^{1} - C_{1}^{2})| - |T^{n - 3} (C_{2}^{1} - C_{2}^{2})| \\ - \dots - |T^{2} (C_{n - 3}^{1} - C_{n - 3}^{2})| - T^{2} \end{matrix}| \end{matrix}$

︙

≥ 1得:

$\begin{matrix} |\begin{matrix} T^{n - 2} C_{1}^{1} + T^{n - 3} C_{2}^{1} + \dots + C_{n - 1}^{1} \\ - T^{n - 2} C_{1}^{2} - T^{n - 3} C_{2}^{2} - \dots - C_{n - 1}^{2} \end{matrix}| \end{matrix}$ > 1, 即

$\begin{matrix} |\begin{matrix} T (T^{n - 2} C_{1}^{1} + T^{n - 3} C_{2}^{1} + \dots + C_{n - 1}^{1} \\ - T^{n - 2} C_{1}^{2} - T^{n - 3} C_{2}^{2} - \dots - C_{n - 1}^{2}) \end{matrix}| \end{matrix}$ > T。

所以当n=m且 $\begin{matrix} C_{n}^{2} \end{matrix}$ ≠ $\begin{matrix} C_{n}^{1} \end{matrix}$ 时, 等式不成立。又因为 $\begin{matrix} C_{n}^{2} \end{matrix}$ = $\begin{matrix} C_{n}^{1} \end{matrix}$ , 则 $\begin{matrix} C_{n}^{2} \end{matrix}$ - $\begin{matrix} C_{n}^{1} \end{matrix}$ =0, 所以:T^n-² $\begin{matrix} C_{1}^{1} \end{matrix}$ +T^n-³ $\begin{matrix} C_{2}^{1} \end{matrix}$ +…+ $\begin{matrix} C_{n - 1}^{1} \end{matrix}$ -T^n-² $\begin{matrix} C_{1}^{2} \end{matrix}$ -T^n-³ $\begin{matrix} C_{2}^{2} \end{matrix}$ -…- $\begin{matrix} C_{n - 1}^{2} \end{matrix}$ =0, 即T(T^n-³ $\begin{matrix} C_{1}^{1} \end{matrix}$ +T^n-² $\begin{matrix} C_{2}^{1} \end{matrix}$ +…+ $\begin{matrix} C_{n - 2}^{1} \end{matrix}$ -T^n-² $\begin{matrix} C_{1}^{2} \end{matrix}$ -T^n-³ $\begin{matrix} C_{2}^{2} \end{matrix}$ -…- $\begin{matrix} C_{n - 2}^{2} \end{matrix}$ )= $\begin{matrix} C_{n - 1}^{2} \end{matrix}$ - $\begin{matrix} C_{n - 1}^{1} \end{matrix}$ 。

同上可知, 若 $\begin{matrix} C_{n - 1}^{2} \end{matrix}$ ≠ $\begin{matrix} C_{n - 1}^{1} \end{matrix}$ , 等式不成立。所以 $\begin{matrix} C_{n - 1}^{2} \end{matrix}$ = $\begin{matrix} C_{n - 1}^{1} \end{matrix}$ 。

以此类推最终可得 $\begin{matrix} C_{1}^{2} \end{matrix}$ = $\begin{matrix} C_{1}^{1} \end{matrix}$ , $\begin{matrix} C_{2}^{2} \end{matrix}$ = $\begin{matrix} C_{2}^{1} \end{matrix}$ , …, $\begin{matrix} C_{n}^{2} \end{matrix}$ = $\begin{matrix} C_{n}^{1} \end{matrix}$ , 即C¹和C²相同。即若存在两个序列压缩后得到同一个CSN, 则这两个序列必相同。

证毕。

通过上述证明可知, 定理2亦正确。

3 实验数据分析

3.1 影响CSN-2编码压缩效率的因素

在CSNE-2解压算法中除输入CSN-2数以外, 还应包括CSN-2数的T和增值M, 因此, 在存储CSN-2文档时, 需要在文档前面加上T和M, CSN-2文档中实际存储的内容有三个, 即T、M和CSN-2数。

定义3:

$\begin{matrix} \begin{matrix} 压缩率 = \\ \frac{原文档所占空间 - 压缩后文档所占空间}{原文档所占空间} \\ \times 100 % \end{matrix} \end{matrix}$

实验1:已知序列1:1~200, T=201; 序列2:1~400, T=401; 序列3:1~800, T=801。这三个序列均以整型形式存储, 计算三个序列的CSN-2的文档大小及其压缩率。结果如表2所示。

表2 实验1三个序列的压缩率 Table 2 Experiment 1 compression ratio of three sequences

结论1:压缩率受T影响, 当M不变时, T越大压缩率越小。

实验2:已知序列1:1~200, T=201;

序列2:200~1, T=201。

序列3:共有200个整数数据, 且至少包含一个1和一个200, 其余198个整数在1~200内随机选取。T=201以上三个序列均以整型形式存储, 计算三个序列的CSN-2的文档大小及其压缩率。结果如表3所示。

表3 实验2三个序列的压缩率 Table 3 Experiment 2 compression ratio of three sequences

结论2:压缩率不受序列中整数大小顺序的影响。

3.2 CSN-2与哥德尔数的比较

在众多压缩算法中哥德尔数也是不依赖任何数据库的压缩方法, 因为原数据内容的不确定性, 所以原序列以整型序列进行了测试, 对比结果参见表4。在最坏情况下, 针对不同序列长度的实验结果如图1所示(计算机为32位)。

表4 CSN-2压缩数与哥德尔数的比较 Table 4 Compare CSN-2 compression numbers and Gö del numbers

	原整形序列	CSN-2压缩数	哥德尔数
存储内容	b_i, b_j, b_k, …, b_m整个序列	CSN-2一个数	一个数
空间利用率最坏情况 (长度为n的序列)	K· nbits(K为计算机字长)	log₂2(T+1)ⁿ-1bits	log₂ $\begin{matrix} 2^{b_{1}} \end{matrix}$ × $\begin{matrix} 3^{b_{2}} \end{matrix}$ × $\begin{matrix} 5^{b_{3}} \end{matrix}$ × …× $\begin{matrix} M^{b_{n}} \end{matrix}$ bits
空间利用率比较	$\begin{matrix} \begin{matrix} lo g_{2} 2 {(T + 1)}^{n} - 1 < K \cdot n < lo g_{2} 2^{b_{1}} \times 3^{b_{2}} \times 5^{b_{3}} \times \dots \times M^{b_{n}} & T < 2^{K} 且 n > 5 \end{matrix} \end{matrix}$

表4 CSN-2压缩数与哥德尔数的比较 Table 4 Compare CSN-2 compression numbers and Gö del numbers

	Figure Option View Download New Window
	图1 CSN-2压缩数与哥德尔数空间利用率比较Fig.1 CSN-2 compressed space utilization compared with Gö del number

由图1可知在CSN-2不同T情况下的空间压缩率是不相同的, 压缩率如表5所示。

表5 CSN-2压缩算法在不同T时的压缩率 Table 5 CSN-2 compression algorithm compression ratio at different thresholds

CSN-2压缩数通过对序列的重新计算得到与序列唯一对应的一个数, 通过存储压缩数来代替原序列, 节省较大的存储空间。哥德尔数也是通过对序列的重新计算得到的一个数, 但其仅对可计算函数集合具有压缩效果, 对其他类型的数据的压缩效率极低, 甚至超过原数据。

3.3 CSN-2与其他无损压缩算法的对比

因CSN-2的压缩结果与机器位数相关, 因此对于文档这种在压缩后的数会明显超过机器位数的数据进行处理时, 需要设计明确的分段标准。

由于CSN-2的压缩是一个递推过程, 因此可以随时查看其CSN-2压缩数的大小, 当压缩数超过机器位数时, 则停止此段压缩, 进而执行下一阶段的压缩。文中表6的测试过程就是通过此方法完成实现的。

表6 测试文档信息 Table 6 Test document information

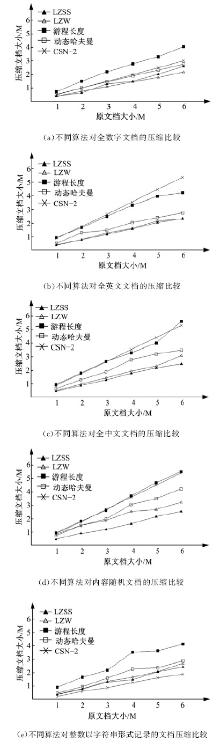
通过使用不同的压缩算法对表6中的30个文档进行压缩测试, 比较不同压缩算法的压缩率, 其结果如图2所示。其中压缩算法分别为LZSS、LZW、游程长度编码、动态哈夫曼编码和CSN-2压缩。

根据图2可知, CSN-2对以字符串形式记录整型数据文档的压缩效果最好, 对纯数字文档的压缩率也比较高。

	Figure Option View Download New Window
	图2 不同压缩算法压缩效率比较Fig.2 Compare the efficiency of different compression algorithms compress

因为常用的压缩软件WinRAR和WinZip都是采用多种压缩方案共存的形式, 针对不同类型的数据执行不同的压缩算法, 因此, 针对纯数字文档, 尤其是以字符串形式记录整型数据的文档进行压缩时, 可选择CSN-2压缩算法。

4 结束语

针对文档压缩进行了研究, 提出了CSN-1和CSN-2的存储方式, CSN-2通过对整型数据进行压缩, 使数据的空间复杂度降为O(log₂2(T+1)ⁿ-1)。通过解压算法可以找到对应的原数据, 实现数据还原。CSN-2的压缩不仅可以使其具有更高的空间利用率, 而且能够增加信息传递的可靠性。

通过CSN-2压缩的方式对文本进行压缩, 就是针对文本对应的ASCII码进行压缩。根据CSN-2针对字符串形式的整型数据压缩效率高的特点, 可以通过LZW等基于字典的压缩方案的主题思想进行改进, 即建立文档字典, 并对字典中每个字符串进行整型编码排序, 将文档以整型数组的形式记录下来, 最后通过CSN-2对文档的编码序号(整型数据)进行压缩。

CSN-2压缩方案具有较为广泛的应用范围, 例如环境温度的检测、心跳记录等。因为每种数据都具有其一定的取值范围, 如环境温度可视为-60℃~60℃, 人类心跳每分钟最快可达240次左右。因此每个数据没有必要使用一个INT(整型)数据来存储, 且这类数据具有局部聚合性, 因此通过CSN-2压缩方案进行压缩具有较高的压缩率。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	杨国为, 涂序彦, 庞杰. 基于虚拟信源的无损数据压缩方法研究[J]. 电子学报, 2003, 31(5): 728-731. Yang Guo-wei, Tu Xu-yan, Pang Jie. The research of lossless data compression based on a virtual information source[J]. Acta Electronica Sinica, 2003, 31(5): 728-731. [本文引用:1]
[2]	纪震, 周家锐, 朱泽轩, 等. 基于生物信息学特征的DNA 序列数据压缩算法[J]. 电子学报, 2011, 39(5): 991-995. Ji Zhen, Zhou Jia-rui, Zhu Ze-xuan, et al. Bioinformatics features based DNA sequence data compression algorithm[J]. Acta Electronica Sinica, 2011, 39(5): 991-995. [本文引用:1]
[3]	Chu D, Deshpand e A, Hellerstein J M, et al. Approximate data collection in sensor networks using probabilistic models[C]∥ICDE '06 Proceedings of the 22nd International Conference on Data Engineering, DC, 2006: 48-59. [本文引用:1]
[4]	Najafi H, Lahouti F, Shiva M. AR modeling for temporal extension of correlated sensor network data[C]∥Software in Telecommunications and Computer Networks, Split, 2006: 117-120. [本文引用:1]
[5]	Borgne Y L, Bontempi G. Unsupervised and supervised compression with principal component analysis in wireless sensor networks[C]∥Pro of the Workshop on Knowledge Discovery from Data, 13th ACM International Conference on Knowledge Discovery and Data Mining, New York, 2007: 94-103. [本文引用:1]
[6]	Ganesan D, Estrin D, Heidemann J. DIMENSIONS: Why do we need a new data hand ling architecture for sensor networks[J]. Acm Sigcomm Computer Communication Review, 2003, 33(1): 143-148. [本文引用:1]
[7]	郑翠芳. 几种常用无损数据压缩算法研究[J]. 计算机技术与发展, 2011, 21(9): 73-76. Zheng Cui-fang. Research of several common lossless data compression algorithms[J]. Computer Technology and Development, 2011, 21(9): 73-76. [本文引用:1]
[8]	Shannon C E. A mathematical theory of communication[J]. The Bell System Technical Journal, 1948, 27(7): 379-423. [本文引用:1]
[9]	Tsang P, Liu J P, Cheung K. Modern methods for fast generation of digital holograms[J]. 3D Research, 2010, 1(2): 11-18. [本文引用:1]
[10]	Wu J Z, Wang Y J, Ding L P, et al. Improving performance of network covert timing channel through Huffman coding[J]. Mathematical and Computer Modelling, In Press, Corrected Proof, 2011, 55(1): 69-79. [本文引用:2]
[11]	Jeong J, Jo J M. Adaptive Huffman coding of 2-D DCT coefficients for image sequence compression[J]. Signal Processing: Image Communication, 1995, 7(1): 1-11. [本文引用:1]
[12]	Rissanen J, Langdon G G. Universal modeling and coding[J]. Information Theory, 1981, 21(1): 12-23. [本文引用:1]
[13]	Miguel A, Prieto M, Adiego J. Natural language compression on Edge-Guided text preprocessing[J]. Information Sciences, 2011, 181(24): 5387-5411. [本文引用:2]
[14]	Freschi V, Bogliolo A. A faster algorithm for the computation of string convolutions using LZ78 parsing[J]. Information Processing Letters, 2010, 110(14-15): 609-613. [本文引用:1]
[15]	Arroyuelo D, Navarro G. Optimum string match choices in LZSS[J]. Information and Computation, 2011, 209(7): 1070-1102. [本文引用:1]
[16]	Lakhani G. Reducing coding redundancy in LZW[J]. Information Sciences, 2006, 176(10) : 1417-1434. [本文引用:2]
[17]	Gödel K. Über formal unentscheidbare Sätze der principia mathematica und verwand ter systeme[J]. Mathematics and Statistics, 1931, 38(1): 173-198. [本文引用:1]

2003

0.0

. 2003, 31(5):728-731 DOI:doi:10.3321/j.issn:0372-2112.2003.05.023

The research of lossless data compression based on a virtual information source

基于虚拟信源的无损数据压缩方法研究

Yang Guo-wei , Tu Xu-yan , Pang Jie.

杨国为, 涂序彦, 庞杰

本文首先提出了虚拟信源概念和基于虚拟信源构建数据压缩方法的思想,设立了0与1的字符长串的通用虚拟信源Y,然后用神经网络建立了虚拟信源Y的模型,又用该模型和一个取整函数构造出了基于虚拟信源的无损数据压缩方法.实验表明,一些情况下此压缩法的压缩比为3∶1.该压缩方法体现了虚拟信源建模思想,它与已有的熵编码(无损)压缩方法考察数据压缩问题的角度完全不同,它能压缩一些已用熵编码压缩过的数据.它与高保真的小波编码方法结合能获得一些高压缩比又高保真的数据压缩实例.

... 现有数据压缩算法分为有损压缩和无损压缩^[1] ...

2011

0.0

. 2011, 39(5):991-995 DOI:doi:http://ir.calis.edu.cn/hdl/244041/1333

Bioinformatics features based DNA sequence data compression algorithm

基于生物信息学特征的DNA 序列数据压缩算法

Ji Zhen , Zhou Jia-rui , Zhu Ze-xuan

纪震, 周家锐, 朱泽轩

A novel bioinformatics features based DNA Sequence data compression algorithm of BioLZMA is proposed in this paper.In BioLZMA,the DNA sequence data is sliced and reformed into 4 clusters according with biological meanings:the coding sequence cluster,the intron cluster,the RNA cluster and the residual cluster.By employing pointed compression strategies in data pre-processing,the clusters are compressed separately with LZMA algorithm.Experimental results demonstrated the better performance of BioLZMA than original DNA compression algorithms on benchmark sequences.Especially on long DNA sequence with significant bioinformatics features,BioLZMA algorithm can achieve higher compression ratio with little computation time.

本文通过将生物学特征和生物学含义引入DNA序列数据的压缩处理中,提出了基于生物信息学特征的BioLZMA压缩算法.在BioLZMA算法中,DNA序列根据组成部分生物学含义的不同切分重组为四个集合:编码序列CDS集合、内含子序列集合、RNA序列集合以及剩余序列的集合.根据各集合中序列的具体生物学特征分别使用针对性的压缩策略进行预处理,并通过LZMA算法进行压缩编码.实验结果表明,BioLZMA算法在基准测试序列上的压缩性能优于原有的DNA序列压缩方法.特别是对于生物信息学特征清晰的长序列,算法能够在较短的时间内获得较高的压缩率.

... 语音识别、医学和生物测量^[2]、股票价格、市场销售数据、气象数据、电信通信、传感器网络数据等均可采用有损压缩方法处理 ...

2006

0.0

... 有损压缩方法可分为基于概率模型^[3]、基于时间序列分析模型^[4]、基于数据挖掘模型^[5]、基于数据压缩模型^[6]这四类,其共性在于压缩率高,数据还原质量依赖于算法实现的代价 ...

2006

0.0

2007

0.0

2003

0.0

2011

0.0

. 2011, 21(9):73-76 DOI:doi:10.3969/j.issn.1673-629X.2011.09.019

Research of several common lossless data compression algorithms

几种常用无损数据压缩算法研究

Zheng Cui-fang.

郑翠芳

随着网络承载的信息量的飞速增长,数据压缩必然会备受人们重视.数据压缩可分成两种类型,一种叫做无损压缩,另一种叫做有损压缩.文中主要介绍目前用得最多和技术最成熟的无损数据压缩技术,按照无损压缩方法采用的压缩技术的不同,从基于统计的压缩思想和基于字典的压缩思想两个方面对其中最具有代表性的无损数据压缩方法进行了详细的分类讨论和优缺点比较,并对基于字典压缩算法的一些成熟的改进算法进行了汇总介绍,便于对无损数据压缩技术感兴趣的同志学习参考.

... 无损压缩技术^[7]在数据压缩过程中不允许损失精度,可以保真还原 ...

1948

0.0

... 香浓-凡诺算法^[8]由贝尔实验室开发,核心是构造一个通过叶子节点记录字符信息的二叉树,它是一种自顶向下的、非自适应的编码算法 ...

2010

0.0

... 游程长度编码(Run-Length-Coding)^[9]通过去除文本中的冗余字符或字节中的冗余位,达到减少数据文件所占的存储空间的目的,其压缩效能取决于整个数据流的重复字符出现次数、平均游程长度及所采用的编码结构 ...

2011

0.0

... Huffman编码是Huffman在1952年提出的一种基于信号概率的数据压缩算法^[10] ...

... 1978年提出的动态哈夫曼算法^[10,11]取消了统计过程,一边压缩一边动态调整哈夫曼树,提高了压缩效率 ...

1995

0.0

... 1978年提出的动态哈夫曼算法^[10,11]取消了统计过程,一边压缩一边动态调整哈夫曼树,提高了压缩效率 ...

1981

0.0

... 算术编码^[12]也是一种根据字符出现概率重新编码的压缩方案,该方法打破了哈夫曼算法必须用整数来表示字符的限制 ...

2011

0.0

... 主要算法包括:LZ77算法^[13]、LZ78算法^[14]、LZSS算法^[15]、LZW算法^[16]等 ...

... LZ77算法^[13]是第一个具有实用价值的基于词典编码的数据压缩算法,它利用一个窗口在原始数据中滑动,超前查看缓冲区中的刚刚由输入文件中读入的未编码字符,实现数据压缩、解压缩,也称为基于滑动窗口的自适应的字典压缩方法 ...

2010

0.0

... 主要算法包括:LZ77算法^[13]、LZ78算法^[14]、LZSS算法^[15]、LZW算法^[16]等 ...

2011

0.0

... 主要算法包括:LZ77算法^[13]、LZ78算法^[14]、LZSS算法^[15]、LZW算法^[16]等 ...

2006

0.0

... 主要算法包括:LZ77算法^[13]、LZ78算法^[14]、LZSS算法^[15]、LZW算法^[16]等 ...

... LZW算法^[16]是1984年Welch提出的基于LZ78算法的一个变种压缩算法 ...

1931

0.0

... del^[17]提出一种不依赖于数据库的无损压缩方法称为哥德尔数,但其使用范围局限于对图灵机程序的压缩,而不具有普遍性 ...