优化核参数的模糊C均值聚类算法

引用本文

刘云, 刘富, 侯涛, 张潇. 优化核参数的模糊C均值聚类算法. 吉林大学学报: 工学版, 2016, 46(1): 246-251
LIU Yun, LIU Fu, HOU Tao, ZHANG Xiao. Kernel-based fuzzy C-means clustering method based on parameter optimization. Journal of Jilin University Engineering and Technology Edition, 2016, 46(1): 246-251 复制到剪切板

Permissions

优化核参数的模糊C均值聚类算法

刘云, 刘富, 侯涛, 张潇

吉林大学通信工程学院,长春 130022

刘富(1968-),男,教授,博士生导师.研究方向:计算机视觉及模式识别.E-mail:liufu@jlu.edu.cn

作者简介:刘云(1989-),男,博士研究生.研究方向:模式识别及生物信息学.E-mail:582111845@qq.com

基金:吉林省重大科技攻关项目(20140204046); 国家自然科学基金项目(51105170)

摘要

核模糊C均值聚类算法(Kernel-based fuzzy C-means clustering method, KFCM)的性能受核参数的影响很大,然而实践中核参数的选择是极其困难的。为了解决这个问题,本文基于样本在高维空间中的类内距离近、而类间距离远这一思路,提出了一种优化核参数的模糊C均值算法(Parameter optimation-based KFCM, POKFCM)。该算法首先利用K均值方法对样本集进行初始聚类,再通过比较实际核函数矩阵与理想核函数矩阵的相似性距离来确定最优核参数,最后将优化的核参数应用于核模糊C均值聚类算法。在6组UCI数据集上进行对比实验,结果表明POKFCM能有效地改善KFCM的聚类性能。

关键词: 人工智能; 核模糊C均值; 核函数; 参数优化

中图分类号:TP391 文献标志码:A 文章编号:1671-5497(2016)01-0246-06

Kernel-based fuzzy C-means clustering method based on parameter optimization

LIU Yun, LIU Fu, HOU Tao, ZHANG Xiao

College of Communications Engineering, Jilin University, Changchun 130022, China

Abstract

Kernel-based Fuzzy C-means Clustering Method (KFCM) is a common method for data clustering. The performance of KFCM is greatly affected by the parameter of the kernel function, while the selection of kernel parameter is extremely difficult in practice. To solve this problem, a Parameter Optimization-based KFCM (POKFCM) is proposed according to the idea that the distances between samples of the same class are closer than the distance between samples from different classes. First, initial clustering of dataset is completed by K-means method. Then the optimal kernel parameter is determined by calculating the distance similarity between the actual kernel matrix and ideal kernel matrix. Finally, the optimal kernel parameter is applied to KFCM. Clustering experiment results of six UCI datasets illustrate that POKFCM can effectively improve the clustering performance of KFCM.

Keyword: artificial intelligence; kernel-based fuzzy C-means; kernel function; parameter optimization

Show Figures

0 引言

核模糊C均值算法(KFCM)是一种常用的聚类算法, 目前已被广泛应用于图像融合^{[1, 2]}、语音特征提取^[3]、非凸数据集分类^[4]、声音信号分类^[5]等方向。同时, 基于KFCM算法也开发了一些改进的算法, 如Liu等^[6]将属性均值聚类方法与KFCM相结合; Gu等^[7]将免疫遗传算法应用到KFCM中; Mohamed等^[8]在KFCM中用一种对噪声有抑制作用的距离测度代替欧式距离; Ferreira等^[9]在KFCM中引入了加权思想。

有研究结果表明, KFCM的聚类性能受核参数的影响很大, 选择不同核参数得到的聚类准确率往往相差较大, 甚至能高达50%以上^{[10, 11]}。同时, KFCM作为一种无监督学习的聚类方法, 由于不存在学习样本的先验知识, 使得核参数的选择极其困难。目前已有的几种的核参数优化方法都是在迭代循环中引入优化准则, 如:Chen和Li等^{[12, 13]}利用了Fisher准则来优化核参数; Na等^[14]将ML(Must link)和CL(Cannot link)两个约束引入到了核模糊C均值方法的代价函数中, 在最小化代价函数的过程中, 同时优化隶属度矩阵和核参数。然而, 这些方法的聚类过程都繁琐且复杂。

为了解决这个难题, 本文提出了一种优化核参数的模糊C均值算法(POKFCM), 该算法首先利用K均值算法对数据集进行初始聚类; 其次, 利用初始聚类的结果构建理想的核函数矩阵, 通过最小化其与实际核函数矩阵的距离相似性测度来进行参数优化; 最后, 将优化的核参数应用于核模糊C均值聚类算法。为了验证该方法的性能, 在UCI数据库中下载了6个连续数据集, 在这些数据集上进行对比实验, 结果表明POKFCM能有效地改善KFCM的聚类性能。

1 KFCM简述

KFCM是将核函数与模糊C均值方法相结合, 用以解决数据集的线性不可分问题。

对于一个给定数据集X={x₁, x₂, …, x_N}, KFCM算法的核心思想是利用非线性映射φ 将其映射到高维空间φ (X)={φ (x₁), φ (x₂), …, φ (x_N)}, 在高维空间中利用模糊C均值进行聚类分析。为了避免在高维空间中计算特征向量之间的内积而引发的“ 维数灾难” , KFCM算法利用核函数计算样本在高维空间中的内积。最后通过最小化目标函数将数据集X分为k个聚类, 使得同类之间相似性尽可能高、异类之间相似性尽可能低^[9]。

KFCM的目标函数如式(1)所示:

$\begin{matrix} J (U, θ) = \overset{N}{\sum_{i = 1}} \overset{k}{\sum_{j = 1}} (u_{ij})^{q} d (φ (x_{i}), θ_{j}) (1) \end{matrix}$

式中:N为样本数量; k为聚类个数; q(> 1)为模糊度; d $\begin{matrix} (φ (x_{i}), θ_{j}) \end{matrix}$ 代表高维空间中第i个样本φ (x_i)与第j个聚类中心θ _j之间的距离测度。其中隶属度矩阵U中元素u_ij满足如下约束条件:

$\begin{matrix} \overset{k}{\sum_{j = 1}} u_{ij} = 1, u_{ij} \in [0, 1] (2) \end{matrix}$

KFCM的聚类中心为:

$\begin{matrix} θ_{j} = \frac{\overset{N}{\sum_{i = 1}} u_{ij}^{q} φ (x_{i})}{\overset{N}{\sum_{i = 1}} u_{ij}^{q}} (3) \end{matrix}$

最小化目标函数可以通过令其对隶属度矩阵U的偏导数为零来实现:

$\begin{matrix} \frac{\partial J (U, θ)}{\partial U} = 0 (4) \end{matrix}$

方程(4)的解为:

$\begin{matrix} \begin{matrix} u_{rs} = {(\frac{\overset{k}{\sum_{j = 1}} d (φ (x_{r}), θ_{j})}{d (φ (x_{r}), θ_{s})})}^{\frac{1}{q - 1}} \\ r = 1, 2, \dots, N; s = 1, 2, \dots, k (5) \end{matrix} \end{matrix}$

结合式(3)(5)不断地循环优化隶属度矩阵U, 直到得到满意的结果。最后去模糊化得到最终的聚类结果。传统的核模糊C均值算法不涉及核参数的优化。

2 优化核参数的KFCM(POKFCM)

本文的优化核参数的模糊C均值算法主要分为3步:首先利用K均值聚类构建一个学习样本, 然后根据这个学习样本优化核参数, 最后再利用优化的核参数完成对数据集的核模糊C均值聚类。

2.1 K均值聚类

对于一个给定数据集X={x₁, x₂, …, x_N}, 首先利用K均值聚类进行初始聚类估计, 将其分为K类。经过K均值聚类, 可得到一个N维行向量L, 其中元素的值L_i代表相应样本的归属, 如式(6)所示:

$\begin{matrix} L_{i} = k', 1 \leq k' \leq k, i = 1, 2, \dots, N (6) \end{matrix}$

满足d(x_i, θ _k')< $\begin{matrix} \min_{j = 1, 2, \dots, k, j \neq k'} \end{matrix}$ d(x_i, θ _j), 代表样本x_i属于第k'类。

2.2 核函数参数优化

对于数据集X, 可以用如下核函数矩阵

$\begin{matrix} K = {(k_{ij})}_{N \times N} = {(k (x_{i}, x_{j}))}_{N \times N} (7) \end{matrix}$

来表示特征向量之间在高维空间中的内积, k_ij即为样本x_i与x_j在高维空间中的内积。核函数矩阵K是一个对称矩阵。

本文选用径向基核函数:

$\begin{matrix} k (x, y) = \exp (- \frac{‖ x - y ‖^{2}}{2 σ_{}^{2}}) (8) \end{matrix}$

式中:‖ · ‖ 代表向量间的欧氏距离; σ 为待优化的参数。由式(8)可知, 径向基核函数值的取值范围为[0, 1]。因此, 根据同类样本之间距离尽可能近、异类样本之间距离尽可能远的思路^[15], 可以构造一个理想的核函数矩阵:

$\begin{matrix} k_{ij} = \{\begin{matrix} 1, L_{i} = L_{j} \\ 0, L_{i} \neq L_{j} \end{matrix} (9) \end{matrix}$

而实际的核矩阵为:

$\begin{matrix} k'_{ij} = \exp (- \frac{‖ x_{i} - x_{j} ‖^{2}}{2 σ^{2}}) (10) \end{matrix}$

它是一个关于核参数σ 的对称函数矩阵, 主对角线上元素为1。因此, 核参数的优化问题就转化成了实际的核函数矩阵与上述理想核矩阵的相似度问题。

本文采用基于欧式距离的测度来衡量理想核函数矩阵与实际核函数矩阵的相似度:

$\begin{matrix} E (K, K') = \overset{N}{\sum_{i = 1}} \overset{N}{\sum_{j = 1}} {(k_{ij} - k'_{ij})}^{2} (11) \end{matrix}$

式中:K代表理想的核函数矩阵; K'代表样本实际的核函数矩阵。E(K, K')代表两个矩阵对应元素差值的平方和, 是关于核参数σ 的函数。因此, 核参数的优化问题就转化成了计算E(K, K')的最小值的问题, 令其关于σ 的导数为零:

$\begin{matrix} \frac{\partial E (K, K')}{\partial σ} = 0 (12) \end{matrix}$

求解方程(12)即可求得最优的核参数σ ₀。

2.3 优化核参数的核模糊C均值算法及其复杂度

将2.2节中的优化方法所求的核参数σ ₀带入式(8)可得到优化的径向基核函数:

$\begin{matrix} k_{0} (x, y) = \exp (- \frac{‖ x - y ‖^{2}}{2 σ_{0}^{2}}) (13) \end{matrix}$

将式(13)带入式(5), 即可得到核模糊C均值方法的迭代公式:

$\begin{matrix} \begin{matrix} u_{rs}^{(t)} = {(\frac{\overset{k}{\sum_{j = 1}} d (φ (x_{r}), \frac{\overset{N}{\sum_{i = 1}} {(u_{ij}^{(t - 1)})}^{q} φ (x_{i})}{\overset{N}{\sum_{i = 1}} {(u_{ij}^{(t - 1)})}^{q}})}{d (φ (x_{r}), \frac{\overset{N}{\sum_{i = 1}} {(u_{ir}^{(t - 1)})}^{q} φ (x_{i})}{\overset{N}{\sum_{i = 1}} {(u_{ir}^{(t - 1)})}^{q}})})}^{\frac{1}{q - 1}} = \\ {(\frac{\overset{k}{\sum_{j = 1}} \frac{\overset{N}{\sum_{i = 1}} {(u_{ij}^{(t - 1)})}^{q} d (φ (x_{r}), φ (x_{i}))}{\overset{N}{\sum_{i = 1}} {(u_{ij}^{(t - 1)})}^{q}}}{\frac{\overset{N}{\sum_{i = 1}} {(u_{ir}^{(t - 1)})}^{q} d (φ (x_{r}), φ (x_{i}))}{\overset{N}{\sum_{i = 1}} {(u_{ir}^{(t - 1)})}^{q}}})}^{\frac{1}{q - 1}} (14) \end{matrix} \end{matrix}$

式中: $\begin{matrix} u_{ij}^{(t - 1)} \end{matrix}$ 为上一次循环的隶属度矩阵; $\begin{matrix} u_{rs}^{(t)} \end{matrix}$ 为当前循环的隶属度矩阵。式(14)中的样本在高维空间中的距离为:

$\begin{matrix} \begin{matrix} d (φ (x_{r}), φ (x_{i})) = \\ \sqrt[]{k_{0} (x_{r}, x_{r}) - 2 k_{0} (x_{r}, x_{i}) + k_{0} (x_{i}, x_{i})} \\ (15) \end{matrix} \end{matrix}$

综上, 优化核参数的核模糊C均值算法(POKFCM)的步骤可以总结如下:

(1)根据第2.1节和2.2节的方法求得数据集X的最优核参数。

(2)给定核模糊C均值算法的初始条件, 如聚类数k, 最小迭代误差e, 模糊度q, 初始隶属度矩阵U⁽⁰⁾和最大迭代次数n。

(3)根据式(14)(15)更新隶属度矩阵, 直到‖ U⁽^t⁾-U⁽^t-¹⁾‖ ≤ e或者迭代次数≥ n。

(4)去模糊化得到聚类结果。

本文算法的时间消耗主要集中在核参数优化过程中。算法的计算复杂度为T(n)=o(4n²)。

3 实验结果

3.1 实验数据

为了验证本文算法的性能, 从UCI数据库(http://archive.ics.uci.edu/ml/)下载了6个数据集Iris、Wine、Seed、User knowledge modeling、Libras movement和Pengidits, 具体信息如表1所示。在这些数据集上进行聚类分析, 以验证本文算法的性能。

表1 本文选用的数据集信息 Table 1 Information of selected datasets in this paper

3.2 核参数对KFCM性能的影响

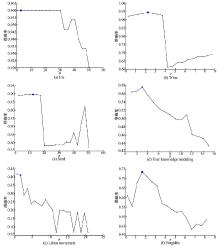
图1表示6个数据集在不同核参数下的聚类效果。本文中用聚类准确率来衡量算法的聚类效果, 聚类准确率为正确聚类的样本数量占总样本数量的百分比。由图1可知, 不同的核参数对于聚类效果有很大的影响, 尤其对于数据集Wine和Pendigits, 最好的结果与最差的结果相差都在30%左右。

	Figure Option View Download New Window
	图1 不同核参数下各个数据集的聚类效果Fig.1 Clustering result of each dataset with different kernel parameter

图1中放大的点代表优化后的σ 对应的聚类准确率。从这6幅图中可以看出, 采用优化后的核参数都能得到最优的聚类效果。唯一例外的是图1(e), 其优化后的核参数σ 并非最优的核参数, 而是次优的, 然而其准确率仅比最优的核参数对应的准确率小1%, 这并不影响本文方法的优化效果。

3.3 POKFCM的聚类效果

对上述6组实验数据集, 用本文POKFCM算法和传统的KFCM算法分别对其进行聚类分析, 结果如表2所示。由表2可知, 对本文所用的6个数据集, POKFCM算法的准确率均高于传统的KFCM算法与初始的K均值聚类算法。尤其对于数据集User knowledge modeling, POKFCM的准确率比KFCM方法高12%。

表2 POKFCM的聚类效果 Table 2 Clustering performance of POKFCM

表3为本文POKFCM算法与文献[14]和文献[16]所提算法进行对比的试验结果。文献[14]和文献[16]提出了两种不同的核聚类中参数优化的方法, 并将其运用到模糊C均值方法中, 与本文有相同的思路, 因此, 他们的实验结果可以用来与本文进行对比。由表3可知, 对于数据集Iris和Wine, 结果显示本文方法的准确率高于文献[14], 尤其对于数据集Wine, 本文POKFCM算法的准确率比文献[14]高26%; 对于数据集Iris和Pendigits, 本文POKFCM算法的准确率均高于文献[16]的方法。

表3 本文算法与文献[14][16]的对比结果 Table 3 Result comparison among proposed method and ref.[14] and [16]

4 结束语

为了解决核模糊C均值聚类方法中核参数的选择问题, 本文提出了一种优化核参数的模糊C均值算法POKFCM。首先, 利用K均值聚类方法对数据集进行初始聚类; 其次, 构建理想的核函数矩阵与实际的核函数矩阵, 并通过使实际核函数矩阵尽可能地接近理想核函数矩阵的方法计算最优的核参数; 最后, 利用优化的核参数完成核模糊C均值聚类。对不同的数据集进行聚类的实验结果表明, 本文所提的优化方法能找到最优的核参数, 从而一定程度上改善了传统核模糊C均值算法(KFCM)的性能。与文献[14][16]相比, 本文算法也具有一定的优越性。然而, 本文算法的一个局限性是核参数的优化结果依赖于初始聚类的准确率。因此, 如何减弱这种依赖, 研究鲁棒性更强的优化方法将是下一步的主要工作。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Chen L, Lu M, Chen C L P, et al. Multiple kernel fuzzy C-means based image segmentation[C]∥IEEE International Conference on Systems, Man and Cybernetics, Istanbul, 2010: 4123-4129. [本文引用:1]
[2]	Gong M, Liang Y, Shi J, et al. Fuzzy C-means clustering with local information and kernel metric for image segmentation[J]. IEEE Transactions on Image Processing, 2013, 22(2): 573-584. [本文引用:1]
[3]	Zhang J. Speech feature extraction of KPCA based on kernel fuzzy K-means clustering[C]∥IEEE International Conference on Computer Science and Service System (CSSS), Nanjing, 2011: 756-759. [本文引用:1]
[4]	叶吉祥, 谭冠政, 路秋静. 基于核的非凸数据模糊C均值聚类研究[J]. 计算机工程与设计, 2005, 26(7): 1784-1786. Ye Ji-xiang, Tan Guan-zheng, Lu, Qiu-jing. Fuzzy C-means clustering algorithm to non-spherical shape data based on kernel[J]. Computer Engineering and Design, 2005, 26(7): 1784-1786. [本文引用:1]
[5]	Park D C. Classification of audio signals using fuzzy C-means with divergence-based kernel[J]. Pattern Recognition Letters, 2009, 30(9): 794-798. [本文引用:1]
[6]	Liu J, Xu M. Kernelized fuzzy attribute C-means clustering algorithm[J]. Fuzzy Sets and Systems, 2008, 159(18): 2428-2445. [本文引用:1]
[7]	Gu C, Zhang S, Liu K, et al. Fuzzy kernel K-means clustering method based on immune genetic algorithm[J]. Journal of Computational Information Systems, 2011, 7(1): 221-231. [本文引用:1]
[8]	Mohamed B, Ahmed T, Lassad H, et al. A new extension of fuzzy C-Means algorithm using non Euclidean distance and kernel methods[C]∥International Conference on Control, Decision and Information Technologies (CoDIT), Hammamet, 2013: 242-249. [本文引用:1]
[9]	Ferreira M R P, de Carvalho F D A T. Kernel fuzzy C-means with automatic variable weighting[J]. Fuzzy Sets and Systems, 2014, 237: 1-46. [本文引用:2]
[10]	Graves D, Pedrycz W. Fuzzy C-means, Gustafson-Kessel FCM, kernel-based FCM: a comparative study[J]. Advances in Soft Computing, 2007, 41: 140-149. [本文引用:1]
[11]	Graves D, Pedrycz W. Kernel-based fuzzy clustering and fuzzy clustering: a comparative experimental study[J]. Fuzzy Sets and Systems, 2010, 161(4): 522-543. [本文引用:1]
[12]	Chen B, Liu H, Bao Z. A kernel optimization method based on the localized kernel Fisher criterion[J]. Pattern Recognition, 2008, 41(3): 1098-1109. [本文引用:1]
[13]	Li J B, Wang Y H, Chu S C, et al. Kernel self-optimization learning for kernel-based feature extraction and recognition[J]. Information Sciences, 2014, 257: 70-80. [本文引用:1]
[14]	Na W, Xia L. Kernel parameter optimization for semi-supervised fuzzy clustering with pairwise constraints[J]. Chinese Journal of Electronics, 2008, 17(2): 2007-2010. [本文引用:1]
[15]	李晓宇, 张新峰, 沈兰荪. 一种确定径向基核函数参数的方法[J]. 电子学报, 2005, 33(12): 2459-2463. Li Xiao-yu, Zhang Xin-feng, Shen Lan-sun. A selection means on the parameter of radius basis function[J]. Acta Electronica Sinica, 2005, 33(12): 2459-2463. [本文引用:1]
[16]	Zhang H, Lu J. Semi-supervised fuzzy clustering: a kernel-based approach[J]. Knowledge-Based Systems, 2009, 22(6): 477-481. [本文引用:1]

2010

0.0

... 0 引言核模糊C均值算法(KFCM)是一种常用的聚类算法,目前已被广泛应用于图像融合^[1,2]、语音特征提取^[3]、非凸数据集分类^[4]、声音信号分类^[5]等方向 ...

2013

0.0

2011

0.0

2005

0.0

2009

0.0

2008

0.0

... 同时,基于KFCM算法也开发了一些改进的算法,如Liu等^[6]将属性均值聚类方法与KFCM相结合 ...

2011

0.0

... Gu等^[7]将免疫遗传算法应用到KFCM中 ...

2013

0.0

... Mohamed等^[8]在KFCM中用一种对噪声有抑制作用的距离测度代替欧式距离 ...

2014

0.0

... Ferreira等^[9]在KFCM中引入了加权思想 ...

... 最后通过最小化目标函数将数据集X分为k个聚类,使得同类之间相似性尽可能高、异类之间相似性尽可能低^[9] ...

2007

0.0

... 有研究结果表明,KFCM的聚类性能受核参数的影响很大,选择不同核参数得到的聚类准确率往往相差较大,甚至能高达50%以上^[10,11] ...

2010

0.0

... 有研究结果表明,KFCM的聚类性能受核参数的影响很大,选择不同核参数得到的聚类准确率往往相差较大,甚至能高达50%以上^[10,11] ...

2008

0.0

... 目前已有的几种的核参数优化方法都是在迭代循环中引入优化准则,如:Chen和Li等^[12,13]利用了Fisher准则来优化核参数 ...

2014

0.0

... 目前已有的几种的核参数优化方法都是在迭代循环中引入优化准则,如:Chen和Li等^[12,13]利用了Fisher准则来优化核参数 ...

2008

0.0

... Na等^[14]将ML(Must link)和CL(Cannot link)两个约束引入到了核模糊C均值方法的代价函数中,在最小化代价函数的过程中,同时优化隶属度矩阵和核参数 ...

2005

0.0

... 因此,根据同类样本之间距离尽可能近、异类样本之间距离尽可能远的思路^[15],可以构造一个理想的核函数矩阵: ...

2009

0.0