分类学习包括两个阶段, 分别是学习阶段和分类阶段。在学习阶段, 根据训练样本学习一个或一组样本属性与预定义类别相关的分类器, 在分类阶段, 根据学习到的分类器, 按照未知类别样本的属性特征将其划分到预定义的类别中。根据分类算法学习到的分类器是否具有可理解性, 可以分为分类器不可理解和分类器可理解两类算法, 神经网络方法、支持向量机方法^[1]属于前者, 这类方法学习到一个难以理解的复杂的数学函数; 决策树学习^[2]属于后者, 学习到一组人类可以理解的分类规则。很多实际的分类任务需要学习到的分类器具有可理解性, 进而领域专家可在分类器基础上进行验证和调整。

分类器可理解的分类方法主要分为并行覆盖方法和序列覆盖方法两类。并行覆盖方法一次性学习出所有的分类规则, 如决策树学习, 采用贪婪方法从训练样本中学习一颗决策树, 该方法在建树过程中不进行回溯, 容易收敛到局部最优解。序列覆盖方法一次学习一个精确度最好的分类规则, 以递增的方式学习有序规则集合, 由于蚁群算法和粒子群算法等元启发式方法能够有效求解优化问题, 并具有自适应性强、鲁棒性好等优点, 因此基于元启发式方法的序列覆盖算法近年来受到研究者的关注。基于蚁群系统的分类算法AntMiner^[3]是第一个用蚁群优化思想来求解分类问题的方法, 该方法定义了与分类问题相关的启发式信息和信息素更新模型, 从而解决分类问题。为提高AntMiner算法的性能, AntMiner+^[4]算法对AntMiner进行了改进和扩展, 主要从所采用的基础蚁群算法、启发式规则设计、信息素更新函数、规则评价函数等方面进行了改进。PSO/ACO2^[5]是粒子群优化和蚁群优化相结合的混合分类算法, 两种优化方法的结合使得该算法可以有效处理离散和连续的属性。文献[6]提出一种基于蜂群优化的分类方法, 可以有效处理连续属性, 但无法处理离散属性。实际分类问题中通常同时包括离散属性和连续属性, 因此分类算法能兼顾离散属性和连续属性的处理, 对于分类性能至关重要。

序列覆盖算法采用规则评价函数来评价规则的优劣, 文献[7-9]总结了几种常用的规则评价函数如Klosgen、F-measure、Reletive cost measure和M-estimate等, 现有的基于元启发式方法的序列覆盖算法均是固定某一个规则评价函数, 而从文献[7-9]中对比实验可知, 给定一个序列覆盖算法, 在同一数据集上, 采用不同的规则评价函数算法性能也各不相同; 同时, 针对不同的数据集, 不存在一个规则评价函数能在所有数据集上性能都最优。由此可见, 序列覆盖算法中如果固定了一个规则评价函数, 将不能保证在所有数据集上都取得较好的效果。

本文以人工蜂群优化算法为基础, 根据离散属性和连续属性的特点设计雇佣蜂、观察蜂和侦察蜂的觅食策略, 使得算法能够有效处理连续类型和离散类型的属性; 同时, 研究如何为不同数据集自适应选取相适应的规则评价函数, 从而实现求解分类问题的自适应人工蜂群算法, 提高分类的准确率。

人工蜂群算法^[10]源于对蜂群内部分工机制及其觅食行为的模拟, 已被广泛应用于求解多种优化问题, 具有收敛速度快和鲁棒性好等特点。

蜂群优化模型中包含3个基本要素:食物源、受雇佣的觅食者、非受雇佣的觅食者。食物源表示待优化问题的一个可行解, 食物源的丰富程度代表解的质量即适应度。受雇佣的觅食者即雇佣蜂与一个特定的食物源相关联, 携带这个食物源的相关信息, 并以一定的概率共享这些信息。非受雇佣的觅食者包括侦察蜂和观察蜂两种, 侦察蜂主要负责在蜂巢周围搜寻新的食物源, 当雇佣蜂进行一定次数(limit)的搜索之后发现食物源的质量并没有提高时会变成一只侦察蜂; 观察蜂根据雇佣蜂分享的食物源信息按照一定的概率选择雇佣蜂进行跟随, 食物源被侦察蜂选择的概率计算公式如下:

Pi=fiti∑k=1SNfitk1

式中:fit_i表示第i个食物源的适应度; SN表示食物源的数量, 也是雇佣蜂的数量。

为了找到更好的食物源, 雇佣蜂会在绑定的食物源周围进行邻域搜索, 同样的, 观察蜂选定一个食物源X_i后也会进行邻域搜索, 式(2)是一种邻域搜索策略。

Vij=Xij+Φij(Xij-Xkj)(2)

式中:X_i表示当前食物源; V_i表示邻居食物源; j是一个随机索引, 表示修改食物源X_i的第j维元素; Φ _ij是一个[-1, 1]区间内的随机数, 控制V_ij在X_ij的邻域; k是一个不同于i的随机数。算法会采用贪婪选取方法比较食物源V_i和X_i的适应度, 如果新食物源V_i优于X_i, 则让V_i取代X_i, 否则X_i被保留不变。

自适应人工蜂群分类算法的目标是有效处理离散属性和连续属性, 并为不同数据集自适应选取相适应的规则评价函数, 以提高分类性能。自适应人工蜂群算法利用动态分配资源即雇佣蜂的方法, 在算法运行过程中对采用不同规则评价函数所生成的食物源进行比较和选择, 为较优的规则评价函数分配更多的资源, 同时减少其他规则评价函数对应的资源, 当资源数为零时则淘汰相应的规则评价函数, 这一过程不断迭代, 直至最终得到一个性能最优的规则评价函数和相应的分类规则集。

为验证自适应人工蜂群算法(A_ABC)的有效性, 本节首先探讨算法重要参数设置问题, 然后在公共数据集上将A_ABC与相关算法进行性能对比。共选取了6组数据集^[11], 基本信息如表1所示。

表1

Table 1

表1(Table 1)

表1 测试数据集简介 Table 1 Testing dataset introduction 数据集名称 是否二 元分类 属性类型 样例个数 属性 个数 SONAR 是 数值型 208 60 Tic-Tac-Toe(TTT) 是 命名型 958 9 Balance 否 整数型 625 4 Contraceptive method choice(CMC) 否 混合型 1473 9 Chess-King-Rook(CKR) 是 命名型 3196 36 Flags 否 混合型 194 30

表1 测试数据集简介 Table 1 Testing dataset introduction

二元分类表示类别为“ 是/否” 的形式, 而非二元分类的类别则超过两种。属性类型中, 数值型和整数型为连续类型, 命名型则为离散类型, 混合型则既有连续类型也有离散类型。

实验1 参数设置

自适应人工蜂群算法中包含多个参数, 具体有蜂群算法基本参数Csize、limit和MCN, 规则评价函数中参数ω 、γ 和m以及自适应人工蜂群算法特有的资源重分配参数step。根据经验将Csize和MCN分别设置为50和2000。规则评价函数中参数ω 、γ 和m的设置与算法准确率间关系在文献[7]中有详尽的实验, 此处, 采取结果较优的参数设置, 即ω =0.40、γ =0.25、m=4。参数limit表示食物源质量连续limit次没有提高, 将被放弃。该参数设置的优劣直接决定算法的全局搜索能力; 参数step代表每次资源调整的幅度, 如果设置的不好, 算法会过早收敛到某个规则评价函数上, 这将导致一个次优的规则评价函数可能会占据大多数的资源, 从而导致其他更好的规则评价函数没能够得到表现。

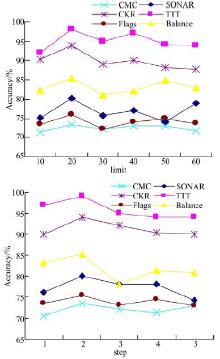
本文为每一个参数设定了一个合理的候选取值范围, 如表2所示。在讨论任一参数对算法的影响时, 固定其他参数的取值, 对于已讨论过的参数, 其值设置为取值范围内统计结果最佳值; 对于尚未讨论的参数其值取中间值。针对参数limit和step, 取不同值在各数据集上运行10次, 算法终止条件为找出最优规则评价函数(其余规则评价函数全部淘汰), 并且未被覆盖的训练样例数少于5%, 最终10次运行结果的平均值作为算法的最终准确率, 结果如图1所示。

表2

Table 2

表2(Table 2)

表2 参数取值范围表 Table 2 Turned parameters 参数 默认值 取值范围 limit 35 [10, 20, …, 60] step 3 [1, 2, …, 5]

表2 参数取值范围表 Table 2 Turned parameters

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 参数设置结果图Fig.1 Parameter setting result

参数的不同取值对算法性能的影响较大, 其中limit=20和step=2, 从统计意义上来讲是一种相对较好的设置。

实验2 分类算法性能对比

将分类器不可理解的Kalman Filter+SVM算法^[1]、分类器可理解的WrapTree^[2]、Antminer+^[4]和PSO/ACO2^[5]算法, 与本文提出的自适应人工蜂群算法A_ABC进行性能对比, 同时为说明规则评价函数对算法性能的影响, 将Antminer+算法分别固定Klosgen、F-measure、M-estimate和Q⁺四种规则评价函数进行性能测试, 算法的参数和终止条件与实验1相同, 其他对比算法除终止条件外保留原始研究中的参数设置不变。最终实验结果分别如表3和表4所示。表中“ REF” 表示A_ABC算法自适应选择的规则评价函数, “ Acc” 表示算法的正确率, “ #RN” 表示规则条数, “ #AAC” 表示平均每条规则所包含的语句数(即属性值约束的数量)。

表3

Table 3

表3(Table 3)

表3 分类算法性能对比实验 Table 3 Performance comparison among classification algorithms 算法 SONAR Tic-Tac-Toe Balance REF Acc/% #RN #AAC REF Acc/% #RN #AAC REF Acc/% #RN #AAC A_ABC Klosgen 80.52 10 4.16 Q+ 99.29 5 3 M-estimate 85.06 32 3.23 Antminer+(Klosgen) 68.27 5 3.2 99.27 7 2.86 69.28 5 1.8 Antminer+(F-measure) 72.12 5 2.8 99.16 5 2.8 70.08 6 2 Antminer+(M-estimate) 70.67 4 2.8 98.54 8 3 75.20 14 2.21 Antminer+(Q+) 71.63 8 2.75 99.27 6 3.17 51.20 7 3 PSO/ACO2 77.08 5 2.6 99.35 9 2.67 82.71 27 2.56 WrapTree 71.42 16 83.94 78 76.93 28 Kalman Filter+SVM 75.28 92.12 89.84

表3 分类算法性能对比实验 Table 3 Performance comparison among classification algorithms

表4

Table 4

表4(Table 4)

表4 分类算法性能对比实验(续) Table 4 Performance comparison among classification algorithms 算法 Contraceptive method choice Chess-King-Rook Flags REF Acc/% #RN #AAC REF Acc/% #RN #AAC REF Acc/% #RN #AAC A_ABC Klosgen 74.82 67 4.87 F-measure 94.63 10 4 Klosgen 76.15 34 7.39 Antminer+(Klosgen) 58.45 42 4.42 93.71 9 3.78 65.98 7 2.14 Antminer+(F-measure) 56.82 42 4.33 91.71 12 4.25 61.34 9 2.44 Antminer+(M-estimate) 61.64 97 4.86 94.43 10 3.8 60.82 7 2.57 Antminer+(Q+) 63.61 195 5.25 89.27 10 3.7 62.89 17 7.24 PSO/ACO2 74.58 83 4.76 93.46 13 3.74 64.25 28 5.37 WrapTree 60.92 79 90.86 49 61.84 32 Kalman Filter+ SVM 63.53 91.76 65.52

表4 分类算法性能对比实验(续) Table 4 Performance comparison among classification algorithms

首先, 从Antminer+算法(分别固定4种规则评价函数)在各个数据集上的测试结果可以看出, 针对同一个数据集, Antminer+算法随采用规则评价函数的不同, 算法性能也不同, 并且不存在一个规则评价函数, 能够使得Antminer+算法在所有数据集上性能都最优; 其次, 从A_ABC算法在各个数据集上的运行结果可以看出, 针对不同数据集A_ABC算法所选取规则评价函数也不尽相同; 最后, 从5种算法的总体运行结果来看, 在Balance数据集上Kalman Filter+SVM算法性能明显优于其他算法, 在SONAR、Contraceptive method choice和Flags数据集上A_ABC算法执行正确率明显优于其他算法, 在Tic-Tac-Toe数据集上A_ABC和Antminer+算法的正确率相当, 在Chess-King-Rook数据集上A_ABC、PSO/ACO2和Antminer+(M-estimate)算法的正确率相当。总体上, 在分类器可理解的分类算法中, A_ABC算法的性能较好, 原因在于A_ABC算法能够为各个数据集自适应选出相适应的规则评价函数并能有效处理连续类型的属性, 使得A_ABC算法具有更好的性能和适用性。

本文针对现有基于元启发式优化方法的分类算法存在的问题, 提出一种求解分类问题的自适应人工蜂群算法, 能够为不同数据集自适应选取相适应的规则评价函数, 同时能够有效处理连续属性和离散属性, 实验结果证明了本文算法的有效性。