基于局部邻域约束的空间验证方法

引用本文

赵宏伟, 李清亮, 汤寰宇, 臧雪柏. 基于局部邻域约束的空间验证方法. 吉林大学学报: 工学版, 2016, 46(1): 265-270
ZHAO Hong-wei, LI Qing-liang, TANG Huan-yu, ZANG Xue-bai. Spatial verification method based on local regional constraint. Journal of Jilin University Engineering and Technology Edition, 2016, 46(1): 265-270 复制到剪切板

Permissions

基于局部邻域约束的空间验证方法

赵宏伟^1,², 李清亮¹, 汤寰宇¹, 臧雪柏¹

1.吉林大学计算机科学与技术学院,长春 130012

2.吉林大学符号计算与知识工程教育部重点实验室,长春 130012

臧雪柏(1963-),女,研究员,博士.研究方向:智能信息系统.E-mail:zangxb@jlu.edu.cn

作者简介:赵宏伟(1962-),男,教授,博士生导师.研究方向:智能信息系统与嵌入式技术.E-mail:zhaohw@jlu.edu.cn

基金:国家自然科学基金项目(61101155); 吉林省自然科学基金项目(201215045,20140101184JC)

摘要

提出了用基于局部邻域约束的空间验证方法去验证错误的匹配特征。首先,计算匹配特征对的局部邻域范围,根据局部邻域内相关匹配特征对的数量定义该匹配对的局部邻域约束值,并判断是否满足局部邻域的约束条件。若满足,则基于局部邻域内的所有相关匹配特征的排列顺序,验证其是否满足一致的几何变换关系。实验结果表明:SVLRC方法具有较低的时间复杂度,改善了最终检索结果的精确度。

关键词: 计算机应用; 图像检索; Bag of Words模型; 局部邻域; 空间约束; 后验证

中图分类号:TP391.41 文献标志码:A 文章编号:1671-5497(2016)01-0265-06

Spatial verification method based on local regional constraint

ZHAO Hong-wei^1,², LI Qing-liang¹, TANG Huan-yu¹, ZANG Xue-bai¹

1.College of Computer Science and Technology, Jilin University, Changchun 130012,China

2.Key Laboratory of Symbolic Computation and Knowledge Engineering of Ministry of Education, Jilin University, Changchun 130012, China

Abstract

A Spatial Verification method based on Local Regional Constraints (SVLRC) is developed to remove false positive matches. First, the local region range of a center match pair is calculated. Then, the constraint value of the centre matches is defined according to the number of other matches in the local regions and whether the center match pairs satisfy the condition of local region constraint is judged. If the condition is met, whether all the matches in the local regions follow consistent geometric transformation is estimated based on geometric order. Extensive experiments demonstrate that the SVLRC can improve the retrieval accuracy significantly with low computation cost.

Keyword: computer application; image retrieval; Bag of Words model; local regions; spatial constraint; post-processing

Show Figures

0 引言

随着多媒体信息的迅速发展, 图像检索技术已成为研究热点^{[1, 2]}, 然而大多数图像检索系统都是基于Bag of Words(BoW)模型^[3]实现, 即将图像中的局部特征量化为视觉词并建立直方图检索图像。然而, 由于量化后的视觉词缺少了特征间的空间关系, 降低了局部特征的辨别能力, 会产生错误的匹配结果并影响检索性能。因此, 目前很多研究在得到匹配特征后, 通过几何约束的方式在后验证步骤中过滤错误的匹配特征对。这些方法通常计算整幅图像中的所有匹配特征对是否满足一致的几何变换关系, 并且可以分为全匹配和弱匹配两种方式。

全匹配方法通常基于Ransac算法^[4]计算查询图像与候选图像的仿射变换, 这种方式可以有效地验证匹配特征的几何一致性, 但耗时太长, 只适用于验证少量图像。弱匹配方法可以在不显示计算仿射变换矩阵的情况下验证匹配特征的几何一致性, Jegou等^[5]提出了Weak geometric consistency(WGC)方法, 假设在不同的尺度和旋转角度变换下, 会出现明显的峰值, 以此过滤错误的匹配特征。Tsai等^[6]提出了Location geometric similarity scoring(LGSS)方法使用任意两点特征的欧式距离比, 验证几何一致性, 有效地提高了运算效率。进而, Zhao等^[7]提出了Triangle spatial pattern(TSP)方法, 利用更多的点探索匹配特征间的几何关系, 通过验证相似三角形的数量来度量几何一致性。Zhou等^[8]提出了新的几何编码方法(GC), 通过轴线编码和方形编码严格地描述了局部特征间的几何关系。

无论是全匹配还是弱匹配, 都是计算整幅图像中所有匹配特征间的空间关系; 然而在后验证步骤中, 有些不相关匹配特征的计算对于改善检索性能的作用不大。不论相似区域是部分图像还是整幅图像, 均要满足相似的局部区域中所有正确匹配形变相似的特点。因此只需要验证局部区域内的匹配特征是否满足一致的几何关系即可, 没有必要计算局部区域外的不相关匹配特征。

针对上述现象, Xie等^[9]提出了Local geometric consistency(LGC)方法, 假设图像发生形变时, 基于局部区域特征相似的特点, 考虑了匹配特征相邻区域特征点的信息, 精确计算了匹配特征间的变换矩阵。然而, 对于一对匹配特征, LGC方法只是计算了最邻近的10对匹配特征的相关信息。如果局部区域内并不存在匹配特征, 这种方法很难描述局部区域内特征间的空间关系, 因此不相关特征仍然参与到在后验证步骤中。

本文通过局部邻域内匹配特征对的数量, 定义局部邻域约束值, 以此判断是否满足局部邻域的约束条件。若满足约束条件, 则计算局部邻域内的所有相关匹配特征是否满足一致的几何变换, 并以此建立后验证准则, 并对检索结果重新排序。

1 基于局部约束的后验证方法

1.1 局部邻域约束

图1为局部邻域约束的处理流程, 其中(a)表示查询图像与候选图像的9个匹配特征对。(b)中红色圆表示匹配对(q₁, d₁_')基于特征的尺度参数得到的局部邻域。(c)表示局部邻域内共同匹配特征作用于中心匹配对(q₁, d₁_')的约束关系, 粗实线双箭头所指的特征点位于中心匹配对的局部邻域内, 被视为相关匹配的特征, 线虚细双箭头指的特征则表示不相关的匹配特征。

	Figure Option View Download New Window
	图1 局部邻域的约束示例流程图Fig.1 The flow example of local constraint method

在查询图像I_q与候选图像I_d中, Q=(q₁, q₂, …, q_K), D=(d₁_', d₂_', …, d_K')分别表示特征集合。以此为基础, 进行SIFT特征的匹配, 进而得到两幅图像的匹配特征集M(Q, D)= $\begin{matrix} \{(q_{i}, d_{i'}) |q_{i} \in Q, d_{i'} \in D\} \end{matrix}$ , 其中q_i, d_i'分别表示查询图像与候选图像的特征。该特征描述包含4种信息:128维的SIFT描述符des, 尺度参数scl, 梯度方向参数θ 与特征在图像中的坐标(x, y)。

首先, 选择一个匹配对(q_i(x_i, y_i, des_i, scl_i, θ _i), d_i'(x_i', y_i', des_i', scl_i', θ _i'))作为测试中心匹配对, 验证其是否为正确匹配对。然后, 选取测试中心匹配特征的局部邻域, 其范围定义如下:

$\begin{matrix} \begin{matrix} D_{q_{i}} = σ_{constant} * sc l_{i} (1) \\ D_{d_{i'}} = σ_{constant} * sc l_{i'} (2) \end{matrix} \end{matrix}$

式中:scl_i与scl_i'分别表示q_i与d_i'中尺度参数。σ _constant是控制局部邻域大小的参数, 在实验2.3部分进行分析。

其次, 筛选局部邻域中的共同匹配特征, 并对测试中心匹配特征约束。共同匹配特征定义如下:

$\begin{matrix} ComMatc h_{(q_{i}, d_{i'})} = \{(q_{j}, d_{j'}) |\begin{matrix} (q_{j}, d_{j'}) \in M (Q, D) \\ dist (q_{i}, q_{j}) < D_{q_{i}} \\ dist (d_{i'}, d_{j'}) < D_{d_{i'}} \end{matrix}\} (3) \end{matrix}$

其中dist(· , · )指一对特征描述符的欧氏距离。最后计算该匹配对的局部邻域约束值。

$\begin{matrix} Constraint (q_{i}, d_{i'}) = C_{ComMatc h_{(q_{i}, d_{i'})}} - \frac{C_{M (Q, D)}}{C_{ComMatc h_{(q_{i}, d_{i'})}}} (4) \end{matrix}$

式中:C_M₍_Q_,_D₎是查询图像与候选图像匹配特征对的数量, 在图1示例中, C_M₍_Q_,_D₎=9。 $\begin{matrix} C_{ComMatc h_{(q_{i}, d_{i'})}} \end{matrix}$ 指测试中心匹配对(q_i, d_i')中, 局部邻域内共同匹配特征的个数, 图1示例中, $\begin{matrix} C_{ComMatc h_{(q_{1}, d_{1'})}} \end{matrix}$ =3。当约束值大于某一阈值δ ₁时, 计算其局部邻域内的共同匹配对是否满足一致的几何关系; 否则, 判断为错误匹配对。本文阈值定义为δ ₁=0.15× C_M₍_Q_,_D₎。通过大量实验证明, 阈值δ ₁决定局部邻域的范围, 阈值过大导致不相关匹配特征的计算, 阈值过小会丢失部分相关匹配特征的计算, 均影响检索性能。

1.2 空间验证

本文通过测试中心匹配对的局部邻域内共同匹配特征在横向与纵向中的排列顺序是否一致, 验证该测试匹配特征是否正确。

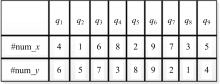
首先, 建立查询图像与候选图像间匹配特征点的排序列表。该列表是根据查询图像与候选图像匹配特征点的位置信息, 并以横向与纵向两种方式将特征点的坐标升序排列, 生成特征点的横向排列序号#num_x与纵向排列序号#num_y。图2给出查询图像中匹配特征点的排序列表的实例。

	Figure Option View Download New Window
	图2 查询图像中匹配特征点的排序列表Fig.2 The ranking list of matched features of query image

然后, 根据以上得到的测试中心匹配对的局部邻域内共同匹配特征与匹配特征点在排序列表中的特征排列序号, 计算测试中心匹配中, 局部邻域内共同匹配特征间的位置关系, 计算如下:

$\begin{matrix} \begin{matrix} D_x (q_{i}, q_{m}, q_{n}) = # num_x (q_{n}) - # num_x (q_{m}) (5) \\ D_y (q_{i}, q_{m}, q_{n}) = # num_y (q_{n}) - # num_y (q_{m}) (6) \end{matrix} \end{matrix}$

其中, (q_m, d_m')∈ ComMatc $\begin{matrix} h_{(q_{i}, d_{i'})} \end{matrix}$ ; (q_n, d_n')∈ ComMatc $\begin{matrix} h_{(q_{i}, d_{i'})} \end{matrix}$ , 并且n> m。D_x(q_i, q_m, q_n), D_y(q_i, q_m, q_n)分别表示在测试中心匹配对(q_i, d_i')的局部邻域内共同匹配对中, 特征q_n与特征q_m间的横向坐标关系与纵向坐标关系。当D_x(q_i, q_m, q_n)大于0时, 表示中心匹配对(q_i, d_i')的局部邻域内共同匹配对中特征q_n在特征q_m的右边; 当D_y(q_i, q_m, q_n)大于0时, 表示中心匹配对(q_i, d_i')中局部邻域内共同匹配对中特征q_n在特征q_m的上边; 当D_x(q_i, q_m, q_n)和D_y(q_i, q_m, q_n)都小于0时, 反之。

进一步, 根据得到的查询图像与候选图像中测试中心匹配对的局部邻域内共同匹配对间的横向坐标关系与纵向坐标关系, 对其验证是否一致, 验证定义式如下:

$\begin{matrix} \begin{matrix} Verify_x ((q_{i}, d_{i'}), (q_{m}, d_{m'}), (q_{n}, d_{n'})) = \\ \{\begin{matrix} 1, & cond 1 \\ 0, & cond 2 \end{matrix} (7) \\ Verify_y ((q_{i}, d_{i'}), (q_{m}, d_{m'}), (q_{n}, d_{n'})) = \\ \{\begin{matrix} 1, \begin{matrix} cond 3 \end{matrix} \\ 0, \begin{matrix} cond 4 \end{matrix} \end{matrix} (8) \end{matrix} \end{matrix}$

当查询图像中D_x(q_i, q_m, q_n)与候选图像中D_x(d_i', d_m', d_n')同时大于0, 或者D_x(q_i, q_m, q_n), D_x(d_i', d_m', d_n')同时小于0时, 该匹配特征对(q_m, d_m'), (q_n, d_n'), 在横向坐标关系中, 验证正确, Verify_x((q_i, d_i'), (q_m, d_m'), (q_n, d_n'))=1, 即cond1; 若D_x(q_i, q_m, q_n)大于0, D_x(d_i', d_m', d_n')小于0, 或者D_x(q_i, q_m, q_n)小于0, D_x(d_i', d_m', d_n')大于0时, 验证错误, Verify_x((q_i, d_i'), (q_m, d_m'), (q_n, d_n'))=0, 即cond2。

同理, 当D_y(q_i, q_m, q_n), D_y(d_i', d_m', d_n')同时大于0, 或者同时小于0时, 匹配特征对在纵向坐标关系中, 验证正确, Verify_y((q_i, d_i'), (q_m, d_m'), (q_n, d_n'))=1, 即cond3; 反之, 验证错误, Verify_y((q_i, d_i'), (q_m, d_m'), (q_n, d_n'))=0, 即cond4。

从而, 根据局部邻域中匹配特征在横向与纵向的验证信息, 计算该测试中心匹配特征在局部邻域内的几何得分, 如下:

$\begin{matrix} \begin{matrix} Score (q_{i}, d_{i'}) = \\ \max [\sum_{\begin{matrix} (q_{m}, d_{m'}) \in ComMatc h_{(q_{i}, d_{i'})} \\ (q_{n}, d_{n'}) \in ComMat c h_{(q_{i}, d_{i'})} \\ m \to n \end{matrix}} \\ Verify_x ((q_{i}, d_{i'}), (q_{m}, d_{m'}), (q_{n}, d_{n'})), \\ \sum_{\begin{matrix} (q_{m}, d_{m'}) \in ComMatc h_{(q_{i}, d_{i'})}, \\ (q_{n}, d_{n'}) \in ComMatc h_{(q_{i}, d_{i'})} \\ m \to n \end{matrix}} \\ Verify_y ((q_{i}, d_{i'}), (q_{m}, d_{m'}), (q_{n}, d_{n'}))] \end{matrix} \end{matrix}$

其中, m→ n表示局部邻域匹配特征中, id号为n的特征与id号为m的特征之间的约束关系。为了提高计算效率, 本文并非验证共同匹配对中所有特征点间的约束关系, 只是计算了共同匹配特征点的排序列表中相邻特征id号间的约束关系。因此该约束关系可表示为, 特征id号为n是大于特征id号为m的最小id号。如图1所示, 当测试中心匹配对为(q₁, d₁_'), m=3时, 在查询图像的局部邻域内共同匹配特征{q₃, q₅, q₉}中, 大于特征q₃的id号3的最小id号为特征q₅id号5, 因此n=5。几何得分Score(q_i, d_i')表示中心匹配对(q_i, d_i')的局部邻域内所有共同匹配特征点在横向坐标关系与纵向坐标关系中, 排列顺序一致的最多数量。

假设如果该得分大于阈值δ ₂, 判断测试匹配对(q_i, d_i')正确; 反之, 错误。本文定义阈值δ ₂=0.3× $\begin{matrix} C_{ComMatc h_{(q_{i}, d_{i'})}} \end{matrix}$ 。最后, 根据正确匹配对的个数对初始检索结果重新排序。

2 实验结果及讨论

本文通过检索精确度与检索时间验证SVLRC的检索性能。并与目前几种普遍的几何验证方法^{[4, 5, 6, 7, 8, 9]}作比较。实验中计算初始检索后的前1000幅图像的几何得分, 并重排序。在CPU为Core i5, 3.30 GHz, 8 GRAM, 64位的WIN7操作系统, Matlab R2012a中进行测试。

2.1 实验图像集

实验数据为两组数据集:第一组为DupImage数据集^[10], 包含1104幅图像, 并分为33组。本文随机选择100幅作为测试图像, 并以mAP^[11]作为检索精度的度量方式。第二组为Mobile数据集^[12], 包含400幅图像。同时也提供了手机拍摄的2500幅测试图像集。以Top-10作为衡量精确度的标准。每组测试集从图像库Ukbenchc中选取一定数量的图像作为混淆图像, 最终两组数据集的图像总数均为10 000幅。

2.2 实验准备

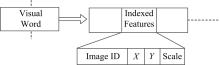
本文是在传统的BoW检索模型的基础上提取SIFT特征。同时记录特征点的位置信息, 尺度作为几何验证的计算条件。提取特征前, 将大尺寸图像降采样为小于500* 500。并采用分级树形的方法^[11]生成1 M个视觉词。使用倒排文件方式索引图像, 如图3所示, 每个视觉词都与多个索引特征相链, 其中每个索引特征包含图像的ID、特征位置、尺度参数。实验中所有几何验证方法都是对基于BoW得到初始检索结果的前1000幅图像进行验证重排序的。

	Figure Option View Download New Window
	图3 倒排文件结构Fig.3 Inverted file

2.3 参数测试

在本文SVLRC的方法中, 参数σ _constant是通过控制局部邻域的大小范围确定相关匹配特征的个数, 并影响检索性能。本文测试不同的σ _constant值所对应的检索性能, 并确定最优的σ _constant。

不同σ _constant值对第一组数据集DupImage检索性能的影响见图4, 同时给出了不同σ _constant值所对应的在后验证阶段中的计算时间。

从图4可知σ _constant值越大, 中心匹配特征对的局部邻域范围越大, 在过滤不相关匹配特征的前提下, 可以得到更多相关匹配特征, 并提高检索的精确度。然而, 过大的σ _constant值, 也可能导致一些不相关的匹配特征参与在后验证阶段中, 最终影响检索性能。对于时间消耗, σ _constant值越大, 在后验证阶段计算匹配特征的数量越多, 并导致消耗更多的计算时间。基于上述的考虑, 对于SVLRC方法, 当σ _constant=40时, mAP为0.8109, 计算时间为0.8697 s, 此时为参数σ _constant的最优选择, 并在下面的实验中均采用这个参数设定。

	Figure Option View Download New Window
	图4 不同σ _constant值的检索性能Fig.4 The retrieval performance of different

2.4 与其他几何验证算法的性能对比

本文分析了SVLRC方法对检索性能的影响, 并与其他7种几何验证方法(BoW^[3], LGSS^[6], WGC^[5], LGC^[9], TSP^[7], RANSAC^[4], GC^[8])的检索精确度和计算时间进行了比较, 如表1所示。若所比较算法的程序中含有参数, 则采用它们的默认值, 并且在第一组DupImage数据集中, 以mAP作为精确度的衡量标准, 在第二组Mobile数据集中, 以Top-10作为精确度的衡量标准。由于RANSAC耗时较大, 因此只对初始检索结果的前300幅图像进行验证重排序。

表1 两种数据集中, 各种检索方法的精确度和查询时间 Table 1 The accuracy and query time of each retrieval methods in the two data sets

通过表1中检索精确度的值可以明显看出, 传统的BoW算法忽略了特征间的几何关系而使检索效率较低。而本文所提出的基于局部邻域约束的空间验证方法, 重点强调特征描述子之间的几何关系, 从而进一步提高了检索性能。关于其他几何验证方法, LGSS两点编码时, 验证特征匹配很不稳定; WGC主要假设查询图像与候选图像的变换一致, 却无法处理图像间的非刚性形变; RANSAC与TSP都是只编码了特征点的位置信息, 无法全面反应匹配特征间的空间关系; 虽然GC完全利用特征的几何信息(尺度、方向、空间位置), 但不相关特征在后验证中的计算也对检索性能产生了影响; 对于LGC, 在几何编码中只是计算了最邻近的10对匹配特征的相关信息, 如果局部区域内并不存在匹配特征, 此时不相关特征仍然会计算在后验证步骤中; 以上叙述的原因都会影响检索性能。

对表1关于每幅图像的平均查询时间的分析, 在众多几何验证方法的对比中可看出, 相比WGC(0.3237 s), LGSS(0.4008 s)计算的是两点的距离比, 而不是简单的加减运算; LGC(0.5261 s)又额外考虑了最邻近的10对匹配特征的信息, 精确计算了匹配特征间的变换矩阵; GC(2.4377 s)提出了更加复杂的编码方法(轴线编码和方形编码), 严格地描述了局部特征间的几何关系; TSP(7.7272 s)通过更多的点计算特征间的几何关系; 由于RANSAC(15.1747 s)通过大量的随机取样, 计算仿射变换, 因此耗时最多。最后, SVLRC在验证特征间几何关系的前提下, 通过定义匹配特征中局部邻域的约束方法, 过滤不相关的匹配特征对, 不仅减少了后验证阶段特征的计算数量, 也提高了验证错误匹配特征的准确度。

2.5 检索实例

图5显示了SVLRC和其他方法的检索结果, 图5中, 箭头左边为查询图像, 箭头右边为前5幅检索图像。这些结果对于检索目标的颜色、尺度、方向的变化证明了本文方法在图像复杂变换中的有效性。

	Figure Option View Download New Window
	图5 不同方法的检索结果Fig.5 Comparison of performance for different methods

3 结论

在复杂背景的目标检索的研究中, 由于传统检索模型(BoW)忽略了特征间的几何关系, 导致检索效率降低。而且, 目前大多数几何验证方法都是计算整幅图像中所有匹配特征间的空间关系, 然而, 在后验证步骤中, 不相关匹配特征的计算对于改善检索性能的作用不大。因此, 本文提出基于局部邻域约束的空间验证方法, 通过定义匹配特征的局部邻域范围, 过滤不相关的匹配特征对, 最后计算相关匹配特征是否满足一致的几何变换。实验中, 利用DupImage和Mobile数据集, 与其他常用的几何验证方法作比较, 结果表明, 本文提出的方法可以在保证检索速度的前提下, 提高检索的精确度。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Zheng L, Wang S, Zhou W, et al. Bayes merging of multiple vocabularies for scalable image retrieva[C]∥IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, 2014: 1963-1970. [本文引用:1]
[2]	赵宏伟, 李清亮, 刘萍萍. 基于分级显著信息的空间编码方法[J]. 电子学报, 2014, 42(9): 1863-1867. Zhao Hong-wei, Li Qing-liang, Liu Ping-ping. Spatial encoding based on hierarchical salient information[J]. Acta Electronica Sinica, 2014, 42(9): 1863-1867. [本文引用:1]
[3]	Sivic J, Zisserman A. Video Google: A text retrieval approach to object matching in videos[C]∥Proceedings of 9th IEEE International Conference on Computer Vision, Nice, France, 2003: 1470-1477. [本文引用:2]
[4]	Fischler M A, Bolles R C. Rand om sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography[J]. Communications of the ACM, 1981, 24(6): 381-395. [本文引用:3]
[5]	Jegou H, Douze M, Schmid C. Hamming embedding and weak geometric consistency for large scale image search[C]∥Proceedings of the 2008 10th IEEE European Conference on Computer Vision. Marseille, France: IEEE, 2008: 304-317. [本文引用:3]
[6]	Tsai S S, Chen D, Takacs G, et al. Fast geometric re-ranking for image-based retrieval[C]∥Proceedings of the 2010 IEEE International Conference on Image Processing. Hong Kong: IEEE, 2010: 1029-1032. [本文引用:3]
[7]	Zhao H, Li Q, Liu P. Hierarchical geometry verification via maximum entropy saliency in image retrieval[J]. Entropy, 2014, 16(7): 3848-3865. [本文引用:3]
[8]	Zhou W, Li H, Lu Y, et al. Sift match verification by geometric coding for large-scale partial-duplicate web image search[J]. ACM Transactions on Multimedia Computing, Communications, and Applications (TOMCCAP), 2013, 9(1): 1-18. [本文引用:3]
[9]	Xie H, Gao K, Zhang Y, et al. Local geometric consistency constraint for image retrieval[C]∥Proceedings of the 2011 18th IEEE International Conference on Image Processing. Brussels, Belgium: IEEE, 2011: 101-104. [本文引用:3]
[10]	https://dl.dropboxusercontent.com/u/42311725/DupGroundTruthDataset.rar[DB/OL], 2014-07-10 [本文引用:1]
[11]	Philbin J, Chum O, Isard M, et al. Object retrieval with large vocabularies and fast spatial matching[C]∥IEEE Conference on Computer Vision and Pattern Recognition, Barcelona, Spain, 2007: 1-8. [本文引用:2]
[12]	Wang X, Yang M, Cour T, et al. Contextual weighting for vocabulary tree based image retrieval[C]∥Proceedings of the 2011 IEEE International Conference on Computer Vision, Barcelona, Spain, 2011: 209-216. [本文引用:1]

2014

0.0

... 0 引言随着多媒体信息的迅速发展,图像检索技术已成为研究热点^[1,2],然而大多数图像检索系统都是基于Bag of Words(BoW)模型^[3]实现,即将图像中的局部特征量化为视觉词并建立直方图检索图像 ...

2014

0.0

. 2014, 42(9):1863-1867 DOI:10.3969/j.issn.0372-2112.2014.09.031

Spatial encoding based on hierarchical salient information

基于分级显著信息的空间编码方法

Zhao Hong-wei , Li Qing-liang , Liu Ping-ping.

赵宏伟, 李清亮, 刘萍萍

1. School of Computer Science and Technology, Jilin University, Changchun, Jilin 130012, China; 2. Key Laboratory of Symbolic Computation and Knowledge Engineering of Ministry of Education, Changchun, Jilin 130012, China

The traditional model "Bag of Words" does not capture the spatial relationship among local features,thus affecting the retrieval performance.Hence,the spatial encoding method based on hierarchical salient information is proposed,which aims at fully exploring the geometric context of all visual words in images and increasing the discriminative power of the features based on hierarchical salient information.We propose a new encoding method in the geometric verification step.The spatial layout of every 3 points within a certain salient area will be represented by angle encoding and location encoding,meanwhile we sum all spatial matching scores with weights based on hierarchical salient information to generate the final ranking list.Experimental results prove that our scheme improves the retrieval accuracy significantly and reduces the computing time during the geometric verification step.

传统的Bag of Words模型检索方法并不具备局部特征间的空间关系，因此影响检索性能.本文提出了基于分级显著信息的空间编码方法.通过分层次的提取显著区域并对每个显著区域内的特征点进行空间编码.目的是探索特征间的空间关系，并根据分级显著信息提高特征间的相关性.在几何验证过程中，本文通过任意三点间的角度编码和位移编码构成的空间编码方法完成图像对之间的空间关系匹配，同时根据图像各个区域间的显著程度赋予该区域空间关系匹配得分相应权重，得到最终的几何得分，重新排列检索结果.实验结果表明本文提出的方法既改善了最终检索结果的精确度又降低了几何验证阶段的计算时间.

2003

0.0

... 4 与其他几何验证算法的性能对比本文分析了SVLRC方法对检索性能的影响,并与其他7种几何验证方法(BoW^[3],LGSS^[6],WGC^[5],LGC^[9],TSP^[7],RANSAC^[4],GC^[8])的检索精确度和计算时间进行了比较,如表1所示 ...

1981

0.0

... 全匹配方法通常基于Ransac算法^[4]计算查询图像与候选图像的仿射变换,这种方式可以有效地验证匹配特征的几何一致性,但耗时太长,只适用于验证少量图像 ...