作者简介:王军年(1981-),男,副教授,博士.研究方向:电动汽车节能控制技术,电动汽车系统动力学.E-mail:wjn@jlu.edu.cn
介绍了一种新型双电机构型纯电动汽车,并分析了其结构特征和工作模式,针对新构型的动力系统进行参数匹配和控制策略研究。在MATLAB/Simulink中建立离线仿真模型验证匹配参数合理性和控制策略可行性。仿真结果表明:与传统单电机构型相比,新型双电机构型纯电动汽车的节能潜力达到10%左右。
A novel pure electric vehicle with dual motors configuration is introduced. The energy conservation potential and mechanism of this new vehicle are analyzed. First, the structural characteristics and operating mode are investigated. Then the parameters of the powertrain and control strategy are designed. The rationality of the parameters and the validity of the control strategy are demonstrated in MATYLAB/Simulink. As compared to the traditional pure electric vehicle, the energy conservation potential of the new pure electric vehicle with dual motors is around 10%.
作为最有潜力的新能源汽车, 纯电动汽车具有零排放、噪音低、零油耗的优点。然而当前技术条件下, 纯电动汽车依然面临续驶里程短、整车价格昂贵的发展瓶颈。提高电动汽车的经济性对于降低续驶里程和整车价格的约束具有重要意义。文献[1]提出的双电机构型纯电动汽车极大地提高了纯电动汽车的经济性。英国的Vocis公司和北京新能源汽车股份有限公司等[2, 3]针对双电机纯电动汽车的构型结构进行了探究。
本文设计的双电机构型纯电动汽车是在已有的某款具有单电机驱动的纯电动汽车上进行的驱动方案改进, 其目的是在保证实现原车动力性指标的前提下提升此纯电动汽车的经济性, 为此提出了一种新型的双电机耦合装置。该双电机构型纯电动汽车能够同时实现转矩耦合驱动和转速耦合驱动两种模式, 具有可观的节能潜力。通过改变车辆构型来提高纯电动车的经济性成为一种可行的技术途径。
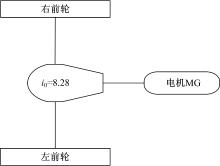
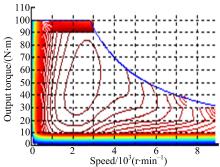
原车采用单电机带驱动桥结构, 主减速器传动比为8.28, 原车单电机构型如图1所示。原车的电机MG参数如下:峰值功率为90 kW; 额定功率为45 kW; 最大转矩为210 N· m; 额定转矩为120 N· m; 最高转速为9000 r· min-1; 额定转速为3500 r· min-1。原车电机MG的MAP图如图2所示。
图3为本文研究的双电机构型纯电动汽车动力系统的结构示意图。
电机MG2通过离合器C2直接与行星排的太阳轮连接; 电机MG1通过减速结构与行星排的活动齿圈连接。离合器C1和制动器B1分别控制行星排的活动齿圈和固定齿圈的闭合状态; 离合器C2控制电机MG1与主驱动轴的连接状态。动力经行星架输出, 与车辆的主减速器连接。
表1为构型的工作状态列表, 通过控制离合器C1、C2、C3和制动器B1的闭合状态, 本构型能够实现以下4种工作模式:电机MG1单独驱动; 电机MG2单独驱动; 双电机转矩耦合驱动; 双电机转速耦合驱动。
| 表1 模式切换状态 Table 1 Mode switching status |
转矩耦合驱动时构型运动学关系如下:
式中:nMG1、TMG1分别为MG1的转速、转矩; nMG2、TMG2分别为MG2的转速、转矩; nC、TC分别为行星架转速、转矩; k表示行星排特征参数。
转速耦合驱动时构型运动学关系如下:
式中:i为电机MG1和活动齿圈的传动比。
由式(2)可知转矩耦合驱动模式下整车的输出转矩为两个电机的输出转矩之和, 因此该模式适用于低速大扭矩工况; 同样由式(3)可知转速耦合模式下整车的车速可以通过两个电机的转速加以调节, 因此该模式适用于低扭矩高转速工况。
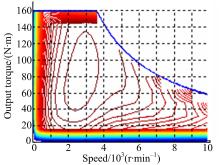
动力系统参数匹配首先依据车辆动力学指标进行整车参数匹配, 然后通过对常用工况进行数理统计, 对双电机功能进行划分, 进而确定双电机参数。目标车型参数及动力性指标如下:整备质量为1552 kg; 满载质量为1928 kg; 迎风面积为2.56 m2; 空气阻力系数为0.3; 滚阻系数为0.01; 轮胎半径为307 mm; 轴距为2675 mm; 最高车速为147 km/h; 百公里加速时间为14.7 s; 最大爬坡度为28%(20 km/h)。匹配出的电机MG1和MG2的MAP图如图4和图5所示。
整车峰值功率应该满足最高车速、最大爬坡度和百公里加速时间的要求[4], 因此峰值功率应该取三者之中的最大值。
式中:Pmax_1、Pmax_2、Pmax_3分别表示按照最高车速、最大爬坡度和百公里加速时间计算的峰值功率。
整车最大转矩一般满足最大爬坡度和起步加速度的设计要求, 因此取两个最大转矩的较大值。
式中:Tmax_1、Tmax_2分别表示按照最大爬坡度和起步加速度设计要求计算的最大转矩。其中计算起步加速度设计要求时, 只要满足最大起步加速度范围为2~2.5 m/s2, 就可以满足绝大多数工况下的起步加速度需求[5]。
整车最大传动比需要满足的条件:车轮获得的最大驱动力应该满足最大爬坡度的要求[6]。
电机最大转矩对应的车轮驱动力:
滑移状况下爬坡时获得的最大车轮驱动力:
则车轮最终获得的车轮驱动力:
考虑驱动力与爬坡时的阻力关系:
当车速为20 km/h时, 车辆传动系总传动比i对应的车轮获得的驱动力、车辆爬坡时受到的阻力和动力电机能提供的最大驱动转矩3个变量的变化趋势如图6所示。
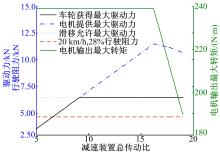 | 图6 不同传动比对应电机输出转矩、最大驱动力和行驶阻力Fig.6 Output torque, maximum driving force and resistance of different transmission ratio |
车辆的驱动力应该能够满足最大爬坡度的要求, 则车辆的驱动力需要大于车辆受到的爬坡阻力。即图6中黑色的最大驱动力的坐标需要大于红色的行驶时爬坡阻力的坐标。这样可以得到整车传动系总传动比的变化范围为:
双电机的功能划分主要是结合工作模式和整车电机性能参数, 确定电机MG1和电机MG2的性能参数。在整车参数匹配的基础上, 两个电机的参数匹配应该满足如下条件:①两个电机的联合工作区域应不小于前面匹配的整车电机工作区域; ②对两个电机合理进行功率划分, 使双电机单独工作区域与耦合工作区域合理分布; ③尽量提高两个电机的高效率区间利用率。两个电机高效率区间的利用率与电机的频繁工作区域密切相关。而频繁工作区与车辆的行驶工况息息相关, 因此有必要对常用试验循环工况的电机工作点和车速频次进行数理统计分析, 最终得到电机工作频次较高区域, 据此对双电机的功能进行划分。
如表2所示, 本文通过对常用测试工况进行数理统计, 得到电机工作的高频车速区间为0~20 km/h和35~55 km/h。这样可以对两个电机进行功能划分, MG2为主电机, 满足整车稳态功率需求。MG1为辅助电机, 满足整车瞬态功率需求。同时两个电机的高效率区尽可能覆盖统计的高频车速区间。
| 表2 常用工况数理统计数据 Table 2 Mathematical statistics for driving cycles |
转速耦合模式下, 为了满足最高车速要求, 两个电机的转速需要满足下式:
转速耦合模式下, 两个电机的转矩关系满足:
一般情况下主电机的转速和转矩均大于辅助电机。由式(12)(13)可知, 为了满足电机MG1的转速小于MG2, 需要k/i> 1; 为了满足电机MG1的转矩小于MG2, 需要k/i< 1。所以k/i的比值大约等于1。
最终动力系统的参数匹配结果如表3所示。
| 表3 动力系统参数 Table 3 Parameters for powertrain |
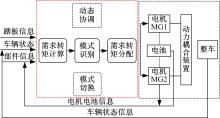
本文构型采用的控制策略软件架构如图7所示, 控制策略主要分为需求转矩计算、模式识别和需求转矩分配三部分。
基准转矩满足车辆的基本转矩需求, 计算公式如下所示。
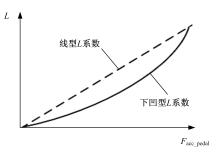
式中:Tmax、Tmax_MG1、Tmax_MG2分别表示当前车速下整车能提供的最大转矩、电机MG1能提供的最大转矩、电机MG2能提供的最大转矩; L表示加速踏板对转矩的符合系数, 原车采用动力模式加经济模式, 动力模式偏重于驾驶员的操纵体验, 经济模式下采用侧重经济性的“ 下凹型曲线” 。在相同踏板开度(Facc_pedal)下, “ 上凸型” 基准转矩MAP形成的基准转矩大于“ 下凹型” 基准转矩MAP形成的基准转矩。这样车辆的消耗功率势必增加。新构型侧重于整车经济性, 故本文采用侧重经济性的“ 下凹型” L系数, 如图8所示[7]。
由于本文所匹配的双电机构型电动汽车侧重于经济性, 当车辆在急加速工况时会出现动力不足的情况, 故需要施加补偿转矩。补偿转矩主要为了弥补车辆急加速工况下的转矩需求, 如图9所示。本文根据加速踏板开度及加速踏板开度变化率, 将加速工况分为平缓加速、一般加速和急加速三种工况[8], 分别设定不同踏板开度和变化率阈值, 基于这两个参数分别对应相应的补偿转矩修正系数λ 1、λ 2、λ 3。则补偿转矩的计算公式如下所示:
本文采用基于瞬时优化的模式识别策略[9], 具体如图10所示。
当油门踏板给出一个需求转矩时, 通过对比电机MG1单独工作时的电功率、电机MG2单独工作时的电功率、电机MG1和MG2按照转矩耦合模式工作时的电功率、电机MG1和电机MG2按照转速耦合模式工作时的电功率, 取电功率最小所对应的模式作为当前的工作模式。即实时计算当前状态下本构型的4种工作模式下每种模式的需求功率, 最终选取需求功率最小的那种模式作为当前状态下的工作模式。对于混合动力汽车, 基于瞬时优化的控制策略的关键在于如何确定油电转化系数。而对于双电机构型纯电动车而言, 并不存在这个问题。基于瞬态优化的模式识别策略的核心, 就是找出当前需求转矩下的最优工作点, 最优工作点满足消耗电功率最小。找到对应的最优工作模式后, 则可获得每种工作模式下相应的转矩分配策略。
通过在MATLAB/Simulink中建立离线仿真模型, 可以对比分析双电机构型与单电机构型的能耗情况。
图11、图12分别是NEDC工况、UDDS工况下电机工作点分布图。结合前文中的电机MG的MAP图2, 电机MG1和电机MG2的MAP图4和图5, 由图11可以看出, NEDC工况下双电机构型的电机工作点的负荷率明显高于单电机构型, 这样双电机构型的平均工作效率将高于单电机构型。同样, 结合前文的图2、图4和图5, 由图12可以看出, UDDS工况下两种构型的电机工作点分布呈现同样的规律, 即双电机构型分布点更好, 效率更高。
表4为5种常用循环测试工况下, 双电机构型相对于单电机构型的百公里能耗仿真数据。结果显示UDDS工况下双电机构型节能潜力最大, 达到12.63%, JC08工况下双电机构型节能潜力相对较小, 但也达到8.95%, 平均来看双电机构型相对于单电机构型的节能潜力达到10%左右。
| 表4 循环工况能耗统计 Table 4 Energy consumption statistics in driving cycles |
本文提出一种能实现转矩和转速耦合的双电机构型纯电动汽车动力系统新构型, 在模式分析的基础上完成了参数匹配和控制策略研究, 并通过仿真验证了该构型的节能潜力。结果显示, 双电机构型相对于传统单电机构型的节能潜力达到10%左右。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|