基于信道估计的OFDM定时同步算法

引用本文

许炜阳, 周杰, 王雨晴, 吴玉成. 基于信道估计的OFDM定时同步算法. 吉林大学学报: 工学版, 2016, 46(1): 290-295
XU Wei-yang, ZHOU Jie, WANG Yu-qing, WU Yu-cheng. OFDM timing synchronization algorithm based on channel estimation. Journal of Jilin University Engineering and Technology Edition, 2016, 46(1): 290-295 复制到剪切板

Permissions

基于信道估计的OFDM定时同步算法

许炜阳, 周杰, 王雨晴, 吴玉成

重庆大学通信工程学院,重庆 400044

作者简介:许炜阳(1982-),男,副教授,博士.研究方向:下一代移动通信系统.E-mail:weiyangxu@cqu.edu.cn

基金:国家自然科学基金项目(61201177); 重庆市自然科学基金重点项目(cstc2013jjB40004)

摘要

针对正交频分复用(OFDM)系统在多径衰落信道第一径不是最强径时存在定时错误,以及现有精同步算法漏检概率大的问题,提出利用信道冲激响应循环右移特性实现对第一径的精确检测。该算法先通过粗同步定位到能量最强径,再使用最小二乘(Least square)算法求出信道冲激响应,根据滑动窗口内能量变化判断各径所在位置,最后采用自适应门限法检测出第一径。理论分析和仿真结果表明:本文算法同已有算法相比,可降低精确符号同步的漏检概率,有效提高系统的定时性能。

关键词: 通信技术; 正交频分复用; 定时同步; 第一径延时; 最小二乘算法

中图分类号:TN929.5 文献标志码:A 文章编号:1671-5497(2016)01-0290-06

OFDM timing synchronization algorithm based on channel estimation

XU Wei-yang, ZHOU Jie, WANG Yu-qing, WU Yu-cheng

College of Communication Engineering,Chongqing University,Chongqing 400044,China

Abstract

The timing errors in Orthogonal Frequency Division Multiplexing (OFDM), which occur when the first path is not the strongest one in the multipath fading channel, would incur a high probability of miss detection. To solve this problem, a timing synchronization algorithm was proposed, which can be used to exploit the cycle-right-shift property of channel impulse response to estimate precisely the first path delay. In this algorithm, first, the delay of the strongest path was estimated through coarse synchronization. Then, the channel impulse response was obtained using the Least Square (LS) algorithm, based on which the location of each path was determined according to the difference in a sliding window. Finally, the first path was detected using the adaptive threshold approach. Theoretical analysis and simulation results show that, compared with the existing methods, the proposed algorithm can decrease the probability of miss detection and improve the system timing performance.

Keyword: communication; orthogonal frequency division multiplexing (OFDM); timing synchronization; first arrival path delay; least square algorithm

Show Figures

0 引言

正交频分复用(OFDM)以其频谱利用率高、抗多径衰落能力强等特点在高速无线传输系统中得到广泛应用。文献[1-4]通过改进训练符号结构, 利用相关特性, 解决定时度量的峰值平台现象, 同时消除副峰值影响, 使定时更准确。这些粗同步算法均基于能量检测, 在多径衰落信道中, 同步在最强径上。若第一径不是最强径, 会使得DFT窗相对滞后, 引入符号间干扰。文献[5-9]在搜索到最强径的基础上, 通过精同步算法定位到第一径, 从而解决符号间干扰问题。文献[5]采用将已知的训练序列与接收信号相关, 通过设置判决参数来确定第一径, 但判决参数设置需反复验证。文献[6]利用判决门限将噪声和信号分离, 消除噪声影响, 再对相关范围内能量求和并搜索峰值, 但其存在峰值平台。文献[7]通过滑动窗口累加求和消除副峰值, 但要求窗口必须包含第一径, 同时避免含能量最强径, 故实现困难。文献[8]联合定时同步和信道估计, 在低信噪比时性能较好, 但因前导能量过大而不适用于低能量传输系统。文献[9]采用具有横幅零自相关特性的CAZAC序列, 消除副峰值, 且使阈值范围可调, 但当第一径衰落严重低于阈值时, 无法实现准确检测。

为提高OFDM系统在多径衰落信道中第一径检测精度, 本文提出一种基于信道估计的定时同步方法。该算法在粗同步定位到最强径的基础上, 依据最小二乘(LS)算法求得信道冲激响应, 再对其设置能量求和滑动窗口, 并采用基于窗口能量变化针对不同信道的自适应门限法, 实现对第一径的准确定位, 完成符号定时同步。

1 精确定时同步算法原理

本文的精确符号定时同步算法由粗同步和基于信道估计的精同步组成。

1.1 粗同步算法

通过Schmidl算法^[1]构造两段重复序列, 设C(2k)为频域偶数子载波上的PN序列, C(2k+1)=0, 其中0≤ k≤ A-1, A=N/2。则发送端的训练序列(不包含CP)可以表示为:

$\begin{matrix} c (n) = \frac{1}{\sqrt[]{N}} \overset{A - 1}{\sum_{k = 0}} C (2 k) e^{j 2 πkn / A}, 0 \leq n \leq N - 1 (1) \end{matrix}$

定义一个大小为N的滑动窗口, 定时度量函数M(d)^[10]为:

$\begin{matrix} \begin{matrix} M (d) = \frac{{|P (d)|}^{2}}{R^{2} (d)} (2) \\ 其中 : \\ P (d) = \overset{A - 1}{\sum_{i = 0}} [r (d + i) c (i)] * [r (d + i + A) c (i)] (3) \\ R (d) = \overset{A - 1}{\sum_{i = 0}} {|r (d + i + A)|}^{2} (4) \end{matrix} \end{matrix}$

式中:r(d)为收端数据; c(i)为发端从循环前缀开始的A个数据。由式(2)(3)(4)可知, 定时度量M(d)为从CP开始的本地数据与接收到的两段重复数据分别做相关运算后, 再进行延时相关处理的结果。

理想情况下, 定时度量最大值位置即为循环前缀开始的位置, 将其平移N_g(训练序列循环前缀的长度)点即得到粗同步定时点d_c, 在多径衰落信道下即为能量最大径的延时。为实现对第一径的精确定位, 需要进一步通过精同步算法将能量最大径修正回到第一径。

1.2 精同步算法

本文精同步算法首先依据LS算法求出信道的冲激响应, 因前导为两端重复结构, 故其具有循环右移特性。基于此特性, 可利用循环左移滑动窗口内能量变化判断各径所在位置, 最后通过最小值法或自适应门限法来找出第一径所在位置。

1.2.1 信道估计

设τ 为粗同步所估计定时位置d_c与理想定时位置d_s的差值, 则d_c=d_s+τ , 接收端从d_c开始的信号可以表示为:

$\begin{matrix} \begin{matrix} r (d_{c} + n) = e^{- jθ (n)} s (n + τ) + w (d_{c} + n) (5) \\ 0 \leq n \leq N - τ - 1 \end{matrix} \end{matrix}$

式中:s(n)= $\begin{matrix} \overset{v - 1}{\sum_{p = 0}} \end{matrix}$ h(p)c((n-p)modA), 其中v为信道的多径数目, 且v< N_g; h(p)为第p径信道的衰落系数, p为第p径的延迟样点数; θ (n)为由于频偏等原因产生的相偏; w(d_c+n)为零均值、方差为 $\begin{matrix} δ_{n}^{2} \end{matrix}$ 的复高斯白噪声。从d_c处取A点, 即式(5)中的n=0, 1, …, A-1, 得b(n), 经A点DFT变换得到:

$\begin{matrix} B (k) = \frac{1}{\sqrt[]{A}} \overset{A - 1}{\sum_{n = 0}} b (n) e^{- j 2 πkn / A} (6) \end{matrix}$

将式(5)带入式(6)中, 则

$\begin{matrix} \begin{matrix} B (k) = \frac{e^{- jθ (n)}}{\sqrt[]{A}} \times \\ \overset{A - 1}{\sum_{n = 0}} \overset{v - 1}{\sum_{p = 0}} \{h (p) c ((n + τ - p) modA) e^{- j 2 πkn / A}\} + \\ \frac{1}{\sqrt[]{A}} \overset{A - 1}{\sum_{n = 0}} w (d_{c} + n) e^{- j 2 πkn / A} (7) \end{matrix} \end{matrix}$

将式(1)带入式(7), 化简可得:

$\begin{matrix} B (k) = \sqrt[]{\frac{A}{2}} e^{- jθ (n)} C (2 k) H (k) e^{j 2 πkτ / A} + W (k) (8) \end{matrix}$

式中:H(k)=(1/ $\begin{matrix} \sqrt[]{A} \end{matrix}$ ) $\begin{matrix} \overset{v = 1}{\sum_{p = 0}} \end{matrix}$ h(p)e^-j^2π^pk/A; W(k)= $\begin{matrix} \frac{1}{\sqrt[]{A}} \end{matrix} \begin{matrix} \overset{A - 1}{\sum_{n = 0}} \end{matrix}$ w(d_c+n)e^-j^2π^kn/A。依据LS信道估计算法所估计出的信道传输函数为:

$\begin{matrix} \hat{H} (k) = \frac{B (k)}{C (2 k)} = \sqrt[]{\frac{A}{2}} e^{- jθ (n)} H (k) e^{j 2 πkτ / A} + \frac{W (k)}{C (2 k)} (9) \end{matrix}$

经过A点IDFT得到所估计出的时域冲激响应, 则

$\begin{matrix} \hat{h} (n) = \sqrt[]{\frac{A}{2}} e^{- jθ (n)} (h (n + τ) modA) + w (n) (10) \end{matrix}$

式中:w(n)= $\begin{matrix} \frac{1}{\sqrt[]{A}} \end{matrix} \begin{matrix} \overset{A - 1}{\sum_{k = 0}} \end{matrix} \begin{matrix} \frac{W (k)}{C (2 k)} \end{matrix}$ e^j^2π^kn/A, 其是均值为0, 方差为 $\begin{matrix} δ_{n}^{2} \end{matrix}$ /A $\begin{matrix} \overset{A - 1}{\sum_{k = 0}} \end{matrix}$ 1/ $\begin{matrix} {|C (2 k)|}^{2} \end{matrix}$ 的复高斯白噪声。

$\begin{matrix} 而 \hat{h} (n) = \frac{1}{\sqrt[]{A}} \overset{A - 1}{\sum_{k = 0}} \hat{H} (k) e^{j 2 πkn / A} (11) \end{matrix}$

由式(7)可知发端数据满足循环右移性质, 经过LS算法, 可通过式(11)求得信道的冲激响应, 由式(10)可知, 估计出的信道冲激响应也满足循环右移性质。

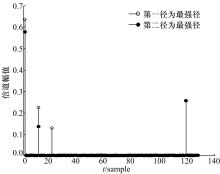
为验证信道冲激响应的循环右移性质, 图1给出了应用到SUI信道中的计算机仿真结果, 其中第一径为最强径和第二径为最强径分别表示了粗同步不存在定时偏差和存在定时偏差τ 。由图1可知, 当粗同步存在定时偏差时, 即第二径为最强径, 信道的第一径幅值则会相应地循环右移τ , 与分析结果相符。

	Figure Option View Download New Window
	图1 两种情况下的信道幅值Fig.1 Channel amplitude in two cases

1.2.2 滑动窗口法

针对信道的冲激响应窗口, 设置一个从后半部分开始的循环左移滑动窗口求其能量和。当第一径为最强径时, 随着滑动窗口的移动, 滑动窗口内的能量依次增加第1径、第2径、…、最后一径。当第i(i≥ 2)径为能量最强径时, 信道的冲激响应各径发生了循环右移, 则相应依次增加第i径、…、最后一径, 再逐渐减少第1径、第2径, 一直到第i-1径。则滑动窗口内信道冲激响应能量X(d)可以表示为:

$\begin{matrix} \begin{matrix} X_{} (d) = \overset{N'_{g} - 1}{\sum_{l = 0}} {|\hat{h} (d + l) modA|}^{2} (12) \\ A - N_{g} \leq d \leq A \end{matrix} \end{matrix}$

式中:N'_g为滑动窗口的长度。为更加明显地观测上升沿和下降沿, 即确定各径所在位置, 可通过计算X(d)与相邻值X(d+1)之差e(d), 即

$\begin{matrix} e (d) = X (d + 1) - X (d) (13) \end{matrix}$

当第i(i≥ 2)径为能量最强径时, 根据信道冲激响应的循环右移特性可知, 第一径所在位置即为滑动窗口能量变化e(d)的第一个负峰值。因此, 可通过取检测e(d)内的最小值或者与自适应门限比较判决检测第一径。

(1)最小值法

当粗同步存在定时偏差时, 采用检测e(d)窗口内的最小值来确定第一径延时所在位置, 即

$\begin{matrix} \begin{matrix} \hat{τ} = A - \arg \min_{d} {e (d) : 1 \leq d \leq A} (14) \\ d_{s} = d_{c} - \hat{τ} (15) \end{matrix} \end{matrix}$

为统一检测方法, 均通过检测e(d)窗口内的最小值, 当粗同步定时准确时, 即第一径为最强径, 在X(end)后加上X(end)× 9/10(X(end)为滑动窗口内的最后一个值的数值), 人为产生一个下降沿。

将最小值法具体应用到SUI信道模型中, 其中N'_g=N_g+1, A=128, N_g=64, X(d)和e(d)的图形如图2所示, 因SUI信道有三条径, 故当第一径为最强径时, 其存在3个上升沿和人为产生的下降沿。检测其最小值, 即检测人为产生的负峰值(第一径循环右移后所在位置), 由式(15)可知, 此时 $\begin{matrix} \hat{τ} \end{matrix}$ =0。而当第二径为最强径时, 其存在2个上升沿和2个下降沿, 第一个下降沿为粗同步存在定时偏差时, 第一径循环右移后所在位置, 第二个下降沿为人为产生的负峰值, 找到其最小值也能正确检测到第一径延时所在位置, 其与前面分析结果相符。

	Figure Option View Download New Window
	图2 滑动窗口内的能量值以及相邻值之间的变化Fig.2 Energy value and difference in sliding window

(2)自适应门限法

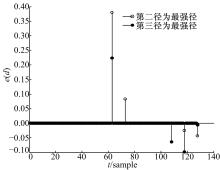
通过检测滑动窗口内能量变化的最小值提高了检测精度, 但仍存在较大的漏检, 因为其只修正了部分最强径不为第一径的情况。将最小值法具体应用到SUI信道模型为例, 仿真条件与图2相同, 可观察到其存在的漏检情况。

如图3所示, 当第二径为最强径时, 第一个负峰值即为循环右移后第一径所在位置, 此时第一径能量小于e(end)(e(end)为滑动窗口内能量变化的最后一个值的数值), 通过最小值法则存在误检。同理, 第三径为最强径时, 第一个负峰值为循环右移后第一径所在位置, 第二个负峰值为循环右移后第二径所在位置。此时第二径能量强于第一径能量, 通过最小值同样存在误检。

	Figure Option View Download New Window
	图3 滑动窗口内能量的变化e(d)Fig.3 Difference e(d) in sliding window

而最佳定时是为了准确找到第一径所在位置, 即e(d)的第一个负峰值。因此进一步采用设置阈值的方式来提高检测精度, 通过与自适应门限进行比较判决, 准确检测出第一径。

$\begin{matrix} T h res h old = δ * (\overset{A}{\sum_{d = 1}} e (d)) / A (16) \end{matrix}$

式中:δ 为一个常数, 可根据系统同步性能要求灵活设置; 考虑到能量主要集中在各条路径, 且各径的能量值远大与其他点, 故采用对e(d)求平均的方法。所求平均值与除各径外的其他样点存在较大差值, 且随着收端信号的能量变化而变化。

将e(d)与-Threshold进行比较判决, 找出第一个负峰值的位置, 设为path1, 则第一径延时所在位置即为:

$\begin{matrix} \begin{matrix} \hat{τ} = A - pat h 1 (17) \\ d_{s} = d_{c} - \hat{τ} (18) \end{matrix} \end{matrix}$

通过这种方法, 能避免最小值法存在的漏检情况下进一步提高检测精度。

2 性能验证

为了验证本文算法的性能, 参照WiMAX标准^[11], 构造了第二部分所述的训练符号的结构, 其中DFT点数N=256, 循环前缀N_g=64, 则A=N/2=128, 系统时钟为20 MHz, 自适应门限参数δ =2。本文通过定时均方误差MSE和漏检概率P_m(P_m为未精确定时到理想同步点帧数与仿真总帧数之比)来测试各算法的性能。采用的信道模型为SUI1、SUI2, 每次结果都是通过100 000次的仿真平均得到的。

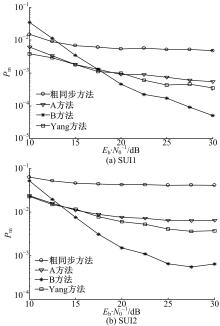
图4为4种算法的漏检概率对比图。其中粗同步方法即为文中的粗同步算法。A方法为文中粗同步和精同步结合后, 采用最小值法进行检测。B方法相对于A方法, 最终检测时采用了自适应门限法。而Yang方法^[9]为本文的对比方法。

	Figure Option View Download New Window
	图4 SUI信道下漏检概率Fig.4 Missing probability in SUI channel

由图4(a)(b)可知, A方法、B方法和Yang方法在SUI1和SUI2信道下的漏检概率均比粗同步方法小。这一结果源于:在多径衰落信道中, 粗同步算法估计的符号定时点是能量最大径的延时, 而其他3种方法均采用了精同步算法来纠正偏离第一径延时的定时点。Yang方法与A方法性能相近, 这两种算法将部分最强径不为第一径的定时点修正回到第一径, 但仍存在漏检。B方法其门限的设置与信号和噪声的能量有关, 故其检测概率会受信噪比的影响, 低信噪比下, 噪声能量较大, 部分点受噪声影响而超过门限值, 此时所取并非第一径, 造成了漏检。因此在低信噪比的情况下, SUI1和SUI2的检测性能比A方法和Yang方法略差, 但随着信噪比的提高, B方法比其他3种方法漏检概率都小, 性能更好。

图4中的漏检概率为未精确定时到理想同步点的帧数与仿真总帧数之比, 但对OFDM系统, 同步点落在CP中时, 只是相位有了恒定的偏移, 可通过信道估计得以补偿。因此, 本文进一步对比各算法在SUI1和SUI2信道下定时点的MSE结果, 如图5所示。

观察图5中(a)(b)可知, MSE曲线显示的下降趋势与漏检概率曲线一致, 符合预期结果。由仿真结果可知, A方法提高了检测精度, 因为其通过取窗口内的最小值将部分最强径不为第一径的定时点修正回到第一径。B方法门限设置更加合理, 更加灵活, 能够准确找出第一径位置, 具有更高的检测精度。

	Figure Option View Download New Window
	图5 SUI信道下MSEFig.5 MSE in SUI channel

3 结束语

针对第一径不是最强径的情况, 提出了一种基于信道估计的定时同步算法。在粗同步定到最强径的基础上, 其精同步首先依据LS算法求出信道冲激响应, 再基于其循环右移特性通过滑动窗口内能量变化判断各径所在位置, 最后采用最小值或自适应门限法准确定位出第一径。最小值法提高了检测概率, 但仍存在较大的漏检, 而针对不同信道的自适应门限法能准确定位到第一径。理论分析和仿真结果表明, 本文方法可降低符号同步的漏检概率, 提高系统的定时性能。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Schmidl T M, Cox D C. Robust frequency and timing synchronization for OFDM[J]. IEEE Transactions on Communications, 1997, 45(12): 1613-1621. [本文引用:1]
[2]	石峰, 王晨, 周柱, 等. 一种新的基于重复共轭对称构前导的 OFDM 同步算法[J]. 国防科技大学学报, 2010, 32(3): 103-108. Shi Feng, Wang Chen, Zhou Zhu, et al. A new timing synchronization method for OFDMsystems based on repeated-conjugated-symmetric preamble[J]. Journal of National Universityof Defense Technology, 2010, 32(3): 103-108. [本文引用:1]
[3]	Chan Y C, Tseng P H, Lin D B, et al. Maxi-mal power path detection for OFDM timing—advanced synchronization schemes[C]∥The 24th International Symposium on Personal In-door and Mobile Radio Communications (PIM-RC), 2013: 192-196. [本文引用:1]
[4]	Yang Fan, Zhang Xi, Yu Wei, et al. Coarse symbol timing for OFDM systems by rankingpreamble cross-correlations[C]∥The 47th Annual Conference on Information Sciences and Systems(CISS), 2013: 1-6. [本文引用:1]
[5]	刘毅, 李丹萍, 胡梅霞, 等. 低信噪比下MIMO-OFDM 系统时频同步方案[J]. 吉林大学学报: 工学版, 2008(增刊2): 250-254. Liu Yi, Li Dan-ping, Hu Mei-xia, et al. Syn-chronization for MIMO-OFDM system in low SNR environments[J]. Journal of Jilin Univer-sity(Engineering and Technology Edition), 2008(Sup. 2): 250-254. [本文引用:1]
[6]	Udupa P, Sentieys O, Scalart P. A block-para-llel architecture for initial and fine synchroni-zation in OFDM systems[C]∥IEEE International Conference on Communications (ICC), 2013: 4761-4765. [本文引用:1]
[7]	Abdzadeh-Ziabari H, Shayesteh M G. Robust timing and frequency synchronization for OFDM systems[J]. IEEE Transactions on Vehicular Technology, 2011, 60(8): 3646-3656. [本文引用:1]
[8]	Kung T L, Parhi K K. Optimized joint timing synchronization and channel estimation for OFDM systems[J]. IEEE Wireless Communications Letters, 2012, 1(3): 149-152. [本文引用:1]
[9]	Yang Fan, Zhang Xi. Robust time domain fine symbol synchronization for OFDM-based packet transmission using CAZAC preamble[C]∥Military Communications Conference, 2013: 436-440. [本文引用:1]
[10]	Kishore C N, Reddy V. A technique for dominant path delay estimation in an OFDM system and its application to frame synchronization in OFDM mode of WMAN[J]. EURASIP Journal on Wireless Communications and Networking, 2006: 86147. [本文引用:1]
[11]	Jinsha Y, Hongmei S. A modified symbol timing synchronization algorithm for WiMAXOFDM systems[C]∥IEEE Pacific-Asia Workshop on Computational Intelligence and Industrial Application(PACIIA), 2008: 748-751. [本文引用:1]