P2P节点在线机制的纳什均衡和社会最优策略

引用本文

金顺福, 李洋, 刘建平, 霍占强. P2P节点在线机制的纳什均衡和社会最优策略. 吉林大学学报: 工学版, 2016, 46(1): 296-302
JIN Shun-fu, LI Yang, LIU Jian-ping, HUO Zhan-qiang. Strategies of Nash equilibrium and social optimization for online mechanisms of P2P nodes. Journal of Jilin University Engineering and Technology Edition, 2016, 46(1): 296-302 复制到剪切板

Permissions

P2P节点在线机制的纳什均衡和社会最优策略

金顺福^1,², 李洋^1,², 刘建平^1,², 霍占强³

1.燕山大学信息科学与工程学院,河北秦皇岛 066004

2.河北省计算机虚拟技术与系统集成重点实验室,河北秦皇岛 066004

3.河南理工大学计算机科学与技术学院,河南焦作 454000

霍占强(1979-),男,副教授,博士.研究方向:网络通信技术.E-mail:hzq@hpu.edu.cn

作者简介:金顺福(1966-),女,教授,博士生导师.研究方向:通信系统建模理论.E-mail:jsf@ysu.edu.cn

基金:国家自然科学基金项目(61472342,11201408); 河北省自然科学基金项目(2012203093)

摘要

针对P2P网络中节点均追求个人收益的最大化导致系统收益不能达到社会最优的问题,提出向请求节点征收接入费用的方案。依据P2P网络节点的在线机制,建立服务台数随机变化的连续时间排队模型,采用矩阵几何解方法,基于不可观察排队规则进行系统模型的稳态分析,给出节点平均延迟以及节点激活率等指标的表达式。构造收益函数,分析节点在线机制的纳什均衡策略和社会最优策略,通过合理的收费方案,实现P2P网络的社会最优。

关键词: 通信技术; P2P网络; 在线机制; 矩阵几何解; 纳什均衡; 社会最优

中图分类号:TP393 文献标志码:A 文章编号:1671-5497(2016)01-0296-07

Strategies of Nash equilibrium and social optimization for online mechanisms of P2P nodes

JIN Shun-fu^1,², LI Yang^1,², LIU Jian-ping^1,², HUO Zhan-qiang³

1.School of Information Science and Engineering, Yanshan University, Qinhuangdao 066004, China

2.Key Laboratory for Computer Virtual Technology and System Integration of Hebei Province, Qinhuangdao 066004, China

3.College of Computer Science and Technology, Henan Polytechnic University, Jiaozuo 454000, China

Abstract

In P2P networks, due to the selfish behavior, all the nodes pursue the maximum individual gains, but the system cannot achieve socially optimal gain. To solve this problem, a charging scheme to the requesting nodes is proposed. Based on the online mechanism of the P2P nodes, a continuous time queuing model with random number of services is built. Using the method of a matrix-geometric solution, the system model is analyzed in steady state based on an unobservable queuing rule. The expressions of the average delay and activation ratio are given. By establishing a reward function, the strategies with Nash equilibrium and social optimization are investigated. With a reasonable pricing policy the P2P network is socially optimized.

Keyword: communication; P2P networks; online mechanism; matrix-geometric solution; Nash equilibrium; social optimization

Show Figures

0 引言

P2P网络用较低的成本聚合海量资源, 使更多的用户参与到互联网中, 对互联网的迅速成长与普及起到了至关重要的作用^[1]。P2P节点是对等的关系, 既可以作为服务节点将自身的资源共享, 被其他节点访问; 也可以作为访问节点, 共享网络中其他节点的资源^[2]。P2P节点普遍存在自私行为, 均追求个人利益最大化, 导致出现只请求资源不提供服务的“ 搭便车” 现象, 严重影响了P2P网络的性能和运行^{[3, 4]}。因此, 调节节点的行为对P2P网络的优化十分重要。

近年来, 部分学者基于激励机制^[5]研究了P2P网络中的节点在线行为。按照工作方式, 激励机制可以分为虚拟货币激励机制和非货币激励机制。文献[6]提出了一种基于电子票券和全局信誉度的激励机制。根据节点的信誉度, 以有偿服务的方式控制节点的行为, 激励节点更好地提供服务。文献[7]提出了一种以货易货的资源配置机制, 该机制下节点之间是激励相容的, 每个节点只有采取诚实行为提供相应的服务或者资源, 才能获得等值的回报。文献[8]提出了另外一种基于激励机制的优化方法, 即差分服务机制。根据节点提供的不同服务, 系统中的服务器通过衡量节点的贡献值, 对节点给予不同的服务值。还有人将经济学中的博弈论应用于P2P网络的研究中。文献[9]提出了一种基于博弈策略的研究模型, 对系统中的节点进行量化分析, 在随机博弈收益矩阵的基础上, 通过调整相关参数引导节点行为。文献[10]结合博弈论, 提出了一种新型的激励机制(Novel incentive mechanism)。考虑网络中的有用信息和P2P节点对网络性能的影响因素, 利用博弈论定义节点的策略空间, 找出节点的纳什均衡, 以控制节点的自私行为。

综合已有的文献可以看出, 已有的研究均未考虑P2P节点的排队现象。本文结合连续时间随机理论和博弈论, 从不可观察排队的角度出发, 建立节点在线机制的系统模型。进行纳什均衡策略和社会最优策略的研究, 面向节点给出合理的收费方案, 抑制节点的自私行为, 实现网络最优。

1 系统模型与性能分析

1.1 连续时间排队模型

在P2P网络中, 节点的上线过程是随机的, 在线时间也是随机的, 因此, 任意时刻在线节点数量为随机变量。依节点在线机制建立服务台数随机变化的连续时间排队模型。

假设系统中提供某一服务的节点数量为N。令n_c(t)=i, i∈ {0, 1, 2, …}表示时刻t向网络发出服务请求的节点个数; 令n_s(t)=j, j∈ {0, 1, 2, …, N}表示时刻t网络中提供服务的在线节点个数。{n_c(t), n_s(t)}构成二维随机过程, 其状态空间Ω 为:

$\begin{matrix} Ω = \{(i, j) | i = 1, 2, \dots; j = 1, 2, \dots, N\} \end{matrix}$

假设请求节点的到达过程服从参数为λ _c(λ _c> 0)的泊松分布, 传输时间服从参数为μ _c(μ _c> 0)的指数分布; 服务节点的上线过程服从参数为λ _s(λ _s> 0)的泊松分布, 在线时间服从参数为μ _s(μ _s> 0)的指数分布。假设任意两个在线节点提供的传输服务相互独立。综合上述假设条件, {n_c(t), n_s(t)}为Markov过程。

1.2 转移率矩阵

针对特定服务, 当系统中请求节点的个数为i(i≥ 0)时, 称系统处于i水平。在相同水平下, 考虑系统中在线节点个数j(0≤ j≤ N)的状态变化。当系统中在线节点个数为j时, 下一时刻可能由于节点离线, 在线节点个数减少一个; 也可能既没有节点上线也没有节点离线, 在线节点个数保持不变; 还可能由于新节点上线, 在线节点个数增加一个。

综合以上的分析结果, 构造系统在同一水平下的状态转移率矩阵T如下:

$\begin{matrix} \begin{matrix} T = \\ (\begin{matrix} - N λ_{s} & N λ_{s} \\ μ_{s} & - (N - 1) λ_{s} - μ_{s} & (N - 1) λ_{s} \\ ⋱ & ⋱ & ⋱ \\ (N - 1) μ_{s} & - (N - 1) μ_{s} - λ_{s} & λ_{s} \\ N μ_{s} & - N μ_{s} \end{matrix}) \end{matrix} \end{matrix}$

令A_i为系统水平保持不变的转移率矩阵, 则:

$\begin{matrix} A_{i} = \{\begin{matrix} T + diag (- λ_{c}), i = 0 \\ T + diag (- λ_{c} - \min (i, j) μ_{c}), \\ 1 \leq i \leq N - 1 \\ T + diag (- λ_{c} - j μ_{c}), i \geq N \end{matrix} \end{matrix}$

令B_i为系统水平由i到i-1的转移率矩阵, 则:

$\begin{matrix} B_{i} = \{\begin{matrix} diag (0, \min (i, j) μ_{c}, L, \min (i, N) μ_{c}), \\ 1 \leq i \leq N - 1 \\ diag (0, μ_{c}, 2 μ_{c}, L, N μ_{c}), i \geq N \end{matrix} \end{matrix}$

当i≥ N时, 矩阵A_i和B_i均保持不变。矩阵A_i, i≥ N用A表示, 矩阵B_i, i≥ N用B表示。

令C为系统水平由i到i+1的转移率矩阵, 则:

C=diag $\begin{matrix} (λ_{c}, \dots, λ_{c}) \end{matrix}$

矩阵A_i、A、B_i、B、C均为N+1阶方阵。令Q为二维连续时间Markov链 $\begin{matrix} \{n_{c} (t), \end{matrix} \begin{matrix} n_{s} (t)\} \end{matrix}$ 的转移率矩阵, 依系统水平的字典顺序, 矩阵Q可表示成如下分块三对角形式。

$\begin{matrix} Q = (\begin{matrix} A_{0} & C \\ B_{1} & A_{1} & C \\ ⋱ & ⋱ & ⋱ \\ B_{N - 1} & A_{N - 1} & C \\ B & A & C \\ ⋱ & ⋱ & ⋱ \end{matrix}) (1) \end{matrix}$

1.3 稳态分布

定义二维Markov链 $\begin{matrix} \{n_{c} (t), n_{s} (t)\} \end{matrix}$ 的稳态概率分布为π _i_,_j, 即π _i_,_j= $\begin{matrix} \lim_{t \to \infty} \end{matrix}$ P{n_c(t)=i, n_s(t)=j}。令稳态下系统处于i水平的概率向量为π _i, 即π _i= $\begin{matrix} (π_{i, 0}, π_{i, 1}, \dots, π_{i, N}) \end{matrix}$ 。

根据转移率矩阵Q的分块结构特点, 将稳态分布向量写成分块形式, 表示如下:

π = $\begin{matrix} (π_{0}, π_{1}, π_{2}, \dots) \end{matrix}$

由转移率矩阵结构可知, 二维Markov过程 $\begin{matrix} \{n_{c} (t), n_{s} (t)\} \end{matrix}$ 是一个拟生灭过程, 因此, 可以利用矩阵几何解方法求解系统的稳态分布。构造方程组:

$\begin{matrix} \begin{matrix} \{\begin{matrix} (π_{0}, π_{1}, \dots, π_{N}) B [R] = 0 \\ \overset{N - 1}{\sum_{i = 0}} π_{i} e + π_{N} {(I - R)}^{- 1} e = 1 \\ π_{i} = π_{N} R^{i - N}, i \geq N \end{matrix} (2) \\ 式中 : \\ B [R] = (\begin{matrix} A_{0} & C \\ B_{1} & A_{1} & C \\ ⋱ & ⋱ & ⋱ \\ B_{N - 1} & A_{N - 1} & C \\ B & RB + A \end{matrix}) (3) \end{matrix} \end{matrix}$

R是方程R²B+RA+C=0的最小非负解, 并且R的谱半径小于1。基于方程R=- $\begin{matrix} (C + R^{2} B) \end{matrix}$ A^-¹, 采用迭代方法求R的近似解。将R代入式(2)和式(3)可以进一步解出稳态分布向量π 。

1.4 系统性能指标

请求节点的平均延迟W(λ _c)表示请求服务的节点在系统中的平均逗留时间。在线节点的数量代表着P2P网络的服务质量。在线节点数目越多, 系统的服务质量越高, 请求节点的平均延迟越短。反之, 在线节点越少, 系统的服务质量越低, 请求节点的平均延迟越长。稳态下, P2P网络的平均队长E $\begin{matrix} [L] \end{matrix}$ 为:

$\begin{matrix} E [L] = \overset{\infty}{\sum_{i = 0}} i \overset{N}{\sum_{j = 0}} π_{i, j} (4) \end{matrix}$

利用Little公式, 请求节点的平均延迟W(λ _c)可以表示为关于λ _c的函数:

$\begin{matrix} W (λ_{c}) = \frac{1}{λ_{c}} \overset{\infty}{\sum_{i = 0}} i \overset{N}{\sum_{j = 0}} π_{i, j} (5) \end{matrix}$

节点激活率β 定义为稳态下P2P网络中某节点处于在线状态的概率。节点激活率体现了在线节点的积极性。在线节点的积极性越高, 节点激活率越大。反之, 在线节点的积极性越低, 节点激活率越小。在线节点状态独立于请求节点状态。节点激活率β 表示为:

$\begin{matrix} β = \frac{λ_{s}}{λ_{s} + μ_{s}} (6) \end{matrix}$

2 P2P网络的收费方案

在实际的P2P网络中, 请求节点加入队列之前可能并不知道队列的内部信息, 比如系统已有的请求节点个数或在线节点个数。本文基于不可观察排队模型^{[11, 12, 13]}研究P2P网络请求节点的纳什均衡到达率、社会最优到达率及收费策略。

2.1 纳什均衡策略

根据节点在线机制对服务台数随机变化的连续时间排队模型做以下假设:

(1)请求节点在决定是否进入系统时, 不能观察到缓存中的队列长度, 且一旦进入系统之后不允许中途离开。

(2)一个请求节点完成传输对应的回报为R。

(3)请求节点加入队列后, 延迟单位时间所产生的成本为f_W₁。节点在线单位时间所产生的费用为f_W₂。

(4)所有单个节点的净收益函数是相同的, 并且是可加的。

基于上述假设, 定义单个节点的平均净收益为:

$\begin{matrix} U_{i} = R - f_{W 1} W (λ_{c}) - f_{W 2} β (7) \end{matrix}$

P2P网络中, 大部分节点都希望从网络中获取数据或者服务, 同时, 又不希望贡献自身的资源。但是, 请求节点越多, 节点在系统中平均延迟越长, 其净收益就越小。显然, 个人收益函数U_i是单调减函数。根据式(7)可知, 净收益U_i的值为0的点为纳什均衡点, 此时的到达率是纳什均衡到达率λ _e, 则:

$\begin{matrix} W (λ_{e}) = (R - f_{W 2} β) / f_{W 1} (8) \end{matrix}$

2.2 社会最优策略

针对社会最优策略的分析, 要考虑每个时刻系统中节点的平均净收益。不考虑系统对节点征收的接入费用, 则社会平均净收益U_s表示为:

$\begin{matrix} U_{s} = λ_{c} (R - f_{W 1} W (λ_{c}) - f_{W 2} β) (9) \end{matrix}$

社会最优的目标是最大化系统中所有节点的总收益, 因此, 社会收益最大时的到达率是社会最优请求到达率。令λ ^*表示社会最优策略下请求节点的到达率, 则:

$\begin{matrix} λ^{*} = \arg \max_{0 \leq λ_{c} < 1} (λ_{c} (R - f_{W 1} W (λ_{c}) - f_{W 2} β)) (10) \end{matrix}$

2.3 收费策略

因为平均延迟W $\begin{matrix} (λ_{c}) \end{matrix}$ 是单调递增函数, 所以W' $\begin{matrix} (λ_{c}) \end{matrix}$ > 0。利用式(9)对λ _c求导, 令导数为0, 则:

W $\begin{matrix} (λ^{*}) \end{matrix}$ +λ _cW' $\begin{matrix} (λ^{*}) \end{matrix}$ = $\begin{matrix} (R - f_{W 2} β) \end{matrix}$ /f_W₁ (11)

比较式(8)与式(11), 可得W $\begin{matrix} (λ_{e}) \end{matrix}$ > W $\begin{matrix} (λ^{*}) \end{matrix}$ 。考虑W $\begin{matrix} (λ_{c}) \end{matrix}$ 是λ _c的单调增函数, 则有λ _e> λ ^*, 即纳什均衡策略下将有更多的请求节点到达。

为了实现P2P网络的社会最优, 抑制节点的自私行为, 适当降低请求节点的到达率, 对请求节点征收合理的接入费用p, 并重新定义单个节点的平均净收益如下:

$\begin{matrix} U_{i} = R - f_{W 1} W (λ_{c}) - f_{W 2} β - p (12) \end{matrix}$

令U_i=0, 可得纳什均衡策略下的接入费用

$\begin{matrix} p = R - f_{W 1} W (λ^{*}) - f_{W 2} β (13) \end{matrix}$

社会最优的目的是为了最大化系统中全部节点的总收益, 而单位时间内社会平均净收益U_s表示为:

$\begin{matrix} \begin{matrix} U_{s} = λ_{c} p + λ_{c} (R - f_{W 1} W (λ_{c}) - f_{W 2} β - p) = \\ λ_{c} (R - f_{W 1} W (λ_{c}) - f_{W 2} β) \end{matrix} (14) \end{matrix}$

由式(14)可知, 系统对请求节点征收接入费用并不影响社会平均净收益。实际上, 从社会角度来看, 征收的接入费用只是在P2P节点之间转移了部分收益, 并不影响总体的收益, 即社会最优到达率不变。但是, 征收接入费用后个人收益降低, 也就是说纳什均衡到达率变小, 当p=R-f_W₁W $\begin{matrix} (λ^{*}) \end{matrix}$ -f_W₂β 时, 请求节点的纳什均衡到达率与社会最优请求到达率一致。

3 仿真验证

针对不同的传输回报R, 逗留成本f_W₁, 激活费用f_W₂, 系统服务节点个数N, 请求节点传输率μ _c, 服务节点到达率λ _s与离去率μ _s, 进行纳什均衡策略、社会最优策略及收费策略的仿真验证。

3.1 纳什均衡策略

由式(7)可知, 当R-f_W₁W $\begin{matrix} (λ_{c}) \end{matrix}$ -f_W₂β =0时, 系统所对应的请求节点到达率λ _c即为纳什均衡策略下的到达率λ _e。设定请求节点到达率的精确度为0.01, 纳什均衡策略下的请求节点个人到达率λ _e的取值范围如表1所示。

表1 纳什均衡策略下的请求节点到达率 Table 1 Arrival rate of requesting node with Nash equilibrium strategy

3.2 社会最优策略

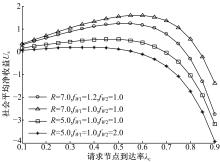
以N=4, μ _c=0.40, λ _s=0.006, μ _s=0.0010为例, 针对不同的传输回报R, 逗留成本f_W₁及激活费用f_W₂, 社会平均净收益U_s随请求节点到达率λ _c的变化趋势如图1所示。

	Figure Option View Download New Window
	图1 不同R、f_W₁和f_W₂下的社会平均净收益U_sFig.1 Socially average net reward U_s with different R, f_W₁ and f_W₂

由图1可以看出, 对于一定的请求节点到达率λ _c, 逗留成本f_W₁及激活费用f_W₂, 随着回报R的增大, 请求节点因完成传输得到的回报增大, 单个请求节点的净收益随之增加, 社会平均净收益提升。随着逗留成本或激活费用的提高, 发出服务请求的节点因在系统中逗留产生的成本, 或者P2P节点由于提供服务引起的费用增加, 导致单个节点的平均净收益减少, 社会平均净收益降低。

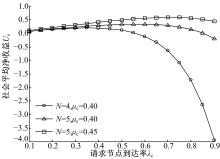
以R=5.0, f_W₁=1.0, f_W₂=2.0, λ _s=0.006, μ _s=0.0010为例, 针对不同的服务节点个数N和请求节点传输率μ _c, 社会平均净收益U_s随请求节点到达率λ _c的变化趋势如图2所示。

	Figure Option View Download New Window
	图2 不同N和μ _c下的社会平均净收益U_sFig.2 Socially average net reward U_s with different N and μ _c

由图2可以看出, 对于一定的请求节点到达率λ _c和传输率μ _c, 服务节点个数N越大, 系统中在线节点个数越多, 请求节点因逗留而产生的成本越小, 因此, 社会平均净收益呈上升趋势。当请求节点到达率λ _c和服务节点个数N固定时, 因为请求节点传输率的增大, 系统中其他请求节点在缓存中消耗的时间减少, 成本降低, 社会平均净收益增加。

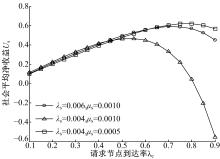
以R=5.0, f_W₁=1.0, f_W₂=2.0, N=5, μ _c=0.45为例, 针对不同的服务节点到达率λ _s和离去率μ _s, 社会平均净收益U_s随请求节点到达率λ _c的变化趋势如图3所示。

	Figure Option View Download New Window
	图3 不同λ _s和μ _s下的社会平均净收益U_sFig.3 Socially average net reward U_s with different λ _s and μ _s

由图3可以看出, 当在线节点离去率μ _s和请求节点到达率λ _c不变时, 社会平均净收益U_s随着在线节点到达率λ _s的增大而增大。这是因为在线节点到达率的增加会引起系统中在线节点个数的增多, 系统的服务质量提高, 请求节点在系统中逗留时间因此减少, 社会平均净收益随之增加。在线节点到达率λ _s和请求节点到达率λ _c不变的情况下, 社会平均净收益U_s随着在线节点离去率μ _s的减小而增加。这是因为在线节点离去率越小, 稳态下网络中的在线节点个数越多, P2P网络的传输能力越强, 请求节点在系统中将延迟更少的时间, 逗留成本下降, 社会平均净收益提升。

由图1~图3还可以看出, 在其他参数保持不变的情况下, 随着请求节点到达率λ _c的增加, 社会平均净收益U_s曲线呈现先上升后下降的趋势。当请求节点到达率的整体水平较低时, 随着请求节点到达率的增加, 能从网络中获得回报的节点数增多, 社会平均净收益呈上升趋势。当请求节点到达率的整体水平较高时, 随着请求节点的增多, 节点的平均逗留时间增加, 逗留成本增加, 社会平均净收益呈下降趋势。综合这两种趋势可知, 社会平均净收益存在一个最大值。

不同系统参数下的社会最优请求到达率的数值结果如表2所示。

表2 社会最优策略下数值结果 Table 2 Numerical results with socially optimal strategy

3.3 收费策略

比较表1中纳什均衡请求到达率的下限与表2中社会最优请求到达率, 进一步验证了λ _e> λ ^*。基于以上实验中的系统参数, 利用式(13), 对请求节点征收的接入费用p如表3所示。

表3 P2P网络接入费用的数值结果 Table 3 Numerical results for admission fee in P2P networks

4 结束语

根据P2P节点的在线机制建立了服务台数随机变化的连续时间排队模型, 给出了节点平均延迟和节点激活率的表达式。通过收益函数, 揭示了纳什均衡请求到达率大于社会最优请求到达率, 并面向请求节点制定了收费方案。实验结果表明, 本文给出的收费方案可以有效调整请求节点的到达方式, 实现P2P网络的社会最优。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	张玉洁, 何明, 孟祥武. 基于用户需求的内容分发点对点网络系统研究[J]. 软件学报, 2014, 25(1): 98-117. Zhang Yu-jie, He Ming, Meng Xiang-wu. Research on CDN-P2P system over user requirements[J]. Journal of Software, 2014, 25(1): 98-117. [本文引用:1]
[2]	陈绵书, 王世朋, 陈贺新, 等. 改进的基于推荐证据的对等网络信任模型[J]. 吉林大学学报: 工学版, 2013, 43(6): 1666-1674. Chen Mian-shu, Wang Shi-peng, Chen He-xin, et al. Improved trust model based on recommendation evidence for P2P networks[J]. Journal of Jilin University(Engineering and Technology Edition), 2013, 43(6): 1666-1674. [本文引用:1]
[3]	余一娇, 金海. 对等网络中的搭便车行为分析与抑制机制[J]. 计算机学报, 2008, 31(1): 1-15. Yu Yi-jiao, Jin Hai. A survey on overcoming free riding in Peer-to-Peer networks[J]. Chinese Journal of Computers, 2008, 31(1): 1-15. [本文引用:1]
[4]	马喜强, 宋喜佳, 刘维亚, 等. 非平稳服务请求下的功耗管理[J]. 光学精密工程, 2014, 22(7): 1929-1937. MA Xi-qiang, Song Xi-jia, Liu Wei-ya, et al. Power-aware management for non-stationary service requests[J]. Optics and Precision Engineering, 2014, 22(7): 1929-1937. [本文引用:1]
[5]	Wu Y, Zhou B, Dong X, et al. A P2P streaming media data transmission strategy based on incentive mechanism[C]∥International Conference on Computer Science and Service System, Nanjing, 2011: 3814-3817. [本文引用:1]
[6]	徐小龙, 熊婧夷, 杨庚, 等. 基于电子票券和全局信誉度的P2P激励机制[J]. 北京理工大学学报, 2011, 31(10): 1236-1241. Xu Xiao-long, Xiong Jing-yi, Yang Geng, et al. P2P incentive mechanism based on electronic coupons combined with global reputation values[J]. Transactions of Beijing Institute of Technology, 2011, 31(10): 1236-1241. [本文引用:1]
[7]	Hu Y S, Dong D F, Li J, et al. Efficient and incentive-compatible resource allocation mechanism for P2P-assisted content delivery systems[J]. Future Generation Computer Systems, 2013, 29(6): 1611-1620. [本文引用:1]
[8]	温琼翡, 朱艳琴, 纪其进. P2P流媒体系统激励机制设计与分析[J]. 小型微型计算机系统, 2013, 34(5): 959-963. Wen Qiong-fei, Zhu Yan-qin, Ji Qi-jin. Design and analysis of incentive mechanism for P2P-VOD systems[J]. Journal of Chinese Computer Systems, 2013, 34(5): 959-963. [本文引用:1]
[9]	王春枝. 对等网络中节点合作激励机制研究[D]. 武汉: 武汉理工大学计算机科学与技术学院, 2013. Wang Chun-zhi. Research on incentive mechanism for nodes cooperation in Peer-to-Peer networks[D]. Wuhan: School of Computer Science and Technology, Wuhan University of Technology, 2013. [本文引用:1]
[10]	Wu T Y, Lee W S, Guizani N, et al. Incentive mechanism for P2P file sharing based on social network and game theory[J]. Network and Computer Applications, 2014, 41(1): 47-55. [本文引用:1]
[11]	董恩清, 乔富龙, 邹宗骏, 等. 能量有效的分布式链路调度协议[J]. 光学精密工程, 2014, 22(2): 474-480. Dong En-qing, Qiao Fu-long, Zou Zong-jun, et al. Energy efficient distributed link scheduling protocol[J]. Optics and Precision Engineeri, 2014, 22(2): 474-480. [本文引用:1]
[12]	Hassin R, Haviv M. To Queue or not to Queue: Equilibrium Behavior in Queueing Systems[M]. Boston: Kluwer Academic Press, 2003. [本文引用:1]
[13]	Jin S, Zhao Y, Yue W, et al. Performance analysis of a P2P storage system with a lazy replica repair policy[J]. Journal of Industrial and Management Optimization, 2014, 10(1): 151-166. [本文引用:1]

2014

0.0

... 0 引言P2P网络用较低的成本聚合海量资源,使更多的用户参与到互联网中,对互联网的迅速成长与普及起到了至关重要的作用^[1] ...

2013

0.0

. 2013, 43(6):1666-1674 DOI:10.7964/jdxbgxb201306037

Improved trust model based on recommendation evidence for P2P networks

改进的基于推荐证据的对等网络信任模型

Chen Mian-shu , Wang Shi-peng , Chen He-xin

陈绵书, 王世朋, 陈贺新

College of Communication Engineering, Jilin University, Changchun 130022, China

An improved trust model based on recommendation evidence for P2P network is proposed. The aim of the model is to resolve the problem of identifying dishonesty recommendation peers in traditional trust model for unstructured P2P network. The new model updates the trust records of the transaction node and recommendation nodes simultaneously according to the transaction results. It adopts the decay function, which meets interpersonal characteristics, to describe the decay process of the trust records. The D-S evidence theory is introduced to the computation of the trust model, which integrates direct evidence and recommendation evidence into trust evidence. The model searches trust evidence through probability based Gossip algorithm. The experiment results show that the proposed model can increase the successful transaction rate and improve the network environment.

针对传统P2P对等网络信任模型中推荐节点诚实性难以判别的问题,提出了改进的基于推荐证据的P2P网络信任模型。模型根据交易结果,同时更新交易节点和推荐节点的信任记录。采用符合人际交往特性的衰减函数描述信任证据的衰减过程。将D-S证据理论应用于信任模型的信任计算中,将直接证据和推荐证据合成做为信任证据。模型采用基于概率Gossip算法实现信任证据的搜索。试验结果表明:本文算法有效地提高了P2P网络的成功交易率,改善了网络环境。

... 也可以作为访问节点,共享网络中其他节点的资源^[2] ...

2008

0.0

... 现象,严重影响了P2P网络的性能和运行^[3,4] ...

2014

0.0

... 现象,严重影响了P2P网络的性能和运行^[3,4] ...

2011

0.0

... 近年来,部分学者基于激励机制^[5]研究了P2P网络中的节点在线行为 ...

2011

0.0

2013

0.0

2013

0.0

. 2013, 34(5):959-963

Design and analysis of incentive mechanism for P2P-VOD systems

P2P流媒体系统激励机制设计与分析

Wen Qiong-fei , Zhu Yan-qin , Ji Qi-jin.

温琼翡, 朱艳琴, 纪其进

1(School of Computer Science and Technology, Soochow University, Suzhou 215006, China),2(Provincial Key Laboratory for Computer Information Processing Technology, Soochow University, Suzhou 215006, China)

Due to the existence of massive selfish nodes, free-riding and tragedy of common are serious in P2P-VOD systems.How to promote these selfish nodes to contribute their upload resources to the system and the other peers is a critical problem in P2P-VOD systems. In this paper, we design an incentive mechanism based on game theory to solve the above problem. From differential service model, the contribution value is introduced to incent nodes upload resources spontaneously; in the other hand, we proved that this mechanism exist a nash equality and find out the solution of the nash equality based on game theory. The simulation result and numerical analysis show that our mechanism can incent nodes to upload video data effectively. Furthermore, it can improve the overall resources sharing in the whole systems and maximize the system utility.

在P2P系统中，由于大量自私节点的存在，导致系统中存在公共的悲剧和搭便车现象.如何使节点能够自发的共享自身所拥有的数据资源严重困扰着P2P系统.针对这一问题，提出一种基于博弈论的P2P视频点播激励机制.通过采用差分服务方式，引入贡献值这一概念来激励节点积极上传资源；并基于博弈论的知识对所提机制进行分析，证明所提机制存在纳什均衡并求解出该纳什均衡.模拟实验和相关数据分析表明，该策略能有效的激励节点上传视频数据，改进了P2P网络中的资源共享，从而最大化系统的效用.

2013

0.0

2014

0.0

2014

0.0

... 本文基于不可观察排队模型^[11,12,13]研究P2P网络请求节点的纳什均衡到达率、社会最优到达率及收费策略 ...

2003

0.0

... 本文基于不可观察排队模型^[11,12,13]研究P2P网络请求节点的纳什均衡到达率、社会最优到达率及收费策略 ...

2014

0.0

... 本文基于不可观察排队模型^[11,12,13]研究P2P网络请求节点的纳什均衡到达率、社会最优到达率及收费策略 ...