具有固定反馈权的自适应宽带波束形成器设计

引用本文

吴凯, 苏涛, 靳标, 杨涛. 具有固定反馈权的自适应宽带波束形成器设计. 吉林大学学报: 工学版, 2016, 46(1): 303-310
WU Kai, SU Tao, JIN Biao, YANG Tao. Design of adaptive broadband beamformer with fixed feedback weights. Journal of Jilin University Engineering and Technology Edition, 2016, 46(1): 303-310 复制到剪切板

Permissions

具有固定反馈权的自适应宽带波束形成器设计

吴凯, 苏涛, 靳标, 杨涛

西安电子科技大学雷达信号处理国家重点实验室,西安 710071

作者简介:吴凯(1990-),男,博士研究生.研究方向:宽带阵列信号处理.E-mail:ookaykay@163.com

基金:国家自然科学基金项目(61271291,61201285); 教育部新世纪优秀人才支持计划项目(NCET-09-0630)

摘要

将一条具有固定系数的反馈支路引入广义旁瓣相消器(Generalized sidelobe canceller, GSC),设计了一种新的自适应宽带波束形成器。通过逼近包含干扰频带的带通滤波器,离线设计最优反馈权。研究了波束形成器的干扰抑制能力与反馈支路极点个数之间的关系。与现有含反馈波束形成器的仿真对比结果表明:由于本文波束形成器的前向支路与传统GSC相同,降低了自适应权更新的复杂性和运算量;无需极点的自适应更新,具有固有稳定性;极点个数灵活可变,增强了干扰抑制能力。

关键词: 信息处理技术; 宽带自适应波束形成; 广义旁瓣相消; 固定反馈权; 信号和干扰噪声比

中图分类号:TN958.92 文献标志码:A 文章编号:1671-5497(2016)01-0303-08

Design of adaptive broadband beamformer with fixed feedback weights

WU Kai, SU Tao, JIN Biao, YANG Tao

National Lab of Radar Signal Processing, Xidian University, Xi'an 710071, China

Abstract

By introducing a feedback branch with fixed weights, a new adaptive broadband beamformer based on the Generalized Sidelobe Canceller (GSC) is designed. The feedback weights are obtained off-line through approximating the band-pass filter whose passband covers that of the interference. Also, the relationship between the interference suppression capability of the beamformer and the number of poles of the feedback branch is investigated. Compared with existing beamformer, since the feedforward branch of the new beamformer is exactly the same as the GSC, the complexity and amount of calculations of the updating procedure for feedforward weights are reduced. Meanwhile, the fixed feedback weights guarantee its stability. Besides, the flexibility of changing the number of poles strengths its interference suppression capability.

Keyword: information processing; broadband adaptive beamforming; generalized sidelobe canceller; fixed feedback weights; signal to interference pulse noise ratio

Show Figures

0 引言

宽带波束形成器广泛应用于雷达^[1]、声呐^[2]和通信^[3]等技术领域。Frost类^{[4, 5, 6]}和广义旁瓣相消(Generalized sidelobe canceller, GSC)类^{[6, 7, 8]}是两种传统的时域自适应宽带波束形成器结构。由于只包含由抽头延迟线(Tapped delay line, TDL)组成的有限冲激响应(Finite impulse response, FIR)滤波器作为前向支路, 随着信号带宽的增加, 所需FIR滤波器的阶数, 即TDL的数量也随之增加^[9], 以获得预期的信号和干扰噪声比(Signal to interference pulse noise ratio, SINR)。文献[10-12]设计了几种新型自适应宽带波束形成器, 通过引入反馈支路, 有效地抑制了TDL随带宽的增加。基于Frost波束形成器, 文献[10, 11]设计的DUAN波束形成器, 将各个前向支路中的TDL全部替换成一阶或二阶无限冲激响应(Infinite impulse response, IIR)滤波器(采用相同的方法, 文献[11]还设计了基于GSC结构的DUAN波束形成器), 采用迭代高斯牛顿法(Recursive Gauss Newton, RGN)实现自适应权和IIR滤波器极点的迭代更新。与传统最小均方算法相比, 实现了更快的收敛速度和更好的稳态性能。然而, 极点的迭代使DUAN波束形成器可能陷入不稳定状态, 无法收敛。为了解决DUAN波束形成器的稳定性问题, 文献[12]设计了基于拉盖尔滤波器的自适应宽带波束形成器, 将各个前向支路中的TDL全部换成拉盖尔滤波器, 并离线确定拉盖尔滤波器的最优极点。DUAN和拉盖尔波束形成器将全部TDL换成IIR滤波器, 增加了权值迭代更新过程的复杂性, 降低了收敛速度。为了防止波束形成器的自适应过程陷入不稳定状态, DUAN波束形成器需要进行极点控制, 而拉盖尔波束形成器虽然极点固定, 但只包含单个极点, 使两者的干扰抑制能力均受到限制。

为了简化权值迭代更新过程, 加快收敛并增强波束形成器的干扰抑制能力, 本文基于GSC波束形成器设计一种新的时域自适应宽带波束形成器, 在保持前向支路不变的情况下, 仅引入一条具有固定权值的反馈支路, 采用一种最优迭代零极点系统识别方法^[13]离线获取最优反馈权。由于前向支路与传统GSC结构相同, 可以采用无约束优化算法进行权系数的迭代更新。以上特征使本文设计的自适应宽带波束形成器具有固有稳定性和运算量低的特点。在采用相同仿真参数及自适应算法条件下, 仿真对比了本文波束形成器与GSC、DUAN和拉盖尔波束形成器的干扰抑制能力。定量分析了实现相同SINR改善时, 4种波束形成器单次迭代的运算量。并研究了本文波束形成器反馈支路的极点个数与干扰抑制能力之间的关系。最后, 仿真验证了本文波束形成器的稳定性。

1 现有时域宽带自适应波束形成器

图1给出了传统GSC波束形成器结构, 包含上下两条支路。其中上支路用于保证期望信号无损通过, 从而使下支路可以采用无约束自适应算法实现自适应权的迭代更新。通过设计上支路中的静态权向量W_q可以在保证信号不变的情况下, 实现低副瓣等波束方向图设计。

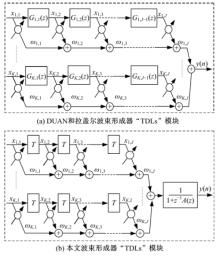
	Figure Option View Download New Window
	图1 GSC波束形成器结构Fig.1 Structure of GSC beamformer

T用于补偿非法线方向入射产生的时间延时。B是阻塞矩阵, 用于防止有效信号进入下支路。上支路中的“ TDL” 模块是为与下支路同步而引入的处理时延。下支路中的“ TDLs” 模块是GSC波束形成器的自适应模块, 用于实现干扰消除。传统时域宽带波束形成器的“ TDLs” 模块仅包含前向支路, 等效于在每个阵元后放置一个FIR滤波器。DUAN和拉盖尔波束形成器将“ TDLs” 模块中的TDL换成IIR滤波器, 引入反馈支路。图2(a)给出DUAN和拉盖尔波束形成器的“ TDLs” 模块。

	Figure Option View Download New Window
	图2 具有反馈支路的宽带波束形成器结构Fig.2 Structure of beamformer having feedback

二阶DUAN波束形成器的“ TDLs” 模块将原GSC的TDL替换成G_ij(z), 当a_ij_{, 2}为0时, 二阶DUAN波束形成器即变为一阶, 因而一阶可以看成是二阶波束形成器的特例, 即

$\begin{matrix} G_{ij} (z) = z^{- 1} / (1 - a_{ij, 1} z^{- 1} - a_{ij, 2} z^{- 2}) (1) \end{matrix}$

式中:a_ij_{, 1}和a_ij_{, 2}为第i个阵元的第j个抽头对应的IIR滤波器的反馈系数, 1≤ i≤ L-1, 1≤ j≤ M; L是接收阵列传感器个数, M是每个阵元后总的抽头个数。在DUAN波束形成器中, 反馈系数a_ij_{, 1}和a_ij_{, 2}也进行自适应更新。

拉盖尔波束形成器中, G_ij(z)具有如下形式:

$\begin{matrix} G_{ij} (z) = (z^{- 1} - b) / (1 - b z^{- 1}) (2) \end{matrix}$

式中:b是离线设计的最优极点。完整的拉盖尔波束形成器还需要在第一个抽头系数之前加上一个低通滤波器G_i₀(z)= $\begin{matrix} \sqrt[]{1 - b^{2}} \end{matrix}$ / $\begin{matrix} (1 - b z^{- 1}) \end{matrix}$ 。文献[12]基于Frost结构设计了拉盖尔波束形成器, 这种构建方法同样适用于GSC结构。本文为了尽可能地在相同条件下对比几种不同波束形成器的性能, 在仿真分析中, 采用的是基于GSC结构的拉盖尔波束形成器。

2 有固定反馈权的波束形成器设计

2.1 波束形成器结构

基于GSC结构的DUAN和拉盖尔波束形成器均采用相同的方式构建, 将原GSC波束形成器中的TDL换成各自对应的IIR滤波器。这种方式增加了自适应权更新的复杂性和运算量。

本文波束形成器的“ TDLs” 模块如图2(b)所示, 与DUAN和拉盖尔波束形成器构建方式不同的是:本文只增加了一条具有固定权的反馈支路, 前向支路保持不变, 且其余部分均与图1给出的GSC波束形成器相同。引入了反馈支路1/(1+z^-¹A(z)), 在每个阵元后形成了一个具有固定极点的IIR滤波器。其中, 反馈支路的分母部分1+z^-¹A(z)可以表示为:

$\begin{matrix} 1 + z^{- 1} A (z) = 1 + a_{1} z^{- 1} + a_{2} z^{- 2} + \dots + a_{M} z^{- M} (3) \end{matrix}$

2.2 前馈权的自适应更新算法

为了尽可能地消除干扰和噪声, 需要借助波束形成器的输出误差e(n)进行前向系数的自适应更新。

不失一般性, 本文采用最简单的静态加权和阻塞矩阵, 即静态加权W_q采用归一化均匀单位向量

$\begin{matrix} W_{q} = (1 / L) {[1, 1, \dots, 1]}^{T} (4) \end{matrix}$

阻塞矩阵B是一个L× (L-1)的矩阵, L是总的阵元个数, 表达式如下:

$\begin{matrix} B = (\begin{matrix} 1 & 0 & \dots & 0 \\ - 1 & 1 & \dots & 0 \\ 0 & - 1 & \dots & 0 \\ ︙ & ︙ & ︙ \\ 0 & 0 & \dots & - 1 \end{matrix}) (5) \end{matrix}$

假设图2(b)中每个阵元的相同抽头位置对应的输入信号组成向量为:

$\begin{matrix} x_{i} (n) = {[\begin{matrix} x_{1, i} (n) & x_{2, i} (n) & \dots & x_{L - 1, i} (n) \end{matrix}]}^{T} (6) \end{matrix}$

式中:i表示第i个抽头位置, 由图2(b)可得各抽头位置对应的输入向量满足以下关系:

$\begin{matrix} x_{i} (n) = x_{i - 1} (n - 1), i = 2, 3, \dots, J (7) \end{matrix}$

向量x_i(n)由式(6)给出, J表示TDL个数。由图1可得第一个抽头输入为:

$\begin{matrix} x_{1} (n) = B^{T} φ (n) (8) \end{matrix}$

向量φ (n)= $\begin{matrix} [φ_{1} (n), φ_{2} (n), \dots, φ_{L} (n)] \end{matrix}$ 是预延迟后的信号向量, L是总的阵元个数, 结合式(5)和(8), 得到x_j_{, 1}(n)=φ _j(n)-φ _j+₁(n), 其中j=1, 2, …, (L-1), 即第一个抽头对应输入的更新关系。式(7)和(8)构成了每次迭代下支路各抽头位置处信号向量的更新关系。

由图1可得波束形成器的输出误差为:

$\begin{matrix} \begin{matrix} e (n) = d (n) - y (n) = \\ d (n) - ω^{T} x (n) / (1 + z^{- 1} A (z)) = \\ d (n) - ω^{T} \bar{x} (n) (9) \end{matrix} \end{matrix}$

式中:x(n)是(L-1)× J维列向量, 由式(6)表示的x_i(n)按照i由小到大的顺序“ 拉直” 排列而成:

x(n)= $\begin{matrix} {[\begin{matrix} {x^{T}}_{1} (n) & {x^{T}}_{2} (n) & \dots & {x^{T}}_{J} (n) \end{matrix}]}^{T} \end{matrix}$ (10)

前向权向量采用同样方式构建, 有如下形式:

$\begin{matrix} ω = {[\begin{matrix} ω_{1, 1} & \dots & ω_{L - 1, 1} & \dots & ω_{1, J} & \dots & ω_{L - 1, J} \end{matrix}]}^{T} (11) \end{matrix}$

采用式(10)和(11)给出的信号和自适应权向量, 便可将全部自适应权看成一个整体, 以最小化式(9)表示的输出误差为准则进行自适应更新。ω ^Tx(n)构成了前向支路的输出, 考虑反馈支路, 需要构造含反馈的输入信号和输出信号, 用来实现自适应权的更新。

式(12)给出了含反馈的输入信号:

$\begin{matrix} \bar{x} (n) = x (n) / (1 + z^{- 1} A (z)) (12) \end{matrix}$

其单个元素的更新过程由式(13)给出:

$\begin{matrix} \begin{matrix} {\bar{x}}_{ij} (n) = x_{ij} (n) - a_{1} {\bar{x}}_{ij} (n - 1) - \\ a_{2} {\bar{x}}_{ij} (n - 2) - \dots - a_{M} {\bar{x}}_{ij} (n - M) (13) \end{matrix} \end{matrix}$

式中:a_i, 1≤ i≤ M表示第i个反馈权, M表示反馈权的个数。由此, ω ^T $\begin{matrix} \bar{x} \end{matrix}$ (n)才是整个波束形成器下支路的输出。

最优权向量的获取可以通过最小化均方误差‖ e(n)‖ ₂实现。该问题的目标函数表示为:

$\begin{matrix} \min_{ω} E {[e (n)]}^{2} (14) \end{matrix}$

这是一个无约束优化问题。定义代价函数为:

$\begin{matrix} η = E {[e (n)]}^{2} / 2 (15) \end{matrix}$

代价函数η 关于权ω 的导数为:

$\begin{matrix} \nabla_{ω} (n) = - e (n) \bar{x} (n) (16) \end{matrix}$

无约束RGN算法的权值更新过程为:

$\begin{matrix} ω (n) = ω (n - 1) - μ R_{\bar{x} \bar{x}}^{- 1} (n) \nabla_{ω} (n) (17) \end{matrix}$

式中:μ 是迭代步长; $\begin{matrix} R_{\bar{x} \bar{x}} \end{matrix}$ (n)是含反馈输入信号的相关矩阵, 通过如下迭代公式进行更新:

$\begin{matrix} R_{\bar{x} \bar{x}} (n) = (1 - μ) R_{\bar{x} \bar{x}} (n - 1) + μ \bar{x} (n) {\bar{x}}^{T} (n) (18) \end{matrix}$

利用矩阵求逆引理可得相关矩阵逆f(n)= $\begin{matrix} R_{\bar{x} \bar{x}}^{- 1} \end{matrix}$ (n)的迭代公式为:

$\begin{matrix} \begin{matrix} f (n) = \frac{1}{1 - μ} [f (n - 1) - \frac{μ}{β} Γ] (19) \\ 式中 : \\ β = 1 - μ + μ {\bar{x}}^{T} (n) f (n - 1) \bar{x} (n) \\ Γ = f (n - 1) \bar{x} (n) {\bar{x}}^{T} (n) f (n - 1) 。 \end{matrix} \end{matrix}$

基于以上分析, 用于自适应权ω (n)迭代更新的RGN算法流程如下(其中δ 是选定的一个正实数, δ I用来表示相关矩阵逆的初始估计):

(1)初始化:n=0, ω (0)=0, x(0)=0, f(0)=δ I。

(2)n=n+1, 利用式(7)(8)和(12)(13)计算x(n) and $\begin{matrix} \bar{x} \end{matrix}$ (n)。

(3)更新相关矩阵的逆:

f(n)= $\begin{matrix} \frac{1}{1 - μ} \end{matrix} \begin{matrix} [f (n - 1) - \end{matrix}$

$\begin{matrix} \frac{μ}{β} f (n - 1) \bar{x} (n) {\bar{x}}^{T} (n) f (n - 1)] \end{matrix}$ ,

其中, β =1-μ +μ $\begin{matrix} {\bar{x}}^{T} \end{matrix}$ (n)f(n-1) $\begin{matrix} \bar{x} \end{matrix}$ (n)。

(4)更新权值:

e(n)-d(n)-ω (n-1)^T $\begin{matrix} \bar{x} \end{matrix}$ (n),

$\begin{matrix} \nabla_{ω} \end{matrix}$ (n)=-e(n) $\begin{matrix} \bar{x} \end{matrix}$ (n),

ω (n)=ω (n-1)-μ $\begin{matrix} R_{\bar{x} \bar{x}}^{- 1} \end{matrix}$ (n) $\begin{matrix} \nabla_{ω} \end{matrix}$ (n)。

(5)重复步骤(2)~(4), 直至收敛或输入信号结束。

2.3 固定反馈权的离线设计

通过设计反馈权, 使反馈支路的频率响应逼近一个带通滤波器, 对于压制性干扰, 该带通滤波器尽可能覆盖接收机频带, 而对于欺骗性干扰, 该带通滤波器只需覆盖雷达信号频带。根据干扰的起止频率设计带通滤波器, 即可得到需要逼近的带通系统的冲激响应。将这一过程等效为用一个全极点系统逼近一个带通滤波器, 得到如下最小化问题:

$\begin{matrix} \min_{a} ‖ e ‖^{2} = \min \overset{N - 1}{\sum_{i = 0}} |h_{d} (i) - \frac{1}{D (z)} \{δ (i)\}| (20) \end{matrix}$

式中:e=h_d-h表示理想带通系统和实际全极点系统的单位冲激响应差, 理想带通系统的冲击响应为h_d=[h_d(0) h_d(1) … h_d(N-1)]^T, N是时域冲激响应的截断点数, h是由全极点系统表征的单位冲激响应, 表示如下:

$\begin{matrix} \begin{matrix} h = \frac{1}{D (z)} \{δ (i)\} = \\ {[\begin{matrix} h (0) & h (1) & \dots & h (N - 1) \end{matrix}]}^{T} (21) \end{matrix} \end{matrix}$

式中:D(z)=1+a₁z^-¹+a₂z^-²+…+a_Mz^-M, 全部反馈系数构成待优化向量a= $\begin{matrix} [\begin{matrix} a_{1} & a_{2} & \dots & a_{M} \end{matrix}] \end{matrix}$ 。最优反馈权向量a获取的迭代算法^[13]如下:

(1)初始化:n=0, a(0)=[1 ; -G^#g]^T, 其中, G^#=(G^TG)^-¹G^T表示G矩阵的广义逆。

(2)n=n+1, 重建A(n)矩阵, 计算

W(n-1)=A(n-1) $\begin{matrix} {(A^{T} (n - 1) A (n - 1))}^{- 1} \end{matrix}$ ,

X(n-1)=G^TW^T(n-1)W(n-1)=

G^T $\begin{matrix} {(A^{T} (n - 1) A (n - 1))}^{- 1} \end{matrix}$ 。

(3)更新反馈权向量:

a(n)=[1 ; -[X(n-1)G]^-¹X(n-1)g]^T; (4)终止条件判断:满足‖ e‖ ²≤ ε , 算法终止, ε 是预设误差容限; 否则, 跳转至步骤(2)。

对于上述迭代算法, 作如下说明:

(1)矩阵G是常量矩阵

向量g= $\begin{matrix} {[\begin{matrix} h_{d} (1) & h_{d} (2) & \dots & h_{d} (N - 1) \end{matrix}]}^{T} \end{matrix}$ , G和g都是由理想带通滤波器的单位冲激响应构成, 其中, N是冲激响应的长度, M是反馈权的个数。

(2)

A(n)是一个(N-1)× N的矩阵, 上述A(n)矩阵的每个元素都是关于迭代次数n的函数, 因而需要在每次迭代时都重新构建A(n)矩阵。

(3)上述迭代算法步骤(4)中给出的终止条件并不唯一, 实际中, 如果难以确定误差容限, 可以采用其他的终止条件, 如‖ e(n+1)-e(n)‖ ₂< ε , 表示目标函数值的变化非常小, 迭代算法达到稳态。

3 仿真实验与结果分析

本节采用均匀线阵仿真对比GSC、DUAN、拉盖尔和本文波束形成器的收敛速度、干扰抑制能力和运算量, 来体现本文波束形成器的优点和性能提升。并通过改变极点个数, 研究本文波束形成器干扰抑制能力的变化。最后, 仿真分析了本文波束形成器的稳定性。

3.1 SINR收敛曲线和干扰抑制能力分析

采用表1给出的仿真参数, 对每一种波束形成器实施1000次独立实验, 每次实验都进行800次迭代, 得到图3所示的800次迭代次数下的SINR收敛曲线, 图3是1000次独立实验的平均结果。

表1 仿真参数 Table 1 Simulation parameters

	Figure Option View Download New Window
	图3 SINR收敛曲线Fig.3 SINR convergence curves

从图3可以看出, 迭代次数为800时, 本文和GSC波束形成器都已平稳收敛, 且具有较好的稳态特性。而DUAN和拉盖尔波束形成器都呈现极缓的上升趋势, 未能完全收敛, 且DUAN波束形成器在第501次迭代时, 出现了明显的毛刺, 说明DUAN波束形成器存在不稳定的“ 隐患” 。

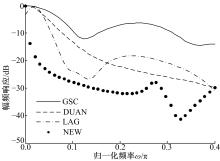
认为第800次迭代时, 各个波束形成器都达到稳定收敛状态, 取1000次独立实验中每次实验的第800次迭代结果计算阵列在干扰方向上的频率响应, 得到图4所示的干扰方向上阵列的频率响应曲线。

	Figure Option View Download New Window
	图4 干扰方向上波束形成器的频率响应Fig.4 Frequency response of four beamformers at direction of interference

图4进一步对比说明了4种波束形成器的干扰抑制能力, 可以看出本文设计的波束形成器, 在整个通带内的幅频响应都保持在最低状态, 因而具有最强的干扰抑制能力。这与图3得到的SINR收敛曲线的结果一致。

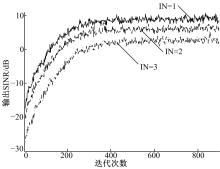
以上仿真实验均基于单个干扰, 下面讨论干扰个数对于本文波束形成器性能的影响。基于表1的仿真参数, 在其他仿真参数不变的情况下, 阵元通道数增加至5, 每个阵元后的抽头数为7, 将干扰个数从1增加至3, 分别采用本文构造的波束形成器进行500次独立实验, 得到图5所示的输出SINR收敛曲线。其中IN表示干扰个数, 可以看出随着干扰个数的增加, 收敛曲线的收敛速度降低。干扰个数依次递增时, 稳态达到的SINR分别为:8.947、6.159、3.225 dB。可见干扰个数增加时, 波束形成器的干扰抑制能力减弱并且收敛速度降低。

	Figure Option View Download New Window
	图5 不同干扰个数对应的SINR收敛曲线Fig.5 Convergence curves with variable interferences

值得说明的是, 上述干扰个数增加对波束形成器性能影响的结论同样适用于基于GSC结构的DUAN和拉盖尔波束形成器。为了在干扰个数增加的情况下仍然获得较强的干扰抑制能力, 需要增加权个数, 提高系统可用自由度。采用RGN迭代算法, 对于DUAN、拉盖尔和本文波束形成器, 每增加一个抽头系数, 单次迭代的平均运算增量(指乘法和加法的平均)分别为:1148、335和114。由此可以看出, 本文构造的波束形成器在应对多个干扰时具有一定的优势。

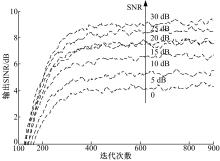
与传统GSC波束形成器相同, 输入SNR对波束形成器的干扰抑制能力有较大影响, 具体表现为, 输入SNR越大, 干扰抑制能力越强。为了验证输入SNR对于波束形成器性能的影响, 基于表1的仿真参数, 在其他仿真参数不变的情况下, 将输入信噪比从0以5 dB为间隔增加至30 dB, 分别基于本文构造的波束形成器进行500次独立实验, 得到图6所示的输出SINR收敛曲线。各种信噪比情况下稳态达到的SINR分别为:4.439、5.306、6.562、7.648、7.668、8.561、9.19 dB。

	Figure Option View Download New Window
	图6 不同输入SNR对应的SINR收敛曲线Fig.6 SINR convergence curves with variable input SNR

3.2 运算量的仿真与分析

由于本文设计的波束形成器只在全部前向支路求和后增加一条固定系数的反馈支路, 不同于DUAN和拉盖尔波束形成器, 将每个TDL均换成了相应的IIR滤波器, 因而本文波束形成器具有较低的运算量。

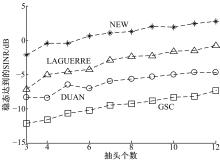
采用表1给定的仿真参数, 首先研究稳定收敛状态下SINR改善与抽头个数之间的关系, 将抽头个数从3增加至12, 观察1000次独立实验下, 每次独立实验第1000次迭代达到的SINR(仿真发现迭代次数为1000时, 所有波束形成器均已收敛)。图7给出了4种波束形成器的SINR关于抽头个数的变化曲线, 4条曲线给出的都是1000次独立实验的平均结果。

	Figure Option View Download New Window
	图7 SINR随抽头个数增加的改善Fig.7 SINR vs.number of taps

由图7可以看出, 本文波束形成器得到的SINR和抽头个数之间的关系曲线基本上与拉盖尔波束形成器的关系曲线平行, 平均SINR提升约为4.1319 dB, 相对于DUAN和GSC波束形成器提升分别为7.0806 dB和10.5208 dB。由图7可以看出, 为了实现相同的SINR改善, 例如期望SINR改善为17.805 dB时, 本文波束形成器只需要3个抽头, 拉盖尔波束形成器需要8个抽头, 而DUAN和传统的GSC波束形成器需要的抽头个数已经大于12个。由此可定性看出本文波束形成器的运算量相比于GSC、DUAN和拉盖尔波束形成器有所降低。

表2定量分析了实现17.805 dB的SINR改善时, 本文所述的4种波束形成器所需自适应权的个数和单次迭代下的运算量对比。可以看出实现相同的SINR改善, 拉盖尔波束形成器单次迭代的乘法和加法次数分别是本文波束形成器的6.8和5.9倍, 而GSC和DUAN波束形成器所需的运算量已远远大于本文波束形成器。

表2 4种波束形成器单次迭代的运算量分析 Table 2 Analysis of computational load in each iteration for four bemaformers

3.3 波束形成器干扰抑制能力与极点个数关系

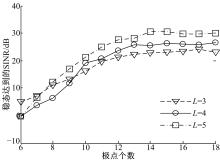
为研究本文波束形成器干扰抑制能力与反馈支路极点个数的关系, 分别对阵元个数为3、4和5的三种阵列进行仿真实验。基于表1给定的仿真参数, 对于每一种阵元数下的阵列, 将极点个数从6增加至18, 每次都进行500次独立实验, 每次独立实验包含1000次迭代。图8给出了每种阵元个数下得到的稳态SINR与极点个数之间的关系, 每条曲线都是500次独立实验的平均结果。

	Figure Option View Download New Window
	图8 稳态SINR与极点个数的关系Fig.8 SINR in steady-state vs.number of poles

由图8可以看出, 对于每种阵元数, 波束形成器稳态SINR都首先随着极点接近线性增长, 然后趋于饱和; 阵元个数越多, 饱和时所能实现的SINR改善也越好。稳态达到的SINR与反馈支路的极点个数之间的关系表明, 对于本文设计的波束形成器可以通过适当增加极点个数来获得更强的干扰抑制能力。

对于本文设计的波束形成器, 单次迭代, 乘法和加法次数的增量Δ _operand与极点个数的关系满足

$\begin{matrix} Δ_{operand} = (L - 1) \times J \times δ_{M} (22) \end{matrix}$

式中:L是阵元个数; J是抽头个数; δ _M是极点个数增量。对于阵元个数为4, 抽头数为3的情况, 达到饱和时的极点数为15, 收敛后最终SINR改善为34.84 dB。由表2可得, 极点个数为2时, SINR改善为17.805 dB。由式(22)得, 单次迭代的加法和乘法次数增量为117, 由表2可以看出, 此时本文波束形成器单次迭代的运算量仍远小于其他波束形成器, 但SINR提升了17.035 dB, 将近一倍。这说明, 本文波束形成器可以通过增加反馈支路的极点个数, 实现更强的干扰抑制。

3.4 本文波束形成器的稳定性说明

本文采用文献[13]给出的一种最优零极点系统识别方法离线获取最优极点。将全极点系统识别的非凸问题转化成迭代凸优化问题, 通过迭代优化得到全局最优解。为保证波束形成器的稳定收敛, 要求反馈支路的极点全部位于单位圆内。

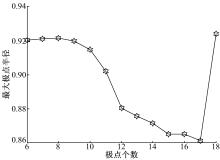
将极点个数由6增加至18个, 采用前馈权更新的RGN算法获取全极点反馈支路的反馈权。图9给出了不同极点个数下, 本文离线设计出的全极点反馈支路的最大极点半径。可以看出最大极点半径为0.924, 在单位圆内, 保证了本文设计的波束形成器的稳定性。

	Figure Option View Download New Window
	图9 不同极点个数下优化设计得到的最大极点半径Fig.9 Maximum pole radius with different number poles

4 结束语

针对现有含反馈支路的自适应宽带波束形成器运算量大、收敛慢和干扰抑制能力受限的问题, 设计了一种新的波束形成器。在传统GSC波束形成器的基础上, 增加一条具有固定系数的反馈支路, 离线确定最优极点位置, 在保证稳定性的前提下, 减少了所需自适应权的个数, 降低了运算量, 增强了干扰抑制能力。在相同仿真参数和自适应算法条件下, 仿真结果及分析表明本文波束形成器:①相比于拉盖尔、DUAN和GSC波束形成器平均SINR提升分别为4.1319、7.0806和10.5208 dB; ②实现相同SINR改善时, 相比于拉盖尔波束形成器, 单次迭代的乘法和加法次数分别降低了85.29%和83.5%, 且远小于DUAN和GSC波束形成器; ③增加极点个数, 可以以很小的运算增量换取较高的SINR改善; ④不同极点个数情况下, 反馈支路的最大极点半径始终小于1, 稳定性得到保证。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Melvin W, Scheer J. Principles of Modern Radar: Advanced Techniques[M]. Raleigh, NC: SciTech Publishing, Inc, 2013: 441-449. [本文引用:1]
[2]	Yan S, Sun H, Ma X, et al. Time-domain implementation of broadband beamformer in spherical harmonics domain[J]. IEEE Trans on Audio, Speech, and Language Processing, 2011, 19(5): 1221-1230. [本文引用:1]
[3]	Godara L C. Application of antenna arrays to mobile communications. II. beam-forming and direction-of-arrival considerations[C]∥Proc IEEE, New York, 1997: 1195-1245. [本文引用:1]
[4]	Frost III O L. An algorithm for linearly constrained adaptive array processing[C]∥Proc IEEE, New York, 1972: 926-935. [本文引用:1]
[5]	韦文, 李宁, 汤俊, 等. 基于分数时延的宽带自适应波束形成[J]. 清华大学学报: 自然科学版, 2011, 51(7): 988-992. Wei Wen, Li Ning, Tang Jun, et al. Broadband adaptive digital beamforming based on fractional delay[J]. Journal of Tsinghua University (Science and Technology Edition), 2011, 51(7): 988-992. [本文引用:1]
[6]	鄢社锋, 马晓川. 宽带波束形成器的设计与实现[J]. 声学学报, 2008, 33(4): 316-326. Yan She-feng, Ma Xiao-chuan. Designs and implementations of broadband beamformers[J]. Acta Acustica, 2008, 33(4): 316-326. [本文引用:2]
[7]	Griffiths L J, Jim C W. An alternative approach to linearly constrained adaptive beamforming[J]. IEEE Trans on Antennas and Propagation, 1982, 30(1): 27-34. [本文引用:1]
[8]	李涛, 李国林, 廖辉荣. 基于广义旁瓣相消器的滤波器组旁瓣干扰抑制[J]. 电子与信息学报, 2011, 33(1): 85-89. Li Tao, Li Guo-lin, Liao Hui-rong. Side-lobe interference suppression for filter banks based on GSC[J]. Journal of Electronics and Information Technology, 2011, 33(1): 85-89. [本文引用:1]
[9]	Vook F W, Compton R T Jr. Band width performance of linear adaptive arrays with tapped delay-line processing[J]. IEEE Trans on Aerospace and Electronic Systems, 1992, 28(2): 901-908. [本文引用:1]
[10]	Duan H P, Ng B P, See C M S. A new broadband beamformer using IIR filters[J]. IEEE Letters on Signal Processing, 2005, 12(11): 776-779. [本文引用:1]
[11]	Duan H P, Ng B P, See C M S, et al. Broadband beamforming using TDL-form IIR filters[J]. IEEE Trans on Signal Processing, 2007, 55(3): 990-1002. [本文引用:1]
[12]	Seydnejad S R, Ebrahimi R. Broadband beamforming using Laguerre filters[J]. Elsevier Journal on Signal Proc, 2012, 92(4): 1093-1100. [本文引用:1]
[13]	Shaw A. An optimal method for identification of pole-zero transfer functions[C]∥IEEE International Symposium on Circuits and Systems, NY, USA, 1992: 2409-2412. [本文引用:2]

2013

0.0

... 0 引言宽带波束形成器广泛应用于雷达^[1]、声呐^[2]和通信^[3]等技术领域 ...

2011

0.0

... 0 引言宽带波束形成器广泛应用于雷达^[1]、声呐^[2]和通信^[3]等技术领域 ...

1997

0.0

... 0 引言宽带波束形成器广泛应用于雷达^[1]、声呐^[2]和通信^[3]等技术领域 ...

1972

0.0

... Frost类^[4,5,6]和广义旁瓣相消(Generalized sidelobe canceller,GSC)类^[6,7,8]是两种传统的时域自适应宽带波束形成器结构 ...

2011

0.0

... Frost类^[4,5,6]和广义旁瓣相消(Generalized sidelobe canceller,GSC)类^[6,7,8]是两种传统的时域自适应宽带波束形成器结构 ...

2008

0.0

... Frost类^[4,5,6]和广义旁瓣相消(Generalized sidelobe canceller,GSC)类^[6,7,8]是两种传统的时域自适应宽带波束形成器结构 ...

1982

0.0

... Frost类^[4,5,6]和广义旁瓣相消(Generalized sidelobe canceller,GSC)类^[6,7,8]是两种传统的时域自适应宽带波束形成器结构 ...

2011

0.0

. 2011, 33(1):85-89 DOI:10.3724/SP.J.1146.2010.00280

Side-lobe interference suppression for filter banks based on GSC

基于广义旁瓣相消器的滤波器组旁瓣干扰抑制

Li Tao , Li Guo-lin , Liao Hui-rong.

李涛, 李国林, 廖辉荣

Naval Aeronautics and Astronautics University, Yantai 264001, China

In order to improve side-lobe performance, traditional filter banks have to increase order number. In this paper Generalized Side-Lobe Canceller (GSC) is introduced to cancel strong jamming signals from side-lobes of filter banks, which can place zeros at stop band adaptively. The matrix form of this adaptive algorithm is provided, based on LMS algorithm. The length of the canceller coefficients is confined so the canceller just cancels strong jamming signals, with little influence on pass band signals. This method realizes the function of high-order filter banks through low-order filter banks and especially suited for weak signal detection. The simulation analysis indicates that it reduces computation quantity relative to high-order filter banks but maintains the same performance.

传统滤波器组为降低旁瓣，需要提高滤波器阶数。该文将广义旁瓣相消的思想运用于滤波器组的旁瓣干扰抑制，在滤波器通带外的干扰信号频率处自适应形成零点。基于LMS算法，该文提出了基于自适应旁瓣相消器的滤波器组旁瓣干扰抑制算法，给出了算法的矩阵形式。通过限制系数长度，旁瓣相消器仅仅对消旁瓣大功率干扰信号，而对带内有用信号的影响很小，其作用相当于用一个低阶滤波器实现一个高阶数滤波器的功能，当信号功率较之干扰功率很小时尤其有用。仿真结果显示算法具有良好的旁瓣干扰抑制性能，较之高阶滤波器组大大减少了计算量。

... Frost类^[4,5,6]和广义旁瓣相消(Generalized sidelobe canceller,GSC)类^[6,7,8]是两种传统的时域自适应宽带波束形成器结构 ...

1992

0.0

... 由于只包含由抽头延迟线(Tapped delay line,TDL)组成的有限冲激响应(Finite impulse response,FIR)滤波器作为前向支路,随着信号带宽的增加,所需FIR滤波器的阶数,即TDL的数量也随之增加^[9],以获得预期的信号和干扰噪声比(Signal to interference pulse noise ratio,SINR) ...

2005

0.0

2007

0.0

2012

0.0

1992

0.0

... 为了简化权值迭代更新过程,加快收敛并增强波束形成器的干扰抑制能力,本文基于GSC波束形成器设计一种新的时域自适应宽带波束形成器,在保持前向支路不变的情况下,仅引入一条具有固定权值的反馈支路,采用一种最优迭代零极点系统识别方法^[13]离线获取最优反馈权 ...

... 最优反馈权向量a获取的迭代算法^[13]如下: ...