作者简介:郑欣(1981-),男,博士研究生.研究方向:数字图像处理、目标识别与跟踪.E-mail:zheng_xin2@sina.com
针对优度法在评价图像分割算法性能时忽略了图像质量对算法性能影响这一不足,分析了图像中影响分割算法性能的因素,并提出用图像活跃度定量描述上述因素。在此基础上,构造了一种基于图像质量的分割算法性能评价方法,即加权优度法。实验表明,加权优度法对分割结果的评价值与主观评价的一致性程度比优度法更高,评价结果与图像质量间的单调性也更好,证明了本文方法的有效性。
The excellent degree method is widely used in performance evaluation of image segmentation algorithms. However, this method ignores the influence of image quality. Hence, the results have no reference value to the overall performance evaluation of the segmentation algorithm or the comparison of different segmentation algorithms. To solve this problem, the image factors interfering with the performance of the segmentation algorithms were analyzed. Then, the metric Activity Degree of Image (ADI) was proposed to quantify these factors. Finally, based on the ADI, a performance evaluation method of the image segmentation algorithms was developed, named Weighted Excellent Degree (WED) method. Experiment results show that, compared with the current evaluation method, the WED method has higher consistency degree between evaluation results and subjective assessment, and better monotonicity between evaluation results and image qualities. Thus, the proposed WED method is more effective in performance evaluation of image segmentation algorithms than the current evaluation method.
图像分割是从图像处理进行到图像分析的重要环节。当前, Markov随机场[1]、模糊集[2]、分形[3]、水平集[4]、小波[5]、神经网络[6, 7]等理论均已被应用于分割算法的设计中。合理的算法性能评价方法不仅有助于分割算法的选择比较, 也能对分割算法的设计与发展起到指导作用。目前已经提出的分割算法性能评价方法可以分为主观评价法和客观评价法[8]。主观评价法无法定量评价分割结果[9], 评价过程受到人为主观因素干扰, 稳定性差, 评价效率低, 适用场合极其有限。客观评价法能定量测定图像分割的质量, 评价结果客观、稳定, 但由于忽略了图像质量对算法性能的影响, 仅对分割后的结果图像进行分析, 其评价结果在某些场景下与实际情况并不符合。
本文针对上述问题, 首先对现有分割算法评价方法的不足进行了总结, 接着分析了图像中影响分割算法性能的因素, 并提出了图像质量描述指标图像活跃度(ADI), 以对图像中影响分割算法性能的因素进行定量描述。在此基础上, 提出一种基于图像质量的分割算法性能评价方法, 从而有效地解决了现有评价方法忽略了图像质量对分割算法性能干扰的不足。
分割算法的客观评价方法, 根据其工作原理可分为两种:①差异法, 即有监督的评价方法。差异法通过比较分割结果和标准图像之间的异同, 能对算法性能进行较为准确、可靠的评价。差异法的实现必须以获得标准图像为前提, 但获取标准图像往往并不容易[10, 11], 因而, 其适用范围受到很大的限制; ②优度法, 即无监督的评价方法, 利用一组参数测度对分割结果进行定量评价, 并且在评价过程中不需要获取标准图像[10, 11]。优度法中所使用的参数测度, 要求符合观察者的主观感知, 并与图像分割定义一致, 常用测度包括:区域一致性RU[7](Region uniformity)、区域对比度RC[12](Region contrast)、区域形状测度RSM[7](Region shape measure)、综合指标CI[13](Composite indicator)等, 上述指标分别如式(1)~式(4)所示。
式中:RU反映了区域内部的灰度一致性, 其中A为图像像素数, 区域i的灰度方差为
式中:RC反映了前景与背景的差异程度, 其中前景灰度均值为fo, 背景灰度均值为fb, RC取值范围为[0, 1], 值越大代表分割效果越好。
式中:RSM反映了各区域的边缘平滑程度。邻域N(x, y)的灰度均值为fN(x, y), 灰度阈值为t, 广义梯度为Δ (x, y), 归一化因子为C, sgn(x)为符号函数。RSM取值范围为[0, 1], 值越大代表分割效果越好。
上述指标分别从不同的角度描述了分割算法的性能, 因此, 仅使用单独一个指标不能够全面、准确地反映分割算法的性能。为了解决该问题, 将上述3个指标进行融合, 融合后的指标称为综合指标CI, 如式(4)所示, 其取值范围为[0, 1], 值越大表明分割效果越好。
优度法摆脱了对标准图像的依赖, 因而得到广泛应用[11]。然而进一步的研究发现, 优度法仅分析了分割后的结果图像, 未考虑输入图像质量的影响。对图像分割算法进行测试时发现, 同一分割算法在不同图像上的表现并不一致, 而各类分割算法由于原理不同, 在不同输入图像条件下的分割性能也各有优劣。譬如, 对于简单的图像, 两个不同的分割算法均能很好地分割出前景与背景区域, 但是对于复杂的输入图像, 不同算法的分割效果就有了很大差异。这表明输入图像的质量将对分割算法的性能产生很大的影响。因此, 优度法抛开图像质量的影响, 仅分析了分割结果图像, 其评价结果显然是不完善的。这样虽然能够从度量参数的绝对数值上看出算法对特定图像的分割效果, 但是对于其他图像, 该结果将失去参考价值, 并且由此得到的结论对于算法的整体性能评价和不同算法间的比较选择的意义并不大。
因此, 有必要提出一种新的、有效的分割算法性能评价方法。在提出新的评价方法之前, 首先分析了图像中影响分割算法性能的因素, 进而从图像分割难易程度的角度出发, 提出用于描述图像质量的指标, 即图像活跃度。在此基础上, 提出一种基于输入图像质量的分割算法性能评价方法。
虽然不同分割算法的理论依据、构造方式有所不同, 但影响图像分割结果的方式相同, 即发生过分割或欠分割。进一步研究发现, 过分割或欠分割是由图像中不同区域的复杂程度造成。以图1为例进行说明, 图1(a)(b)为同一幅图像, 在图1(b)中用编号、方框标识图像的不同区域。对比图1(b)中6个区域可知, 区域间的复杂程度差异较大。采用不同算法对图1(a)进行分割, 包括Ostu方法、脉冲耦合神经网络方法、Markov随机场方法, 均出现了部分简单区域过分割和部分复杂区域欠分割。
由上述分析可知:图像中不同区域的复杂程度将对分割性能造成影响, 复杂程度越大, 则影响越大。而如何划分图像中复杂程度不同的区域, 是在提出对图像复杂程度的定量描述方法之前需要解决的问题。
文献[6]提出一种图像区域自适应划分及量化区域复杂程度的方法:将图像M× N等分, 若子区域均方差均小于K× MSE, 表明图像内部复杂程度相近, 则取消分块。当某个子区域均方差大于L× MSE时, 表明该区域内部复杂程度相差较大, 对其继续等分, 直到均方差小于L× MSE或子区域的长、宽小于规定值。MSE为整幅图像的均方差, 调节系数L> K≥ 1.0。此时, 图像分为内部复杂程度相近的区域, 再采用式(5)所示的局部图像活跃度ADLA[6](Activity degree of local area)量化各区域的复杂程度。
式中:BE为区域图像灰度共生矩阵的信息熵; MAX(BE)为区域图像灰度共生矩阵在理论上的最大信息熵。ADLA体现了局部区域图像的复杂程度, 取值范围为[0, 1], 值越大, 该区域图像的复杂程度越高, 其计算过程较为复杂, 技术细节可参见文献[6]。计算了图1(b)中不同区域的ADLA指标:区域1为0.760; 区域2为0.797; 区域3为0.671; 区域4为0.598; 区域5为0.434; 区域6为0.208。上述结果表明, 区域6、5、4、3、1、2的复杂程度依次增大。观察图1(b)可知, 该评价结果符合实际情况。
在对图像区域自适应划分并量化描述各区域复杂程度的基础上, 提出“ 图像活跃度” 的概念, 用于描述在图像中进行分割的难易程度, 2.3节给出了该指标的详细定义以及计算方法。
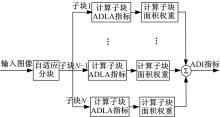
图像活跃度ADI(Activity degree of image)体现了一幅图像的复杂程度, 其取值范围为[0, 1], 值越大, 表明图像复杂程度越大。当一幅图像中不同区域内的像素出现概率相同、空间均匀分布时, 取得最大值1。由2.1节可知, ADI受到两个因素影响:①子块图像的复杂程度越大, 该子块权重越大; ②子块图像的面积越大, 该子块权重越大。因此, 计算ADI指标时, 首先通过自适应分块, 对图像不同区域进行划分; 然后, 计算各子块的ADLA指标; 最后, 计算各子块的面积权重。算法细节如图2所示, 文字表述如下:
步骤1:采用2.2节的自适应分块策略, 对图像中的不同区域进行划分。
步骤2:根据式(5), 计算各子块图像的局部图像活跃度ADLAi。
步骤3:根据式(6)计算各子块图像的面积权重, 其中wi表示第i个子块图像的面积权重, A为整幅图像的面积, Ai为第i个子块图像的面积。
步骤4:计算图像的ADI指标, 如式(7)所示:
ADI指标可以准确地描述图像的复杂程度, 这是下一步进行图像分割算法性能评价的基础。
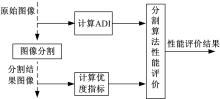
基于图像质量描述指标ADI, 提出一种新的分割算法性能评价方法, 其流程如图3所示:即通过ADI指标、优度指标分别描述输入图像质量、分割后结果图像的优度度量, 在此基础上, 构造了量化描述图像分割算法性能的评价方法, 即加权优度法, 其定义如式(8)所示:
式中:N为图像子块数; WEDi为子块i的加权优度指标。根据第2节的分析, WEDi受两个因素影响:①子块图像的复杂程度越大, 其值越大; ②子块图像的面积越大, 其值越大。因此, WEDi的计算如式(9)所示:
式中:Ai为第i个子块的面积; ADLAi为局部活跃度指标; EDi为第i个子块分割结果的优度指标。
根据加权优度法的定义, 当式(9)中EDi分别采用指标RU、RC、RSM时, 将得到3个加权优度指标, 即:加权区域一致性测度WRU(Weighted region uniformity)、加权区域对比度WRC(Weighted region contrast)、加权区域形状测度WRSM(Weighted region shape measure)。WRM、WRC、WRSM的取值范围均为[0, 1], 值越大意味着分割效果越好。将上述3个加权指标进行融合, 融合后的指标称为加权综合指标WCI(Weighted composite indicator)。实验中, 采用了简单的融合方法, 如式(10)所示:
式中:WCI取值范围为[0, 1], 值越大表明分割效果越好。
为验证本文分割算法性能评价方法的有效性, 利用50幅256× 256像素的图像进行了实例验证:首先计算图像的ADI指标(图像分块时, 系数K取1.2, L取1.5, 子块长、宽最小32像素)。然后分别采用优度法、本文方法对每幅图像的不同分割结果进行评价并排序。由于实验数据较多, 仅以图4(a)~(d)所示4幅具有代表性的图像为例进行详细说明。图4(a)(b)(c)(d)的ADI指标计算结果分别为0.163、0.318、0.645、0.813, 优度法(CI指标)评价及排序结果如表1所示, 本文方法(WCI指标)评价及排序结果如表2所示。最后以关系图的形式, 分别给出了利用优度法、本文方法针对50幅图像的最佳分割结果的评价值与图像质量指标ADI的关系, 如图5所示。
(1)图像分割算法
所有分割结果均通过Stewart PCNN模型分割得到[14]。采用该方法进行图像分割时, 通过调整模型中的耦合系数即可调节算法的分辨率, 较小的耦合系数表征该模型分割图像时具有较高分辨率[14]。通过选取耦合系数, 为每幅图像提供了4个不同的分割结果, 其中包括1个分割适中的结果, 还有1~2个过分割的结果、1~2个欠分割的结果, 选择上述分割结果有助于直接从视觉上对它们进行排序。
(2)实验数据说明
图4所示为4幅典型图像及其不同的分割结果, 为了判断评价方法对这些分割结果评判的有效性, 提前对不同的分割结果进行人为排序。在每行中, 从左至右, 第1幅图像为原始图像, 后续的图像为分割结果, 以#号开头的编号就是对这些分割结果的人为排序。
由ADI指标计算结果可知:图4(a)的复杂程度最低(ADI为0.163), 图4(b)和(c)的复杂程度依次增大(ADI分别为0.318、0.645), 图4(d)的复杂程度最大(ADI为0.813)。观察图4可知:图4(a)的纹理简单, 场景复杂程度在4幅图像中最低; 图4(b)左上方区域的纹理复杂程度较高, 其他区域的纹理简单, 该图的场景复杂程度高于图4(a); 图4(c)上方区域的纹理复杂, 但下方区域的纹理简单, 该图的场景复杂程度高于图4(b); 图4(d)中, 整幅图像纹理复杂, 场景复杂程度在4幅图像中最高。
上述结果表明, ADI指标度量结果符合实际情况, 对于评定图像的复杂程度是有效的, 能准确反映出图像质量对分割算法性能的影响程度。
表1、表2分别记录了图4中4幅图像不同分割结果所对应的CI、WCI指标的计算结果(括号外)以及排序(括号内)。由图4可以看出, 分割结果的人为排序在视觉感官上是合理的。根据表1中的数据可知, 指标CI给出的排序结果出现了与人为排序结果不一致的情况, 如图4(b)、图4(d)分割结果的评价排序。根据表2可知, 指标WCI给出的排序结果与人为排序结果完全一致。
| 表1 CI指标评价结果及排序 Table 1 Evaluation results of four images using metric CI and their sorted result |
| 表2 WCI指标评价结果及排序 Table 2 Evaluation results of four images using metric WCI and their sorted result |
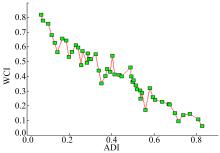
图像分割算法的性能与图像质量紧密相关, 有效的算法评价指标与图像质量之间应按概率呈现单调关系[15, 16]。为了进一步验证本文评价方法的有效性, 在上述实验条件下(分割算法相同, 图像样本相同), 分析了分割算法性能评价指标CI、WCI与图像质量描述指标ADI的关系。图5、图6反映了50幅图像的最佳分割结果的评价值与图像质量描述指标的关系。图5所示结果表明, CI与图像质量的相关性较低, 而图6的结果则表明WCI与图像质量之间呈现出较好的单调关系, 具有很强的相关性。上述实验结果进一步表明了本文方法优于优度法。
相比于优度法, 本文方法的优势具体体现在以下3个方面:
首先, 本文提出的评价方法, 考虑了图像质量对分割算法性能的影响。优度法忽略了图像质量对分割算法性能的影响, 评价分割结果时, 对所有区域采用相同权值, 从而导致在某些情况下, 评价结果与实际情况不符。本文方法根据区域的图像质量, 对不同区域的分割结果进行加权, 克服了优度法的上述缺陷。4.2节的实验表明, 本文方法与分割算法的实际性能更加吻合, 更适合于分割算法性能的评价。
其次, 实现了分割算法对不同图像上分割效果的评价。优度法缺少对输入图像质量的对比, 从而很难对分割算法在不同图像上的分割效果进行对比。本文方法通过ADI指标量化输入图像的质量, 并通过加权优度指标对分割算法的性能进行评价, 克服了优度法的上述不足。
最后, 本文方法用于评价图像分割算法的性能时, 提供了更有意义、更直观的信息。进行分割算法性能评价时, 一些研究者仅关注不同分割算法作用于同一幅图像时的性能, 另一些研究者则关注同一分割算法作用于不同图像时的性能。在本文方法中, 这些不同的需求均能满足:①图像质量指标ADI, 以及算法性能指标WCI均采用归一化的形式, 取值范围均为[0, 1], 便于量化比较不同图像的质量, 以及不同分割算法的性能; ②通过比较新指标的实际值与理想值1, 可以直观地体现出特定分割算法的性能。
理论分析与实验表明, 相比于优度法, 本文方法的评价结果更为有效, 与主观评价的一致性程度更高, 从而有效地解决了现有评价方法忽略了图像质量对分割算法性能影响的不足。此外, 本文方法还能提供图像质量对分割算法性能影响的信息。虽然实验表明本文方法优于优度法, 但还不能将本文方法当作对图像分割评价的一个完善的标准评价方法, 需要进行更多的对比实验, 例如采用更多的分割算法, 对更多的分割结果进行分析, 这是有待进一步研究的课题。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|