面向H.264的多级自适应快速整像素运动估计算法

引用本文

姚睿, 郭庆新, 孙艳梅, 何坤, 张砦. 面向H.264的多级自适应快速整像素运动估计算法. 吉林大学学报: 工学版, 2016, 46(1): 318-326
YAO Rui, GUO Qing-xin, SUN Yan-mei, HE Kun, ZHANG Zhai. Multi-level adaptive fast integer pixel motion estimation algorithm for H. 264. Journal of Jilin University Engineering and Technology Edition, 2016, 46(1): 318-326 复制到剪切板

Permissions

面向H.264的多级自适应快速整像素运动估计算法

姚睿, 郭庆新, 孙艳梅, 何坤, 张砦

南京航空航天大学自动化学院,南京 210016

作者简介:姚睿(1974-),女,副教授,博士.研究方向:DSP理论与技术,演化硬件理论与技术,嵌入式测控系统,智能电路.E-mail:yaorui@nuaa.edu.cn

基金:国家自然科学基金项目(61202001,60871009); 中央高校基本科研业务费专项项目(NS2014036)

摘要

为了减少运动估计计算量,提高视频编码效率,提出了一种多级自适应快速整像素运动估计算法。首先,根据前一帧的帧级运动强度和当前块预测运动矢量(PMV)分别预测帧级和宏块级搜索范围,取其中最小值作为最终搜索范围。其次,根据宏块级运动强度,将宏块分为低、中、高三种运动强度类型,针对不同的类型自适应选择钻石、改进的六边形、UMHexagonS算法模板。然后,根据宏块运动矢量方向性,对高运动强度类型宏块采取方向自适应搜索策略。最后,对UMHexagonS算法进行了改进。实验结果表明,本文算法比FFS、UMHexagonS、EPZS算法分别平均减少了70.290%、19.124%、14.113%的运动估计时间,而峰值信噪比基本不变且码率增加较少。

关键词: 信息处理技术; 快速整像素运动估计; 运动强度; 自适应; UMHexagonS

中图分类号:TN91 文献标志码:A 文章编号:1671-5497(2016)01-0318-09

Multi-level adaptive fast integer pixel motion estimation algorithm for H. 264

YAO Rui, GUO Qing-xin, SUN Yan-mei, HE Kun, ZHANG Zhai

College of Automation Engineering, Nanjing University of Aeronautics and Astronautics,Nanjing 210016, China

Abstract

In order to reduce the complexity of motion estimation and improve the efficiency of the video encoder, a novel multi-level adaptive fast integer pixel motion estimation algorithm is proposed. First, based on the frame-level motion intensity of previous frame and the predictive motion vector of current block, the frame-level search range and macroblock-level search range are predicted, and the smaller range is taken as the final search range. Second, the macroblock is divided into low, medium and high motion types according to the macroblock-level motion intensity; the Diamond, Hexagon improved or UMHexagonS improved algorithmic templates are adaptively selected. Then adaptive motion estimation of the high motion type macroblock is taken in a certain direction based on the directivity of the motion vector. Finally, improvements are made on the inefficient parts of the UMHexagonS algorithm. Experiment results show that, compared with the full search algorithm, UMHexagonS algorithm and EPZS algorithm, the proposed algorithm can averagely reduce the estimation time by 70.29%, 19.12% and 14.11% respectively, while, the Peak Signal to Noise Ratio (PSNR) and bit rate remain almost unchanged.

Keyword: information processing; fast integer pixel motion estimation; motion intensity; adaptive; UMHexagonS

Show Figures

0 引言

运动估计作为视频编码的核心技术, 能有效去除图像序列的帧间冗余, 从而实现高效编码。H.264中, 运动估计采用先进的可变尺寸块和多参考帧技术, 需要对每一参考帧中预定搜索范围内所有块进行匹配, 寻找最优解。因此, 其高质量的编码效果是以巨大的计算复杂度为代价获取的。研究表明, H.264中, 运动估计时间占整个编码过程的60%~80%^[1], 因此研究快速有效的运动估计算法一直是视频编码领域的热点问题。

运动估计算法中搜索精度最高的是全搜索算法, 但其计算量较大, 效率较低。因此各国学者提出了许多快速算法以减少计算量^{[2, 3, 4]}, 包括三步法(TSS)、新三步法(NTSS)、四步法(FSS)、钻石法(DS)以及基于六边形的搜索法(HEXBS)^[5]等。上述均采用一定的搜索模板, 根据运动矢量的中心偏置分布特性^[6], 逐步更新下一步搜索方向和模板中心。这些算法在很大程度上降低了计算复杂度, 但是并没有从全局上考虑运动方向以及运动矢量的相关性^[7], 容易陷入局部最优点, 导致率失真性能降低, 影响运动估计效果。为了提升编码性能, 后来提出的EPZS算法^[8]、UMHexagonS算法^[9]等混合了多种技术, 如起始搜索点预测、提前终止策略以及混合模板等。这些算法大大提高了编码性能, 如UMHexagonS算法可在比FS算法节省约90%计算量的情况下, 得到非常接近FS算法的运动估计效果, 并能适应于各种运动类型的视频序列。然而, 该算法依然存在以下问题:第一, 对不同运动程度块的搜索范围固定, 运动估计过程中可能存在因搜索范围过大引起的不必要搜索和搜索范围过小导致搜索不完整的现象, 从而影响编码性能; 第二, 对同一帧中所有宏块采用固定模板, 搜索效率较低; 第三, 没有利用运动矢量的方向性^[10], 搜索过程中会进行不必要的搜索, 影响搜索速度。

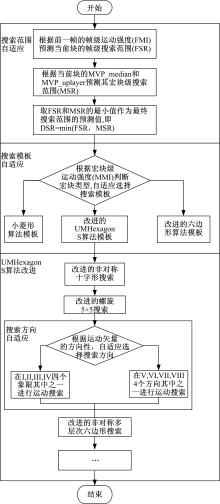
针对上述问题, 本文提出了多级自适应运动估计算法(MA_DHUS)。该算法首先利用搜索范围动态调整技术, 解决搜索范围过大和过小问题:动态判决帧级搜索范围和宏块级搜索范围, 取两者中较小者作为运动估计搜索范围。然后根据宏块运动程度的不同选择不同的搜索模板, 以提高搜索效率:根据宏块级运动强度将宏块分为低、中、高三类强度, 并对这三种强度宏块分别选择钻石算法模板、改进六边形算法模板和改进的UMHexagonS算法模板。其中, 在UMHexagon算法改进部分加入了搜索方向自适应技术, 明显减少了搜索点数, 同时又对非对称十字形和非对称多层次六边形等进行了改进。该算法能在码率增加很小并保证图像质量的情况下, 节省运动估计时间, 提高编码效率。

1 视频运动强度的描述

1.1 帧级运动强度的引入

观察视频序列会发现, 当场景无突变时, 其运动是一个缓慢变化的过程, 且各种视频序列的运动有强有弱, 变化程度不尽相同。故可通过识别帧间图像的运动程度, 依据运动相关性, 用当前帧的运动情况预测下一帧的运动情况。在MPEG-7标准中提出了运动活性(Motion activity), 它用来描述视频中镜头移动的剧烈程度。然而, 其运动活性是按镜头提取的, 由于实际视频中视频镜头非常短, 故运动活力无法很好地描述视频中每帧图像运动的剧烈程度^[11]。为此, 本文定义帧级运动强度(Frame motion intensity)的概念, 描述每帧图像的运动程度, 并借鉴运动活性^{[11, 12]}的计算方法进行分析。

定义1 视频帧级运动强度:提取视频中每帧编码P帧的运动矢量进行计算, 将用于描述每一帧相对于上一帧运动剧烈程度的量化数值称为帧级运动强度, 其计算方法如下:

(1)提取视频中每帧编码P帧中每个4× 4块的运动矢量, 定义其幅度矩阵C_mv。C_mv是I× J阶矩阵, I、J分别代表一个P帧中x和y方向上的4× 4块的数目。矩阵元素C_mv(i, j)描述了P帧(i, j)块处的运动幅度, 其计算方法如下:

$\begin{matrix} C_{mv} (i, j) = \sqrt[]{x_{i}^{2} + y_{j}^{2}} (1) \end{matrix}$

式中:x_i和y_j分别表示(i, j)块在x和y方向上的运动矢量。

(2)计算每一P帧中所有4× 4块的平均运动幅度 $\begin{matrix} C_{mv}^{avg} \end{matrix}$ 。

$\begin{matrix} C_{mv}^{avg} = \frac{1}{IJ} \overset{I}{\sum_{i = 1}} \overset{J}{\sum_{j = 1}} C_{mv} (i, j) (2) \end{matrix}$

(3)计算该P帧运动幅度的标准差FMI。

$\begin{matrix} FMI = \sqrt[]{\frac{1}{IJ} \overset{I}{\sum_{i = 1}} \overset{J}{\sum_{j = 1}} (C_{mv}^{avg} - C_{mv} {(i, j))}^{2}} (3) \end{matrix}$

将FMI值进行量化即可得到每帧的帧级运动强度信息。结合对标准测试序列中典型片段的分析发现, 运动估计搜索范围大小与帧级运动强度存在着密切的联系:帧级运动强度越剧烈, 运动估计搜索范围越大; 反之则越小。依据相邻帧间运动的相关性, 通过当前帧的帧级运动强度信息预测下一帧运动估计的搜索范围是一种有效降低运动估计计算量的方式。

1.2 宏块级运动强度的引入

每帧图像中, 所有宏块的运动程度并不一致, 大部分宏块处于低速运动状态, 即使在运动剧烈的视频序列中, 处于高速运动的宏块也占少数。为表征宏块的运动程度, 本文提出了宏块级运动强度(Macroblock motion intensity)概念。

定义2 宏块级运动强度:取当前块运动矢量的中值预测值(MVP_median)、上层块预测值(MVP_uplayer)、相邻参考帧预测值(MVP_nrp)三个运动矢量横纵坐标分量的最大值, 作为宏块级运动强度。计算方法如下:

$\begin{matrix} \begin{matrix} MMI = \max (\max (MVP_median_x, \\ MVP_uplayer_x, MVP_nrp_x), \\ \max (MVP_median_y, \\ MVP_uplayer_y, MVP_nrp_y)) (4) \end{matrix} \end{matrix}$

经过对标准序列中典型片段的分析发现, 宏块的最终运动矢量与宏块级运动强度存在着紧密的联系:宏块级运动强度越大, 运动矢量越大, 即最佳匹配点距搜索起始点越远; 反之, 运动矢量越小, 最佳匹配点距搜索起始点越近。因此, 可以根据最佳匹配点距搜索起始点的远近选择适合的算法模板进行运动搜索, 以避免搜索不完全和搜索过剩的情况, 从而提升搜索速度和搜索精度。

2 多级自适应运动估计算法(MA_DHUS)

2.1 自适应搜索范围的引入

视频中物体的运动程度并不相同:对于快速运动的情况, 需要进行大范围运动搜索找到最优匹配位置; 而对于低速运动的情况, 最优匹配位置一般不会偏离搜索起点太远。现有的搜索范围控制算法一般是基于块级别的, 虽然基于块的搜索范围调整能够较精确地确定运动信息, 但是当前宏块与周围宏块之间会产生处理上的相关性。为了获得更好的效果, 本文采取帧级预测和宏块级预测相结合的方法调整运动估计搜索范围。

2.1.1 帧级搜索范围预测(FSR)

通过对标准视频序列帧级运动强度和运动矢量分布的分析发现, 两者之间大体满足如下规律:

当FMI< 30时, 帧内宏块的运动向量绝大多数在± 8范围内; 当30≤ FMI< 50时, 帧内宏块的运动向量绝大多数在± 12范围内; 当FMI≥ 50时, 帧内宏块的运动向量绝大多数在± 16范围内。

由此, 可以根据当前帧帧级运动强度预测下一帧运动估计的帧级搜索范围(FSR):①若FMI< 30, FSR=± 8; ②若30≤ FMI< 50, FSR=± 16; ③其他, FSR=± 12。

2.1.2 宏块级搜索范围预测(MSR)

宏块级搜索范围预测(MSR)是指根据当前块的尺寸动态调整搜索范围。MSR的大小借鉴文献[13]中动态搜索窗计算方法, 根据运动矢量的中值预测值(MVP_median)和上层预测值(MVP_uplayer)计算。

最终, 在得到FSR预测值和MSR预测值后, 取其中最小值作为动态搜索范围(DSR)的大小, 即:

$\begin{matrix} DSR = \min (FSR, MSR) (5) \end{matrix}$

2.2 自适应模板搜索模式

利用宏块级运动强度MMI判断宏块的运动类型, 设置运动类型判别阈值L₁和L₂以对运动类型进行分类, 且L₁≤ L₂。对不同类型的宏块采取不同的搜索算法, 具体如下:①若MMI< L₁, 为缓慢运动块, 采用钻石搜索; ②若MMI≥ L₂, 为剧烈运动块, 采用改进的UMHexagonS算法模板搜索; ③其他, 为中等运动块, 采用改进的六边形模板搜索。

在实际视频编码中, 阈值L₁和L₂的取值可根据视频序列的类型和编码器端的需要灵活设定。若设定L₁=L₂=0, 帧内所有宏块均为剧烈运动块; 若设定L₁=L₂=max, 则所有宏块均为缓慢运动块。

通过实验数据统计, 对于一般的视频序列, 当L₁=2, L₂=4时最能表征宏块的运动类型, 因此本文设定运动类型判定阈值为L₁=2, L₂=4。

2.3 改进的六边形搜索模式

传统的六边形搜索算法未采用起始搜索点预测技术, 而是以当前编码块的位置作为搜索中心点, 导致搜索点过多, 影响编码效率。为减少计算量, 并能较快搜索到最优点。本文针对六边形算法, 引入最优点预测搜索, 包括中值预测、原点预测、上层预测以及多参考帧预测4种起始点预测方案; 并加入小菱形搜索以更快地搜索到最优预测起始点。

2.3.1 最优点匹配准则

在选择最优点时, 采用绝对误差和(SAD)作为匹配准则, 如式(6)所示:

$\begin{matrix} \begin{matrix} SAD (i, j) = \\ \overset{M}{\sum_{m = 1}} \overset{N}{\sum_{n = 1}} |f_{k} (m, n) - f_{k - 1} (m + i, n + j)| (6) \end{matrix} \end{matrix}$

式中:(i, j)为运动矢量; f_k、f_k-₁分别为当前帧和上一帧的像素值; M、N分别为块的宽和高的像素个数; m、n分别为块内像素点的横、纵坐标。当SAD(i, j)为最小时, 当前块为最佳匹配块。

2.3.2 预测流程

加入起始搜索点预测后的预测流程如下:

(1)将中值预测得到的预测点作为搜索点, 计算SAD值, 保存为当前最优点。

(2)以中值预测点作为中心点进行小菱形搜索, 计算并比较SAD值, 将SAD值最小的点更新为最优点。

(3)计算原点预测点SAD值, 比较SAD值, 并更新最优点。

(4)若原点为最优点, 则以原点为中心进行小菱形搜索, 计算并比较SAD值并更新最优点, 转到步骤(5); 否则, 最优点为中值预测点或其周围4个点, 直接转到步骤(5)。

(5)进行上层预测和多参考帧预测, 计算并比较SAD值并更新最优点。

(6)以以上步骤的最优点作为中心进行小菱形搜索, 计算并比较SAD值, 更新最优点。

(7)将得到的最优点作为预测起始点进行六边形搜索。

2.3.3 六边形内部搜索模式改进

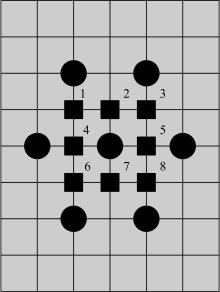
原六边形算法最后一步采用了菱形搜索算法, 如图1所示, 当六边形搜索得到的最优点位于六边形中心时, 接下来会检查2、4、5、7四个点, 这样就漏掉了1、3、6、8点的检测, 导致搜索精度不高。本文采用文献[14]的计算方法使得内部点搜索只需要搜索一个特定方向即可, 在搜索速度和失真的表现上优于传统六边形搜索模式。

	Figure Option View Download New Window
	图1 六边形内部点分布Fig.1 Distribution of hexagon inner points

2.4 UMHexagonS算法的改进

2.4.1 UMHexagonS算法简介

UMHexagonS算法包含了以下3个部分。

(1)精准的起始搜索点预测。分别采用原点预测、中值预测、上层预测和多参考帧预测4种起始点预测模式, 计算代价并取最小代价处的点作为最优起始搜索点。

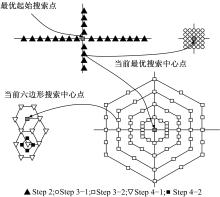
(2)混合搜索模板的使用。包含5种搜索模式:即非对称十字形搜索、螺旋5× 5全搜索、非均匀多层次六边形格点搜索、六边形搜索、小菱形搜索。算法流程如图2所示。

	Figure Option View Download New Window
	图2 UMHexagonS算法搜索流程Fig.2 Search process of UMHexagonS

(3)采用了提前终止策略。UMHexagonS算法在检测上层块MV、起始搜索点确定、各模板检测等多处进行提前终止检测, 对满足条件的可跳过部分搜索模板, 直接进行后面的模板搜索。

尽管UMHexagonS算法效果相当好, 但是在搜索过程中仍然存在搜索点过多的情况, 因此该算法仍然有待改进。本文通过对UMHexagonS算法的研究, 又在如下几方面对其进行了改进。

2.4.2 非对称十字形和多层次六边形的改进

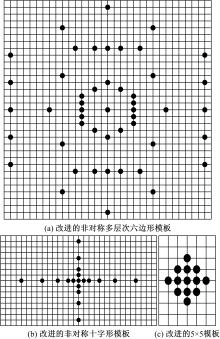
由于运动矢量具有中心偏置的特性, 故可用变增长序列对非对称多层次六边形和非对称十字形模板进行改进。所谓变增长序列是指相邻两数之间间隔按自然数增长的序列^[15], 如1, 2, 4, 7, 11, 16, …或0, 4, 9, 15, 22, …。另外, 原UMHexagonS算法中考虑到自然界中的运动水平方向比垂直方向剧烈, 在搜索时刻意使水平搜索点数多于垂直方向, 从而降低了垂直方向运动剧烈的视频的编码性能, 基于此本文利用多层次旋转六边形进行改进。图3(a)(b)是两者改进后的搜索模板。非对称多层次旋转六边形搜索模板由原来的64个点减少至48个, 非对称十字形搜索模板则由原来的25个点减少到19个, 可见改进之后的模板搜索点数有所减少。对整帧图像来讲, 其减少的搜索点数和降低的编码时间是很可观的, 能在很大程度上提升编码效率。

	Figure Option View Download New Window
	图3 改进的搜索模板Fig.3 Improved search template

2.4.3 自适应搜索方向的引入

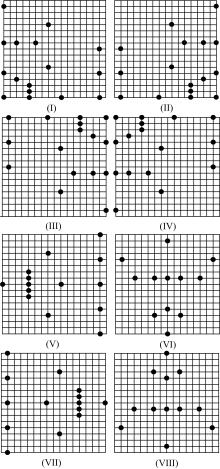
如图3(a)所示的非对称多层次旋转六边形搜索模板中, 共需搜索48个点。为了进一步减少搜索点数, 提高编码效率, 本文根据运动矢量的方向性, 引入了方向自适应搜索技术, 将算法中非对称旋转六边形搜索模板分为如图4所示的8个方向。这样, 可以将搜索点数降低至15(如I, II, III, IV)或13(如V, VII)或11(如VI, VIII)。这样, 对整帧图像和整个视频序列, 其减少的搜索点数目是巨大的, 可提升视频编码效率。方向自适应搜索策略如下:①若当前预测的最优运动矢量PMV在第I象限, 则在第I象限搜索最佳匹配点; 类似地, 在第II, III, IV象限按同样方式搜索; ②若PMV落在坐标轴上, 则根据所在的坐标轴选择相应的方向(V, VI, VII或VIII)进行搜索。

	Figure Option View Download New Window
	图4 自适应搜索方向的划分Fig.4 Partition of adaptive search directon

2.4.4 螺旋5× 5全搜索的改进

根据文献[16]的研究, 最佳点落入以起始搜索点为中心的3× 3矩形范围内的平均比例为98%以上, 与落入5× 5矩形范围内的比例仅差1%左右。可见为了提高1%的精度, 而多搜索16个搜索点是不值得的, 基于此对其进行改进的模板如图3(c)所示。改进后的模板既保证了精度又提升了搜索速度。

2.5 算法描述

MA_DHUS算法流程如图5所示。

	Figure Option View Download New Window
	图5 MA_DHUS算法流程图Fig.5 Flow chart of MA_DHUS algorithm

3 实验结果和性能分析

3.1 测试平台及其配置

首先在VC++6.0平台上将MA_DHUS算法用C语言实现, 并将其集成到H.264标准测试模型JM10.1中。实验所用PC机的硬件配置如下:Intel(R) Core(TM)2 Duo CPU E7400 2.80 GHz, 2.0 G内存。操作系统为WindowsXP 2002+SP2。测试序列集为8个QCIF格式序列, 且均为YUV4∶ 2∶ 0。编码器配置选用JM10.1的基本类(编码配置文件为encoder_baseline.cfg)。实验中主要编码参数为:编码帧数=130, 帧率=30.0, 搜索范围=16, 参考帧数=5, 其他参数为缺省设置, 编码序列格式为IPPP。

3.2 实验结果与分析

3.2.1 改进的六边形算法与原六边形算法性能比较

选取6个测试序列, 分别为silent、foreman、coastguard、city、crew和mobile, 分别采取原六边形算法和改进的六边形算法进行编码, 结果如表1所示。其中HEX、NHEX分别代表原六边形算法和改进的六边形算法。

表1中, 改进的六边形算法与原六边形算法相比, 编码时间平均节省了9.68%, 运动估计时间平均节省了12.12%。码率平均降低1.12%, PSNR值平均提升0.027, 幅度均不大, 所以改进的六边形算法在保证图像质量的前提下, 运动估计时间大幅减少, 提高了编码效率。

表1 改进的六边形算法与原六边形算法性能比较 Table 1 Comparison between HEX and NHEX

3.2.2 MA_DHUS算法与UMHexagonS、FFS和EPZS算法的性能比较

本文算法共包含4个环节, 分别为自适应搜索范围(DSR)、自适应搜索模板(DST)、自适应搜索方向(DSD)和UMHexagonS算法改进。其中自适应搜索方向是在UMHexagonS算法基础上进行优化的, 可以将后两个环节合并为一个环节, 记作DSD_U。为了分析其中每个环节以及本文MA_DHUS算法的效果, 本文对8个序列分别进行了测试, 并与UMHexagonS算法进行对比, 结果如表2所示。表2中↓ 表示PSNR下降, ↑ 表示PSNR提高。

表2 MA_DHUS算法与UMHexagonS算法的性能对比 Table 2 Comparison between MA_DHUS and UMHexagonS

表2中, PSNR最多下降0.04 dB, 最高提升0.09 dB, 表明各个环节和MA_DHUS算法对图像质量的影响不大, 保持了原有图像的质量。经统计发现, 本文算法MA_DHUS比UMHexagonS算法的编码时间平均节省了12.403%, 运动估计时间平均节省了19.124%, 但本文MA_DHUS算法造成了码率的小幅度增加, 但均低于2%, 所以相对于编码时间的减少, 码率的增加量在可以接受的范围内。另外, 对于全局运动视频序列(如mobile)和较剧烈运动视频序列(如crew), 编码速度要明显优于缓慢运动视频序列(如silent)。

MA_DHUS算法与FFS、EPZS算法性能对比如表3所示。由表3可见, 本文算法MA_DHUS针对不同的运动序列均能保持优异的编码性能, 同FS和EPZS算法相比MA_DHUS算法具有以下优点:①视频的重建质量基本保持了原有图像质量:与FS相比, PSNR性能平均提升了0.0112 dB, 最大损失不超过0.02 dB; 与EPZS算法相比, PSNR性能平均提升了0.015 dB, 最大损失不超过0.02 dB; ②编码的压缩效果基本不变:与FS相比, 比特率的增加很少, 平均值为1.316%; 与EPZS相比, 平均值为1.362%; ③编码和运动估计的耗时明显下降:与FS相比, 运动估计速度约为FS的3.459倍; 与EPZS相比, 运动估计时间平均下降了14.113%。MA_DHUS与FS和EPZS相比, 在重建图象质量和码率接近的情况下, 编码效率有了明显的提高。

表3 MA_DHUS算法与FFS、EPZS算法性能对比 Table 3 Comparison among MA_DHUS, FS and EPZS

图6(a)(b)(c)分别是silent序列、mobile序列和harbour序列在FFS、UMHexagonS、EPZS和本文算法MA_DHUS下的R-D性能曲线。可以看出, MA_DHUS算法的R-D性能曲线和FFS、UMHexagonS、EPZS算法的R-D性能曲线非常接近。

	Figure Option View Download New Window
	图6 silent、mobile和harbour序列的R-D性能曲线Fig.6 R-D curves for silent, mobile and harbour

总的来说, 本文算法相对FFS、UMHexagonS和EPZS算法, 明显降低了运动估计开销, 减少了运算量, 而在编码质量方面损失很小, 算法性能比较好。

4 结束语

为了提高编码效率, 本文通过采用搜索范围自适应选取、搜索模板自适应选择、搜索方向自适应决策多重自适应技术以及对UMHexagonS算法中原始混合搜索模板及其搜索策略的改进, 提出了多级自适应快速整像素运动估计算法MA_DHUS。实验结果表明, 该算法适用面广, 针对不同的运动序列均有较好的编码效果。本文算法在保证良好编码性能的前提下, 较FFS、UMHexagonS和EPZS算法分别平均节省了70.290%、19.124%和14.113%的运动估计时间, 有效减少了运动估计的计算量。本文的下一步工作是将该算法移植到DSP系统中, 并针对硬件结构进行代码优化, 进一步提高编码速度。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	张小红, 张东波. H. 264块运动估计自适应快速搜索算法研究[J]. 计算机工程与应用, 2013, 49(6): 183-186. Zhang Xiao-hong, Zhang Dong-bo. Adaptive fast search algorithm for block motion estimation in H. 264[J]. Computer Engineering and Applications, 2013, 49(6): 183-186. [本文引用:1]
[2]	Wu X, Xu W, Zhu N, et al. A fast motion estimation algorithm for H. 264[C]∥IEEE International Conference on Signal Acquisition and Processing, Bangalore, 2010: 112-116. [本文引用:1]
[3]	Cao H, Song G. Improvements of UMHexagonS algorithm for fast motion estimation in H. 264[C]∥Foundations and Practical Applications of Cognitive Systems and Information Processing, Berlin: Springer, 2014: 211-220. [本文引用:1]
[4]	Zhang Z G, Ji C L, Liu Q. A modified motion vector multi-template self-adaptive search algorithm for motion estimation[C]∥IEEE International Conference on Computer Science and Network Technology, Harbin, 2011: 1525-1528. [本文引用:1]
[5]	Zhu C, Lin X, Chau L P. Hexagon-based search pattern for fast block motion estimation[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2002, 12(5): 349-355. [本文引用:1]
[6]	张艳超, 王芳, 赵建, 等. 投影特征峰匹配的快速电子稳像[J]. 光学精密工程, 2015, 23(6): 1768-1773. Zhang Yan-chao, Wang Fang, Zhao Jian, et al. Fast digital image stabilization based on characteristic peak of projection matching[J]. Opt Precision Eng, 2015, 23(6): 1768-1773. [本文引用:1]
[7]	丁鑫, 樊慧津. 基于方向自适应的运动估计混合模板搜索算法[J]. 中国图象图形学报, 2011, 16(1): 14-20. Ding Xin, Fan Hui-jin. A mix-pattern motion estimation search algorithm based on direction adaptation[J]. Journal of Image and Graphics, 2011, 16(1): 14-20. [本文引用:1]
[8]	Tourapis H Y C, Tourapis A M, Topiwala P. Fast motion estimation within the JVT codec[C]∥ICME Meeting, Geneva, Switzerland , 2003. [本文引用:1]
[9]	Chen Z, Zhou P, He Y. Fast integer pel and fractional pel motion estimation for JVT[C]∥The 6th Joint Video Team (JVT) Meeting, Awaji, Japan, 2002: 5-13. [本文引用:1]
[10]	蒋刚毅, 李文锋, 郁梅, 等. H. 264/AVC压缩域鲁棒视频水印[J]. 光学精密工程, 2015, 23(1): 260-270. Jiang Gang-yi, Li Wen-feng, Yu Mei, et al. Robust video watermarking in H. 264/AVC compressed domain[J]. Opt Precision Eng, 2015, 23(1): 260-270. [本文引用:1]
[11]	郭晓珉, 姚睿, 刘智跃, 等. 利用运动强度判据的高效自适应运动估计算法[J]. 中国图象图形学报, 2012, 17(4): 504-511. Guo Xiao-min, Yao Rui, Liu Zhi-yue, et al. Efficient adaptive motion estimation algorithm based on motion intensity[J]. Journal of Image and Graphics, 2012, 17(4): 504-511. [本文引用:2]
[12]	Sun X, Divakaran A, Manjunath B S. A motion activity descriptor and its extraction in compressed domain[C]∥Advances in Multimedia Information Processing-PCM, Berlin: Springer, 2001: 450-457. [本文引用:1]
[13]	吴晓军, 白世军, 卢文涛. 基于H. 264视频编码的运动估计算法优化[J]. 电子学报, 2009, 37(11): 2541-2545. Wu Xiao-jun, Bai Shi-jun, Lu Wen-tao. Optimization on motion estimation algorithm based on H. 264[J]. Acta Electronica Sinica, 2009, 37(11): 2541-2545. [本文引用:1]
[14]	Zhu C, Lin X, Chau L, et al. Enhanced hexagonal search for fast block motion estimation[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2004, 14(10): 1210-1214. [本文引用:1]
[15]	Chen L, Cao J, Tang L, et al. Optimized H. 264 motion estimation algorithm based on UMHexagonS[C]∥The 4th International IEEE Conference on Intelligent Control and Information Processing, Beijing, 2013: 177-181. [本文引用:1]
[16]	吴银花, 金龙旭, 张宁, 等. 针对H. 264改进的快速整像素运动估计算法[J]. 光学精密工程, 2013, 21(4): 1017-1025. Wu Yin-hua, Jin Long-xu, Zhang Ning, et al. Improvement of fast integer pixel motion estimation algorithm for H. 264[J]. Opt Precision Eng, 2013, 21(4): 1017-1025. [本文引用:1]

2013

0.0

. 2013, 49(6):183-186

Adaptive fast search algorithm for block motion estimation in H.264

H.264块运动估计自适应快速搜索算法研究

Zhang Xiao-hong , Zhang Dong-bo.

张小红, 张东波

School of Information Engineering, Jiangxi University of Science and Technology, Ganzhou, Jiangxi 341000, China

Motion estimation is an important issue in H.264 video coding systems because it occupies a large amount of encoding time. So the quality of motion search algorithm affects the entire encoding efficiency directly. A novel search algorithm which utilizes an adaptive hexagon and small diamond search is proposed to enhance search efficiency. The adaptive search pattern is chosen according to the motion strength of the current block. When the block is in active motion, the hexagon search provides an efficient search means; when the block is inactive, the small diamond search is adopted. Simulation results show that this approach can speed up the search process with little effect on distortion performance compared with other adaptive approaches.

H.264视频编解码标准中由于运动搜索部分占整个编码时间的权重很大，所以运动搜索算法的优劣直接影响整个编码的效率。对编码运动估计理论进行了研究，采用六边形和小菱形相结合的方法，提出了一种新的自适应快速搜索算法来改善搜索效率。自适应快速搜索算法模式由当前块运动强度来决定，当当前块处于剧烈运动时，该算法选择六边形图形搜索算法；当当前块处于缓慢运动时，该算法选择小菱形图形搜索算法。实验结果表明该算法相比其他自适应算法以及单纯使用一种搜索图形节约了搜索时间，同时率失真性能影响甚微。

... 264中,运动估计时间占整个编码过程的60%~80%^[1],因此研究快速有效的运动估计算法一直是视频编码领域的热点问题 ...

2010

0.0

... 因此各国学者提出了许多快速算法以减少计算量^[2,3,4],包括三步法(TSS)、新三步法(NTSS)、四步法(FSS)、钻石法(DS)以及基于六边形的搜索法(HEXBS)^[5]等 ...

2014

0.0

2011

0.0

2002

0.0

2015

0.0

... 上述均采用一定的搜索模板,根据运动矢量的中心偏置分布特性^[6],逐步更新下一步搜索方向和模板中心 ...

2011

0.0

. 2011, 16(1):14-20 DOI:10.11834/jig.20110115

A mix-pattern motion estimation search algorithm based on direction adaptation

基于方向自适应的运动估计混合模板搜索算法

Ding Xin , Fan Hui-jin.

丁鑫, 樊慧津

In this paper, a direction-based adaptive mix-pattern motion estimation search algorithm is proposed. The algorithm makes the best of spatial and temporal correlation, which improves the veracity of the search center prediction compared with the algorithms employing spatial correlation only. By employing adaptive threshold technology on static block determination, the disadvantage of const threshold technology on static block determination has been avoided. Moreover, the algorithm chooses the search strategy according to the corresponding motion type, which can balance the video quality and speed simultaneously. Experimental results show that the proposed algorithm can highly reduce the time of motion estimation ensuring the video quality compared with the UMHexagonS algorithm.

提出了一种基于方向自适应的运动估计混合模板搜索算法。该算法利用了运动矢量的时空相关性，对搜索起点进行预测，与仅利用空间相关性预测起点相比，提高了搜索的准确性；然后通过自适应阀值静止块判定技术，对静止块直接中止搜索，解决了常量阀值静止块判定技术仅适应于某种特定序列类型的缺点；最后根据运动类型自适应选择采用小菱形、六边形-小菱形或方向十字-小菱形搜索策略，解决了单一搜索策略模式下，不能兼顾视频压缩图像质量和速度的局限。实验表明，提出算法与H.264标准提供的UMHexagonS算法相比，在保证编码质量的前提下，大大降低了运动估计时间，提高了编码效率。

... 这些算法在很大程度上降低了计算复杂度,但是并没有从全局上考虑运动方向以及运动矢量的相关性^[7],容易陷入局部最优点,导致率失真性能降低,影响运动估计效果 ...

2003

0.0

... 为了提升编码性能,后来提出的EPZS算法^[8]、UMHexagonS算法^[9]等混合了多种技术,如起始搜索点预测、提前终止策略以及混合模板等 ...

2002

0.0

... 为了提升编码性能,后来提出的EPZS算法^[8]、UMHexagonS算法^[9]等混合了多种技术,如起始搜索点预测、提前终止策略以及混合模板等 ...

2015

0.0

... 第三,没有利用运动矢量的方向性^[10],搜索过程中会进行不必要的搜索,影响搜索速度 ...

2012

0.0

. 2012, 17(4):504-511 DOI:10.11834/jig.20120408

Efficient adaptive motion estimation algorithm based on motion intensity

利用运动强度判据的高效自适应运动估计算法

Guo Xiao-min , Yao Rui , Liu Zhi-yue

郭晓珉, 姚睿, 刘智跃

In order to reduce the complexity of motion estimation and improve the efficiency of the video encoder,an adaptive motion estimation search algorithm based on motion intensity is proposed.Motion intensity reflects the intensity of motion between adjacent frames.By defining the concept of motion intensity,the movement of the next frame is predicted based on the measured intensity information of the current frame,and a different motion search algorithm is selected adaptively.If the motion intensity of the current frame is greater than the threshold,the UMHexagonS search algorithm is chosen,otherwise the improved hexagon search algorithm is chosen.Simulation results show that the coding efficiency is improved significantly,while the image quality and compression performance change little.In addition,the threshold of motion intensity in the algorithm is adjustable,thus the demands of different encoding can be met by changing the threshold.

为减少运动估计计算量,提高视频编码效率,提出了基于运动强度的自适应运动估计搜索算法。该算法通过定义运动强度概念来反映帧间图像运动的剧烈程度,依据当前帧的运动强度信息预测下一帧运动情况,并自适应选择算法进行运动搜索:当运动强度高于设定阈值时选用UMHexagonS算法,低于该阈值时选用改进的六边形算法。实验仿真结果表明,该算法能在保证图像质量和压缩效果的基础上,大幅提高编码效率,并可通过调节阈值大小满足不同编码要求。

... 然而,其运动活性是按镜头提取的,由于实际视频中视频镜头非常短,故运动活力无法很好地描述视频中每帧图像运动的剧烈程度^[11] ...

... 为此,本文定义帧级运动强度(Frame motion intensity)的概念,描述每帧图像的运动程度,并借鉴运动活性^[11,12]的计算方法进行分析 ...

2001

0.0

... 为此,本文定义帧级运动强度(Frame motion intensity)的概念,描述每帧图像的运动程度,并借鉴运动活性^[11,12]的计算方法进行分析 ...

2009

0.0

. 2009, 37(11):2541-2545

Optimization on motion estimation algorithm based on H.264

基于H.264视频编码的运动估计算法优化

Wu Xiao-jun , Bai Shi-jun , Lu Wen-tao.

吴晓军, 白世军, 卢文涛

Harbin Institute of Technology Shenzhen Graduate School,Shenzhen,Guangdong 518055,China

Motion estimation (ME) is vital to video compression.Due to the adoption of the high precision of motion vector (MV) in H.264 encoder,the computational cost increases rapidly,and ME takes almost 80% encoding time.In this paper,based on the UMHexagonS algorithm,an optimized algorithm is proposed based on the dynamic search range selection,big hexagon and small hexagon search mode respectively,which saves ME time effectively without quality loss.Experimenting with some typical video sequences proves that,compared to UMHexagonS algorithm,our optimized algorithm can save about 18.292% ME time and reduce the complexity of original scheme as well as enhance the real-time performance of the encoder but almost has no change in the reconstructed picture quality and bitrate.

运动估计是视频压缩中最重要的环节.H.264编码器由于采用了高精度运动矢量,计算量迅速增长,运动估计消耗整个编码时间80％左右.本文在分析UMHexagonS算法的基础上,分别对UMHexagonS算法中搜索窗口大小的选择、大六边形搜索和小六边形(小钻石)搜索模式三方面做了优化,在保持了原有图象质量的情况下有效的节省了运动估计时间.通过对各种测试序列的实验证明,优化后的算法与UMHexagonS算法相比,在重建图象质量和码率接近的情况下,运动估计时间平均节省了18.292%,降低了算法的复杂度,提高了编码器的实时性.

2004

0.0

2013

0.0

... 所谓变增长序列是指相邻两数之间间隔按自然数增长的序列^[15],如1,2,4,7,11,16,…或0,4,9,15,22,… ...

2013

0.0

. 2013, 21(4):1017-1025 DOI:10.3788/OPE.20132104.1017

Improvement of fast integer pixel motion estimation algorithm for H.264

针对H.264改进的快速整像素运动估计算法

Wu Yin-hua , Jin Long-xu , Zhang Ning

吴银花, 金龙旭, 张宁

Changchun Institute of Optics, Fine Mechanics and Physics,Chinese Academy of Sciences

On the basis of the UMHexagonS algorithm used in the Joint Model(JM) for H.264, a new fast algorithm on integer pixel motion estimation was proposed to improve the video encoding characteristics. A new order of checking predicted Motion Vector(MV) was proposed in the predicting starting search point to promote the accuracy of starting search point. Then, a self-adaptive global search method was proposed for the global search, by which the unsymmetrical-cross search and uneven multi-hexagon-grid search could be skipped based on the relationship between two predicted MVs with highest accuracy, and the feasibility and accuracy of this judging method was verified through tests on a number of different sequences. Meanwhile, an improved 5×5 search method was presented according to the distribution of best MV relative to the starting search point and a new early termination technique for sub-macroblock was added to further reduce the cost of motion estimation without additional computation. According to the experiment results, the proposed algorithm reduces the total number of search points by 83.80% and the Peak Signal to Noise Ratio(PSNR) about 0.021 dB on average and increases an average increment of 0.46% on equivalent bitrates as compared with that of original UMHexagonS algorithm. With a negligible performance degradation, the proposed algorithm reduces the computation of motion estimation effectively and offers a well-distributed effect on sequences with different motion intensities.

以视频压缩标准H.264联合开发模型（JM）中的运动估计算法UMHexagonS为基础，提出了一个新的快速整像素运动估计算法来改进压缩编码性能。在起始搜索点预测部分，提出了新的预测运动矢量（MV）检测顺序，以提高起始搜索点的准确度；在全局搜索部分提出了自适应全局搜索方法，根据准确度最高的两个预测MV之间的关系，适当跳过非对称十字型模板搜索和非均匀多重六边形模板搜索，并通过对不同序列的测试，验证了判断准则的可行性与准确性。根据实际序列中最佳MV相对起始点的分布，提出了改进5×5搜索。另外，增加了针对子宏块的提前终止策略，在不增加额外运算量的前提下，进一步减少了运动估计开销。实验结果表明，相对UMHexagonS算法，提出的改进算法使搜索点总数平均减小了83.80%，信噪比平均下降了0.021 dB，或输出码率等效增加了0.46%。该算法有效降低了运动估计的运算量，而只带来了很小的编码性能下降，且对不同运动强度的视频序列具有均匀的算法效果。