进行后悬架扭转梁总成有限元建模时, 先将其三维模型导入有限元前处理软件中, 然后选用壳单元进行网格划分, 共离散为25 913个单元和26 380个节点, 得到该扭转梁有限元模型如图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 后悬架扭转梁总成有限元模型Fig.1 Finite element model of twist beam

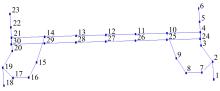
采用Lanczos法对建立的扭转梁总成有限元模型在无约束自由状态下进行模态分析, 提取其前6阶固有频率和模态振型, 并与自由模态试验结果进行对比。基于试验模态分析理论, 采用单输入/多输出识别法对扭转梁总成进行试验模态分析, 试验过程中通过橡皮软绳将扭转梁总成悬吊起来, 使其处于如图2所示的自由状态, 采用力锤施加脉冲激振力, 利用三向振动加速度传感器拾取扭转梁总成各测点的振动加速度信号, 扭转梁总成上各测点布置如图3所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 扭转梁总成模态试验现场Fig.2 Modal test of twist beam

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 测点布置示意图Fig.3 Nodes layout diagram

将扭转梁总成前6阶非刚体自由模态频率和振型的仿真分析与试验结果进行对比, 如表1所示。

表1

Table 1

表1(Table 1)

表1 扭转梁总成仿真分析与模态试验结果对比 Table 1 Comparison between simulation and testing mode 模态阶次 固有频率/Hz 相对误差/% 模态振型 仿真值 试验值 1 36.84 38.01 -3.18 一阶扭转 2 67.17 68.49 -1.97 一阶弯曲 3 103.54 99.86 3.55 局部扭转 4 109.05 106.07 2.73 局部弯曲 5 137.39 138.78 -1.01 二阶弯曲 6 177.63 173.79 2.16 二阶扭转

表1 扭转梁总成仿真分析与模态试验结果对比 Table 1 Comparison between simulation and testing mode

从表1中可见, 扭转梁总成前6阶模态振型一致, 固有频率的仿真分析与试验结果比较接近, 最大相对误差小于4%, 说明该扭转梁总成有限元模型是准确合理的。

由于有限元模型自由度数目庞大, 在建立柔性体模型时, 采用模态综合法对有限元模型进行超单元分析, 并定义超单元与其他部件连接的外部节点, 通过主模态和约束模态组成的超单元假设模态代替原完备模态, 生成可用于多体动力学仿真分析的柔性体模型^[7]。选取后悬架扭转梁总成的前20阶非刚体模态, 定义扭转梁总成与悬架、车身和车轮等部件连接的外部节点共8个, 建立扭转梁总成柔性体模型如图4所示。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 后悬架扭转梁总成柔性体模型Fig.4 Flexible model of twist beam

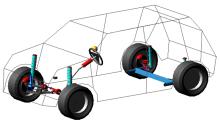
利用Adams软件建立整车刚柔耦合模型时, 将扭转梁总成柔性体模型导入到后悬架子系统中, 通过外部节点完成与其他部件的约束连接。按照各子系统间的拓扑关系, 将车身、前悬架、后悬架、转向系、制动系和轮胎等子系统模型通过通讯器完成相互之间的装配连接, 最后得到轿车整车刚柔耦合虚拟样机模型如图5所示。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 整车刚柔耦合模型Fig.5 Rigid-flexible coupling vehicle model

使整车刚柔耦合模型在满载状态下分别以20、40、60、80、100、120 km/h的车速在构建的B级路面上匀速行驶, 进行整车行驶平顺性仿真分析, 提取驾驶员座椅处车身地板的振动加速度响应, 并与实车试验结果进行对比验证。

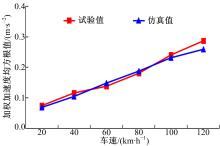
按照国家标准GB/T4970-2009《汽车平顺性试验方法》中规定的加权加速度均方根值计算方法, 计算出驾驶员座椅处地板振动的总加权加速度均方根值随车速变化的仿真和试验结果, 如图6所示。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 总加权加速度均方根值随车速变化曲线Fig.6 Overall weighted acceleration RMS vs vehicle speed

从图6可以看出, 随着车速的增加驾驶员座椅地板处总加权加速度均方根值的仿真和试验结果均呈逐渐增大的趋势; 两者的变化趋势基本一致, 数值上略有差别, 最大相对误差小于9.7%, 从而验证了所建整车刚柔耦合虚拟样机模型的正确性, 能够用于后悬架扭转梁疲劳寿命研究。

在整车刚柔耦合模型中, 扭转梁总成柔性体模型的弹性位移可通过模态矢量和模态坐标的线性组合来表示^[8], 其任一点的广义坐标可定义为:

q=x, y, z, ϕ, θ, φ, ξiT=R, Ψ, ΦT1

式中:(x, y, z)为局部坐标系在总体坐标系中的位置; (ϕ , θ , φ )为局部坐标系在总体坐标系中的欧拉角; ξ _i为柔性体的第i阶模态位移; (R, Ψ )为坐标的矢量表达; Φ 为ξ _i的矢量表达, 即模态位移矢量。

模型的拉格朗日动力学方程为:

Mq··+M·q·-12∂M∂qq·Tq·+Kq+G+Cq·+∂Ω∂qTλ=Q2

式中:M、K、C分别为扭转梁总成柔性体的质量矩阵、刚度矩阵和阻尼矩阵; G为重力; λ 为约束方程的拉格朗日乘子; Q为广义力矩阵。

求解式(2)可得q, 进而得到模态位移矢量Φ 及其各阶模态位移ξ _i。结合模态分析得到的第i阶固有频率ω _i和模态振型矢量ϕ _i, 基于模态应力恢复算法可求得有限元模型上节点的模态应力σ 和反作用力F分别为:

σ=ΦEσF=KU-ω2MU3

式中:E_σ 为模态应力矩阵, 由材料的弹性模量和泊松比决定; ω 为模态圆频率, 是ω _i的矢量表达; U为节点位移, 通过模态振型矢量ϕ _i和模态位移矢量Φ 进行定义。

通过式(3)求解得到柔性体节点应力σ 和反作用力F的时间历程, 可作为结构疲劳寿命分析的载荷谱。

汽车试验场的耐久性试验道路包括比利时路、鹅卵石路、扭曲路、搓板路等典型路面, 可进行汽车的疲劳强化试验, 大幅缩短汽车耐久性试验周期^[9]。其中, 比利时路是随机输入型道路, 与实际道路统计特性比较接近, 是耐久性试验中最普遍采用的道路之一。此外, 鹅卵石路可提供较大的纵向和横向冲击激励, 搓板路属于周期性的简谐振动路面, 可用来考查汽车强迫振动下的疲劳强度^{[10, 11]}。因此, 选择这3种典型耐久性路面构建虚拟试验场耐久性强化组合路面模型, 可较全面的反映真实路面激励特征, 给汽车输入足够的激振载荷。参考安徽定远汽车试验场相应的耐久性试验规范, 构建鹅卵石路、搓板路和比利时路虚拟路面模型, 并根据各路面所占行驶里程, 生成长度为160 m的耐久性强化试验组合路面模型, 如图7所示。其中鹅卵石路长度为40 m, 搓板路长度为40 m, 比利时路长度为80 m, 所占比例分别为25%、25%和50%。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 汽车耐久性强化试验组合路面Fig.7 Durability enhancement road

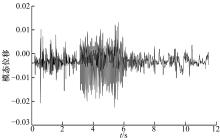
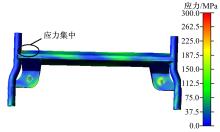
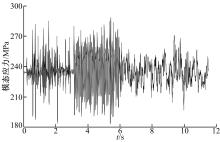
使整车刚柔耦合虚拟样机模型在满载工况下以50 km/h的车速在耐久性强化试验路面上行驶, 进行整车耐久性仿真分析, 计算时间为11.5 s, 对应的行驶里程约为160 m。提取扭转梁总成柔性体模型各阶模态位移的时间历程, 并采用模态应力恢复方法得到扭转梁总成模型各节点的应力时间历程。图8给出了扭转梁总成柔性体模型的第2阶模态位移时间历程, 图9为某时刻扭转梁总成应力分布图, 图10是应力集中处某节点的应力时间历程。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 第二阶模态位移时间历程Fig.8 Modal displacement time history of mode 2

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 后悬架扭转梁总成应力云图Fig.9 Stress contour of twist beam

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 节点应力时间历程Fig.10 Node stress time history

由图10可见, 仿真过程中该节点的最大应力值为281.06 MPa, 出现在时间历程的1.56 s处(鹅卵石路面), 仿真得到的后悬架扭转梁应力时间历程可用于疲劳寿命预测。

汽车后悬架扭转梁结构的疲劳失效通常为低载高周疲劳破坏, 一般采用名义应力法(S-N法)进行疲劳寿命计算, 该方法通过S-N曲线将疲劳寿命与应力之间的关系描述为^[12]:

σa=σ'f2Nf)b4

式中:σ _a为应力幅; σ '_f为疲劳强度系数; b为疲劳强度指数; N_f为载荷循环次数。

S-N曲线一般通过零均值载荷下的疲劳试验测取, 而汽车扭转梁总成结构所受载荷历程通常为非零均值随机载荷, 可采用Goodman法对非等幅应力进行修正, 即:

σe=σa1-(σm/σu)5

式中:σ _e为等效零均值应力幅; σ _m为应力均值; σ _u为极限拉伸强度。

基于Palmgren-Miner线性疲劳损伤累计理论, 变幅载荷下零部件的疲劳损伤和疲劳寿命分别定义为:

D=∑i=1kniNfi≤1, N=1D6

式中:k为变幅载荷的应力水平级数; n_i是第i级载荷的循环次数; N_fi为第i级载荷下的疲劳寿命; D为总疲劳损伤; N为疲劳寿命。

基于上述理论方法, 在MSC.Fatigue软件中创建后悬架扭转梁材料的S-N曲线, 设置存活率为95%, 将整车动力学仿真获得的扭转梁应力时间历程导入, 采用名义应力法计算后悬架扭转梁疲劳寿命, 并选择Goodman法修正平均应力对疲劳寿命的影响, 得到扭转梁疲劳寿命云图如图11所示。

图11

Fig.11

	Figure Option ViewDownloadNew Window
	图11 后悬架扭转梁总成疲劳寿命云图Fig.11 Fatigue life contour of twist beam

由图11可看出, 扭转梁最小疲劳寿命出现在横梁与纵臂连接处, 即图中位置P处, 最小循环寿命值为1.24× 10⁵个载荷循环, 根据强化路面的长度换算成耐久性强化路面疲劳寿命里程数为1.24× 10⁵× 0.16=19 840 km。

汽车在用户路面行驶时, 扭转梁的疲劳寿命里程可通过强化路面的强化系数计算得到, 强化系数定义为^[11]:

K=L0/Lp7

式中:K为强化系数; L₀为用户路面失效里程; L_p为强化路面失效里程。

组合强化路面的综合强化系数可定义为:

KΣ=∑i=13wiKi8

式中:K_Σ 为组合强化路面的综合强化系数; w_i为第i段强化路面所占比例; K_i为第i段强化路面的强化系数。

本文所建立的强化组合路面模型包括3种强化路面, 根据文献[11]可知鹅卵石路、搓板路和比利时路的强化系数分别为5.8、4.9和12.6, 根据式(8)和各强化路面所占比例, 可得组合强化路面的强化系数为5.8× 0.25+4.9× 0.25+12.6× 0.5=9.0。因此扭转梁最小疲劳寿命为19 840× 9=178 560 km, 满足耐久性道路试验中汽车零部件疲劳寿命大于100 000 km的要求^[13], 且扭转梁总成的疲劳寿命有一定余量, 存在进一步轻量化的空间。

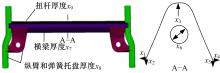
基于网格变形技术, 采用商业软件DEP Meshworks/Morpher建立后悬架扭转梁总成参数化模型, 定义6个形状变量和3个厚度变量(记为x₁, x₂, …, x₉)如图12所示, 由于扭转梁横梁截面为对称结构, 则有x₂=x₅, x₁=-x₄。表2给出了各设计变量的取值范围。

图12

Fig.12

	Figure Option ViewDownloadNew Window
	图12 参数化模型及设计变量Fig.12 Parametric model and design variables

表2

Table 2

表2(Table 2)

表2 设计变量取值范围 Table 2 Value range of design variables 设计变量 变量描述 初始值 下限 上限 x1/mm 横梁左侧底部水平移动 0 -10 10 x2/mm 横梁左侧底部垂直移动 0 -10 10 x3 横梁圆弧缩放系数 1.0 0.8 1.2 x4/mm 横梁右侧底部水平移动 0 -10 10 x5/mm 横梁右侧底部垂直移动 0 -10 10 x6 扭杆半径缩放系数 1.0 0.8 1.2 x7/mm 横梁厚度 4.4 3.4 5.4 x8/mm 纵臂和弹簧托盘厚度 4.0 3.0 5.0 x9/mm 扭杆厚度 2.8 1.8 3.8

表2 设计变量取值范围 Table 2 Value range of design variables

为提高优化效率, 采用Kriging近似模型代替仿真模型来表达各设计变量和响应之间的关系, 根据最优拉丁方试验设计方法在每个设计变量取值范围内均匀随机采样, 参考各设计变量取值范围和拟合精度要求选取81个样本点拟合各响应的Kriging近似模型。可通过决定系数R²检验各近似模型的精度, 其表达式为:

R2=∑i=1ny^i-y-2∑i=1nyi-y-29

式中:n为用于检验模型精度的数据点数量; y^i为第i个响应的近似模型预测值; y_i为第i个响应的仿真值; y-为平均值。

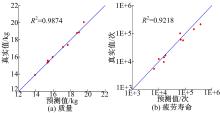
决定系数R²的取值范围是[0, 1], 其值越接近于1, 说明近似模型可信度越高。额外随机选取10个样本点对近似模型精度进行检验, 得到后悬架扭转梁质量、疲劳寿命、一阶扭转模态频率和扭转刚度近似模型的决定系数分别为0.9874、0.9218、0.9702、0.9738, 其中质量和疲劳寿命近似模型的检验结果如图13所示, 可见各近似模型均满足精度要求。

图13

Fig.13

	Figure Option ViewDownloadNew Window
	图13 Kriging模型精度检验Fig.13 Precision validation of Kriging model

综合考虑质量、疲劳寿命、刚度和模态等性能指标, 对后悬架扭转梁总成进行轻量化多目标优化设计, 优化的数学模型可描述为:

min(m(x), -N(x))s.t.kt(x)-kt0≤0.1kt0ft(x)-ft0≤0.1ft0x∈xL, xU10

式中:m(x)为后悬架扭转梁总成质量; N(x)为扭转梁总成的最小疲劳寿命; k_t(x)、k_t0分别为扭转梁总成的扭转刚度值及其初始值, k_t0=38.28 N· m/(° ); f_t(x)、f_t0分别为一阶扭转模态频率及其初始值, f_t0=36.84 Hz; x为设计变量, x_L和x_U分别为各设计变量取值的下限和上限。

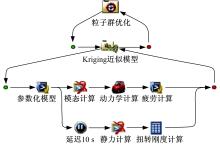
将各性能指标计算组件集成到多学科优化分析平台Isight软件中, 选择粒子群多目标优化算法, 建立基于Kriging近似模型的后悬架扭转梁总成轻量化多目标优化分析模型, 如图14所示。

图14

Fig.14

	Figure Option ViewDownloadNew Window
	图14 多目标优化分析模型Fig.14 Multi-objective optimization model

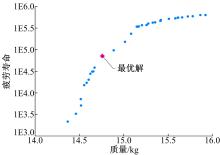
定义粒子群算法的粒子群规模为80, 迭代的代数为120, 优化得到Pareto前沿如图15所示。

图15

Fig.15

	Figure Option ViewDownloadNew Window
	图15 Pareto前沿Fig.15 Pareto frontier

由图15可知, 后悬架扭转梁总成的质量和疲劳寿命两个目标函数之间是相互矛盾的, 其中一个目标函数达到最优要以牺牲另外一个目标函数为代价。由于是针对扭转梁总成的轻量化研究, 在保证扭转梁疲劳寿命满足设计要求的同时, 尽量使扭转梁总成质量最小, 因此选择Pareto前沿中满足扭转梁总成疲劳寿命要求且使其质量相对较小的解作为最优解, 根据工程实际对设计变量优化结果进行修正, 得到优化前后设计变量具体数值如表3所示。

表3

Table 3

表3(Table 3)

表3 优化前后的设计变量 Table 3 Design variables before and after optimization 设计变量 初始值 优化值 修正值 x1/mm 0 -2.5561 -2.56 x2/mm 0 -4.1699 -4.17 x3 1.0 0.8681 0.88 x4/mm 0 2.5561 2.56 x5/mm 0 -4.1699 -4.17 x6 1.0 1.0286 1.03 x7/mm 4.4 2.6596 2.7 x8/mm 4.0 3.2825 3.3 x9/mm 2.8 2.3942 2.4

表3 优化前后的设计变量 Table 3 Design variables before and after optimization

为验证后悬架扭转梁轻量化效果, 将设计变量修正值赋予仿真模型, 计算扭转梁各项性能指标, 并与优化前的性能指标进行对比, 如表4所示。图16给出了扭转梁总成轻量化设计后疲劳寿命云图。

表4

Table 4

表4(Table 4)

表4 优化设计结果 Table 4 Optimization results 性能指标 初始值 优化设计 变化量/% 质量/kg 18.53 14.76 -20.35 疲劳寿命/km 178 560 118 368 -33.71 一阶扭转模态频率/Hz 36.84 34.28 -6.94 扭转刚度/[N· m/(° )-1] 38.28 35.15 -8.18

表4 优化设计结果 Table 4 Optimization results

图16

Fig.16

	Figure Option ViewDownloadNew Window
	图16 优化后扭转梁总成疲劳寿命云图Fig.16 Fatigue life contour of optimized twist beam

由表4和图16可知, 通过多目标粒子群优化算法对Kriging近似模型进行迭代寻优, 使得后悬架扭转梁总成质量降低了3.77 kg, 比初始设计减少质量20.35%, 轻量化效果比较明显。同时, 扭转梁一阶扭转模态频率和扭转刚度变化不大, 最小疲劳寿命为8.22× 10⁴, 换算成里程数约为118368 km, 满足设计要求。