公交拥挤可视为一种非市场商品(Non-market goods), 并不能直接量化其相关成本。通常情况下, RP(Revealed preference)和SP(Stated preference)调查法是确定拥挤程度对出行者出行行为影响的两种基本方法, 其中:SP调查是为获取“ 假定条件下受访者对多个方案所表现出来的主观偏好” 而进行的意愿调查, 而RP调查是针对某些已经实施的政策、措施或已经存在的交通设施而对被调查者实际出行行为进行的调查^[5]。

条件价值法(Contingent valuation method, CVM)最初是由Cifiacy-wantrup^[11]提出, 目前被广泛应用于成本效益分析以及环境影响评价等非市场价值评估方面。其核心思想是利用效用最大化原理, 以得到商品或服务的价值为目的, 借助问卷调查直接询问被调查者对某个商品或某项服务在发生数量或质量变化时的支付意愿(Willingness to payment, WTP), 以此揭示被调查者对商品和服务的偏好^[12]。条件价值法的一个核心内容是用于确定受访者对商品或服务最大支付意愿的引导技术(问卷格式), 目前常用的引导技术包括投标博弈、支付卡格式、开放式问卷和二分选择方法等。二分选择法只需被调查者针对特定场景中给定的最大支付意愿回答“ 是” 或“ 否” , 比直接回答最大支付意愿更能反映模拟市场的定价行为^[13], 在CVM研究中被广泛应用。

对于公交拥挤的成本量化而言, 根据条件价值法的基本思想, 首先以效用最大化为目的, 建立公交乘客j在拥挤水平i时的效用函数U_{i, j}。本文主要考虑出行费用p_j与车内行程时间t_j, 并加入出行者的个人属性项X_j(如年龄、收入等), 如式(1)所示, 其中考虑到拥挤状况下的单位时间令人更加难捱, 将拥挤作为出行时间价值的影响因素, 故系数μ _{2, i}的取值与拥挤水平有关。假设拥挤水平i=0为不拥挤情况, 则当票价与乘车时间均相等时, 拥挤水平i=0的效用值肯定要大于拥挤水平i(i≠ 0)的效用值, 即U_{0, j}> U_{i, j}。

Ui, j=μ0+μ1pj+∑iDiμ2, itj+θXj+εi, j1

式中:μ ₀为常数项; μ ₁为费用的系数; μ _{2, i}为车内行程时间的系数; θ 为出行者个人属性对应的系数; D_i为不同拥挤水平下的哑变量, 若为当前拥挤水平i则D_i=1, 否则为0; ε _{i, j}为随机项。

其次通过问卷调查得到乘客对公交拥挤的偏好或是支付意愿, 进而评价公交拥挤水平发生变化时的个人支付意愿。其基本思想是当拥挤水平发生变化时, 用额外时间来表征支付意愿(WTP), 使得两种拥挤水平下的效用值相同(U_{i, j}=U_{0, j}), 如式(2)所示。将支付意愿转化为货币形式即可得到拥挤成本。

μ0+μ1pj+μ2, 0tj+WTP+θXj+ε0, j=μ0+μ1pj+μ2, itj+θXj+εi, j2WTP=μ2, iμ2, 0-1tj-εjμ2, 03

式中:ε _j≡ ε _{i, j}-ε _{0, j}。

不同拥挤水平i下的时间价值P_{v, i}是效用函数中时间与费用的边际替代率, 如式(4)所示。把式(4)代入式(3)中, 则WTP转化为时间价值的函数。而时间价值与车内拥挤程度存在正相关关系, 故进一步建立以拥挤度为自变量的拥挤时间价值模型, 以便测算任何拥挤程度下的拥挤成本。

Pv, i=∂Ui, j/∂tj∂Ui, j/∂pj=μ2, iμ14WTP=Pv, iPv, 0-1tj-εjμ2, 05

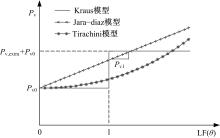
关于时间价值与车内拥挤程度的研究, Kraus^[8]首先提出了将车内时间价值分为两类, 一类是有座情况下的车内时间价值P_v=P_v0, P_v0为不拥挤情况下的时间价值; 另一类是拥挤情况下的车内时间价值P_v=P_v0+P_{v, extra}, P_{v, extra}是站立乘客额外感知时间价值, 其表达式如式(6)所示。

Pv, i=Pv0, 有座情况下Pv0+pv, extra, 无座情况下6

针对无座情况, 车内时间价值仍与乘载率LF相关, Jara-dí az和Gschwender^[9]在Kraus常数分段函数的基础上对车内时间价值函数进行改进, 认为P_{v, extra}为非常数, 而是随着乘载率LF线性增加, 如式(7)所示:

Pv=Pv0+Pv1×LF7

式中:P_v1为拥挤的边际价值; LF为乘客数与公交车座位数的比值, 能同时反映拥挤与不拥挤的状态, 故文中亦采用LF作为车内拥挤程度的表征指标。

虽然线性模型应用广泛, 但是与实际调查数据出入较大。Douglas和Karpouzis^[4]在研究澳大利亚轨道交通拥挤成本时发现, 车内时间价值P_v与乘载率LF呈现非线性关系。因此, Tirachini等^[10]将时间价值函数P_v进一步改进为一元二次函数, 文中用占有率θ (实际乘客数与满载乘客数的比值)替代LF表征拥挤水平, 如式(8)所示:

Pv=Pv01-0.2381θ+1.1905θ28

图1为上述3种模型的图形描述。虽然基于拥挤的车内时间价值模型得到进一步的改进, 但是仍然存在以下问题:①Kraus模型中以LF=1为分界, 当LF< 1时认为没有拥挤影响, 然而在公交拥挤初步调查中发现:当只有少量座位时, 乘客间的个人空间较小, 存在压迫感, 部分乘客更倾向于选择站立, 因此将LF=1作为有无拥挤影响的分界点是不适当的, 文中采用美国公交通行能力与服务质量手册^[14](Transit capacity and quality service manual, TCQSM)对公交拥挤的服务质量(Quality of service, QOS)的分级, 选取QOS B作为有无拥挤影响的分界点, 即LF=0.8; ②当LF≤ 0.8时, 乘客对拥挤的感知并不明显, 此时可以认为时间价值是相等的, 等于P_v0, 而Jara-dí az以及Tirachini提出的模型都认为时间价值是随着LF单调递增的, 与实际不相符; ③当LF> 0.8时, 乘客需要站立, 随着LF的增加乘客对拥挤的感知越来越明显, Kraus提出的常数模型不符合实际情况; ④需要考虑乘载率LF的取值差异, Tirachini在标定模型时LF的最大值为1.75, 而鉴于国内高峰期间公交车内满载的常态化, 在标定模型参数时需要考虑满载情况。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 考虑拥挤的时间价值示例Fig.1 Crowding VOT of above three models

结合上述3个模型以及存在的问题, 建立拥挤时间价值的非线性分段函数:当LF≤ 0.8时拥挤时间价值为0; 当LF> 0.8时为非线性递增函数, 在线性模型的基础上加入指数项; 其表达式如式(9)所示。需要说明的是, 当超过公交车的满载乘客数以后时, 拥挤时间价值仍是非线性增加。但当达到公交车再也无法多容纳一名乘客时, 乘客则需要改乘下一趟公交车或选择其他出行方式。其中将非线性函数中P_v0的系数项记为拥挤动态影响系数c(LF), 用以表征不同拥挤程度对时间价值的影响。

Pv, cr=0, 0≤LF≤0.8αLF-0.8e-βLF-0.82Pv0, LF> 0.89cLF=αLF-0.8e-βLF-0.8210

式中:α 、β 为相关系数。

不同拥挤水平的乘客车内时间价值为不拥挤的时间价值与拥挤时间价值之和, 如式(11)所示。

Pv=Pv0+Pv, cr11

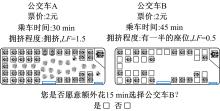
本文采用CVM广泛应用的引导技术— — 二分选择法调查乘客对公交车内拥挤的支付意愿。问卷调查表格主要包括两个部分:一部分是个人属性调查, 主要包括性别、年龄、职业、收入、出行方式; 另一部分为情景调查, 在特定的拥挤水平下询问被调查者是否愿意额外支出预设的时间改乘相对不拥挤的公交车辆。针对拥挤水平分级, TCQSM将公交拥挤的服务质量分为A~F共6级, 如表1所示。而国内对公交拥挤水平进行分级的相关研究较少, 《客车装载质量计算方法》(GB/T 12428-2005)规定每0.125 m²核定站立乘客1人。以常规公交车为例, 座位数在40个左右, 有效站立面积为8 m², 则满载乘客数在100人左右, 因而得到满载时的LF值为2.5, 故0≤ LF≤ 2.5。结合TCQSM的研究结论, 在问卷调查中将LF分为0.5、0.8、1.0、1.25、1.5、2.0、2.5这7个级别, 分别对应i=0~6。通过初步调查公交满载与有半数空座两种拥挤情况时乘客的最大时间支付意愿, 确定将额外时间分为5、10、15、20 min。将拥挤水平i与额外时间随机组合, 形成多组情景, 图2为其情景之一。课题组于2014年3~4月, 在杭州市开展了公交车内拥挤成本问卷调查。

表1

Table 1

表1(Table 1)

表1 拥挤服务质量分类[14] Table 1 Fixed-route passenger load QOS QOS 乘载率LF 乘客角度描述 A 0~0.5 乘客间可随意选择座位 B 0.5~0.8 乘客可适当选择座位 C 0.8~1.0 所有乘客都有座位, 选择性小 D 1.0~1.25 20%的乘客需站立, 但仍有个人空间 E 1.25~1.5 1/3的乘客需站着, 部分身体接触, 有压迫感 F > 1.5 拥挤, 乘客间有明显身体接触, 压迫感强烈

表1 拥挤服务质量分类[14] Table 1 Fixed-route passenger load QOS

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 SP调查问卷示例Fig.2 Example of SP questionnaire

对于问卷调查中公交车A与公交车B, 如果乘客j选择增加额外的乘车时间Δ t保障乘车舒适性, 那么该乘客认为公交车B的效用值 UBi, j大于公交车A的效用值 UAi, j, 即 UBi, j> Ui, jA。故乘客j选择增加时间而保障乘车舒适性的概率为:

Pr(yesj)=Pr(UBi, j> UAi, j)=Pr(μ0+μ1pj+μB2, i(tj+Δt)+θXj+εBi, j> μ0+μ1pj+μA2, itj+θXj+εAi, j)=Prεj< μBB2, itj+Δt-μA2, itj12

为了便于计算, 令θ =ε /σ , 将ε _j~N(0, σ ²)转化成标准正态分布N(0, 1), 从而得到Probit模型, 如式(13)所示。并根据调查问卷数据, 运用最大似然估计思想通过统计分析软件EVIEWS标定相关系数。

Pr(yesj)=ΦμB2, iσ(tj+Δt)-μA2, iσtj13

Probit模型估计结果如表2所示, 可以看出, |Z|> Z_0.05=1.96, 说明模型估计的系数在统计上是显著的, 从而表明车内拥挤对时间价值有显著影响, 并且μ _{2, i}随着拥挤程度的增加而增加。

表2

Table 2

表2(Table 2)

表2 Probit模型估计结果 Table 2 Estimation result of Probit model 乘载率LF μ 2, i Z统计值 0.5 -0.117 325 -8.090 231 0.8 -0.120 256 -7.773 971 1.0 -0.133 135 -7.596 299 1.25 -0.141 685 -7.234 568 1.5 -0.161 106 -7.567 904 2.0 -0.189 269 -7.810 124 2.5 -0.205 398 -8.036 483

表2 Probit模型估计结果 Table 2 Estimation result of Probit model

以LF=0.5时的时间价值作为不拥挤的时间价值, 即P_v0=P_{v, 0}=μ _{2, 0}/μ ₁。结合式(4)和式(11)计算拥挤动态影响系数, 简化得到表达式(14):

cLFi=μ2, iμ2, 0-1, i=1, 2, …, 6(14)

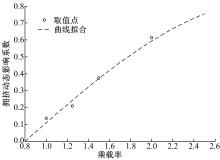
其计算结果如表3所示。

表3

Table 3

表3(Table 3)

表3 不同拥挤水平下的c(LF)值 Table 3 c(LF)under different load factors 乘载率LF c(LF) 乘载率LF c(LF) 0.5 0.000 1.5 0.373 0.8 0.025 2.0 0.613 1.0 0.135 2.5 0.751 1.25 0.208

表3 不同拥挤水平下的c(LF)值 Table 3 c(LF)under different load factors

根据表3的数据, 采用最小二乘法对c(LF)进行曲线拟合(见图3), 标定各个参数, 结果如式(15)所示:

c(LF)=0.55(LF-0.8)e-0.074(LF-0.8)2LF> 0.8 (R2=0.9945)(15)

式中:R²=0.9945, 说明拟合结果好。如果仅考虑LF≤ 2.0的值, 线性拟合效果也较好, 此时R²=0.9928, 故在国外公交车内拥挤研究中线性模型应用广泛。而国内高峰期间公交乘载率普遍大于2.0, 同时在调查问卷中发现当LF> 2.0时乘客对于拥挤程度感知变缓, 认为都很拥挤, 即时间价值增加趋势变得平缓。因此, 当LF> 2.0时并不是线性增加。本文在线性模型的基础上加入指数项, 使得增加趋势变缓, 故该模型虽然较线性模型复杂, 但更符合实际情况, 具有一定的适用性。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 拥挤动态影响系数曲线拟合图Fig.3 Fitting curve of crowding impact coefficient