交通流基本图是表征交通流三参数(流量、速度、密度)之间相关关系的基础模型^[17]。早在1935年, 格林希尔治(Greenshields)^[18]就通过实测机动车交通流数据分析, 提出了第一个速度-密度模型。通过对速度-密度关系模型的建模, 交通流中速度-流量关系模型、流量-密度关系模型也可相应确定。因此, 在机动车交通流中, 主要研究机动车的速度-密度关系模型。梁春岩等^[19]通过实测数据验证了自行车交通流也符合机动车交通流的三参数关系。因此, 本文采用经典的5种机动车交通流速度-密度关系模型进行混合自行车交通流的建模, 其中包括Greenshields模型^[18]、Greenberg模型^[20]、Underwood模型^[21]、Newell模型^[22]以及Pipes-Munjal模型^[23]。各个模型的计算公式如下:

v=vf(1-k/kj)(1)v=vmlog(kj/k)(2)v=vfexp(-k/km)(3)v=vf1-exp-λvf1k-1kj4v=vf1-k/kjn5

式中:v为混合自行车交通流的平均速度; k为混合自行车交通流的密度; v_f为自由流速度; k_j为阻塞密度; v_m为对应通行能力点的最佳速度; k_m为对应通行能力点的最佳密度; λ 、n为待标定参数。

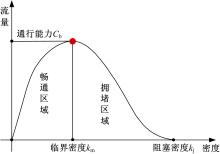
根据交通流理论, 交通流流量-密度关系模型呈现近似如图1所示的形状。在临界密度的左侧, 交通流处于畅通状态, 随着交通流密度的增加, 流量也随之增加。在临界密度的右侧, 交通流处于拥堵状态。这时, 随着密度的增加, 流量会逐渐减少, 直至到达完全阻塞状态。因此, 临界密度将交通状态划分为两类, 其对应的流量点就是该道路的最大流量, 也即道路的通行能力点。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 通行能力计算原理图Fig.1 Theoretic diagram of estimated capacity

v、k满足:

v=q/k6

式中:q为混合自行车交通流的流量。将式(6)带入到式(1)~(5)中, 就可以得到混合自行车交通流的流量-密度关系模型, 即q=f(k)。将其对密度k求导, 导数为零的点即是临界密度点, 进而通过临界密度得到通行能力的估计值。

Cb=fdf(k)dk=07

式中:C_b为自行车道通行能力估计值。

用于自行车道通行能力估计的数据来自于杭州市3个路段的交通调查数据。杭州市以自行车和电动自行车为交通工具出行所占的比例较高, 同时具有比较完善的自行车道系统。3个自行车道的宽度分别为2.4 m、3.0 m和3.5 m, 不存在坡度、弯道等特殊的道路线形形式, 自行车道与机动车道存在物理隔离设施, 与行人道存在植被隔离, 保证自行车侧向不受干扰。数据采集时间为2014年5月21日全天, 天气状况良好, 未发生交通事故等特殊事件。数据采集时间涵盖了高峰、平峰及低峰时间段, 保证交通数据能够涵盖流量-密度曲线的所有取值范围。调查地点为相邻两个交叉口的中间位置断面, 同时远离公交停靠站、行人过街斑马线、出入口等干扰源, 确保自行车数据的可靠性。通过在隐蔽位置架设摄像机记录自行车和电动自行车通过自行车道断面的视频数据。

数据处理分为两部分, 第一部分是通过视频处理软件获取自行车交通流的速度、流量等交通流参数; 第二部分是通过人工手段记录自行车交通流的相关特性参数, 包括自行车类型(普通自行车或电动自行车)、性别(男性或女性)以及年龄(青年、中年或老年), 其中青年为小于30岁, 中年为30~50岁, 老年为50岁以上。

通过数据采集汇总后, 得到如表1所示的相关参数。从表1可以看出, 在车辆类型方面, 电动自行车出行比例超过60%, 占较大比例; 在性别方面, 男性出行者比例较高; 在年龄方面, 青年和中年出行者占绝大部分。

表1

Table 1

表1(Table 1)

表1 自行车调查数据的统计汇总表 Table 1 Statistical description of field bicycle data 路段 路宽 /m 样本量 自行车类型 比例/% 性别比例 /% 年龄比例 /% 路段1 2.4 2944 电动:65.5 普通:34.5 男性:62.7 女性:37.3 青年:50.4 中年:44.3 老年:5.3 路段2 3.0 3252 电动:57.9 普通:42.1 男性:67.3 女性:32.7 青年:54.2 中年:37.9 老年:7.9 路段3 3.5 2885 电动:59.8 普通:40.2 男性:66.3 女性:33.7 青年:51.2 中年:43.3 老年:5.5 合计 (或平均) - 9081 电动:61.0 普通:39.0 男性:65.5 女性:34.5 青年:52.0 中年:41.7 老年:6.3

表1 自行车调查数据的统计汇总表 Table 1 Statistical description of field bicycle data

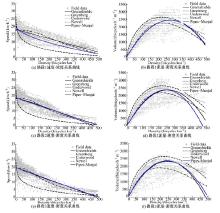
本文采用基于Levenberg-Marquardt(LM)算法进行速度-密度关系模型的参数估计。LM算法是介于牛顿法与梯度下降法之间的一种非线性优化方法, 利用梯度求最大(小)值的算法, 对于过度参数化问题不敏感, 能有效处理冗余参数问题, 使代价函数陷入局部极小值的机会大大减小^[24]。基于LM算法, 使用Matlab软件进行模型曲线拟合与参数估计。交通流参数的统计采样间隔为20 s, 确保存在饱和状态下的自行车流。图2给出了3个路段自行车道速度-密度关系和流量-密度关系的实测散点数据与曲线拟合结果。从图2可以看出, 不同模型的拟合结果不同, 不同地点的估计通行能力也存在一定的差异性。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 速度-密度及流量-密度关系曲线拟合结果Fig.2 Fitting results of speed-density and flow-density relationship curves

表2给出了3个路段5种模型的拟合曲线、估计通行能力与拟合误差。从表2可以看出, 自行车道的自由流速度基本维持在20 km/h左右, 阻塞密度为550~600 辆/km左右。从拟合相对误差来看, 除了Greenberg模型拟合误差较大之外, 其他模型的拟合相对误差基本都在20%以内, 拟合精度相对稳定。从表2给出的通行能力范围来看, 不同模型的通行能力估计结果在2100~2600 辆/(h· m), 存在较大的差异性, 这表明在进行通行能力估计时, 选择合适的模型对结果具有重要的影响。同时, 为了验证不同地点不同车道宽度下的通行能力差异, 采用T检验进行分析, 检验结果(路段1 vs.路段2, p=0.976; 路段1 vs.路段3, p=0.145; 路段2 vs.路段3, p=0.564)表明, 三组T检验结果p值都大于0.05, 即两两路段估计通行能力值之间不存在显著性差异。这也就是说不同自行车道宽度不会对单位通行能力估计值产生显著影响。

表2

Table 2

表2(Table 2)

表2 自行车道通行能力值估计结果与拟合误差 Table 2 Estimated results and fitting errors of bicycle path capacity 模型 路段1 路段2 路段3 平均值 拟合公式 Greenshields v=18.0× (1-k/544) v=18.5× (1-k/513) v=19.6× (1-k/482) Greenberg v=4.7log(578/k) v=4.0log(598/k) v=3.9log(589/k) Underwood v=18.4exp(-k/397) v=18.7exp(-k/382) v=20exp(-k/305) Newell v=17 1-e-(320/k-0.55) v=18 1-e-(280/k-0.47) v=19 1-e-(208/k-0.35) Pipes-Munjal v=18 1-(k/540)1.01 v=18.3 1-(k/475)1.14 v=19.7 1-(k/498)0.92 通行能力 Greenshields 2450 2376 2363 2396 Greenberg 2630 2592 2666 2629 Underwood 2480 2427 2442 2450 Newell 2255 2188 1913 2119 Pipes-Munjal 2449 2379 2325 2384 平均值 2453 2392 2342 2396 拟合误差 Greenshields 19.91% 16.25% 18.17% 18.11% Greenberg 35.20% 32.50% 27.35% 31.68% Underwood 19.90% 16.31% 18.19% 18.13% Newell 20.26% 16.07% 18.65% 18.32% Pipes-Munjal 19.94% 16.08% 18.60% 18.21% 平均值 23.04% 19.44% 20.19% 20.89%

表2 自行车道通行能力值估计结果与拟合误差 Table 2 Estimated results and fitting errors of bicycle path capacity

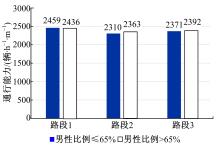
为了验证骑行人性别因素对估计通行能力的影响, 按照男性骑行人比例平均值65%作为分界线, 将所有采集到的速度-密度散点划分为两部分数据, 一部分为男性骑行人比例小于65%的样本散点, 另一部分为男性骑行人比例大于65%的样本散点。分别对两组样本采用LM算法进行非线性参数估计得到模型参数与通行能力估计值。

如图3所示, 图中的通行能力估计值为5种模型估计结果的平均值, 从中可以看出, 3个路段估计的通行能力都不存在显著性差异。男性骑行人的比例大小并没有改变估计通行能力的大小。虽然相关的研究文献表明男性骑行人的速度会大于女性骑行人^[5], 但是却没有对自行车道通行能力产生显著影响。造成这一因素的主要原因是通行能力一般出现在接近饱和状态, 这种状态下交通流较为密集, 所有车辆的速度都趋于一致, 男性与女性骑行人的速度差异也并不明显。同时, 由于电动自行车比例较高, 电动自行车的动力特性较强, 男性与女性在操纵电动自行车时并不存在较大的生理及体力上的差异性。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 不同比例男性骑行人下的估计通行能力Fig.3 Estimated capacity under different proportions of male riders

根据数据采集中对年龄分组(青年、中年或老年)的情况, 将所有采集到的速度-密度散点划分为三部分数据, 第一部分为青年骑行人比例大于70%的样本散点; 第二部分为中年骑行人比例大于70%的样本散点; 第二部分为老年骑行人比例大于70%的样本散点, 分别对三组样本采用LM算法进行非线性参数估计得到模型参数与通行能力估计值。

从表3中可以看出, 所有对比样本的T检验结果表明p值都大于0.05, 即接受原假设, 认为不同年龄骑行者的比例并不会对通行能力造成显著影响。这主要是因为以下两方面的原因:①由于调查路段的出行需求主要是以通勤出行为主, 因此在骑行人年龄构成中, 青年与中年骑行人占主要部分(占到95%左右), 而青年与中年骑行人在人工调查中的区分度并不明显, 同时他们的驾驶技能、反应能力等都相对成熟, 驾驶员差异性也不明显; ②驾驶电动自行车对操控能力要求不高, 年龄因素并不会很大程度上影响骑行人对电动自行车的操控能力, 因而年龄因素对交通流特性的影响较小。因此, 在电动自行车为主导的交通流环境下, 年龄因素并不会对自行车道通行能力产生显著影响。

表3

Table 3

表3(Table 3)

表3 不同年龄比例骑行人下的通行能力T检验结果 Table 3 Results of T test under different proportions of riders’ age 路段 青年 vs 其他 中年 vs 其他 老年 vs 其他 1 均值 2522 2426 2432 2366 2482 2412 标准差 145 231 178 134 198 245 p 0.453 0.943 0.367 H 0 0 0 2 均值 2318 2153 2213 2321 2278 2198 标准差 213 198 254 143 176 190 p 0.560 0.723 0.332 H 0 0 0 3 均值 2325 2499 2387 2345 2354 2301 标准差 213 267 176 190 211 167 p 0.421 0.856 0.287 H 0 0 0

表3 不同年龄比例骑行人下的通行能力T检验结果 Table 3 Results of T test under different proportions of riders’ age

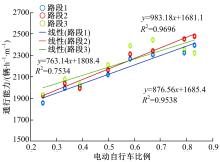
本文将3个路段中20 s采样间隔的速度-密度散点数据按照其中的电动自行车比例分为8组, 每组的电动车比例值为该组数据的平均值。采用LM算法对每组数据进行速度-密度关系曲线的拟合, 从而得到不同电动自行车比例下的估计通行能力值。图4给出了3个路段不同电动自行车比例与自行车道估计通行能力的散点图与线性拟合关系模型。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 不同电动自行车比例下的估计通行能力Fig.4 Estimated capacity under different proportions of electric bicycles

从图4中可以看出, 随着车道电动自行车比例的增加, 估计车道通行能力也随之线性增加。3条路段的相关系数都较高, 具有很好的相关性。通过拟合线性回归模型可以计算得到:在电动自行车比例为零时, 3条路段单位宽度通行能力估计值分别为:1685、1681和1808辆/h; 而当电动自行车比例到达1时, 3条路段单位宽度通行能力估计值分别为2562、2664和2572辆/h, 平均通行能力提升了874辆/h。上述结果表明, 随着电动自行车比例的增加, 单位宽度自行车道的通行能力也会呈线性增加趋势, 自行车道通行能力与电动自行车比例存在显著相关性。造成这一结果的主要原因是电动自行车采用电力驱动, 其运行速度高、运行稳定性强, 导致电动自行车交通流的自由流速度显著大于普通自行车交通流的自由流速度。因此, 电动自行车交通流存在更大的临界速度与临界密度, 从而导致了在交通流基本图中表现为更大的通行能力值。