基于OD分布的环形交叉口车辆行程时间建模

引用本文

宋现敏, 刘焕峰, 李志慧, 陶鹏飞, 杨秋杰. 基于OD分布的环形交叉口车辆行程时间建模. 吉林大学学报: 工学版, 2016, 46(1): 70-75
SONG Xian-min, LIU Huan-feng, LI Zhi-hui, TAO Peng-fei, YANG Qiu-jie. New model of vehicle travel time at roundabout based on OD distribution. Journal of Jilin University Engineering and Technology Edition, 2016, 46(1): 70-75 复制到剪切板

Permissions

基于OD分布的环形交叉口车辆行程时间建模

宋现敏, 刘焕峰, 李志慧, 陶鹏飞, 杨秋杰

吉林大学交通学院,长春 130022

李志慧(1977-),男,副教授,博士.研究方向:交通控制,视频检测.E-mail:lizhih@jlu.edu.cn

作者简介:宋现敏(1978-),女,副教授,博士.研究方向:交通控制,交通流理论.E-mail:songxianmin0708@163.com

基金:国家自然科学基金项目(51278220,51278520); 吉林省科技发展计划重点项目(20130206093SF)

摘要

为直观地反映环形交叉口的车辆拥挤程度,建立了一种基于OD分布的环形交叉口车辆行程时间估计模型。首先针对环形交叉口的特殊性,运用几何知识,建立了无干扰状态下环形交叉口几何尺寸与车辆行程时间的关系模型;其次运用概率统计方法,分析车辆在环形交叉口的车道选择特性,建立了特定OD下的车辆换道次数模型,从而得到车辆由于换道引起的延误时间;然后通过实测数据,分析了交织区断面流量与车辆排队等待时间的关系,建立了车辆在交织区入口处的等待时间模型;最后,运用实测数据对模型进行了参数标定和检验,结果表明,本文模型预测误差在10%以内,满足精度要求。

关键词: 交通运输系统工程; 环形交叉口; 行程时间; 车道选择; 换道行为

中图分类号:U491.1 文献标志码:A 文章编号:1671-5497(2016)01-0070-06

New model of vehicle travel time at roundabout based on OD distribution

SONG Xian-min, LIU Huan-feng, LI Zhi-hui, TAO Peng-fei, YANG Qiu-jie

College of Transportation, Jilin University, Changchun 130022, China

Abstract

In order to directly reflect the degree of congestion at roundabout, a model of vehicle travel time at roundabout was propose based on Origin-Destination (OD) distribution. First for the particularity of roundabout, a relationship model between roundabout geometric dimension and the vehicle travel time under noninterference state was established applying geometric knowledge. Second, probabilistic statistical methods were used to analyze the vehicle's characteristics of lane choosing at roundabout, and a vehicle lane change model was established under specific OD, thus to obtain the vehicle delay caused by lane changing. Third, by analyzing the actual survey data and the relationship between flow rate at weaving section and waiting time, a waiting time model of vehicle at the entrance of weaving area was built. Finally, the model parameters were calibrated and the model was validated using survey data. Results show that the prediction error of the proposed model was within 10% that meets the accuracy requirement.

Keyword: engineering of communication and transportation system; roundabout; travel time; lane choose; lane changing behavior

Show Figures

0 引言

关于行程时间预测方面的研究已持续多年, 主要研究方法分为以下两大类:一类是以数理统计为基础的预测模型^{[1, 2]}; 另一类是以人工智能技术为基础的预测模型^{[3, 4]}。但这些研究多集中在城市道路, 而针对环形交叉口中车辆行程时间预测方面鲜有较成熟的研究。由于环形交叉口的交通流组织形式与典型十字交叉口存在较大差异, 车流在环形交叉口内运行时因相互干扰而产生的延误不可忽略, 故对车辆在环形交叉口的延误进行分析建模是计算环形交叉口车辆行程时间的关键。1962年Tanner等^[5]利用间隙理论提出了无信号交叉口延误模型; Troutbeck^[6]、Akcelik等^[7]在此基础上, 分析了低流量、车流较稳定状况下的环形交叉口车头时距特性, 建立无信号环形交叉口的延误模型。国内一些学者, 从流量角度对环形交叉口内车辆延误情况进行了分析, 郭彩香^[8]将环形交叉口内车辆的延误分为几何延误、交通延误和进口道延误, 分析了环流车流对进口道车辆的延误影响; 王震远^[9]运用仿真方法分析了交通量、交通流向比例、车种组成对平均延误的影响; 东南大学邱荣华、王炜等^{[10, 11]}从自由流比例、饱和度两个角度分析了环形交叉口内的车辆延误。上述研究大多从宏观角度对环形交叉口交通参数进行统计分析, 建立了车辆延误模型, 而在建模过程中忽略了车辆在环形交叉口内换道行为对车辆延误时间的影响。而在换道行为方面, Zheng^[12]分析了多种换道决策模型及换道对周边交通的影响; Guido等^[13]运用概率统计的方法计算环形交叉口的换道概率, 得出换道概率随着可接受车头间距的增加以及相邻车道后车速度的减小而增加, 但上述研究均没有考虑OD对换道次数的影响, 而在环形交叉口中的换道行为是由OD与流量共同决定的。

基于此, 本文将车辆在环形交叉口内的行程时间分为畅行行驶时间、换道引起的延误时间以及在交织区的排队等待时间三部分, 分别分析各部分对环形交叉口内车辆行程时间的影响, 建立环岛内车辆行程时间的计算模型。重点针对换道行为引起的延误, 分析了OD与流量对环形交叉口内车辆换道次数的影响, 建立了换道次数与车辆延误的映射关系。

1 环形交叉口内车辆行程时间建模

1.1 建模思路

车流在环形交叉口内的运行状态直接影响车辆行程时间。当环岛内的车辆以自由流状态行驶, 即车辆间无互相干扰时, 车辆行程时间由其行驶距离与速度决定; 随着环岛内交通流量逐步增大, 交织换道行为频繁发生, 车辆延误亦随之增加; 当环形交叉口流量增大至一定程度时, 进口道入环车流与环道车流在交织区发生严重冲突, 车辆只能排队穿越交汇车流驶出交织区。

本文分别从上述车流的三种状态入手, 首先计算车辆在环形交叉口内以自由流状态行驶时所需的时间, 在此基础上分析由于换道次数带来的延误以及交织区发生排队时所需的等待时间, 综合三部分建立了车流在环形交叉口的行程时间模型。

1.2 假设条件

车辆从进入环形交叉口到驶出环行交叉口是一个比较复杂的过程, 即使同一OD的车辆在环形交叉口内的行驶轨迹也不相同。同一OD的车辆是指:从同一入口进入环形交叉口并从同一出口驶出的车辆。这一OD的车流行驶过程中, 由于环形交叉口结构的特殊性及车辆在环形交叉口内不同的换道行为, 同一OD下的车辆行驶路径可能存在差异, 在本文的研究中假定相同OD的车辆在环形交叉口内的行驶距离是相同的。

1.3 模型建立

根据对行程时间影响因素的分析, 将环形交叉口内车辆行程时间分为畅行行驶时间t₁、换道引起的延误时间t₂以及在交织区入口处的排队等待时间t₃。车辆在环形交叉口内的行程时间为上述三者之和, 如式(1)所示, 下面分别对这三部分进行具体建模。

$\begin{matrix} T = t_{1} + t_{2} + t_{3} (1) \end{matrix}$

1.3.1 畅行行驶时间

环岛内的车辆以自由流行驶时的速度为畅行速度。畅行行驶时间即为车辆行驶距离与畅行速度之比, 如式(2)所示:

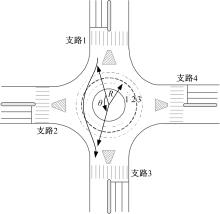
$\begin{matrix} t_{1} = \frac{l}{v} = \frac{θπR}{180 ° \times v} (2) \end{matrix}$

式中:θ 为按车辆行驶方向, 入环支路与出环支路的夹角(° ); R为所有环道宽度的1/2加上环形交叉口半径(m); v为车辆在环形交叉口内的畅行速度(m/s)。

1.3.2 换道引起的延误时间

在环形交叉口中, 个体车辆发生换道时会伴随减速行为, 因此换道行为越频繁, 车辆延误越大。可假定车辆在环形交叉口内的延误时间与换道次数呈线性正比例关系, 即:

$\begin{matrix} t_{2} = f (m) = am (3) \end{matrix}$

式中:m为换道次数; a为待定系数。

在以往的研究中, 通常将换道行为归结为自由换道和强制换道两类, 但在环形交叉口内车辆的换道行为很难确切地划分至上述的某一类型, 同时受限于环岛的尺寸, 自由换道行为发生的频率极少, 因此原有的换道行为分类不适用于环形交叉口。针对环形交叉口内换道行为的特殊性, 将环形交叉口的车辆换道分为以下两类:①入环换道:车辆由入口驶入环形交叉口, 汇入过程中的换道行为。将车辆在环形交叉口中向内侧车道换入的行为均定义为入环换道; ②出环换道:车辆由环形交叉口驶出到支路的过程中的换道行为。将车辆在环形交叉口中向外侧车道换道的行为定义为出环换道。

个体车辆换道次数与其在环形交叉口内的车道选择密切相关。设定环形交叉口环道车道编号从内至外依次为1~n(见图1), 若k为个体车辆穿越整个环形交叉口的过程中所驶入的最内侧车道的编号, 则称该车辆选择第k车道行驶。因此对于单个车辆, 其入环和出环各需换道(n-k+1)次, 则其总换道次数为:

$\begin{matrix} m_{k} = 2 (n - k + 1) (4) \end{matrix}$

式中:m_k为驶入最内侧车道为k的车辆的换道次数, 则该OD下所有车辆的换道次数总和可用下式表示:

$\begin{matrix} m = \overset{n}{\sum_{k = 1}} q_{ij} p_{ij} (k) \times 2 (n - k + 1) (5) \end{matrix}$

式中:q_ij为从第i支路驶入环岛到第j支路驶出环岛的流量, 即路径为i→ j的车辆数; m为路径为i→ j的车辆在环形交叉口内的换道次数; p_ij(k)为q_ij中选择第k条车道行驶的概率。

	Figure Option View Download New Window
	图1 车辆行驶路径与所对应的行驶方向示意图Fig.1 Schematic diagram of vehicle travel path and corresponding angle

关于车道选择特性方面, 已有的研究多是针对高速公路或城市路段的, 研究结果表明车辆的车道选择特性与所在时段的流量有直接关系^{[14, 15]}。环形交叉口不同于普通路段, 车辆在进行车道选择时除了受当时流量的影响外, 还会受自身的目的地的影响。本文对长春市四支环形交叉口(景阳广场)进行实地调查, 通过不同目的地的车辆的车道选择情况分析OD对环形交叉口内车辆车道选择的影响。

表1为由支路1进入环形交叉口, 分别从支路3和4驶出的车辆车道选择比例, 其中车道选择比例为选择各车道的车辆数与该OD下的所有车辆数之比。

表1 支路1进入环形交叉口车流的车道选择比例分析 Table 1 Lane choose proportion analysis of traffic flow from branch one

由表1可得, 环形交叉口的车辆车道选择特性与车辆的OD有密切关系, 因此要获取p_ij(k), 必须在特定的OD下, 分析流量对车道选择的影响。又因环岛内的车辆车道选择行为发生在进入环岛后的第一个交织区与环流区, 交织区由于出环车辆的干扰, 车辆进入目标车道困难, 同时结合车道选择比例与各断面流量的相关性分析结果, 这里的流量选取为车辆入口与出口之间的环流断面的流量q₀, 则在固定的OD下, 假设车道选择概率模型为:

$\begin{matrix} p_{ij} (k) = d_{k} + e_{k} q_{0} (6) \end{matrix}$

式中:d_k、e_k为待定系数, k=1, 2, …, n。

结合式(3)(5)(6), 得到由车辆换道引起的延误时间为:

t₂=a $\begin{matrix} \overset{n}{\sum_{k = 1}} \end{matrix}$ q_ij(d_k+e_kq₀)× 2(n-k+1) (7)

1.3.3 交织区入口处的等待时间

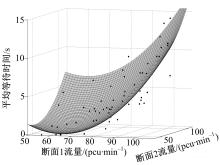
环形交叉口流量增大至一定程度时, 车辆会在交织区发生排队等待现象, 此时排队等待时间由交织区断面流量决定。根据长春市景阳广场实测数据, 统计得到了交织区流量与车辆排队等待时间的关系, 如图2所示。从图2可知车辆等待时间随交织区流量的增大而增加, 且增长趋势与二次曲线相似, 在置信度为95%情况下, R²=0.77。再结合断面个数, 车辆在交织区入口处的等待时间t₃可表示为:

$\begin{matrix} \begin{matrix} t_{3} = f (q_{1}, q_{2}, \dots, q_{i}, \dots, q_{c}) = \\ b_{0} + \overset{c}{\sum_{i = 1}} b_{i} q_{i} + \overset{c}{\sum_{i = 1}} b_{ii} {q_{i}}^{2} + \overset{i < j}{\sum_{i = 1}} b_{ij} q_{i} q_{j} (8) \end{matrix} \end{matrix}$

式中:q_i为交织区断面流量(pcu/min), c为断面个数, i=1, 2, …, c, j=1, 2, …, c; b为待定系数。

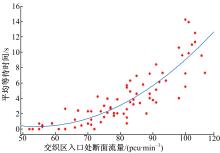	Figure Option View Download New Window
	图2 交织区入口处断面流量与平均等待时间关系Fig.2 Relationship between traffic volume at entrance of weaving area and average waiting time

将式(2)(7)(8)带入式(1), 得到车辆在环形交叉口内的行程时间表达式:

$\begin{matrix} \begin{matrix} T = \frac{θπR}{180 ° \times v} + a \overset{n}{\sum_{k = 1}} q_{ij} (d_{k} + e_{k} q_{0}) \times 2 (n - k + 1) + \\ b_{0} + \overset{c}{\sum_{i = 1}} b_{i} q_{i} + \overset{c}{\sum_{i = 1}} b_{ii} {q_{i}}^{2} + \overset{i < j}{\sum_{i = 1}} b_{ij} q_{i} q_{j} (9) \end{matrix} \end{matrix}$

2 模型验证

2.1 数据获取

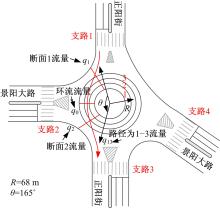
以长春市景阳广场为例, 其中该环形交叉口的几何条件如图3所示。通过在高层建筑物拍摄视频的方式进行数据采集, 运用Corel Video Studio Pro软件进行人工数据提取。提取的数据包括以下三部分:①车辆通过环形交叉口各断面的时刻, 精度为0.04 s; ②车辆在穿过整个环形交叉口的过程中所驶入的最内侧车道编号; ③每分钟环形交叉口各断面的流量。

	Figure Option View Download New Window
	图3 景阳广场示意图Fig.3 Schematic diagram of Jingyang square

对数据①进行初步处理可以得到车辆在各入口处的等待时间以及穿越整个环形交叉口的行程时间; 结合数据②③可以得到车辆在环岛内的车道选择情况以及对应时间段内的环形交叉口环流断面流量。本文主要针对景阳广场从支路1进入环岛到支路3驶出环岛的车辆(即路径为1→ 3的车辆)进行上述所需数据的采集。

2.2 参数标定

对模型中的未知参数进行标定。调查时段为15∶ 00~17∶ 00, 取其中80%数据进行参数标定。按模型建立过程依次计算各部分时间:

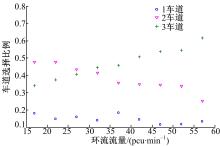
(1)景阳广场如图3所示, v取35 km/h, 测得支路1与支路3之间的夹角约为165° , 由此计算得t₁= $\begin{matrix} \frac{θπR}{180 ° \times v} \end{matrix}$ =20 s。

(2)由式(5)可知, 为计算t₂需获取p_ij(k), 即在路径为1→ 3的情况下车辆选择各车道的比例。统计景阳广场路径为1→ 3的车辆在不同环流流量下的车道选择情况。求解流量相近时的各车道选择比例的平均值, 得第1、第2及第3车道选择比例与环流流量的关系如图4所示。

	Figure Option View Download New Window
	图4 车道选择比例与环流流量关系Fig.4 Relationship between lane choose proportion and circulation flow

由最小二乘法计算拟合出车道选择比例与环流流量的关系式, 得到在观测的流量范围内, 即三环道的环形交叉口, 环流流量在(0~60)pcu/min时路径为1→ 3的车辆选择各车道的比例与环流流量的关系如下所示:

$\begin{matrix} \begin{matrix} p_{13} (3) = - 0.0052 q_{0} + 0.5767, R^{2} = 0.93 \\ p_{13} (2) = 0.0065 q_{0} + 0.2319, R^{2} = 0.98 \\ p_{13} (1) = 1 - p_{13} (2) - p_{13} (3) \end{matrix} \end{matrix}$

将上式带入t₂, 得:

$\begin{matrix} t_{2} = 2 a q_{13} (1.6147 + 0.0039 q_{0}) \end{matrix}$

由调查数据标定参数a, 得a=0.16。

(3)计算拥堵时间t₃, 标定其中的未知参数。以景阳广场路径为1→ 3的车辆为例。由图3可以看出路径为1→ 3的车流在如图所示断面1与断面2, 即交织区入口车流汇入的断面易造成排队等待现象。故调查车辆在交织区入口处的平均等待时间与当时的断面流量, 用MATLAB软件做出散点图, 拟合曲面如图5所示, 在置信度为95%情况下, R²=0.85。

	Figure Option View Download New Window
	图5 断面流量与平均等待时间关系Fig.5 Relationship between sectian flow and average waiting time

t₃=b₀+ $\begin{matrix} \overset{c}{\sum_{i = 1}} \end{matrix}$ b_iq_i+ $\begin{matrix} \overset{c}{\sum_{i = 1}} \end{matrix}$ b_ii $\begin{matrix} {q_{i}}^{2} \end{matrix}$ + $\begin{matrix} \overset{i < j}{\sum_{i = 1}} \end{matrix}$ b_ijq_iq_j=

25.71-0.6761q₁-0.1727q₂+0.0053 $\begin{matrix} q_{1}^{2} \end{matrix}$ +0.00017q₁q₂+0.0016 $\begin{matrix} q_{2}^{2} \end{matrix}$

结合以上三者可得公式中的各参数, 因此车辆在环形交叉口内的行程时间可表示为:

$\begin{matrix} \begin{matrix} T = 20 + 2 \times 0.16 q_{13} (1.6147 + 0.0039 q_{0}) + \\ 25.71 - 0.6761 q_{1} - 0.1727 q_{2} + 0.0053 q_{1}^{2} + \\ 0.00017 q_{1} q_{2} + 0.0016 q_{2}^{2} (10) \end{matrix} \end{matrix}$

2.3 验证

取余下的20%数据作验证, 假设车辆在环形交叉口内的行程时间服从表达式(10), 计算出理论行程时间, 与实际数据作对比, 并分析误差, 结果如图6所示。

	Figure Option View Download New Window
	图6 计算值与实际值对比图Fig.6 Comparison between calculated value and actual value

由公式计算得到的行程时间与实际调查的行程时间最大相对误差为18.11%, 最小相对误差为3.45%, 平均相对误差为8.82%, 在可接受范围内。因此, 该模型预测特定路径下的车辆行程时间具有一定的可靠性。

3 结束语

分析了车辆在环形交叉口内特殊的车道选择行为, 定义了车辆行程时间的三个组成部分, 建立了一种基于OD分布的环形交叉口行程时间预测模型, 并运用实测数据对模型进行了参数标定和检验。结果表明:本文方法预测误差为8.82%, 满足精度要求。该模型预测的车辆行程时间可以直观地反映环形交叉口的道路拥挤程度, 可为环形交叉口信号控制设置提供理论依据。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Kwon J, Coifman B, Bickel P. Day-to-day travel-time trends and travel-time prediction from loop-detector data[J]. Transportation Research Record, 2000, 1717: 120-129. [本文引用:1]
[2]	Rice J, Van Zwet E. A simple and effective method for predicting travel times on freeways[J]. IEEE Transactions on Intelligent Transportation Systems, 2004, 5(3): 200-207. [本文引用:1]
[3]	姚智胜, 邵春福, 熊志华. 支持向量机在路段行程时间预测中的应用研究[J]. 公路交通科技, 2007, 24(9): 96-99. Yao Zhi-sheng, Shao Chun-fu, Xiong Zhi-hua. Research on use of support vector machine for forecasting link travel time[J]. Journal of Highway and Transportation Research and Development, 2007, 24(9): 96-99. [本文引用:1]
[4]	方志伟. 基于浮动车数据的城市路段行程时间预测研究[D]. 北京: 北京交通大学交通运输学院, 2007. Fang Zhi-wei. Prediction study for urban link travel time based on floating-car data[D]. Beijing: School of Traffic and Transportation, Beijing Jiaotong University, 2007. [本文引用:1]
[5]	Tanner J C. A theoretical analysis of delays at an uncontrolled intersection[J]. Biometrika, 1962, 49(1): 163-170. [本文引用:1]
[6]	Troutbeck R J, Kako S. Limited priority merges at unsignalized intersections[J]. Transportation Research Part A: Policy and Practice, 1999, 33(3): 291-304. [本文引用:1]
[7]	Akcelik Rahmi, Edward Chung, Mark Besley. Roundabouts: Capacity and performance analysis[C]//Transportation Research Board Annual Meeting, Washington, DC, USA, 1998. [本文引用:1]
[8]	郭彩香. 城市无信号环形交叉口通行能力及延误研究[D]. 南京: 东南大学交通学院, 2008: 15-19. Guo Cai-xiang. Study on the capacity and delay of no signal roundabout in city[D]. Nanjing: School of Transportation, Southeast University, 2008: 15-19. [本文引用:1]
[9]	王震远. 城市道路环形交叉口车辆排队及行车延误研究[J]. 北京建筑工程学院学报, 2004, 20(3): 54-57. Wang Zhen-yuan. Study on vehicles queuing and delays in roundabout of urban roads[J]. Journal of Beijing Institute of Civil Engineering and Architecture, 2004, 20(3): 54-57. [本文引用:1]
[10]	邱荣华, 李文权. 低渠化环形交叉口延误理论模型研究[J]. 交通运输工程与信息学报, 2005, 3(1): 104-107. Qiu Rong-hua, Li Wen-quan. Study of the delay theory model for low channeling roundabouts[J]. Journal of Transportation Engineering and Information, 2005, 3(1): 104-107. [本文引用:1]
[11]	项乔君, 王炜, 陈冰, 等. 环形交叉口通行能力理论模型研究[J]. 中国公路学报, 1999, 12(4): 69-72. Xiang Qiao-jun, Wang Wei, Chen Bing, et al. A study of the model construction for roundabout's capacity[J]. China Journal of Highway and Transport, 1999, 12(4): 69-72. [本文引用:1]
[12]	Zheng Z. Recent developments and research needs in modeling lane changing[J]. Transportation Research Part B: Methodological, 2014, 60: 16-32. [本文引用:1]
[13]	Guido G, Vitale A. A behavioral lane changing model for roundabout design[C]//The First International Conference on Safety and Security Engineering, Rome, Italy, 2005: 567-575. [本文引用:1]
[14]	张枭雄, 隽志才, 贾洪飞. 不同流量条件下车道利用率的仿真研究[J]. 公路交通科技, 2005, 22(6): 117-120. Zhang Xiao-xiong, Juan Zhi-cai, Jia Hong-fei. Study on the lane utilization ratio under different volumes with microscopic traffic simulation[J]. Journal of Highway and Transportation Research and Development, 2005, 22(6): 117-120. [本文引用:1]
[15]	王晓原, 徐峰. 微观交通仿真研究不同流量条件下的车道利用率[J]. 曲阜师范大学学报: 自然科学版, 2004, 30(4): 15-19. Wang Xiao-yuan, Xu Feng. Study on the lane utilization ratio under different volumes with microscopic traffic simulation[J]. Journal of Qufu Normal University, 2004, 30(4): 15-19. [本文引用:1]

2000

0.0

... 0 引言关于行程时间预测方面的研究已持续多年,主要研究方法分为以下两大类:一类是以数理统计为基础的预测模型^[1,2] ...

2004

0.0

... 0 引言关于行程时间预测方面的研究已持续多年,主要研究方法分为以下两大类:一类是以数理统计为基础的预测模型^[1,2] ...

2007

0.0

. 2007, 24(9):96-99 DOI:doi:10.3969/j.issn.1002-0268.2007.09.022

Research on use of support vector machine for forecasting link travel time

支持向量机在路段行程时间预测中的应用研究

Yao Zhi-sheng , Shao Chun-fu , Xiong Zhi-hua.

姚智胜, 邵春福, 熊志华

Application of theory of support vector machine for forecasting link travel time is discussed.First,link under research is divided into several segments according to locations of traffic flow sensors.Then traffic flows,velocities,lane occupancy rates of these link segments and link travel time in several preceding periods of time are set as input,link travel time in the next period of time is set as output,gauss radial basis function is chosen as kernel function,thus a forecasting model based on support vector machine is presented so as to discuss use of support vector machine for forecasting link travel time.Illustrative numerical tests are conducted using the simulation-based data,where support vector machine and BP neural network are adopted to forecast link travel time,and the errors of these two methods are examined.The result based on support vector machine is superior to that of BP neural network.

主要探讨支持向量机理论在路段行程时间预测中的应用。具体的方法是,首先将研究路段根据路段交通状态和车辆检测器设置情况进行分段,然后以前几个时段的各个小路段的交通流量、平均速度和车道占有率和整个路段的行程时间为输入,以下一时段的整个路段的行程时间为输出,选取高斯径向基函数作为核函数,建立了基于支持向量机的路段行程时间预测模型,从而探讨支持向量机在路段行程时间预测中的应用效果。最后,利用交通仿真软件的模拟数据进行验证,并与BP神经网络计算结果比较,计算结果的对比表明本文提出的方法预测效果更好。

... 另一类是以人工智能技术为基础的预测模型^[3,4] ...

2007

0.0

. 2007, :- DOI:doi:10.7666/d.y1229334

Prediction study for urban link travel time based on floating-car data

基于浮动车数据的城市路段行程时间预测研究[D]

Fang Zhi-wei.

方志伟

随着城市交通状况的持续恶化,人们对实时、准确交通信息的需求更加强烈,而浮动车系统是伴随着ITS新技术应用而发展起来的新型交通信息采集技术,是对传统交通信息采集技术的有益补充。利用浮动车系统数据预测行程时间是ITS领域研究的重要内容,可以为ITS的核心子系统ATIS和ATMS提供实时、准确、可靠的行程时间预测信息,满足系统功能对行程时间预测结果的需求,使其及时采取对策,疏导交通、减少拥挤,以实现交通资源的社会效益与经济效益最大化。本文以城市路段平均行程时间为研究对象,结合实际浮动车行程时间数据,尝试采用新的方法对行程时间进行较为准确的预测。首先介绍了目前较为新颖的浮动车系统交通数据采集系统,阐述了浮动车系统的定义、原理及其采集行程时间数据的过程。其次基于浮动车可以实测路段平均行程时间的基础上,利用基于贝叶斯正则化算法的BP人工神经网络对路段行程时间进行预测。根据不同网络结构、不同样本数据对建立多个预测实例对该方法进行了验证,最后通过遗传算法优化神经网络, 研究进一步提高预测精度的可能性。实验证明结合浮动车数据和BP神经网络的路段行程时间预测结果能满足一定的精度要求,有一定的实用性,而遗传算法优化后的预测精度有了进一步的提高。

... 另一类是以人工智能技术为基础的预测模型^[3,4] ...

1962

0.0

... 1962年Tanner等^[5]利用间隙理论提出了无信号交叉口延误模型 ...

1999

0.0

... Troutbeck^[6]、Akcelik等^[7]在此基础上,分析了低流量、车流较稳定状况下的环形交叉口车头时距特性,建立无信号环形交叉口的延误模型 ...

1998

0.0

... Troutbeck^[6]、Akcelik等^[7]在此基础上,分析了低流量、车流较稳定状况下的环形交叉口车头时距特性,建立无信号环形交叉口的延误模型 ...

2008

0.0

. 2008, :15-19 DOI:doi:10.7666/d.y1244591

Study on the capacity and delay of no signal roundabout in city

城市无信号环形交叉口通行能力及延误研究[D]

Guo Cai-xiang.

郭彩香

随着国家经济的快速发展，道路交通拥堵、交通事故频发和交通环境污染等交通问题也日益严重，交通系统的通行能力成为城市交通系统规划、建设、维护、运营、管理的重要依据。环形交叉口作为城市交叉口的重要组成形式，其交通流特征与常规的公路环形交叉口有很大区别，对城市交通条件下，环形交叉口通行能力和延误的研究，可以有效提高交叉口的交通效率，减少交通事故，进而使整个城市交通问题得到缓解。本文在分析城市环形交叉口通行能力影响因素的基础上，进行实地调研和调查数据分析，根据数据分析结果，主要研究了行人和非机动车干扰条件下，城市环...

... 国内一些学者,从流量角度对环形交叉口内车辆延误情况进行了分析,郭彩香^[8]将环形交叉口内车辆的延误分为几何延误、交通延误和进口道延误,分析了环流车流对进口道车辆的延误影响 ...

2004

0.0

. 2004, 20(3):54-57 DOI:doi:10.3969/j.issn.1004-6011.2004.03.014

Study on vehicles queuing and delays in roundabout of urban roads

城市道路环形交叉口车辆排队及行车延误研究

Wang Zhen-yuan.

王震远

随着国民经济的快速发展,城市机动车保有量持续增加,由此引起了一系列的交通问题.结合北京市东四十条桥环形交叉口的交通状况,采用VISSIM交通微观仿真系统,对环形交叉口车辆排队及行车延误进行了分析研究,得出了车辆排队及延误与通行能力影响因素之间的关系.

... 王震远^[9]运用仿真方法分析了交通量、交通流向比例、车种组成对平均延误的影响 ...

2005

0.0

. 2005, 3(1):104-107 DOI:doi:10.3969/j.issn.1672-4747.2005.01.020

Study of the delay theory model for low channeling roundabouts

低渠化环形交叉口延误理论模型研究

Qiu Rong-hua , Li Wen-quan.

邱荣华, 李文权

研究环形交叉口的延误,用排队论方法分析低渠化环形交叉口的交通流特性,提出环形交叉口通行能力、延误研究的基本思路,建立单向两进口车道与两环行车道的环形交叉口车流延误模型,得出环形交叉口进口道车流延误时间与自由流比例有关;与行车最小车头时距有关;与环形交叉口通行能力有关;与交叉口车流交织段长度有关.模型对环形交叉口的规划、设计以及服务水平的评价具有指导意义.

... 东南大学邱荣华、王炜等^[10,11]从自由流比例、饱和度两个角度分析了环形交叉口内的车辆延误 ...

1999

0.0

. 1999, 12(4):69-72

A study of the model construction for roundabout's capacity

环形交叉口通行能力理论模型研究

Xiang Qiao-jun , Wang Wei , Chen Bing

项乔君, 王炜, 陈冰

对中国国道、省道环形交叉口道路及交通特性进行了分析研究，在此基础上首次以间隙－接受理论建立了适于中国低渠化环形交叉口通行能力的理论模型。

... 东南大学邱荣华、王炜等^[10,11]从自由流比例、饱和度两个角度分析了环形交叉口内的车辆延误 ...

2014

0.0

... 而在换道行为方面,Zheng^[12]分析了多种换道决策模型及换道对周边交通的影响 ...

2005

0.0

... Guido等^[13]运用概率统计的方法计算环形交叉口的换道概率,得出换道概率随着可接受车头间距的增加以及相邻车道后车速度的减小而增加,但上述研究均没有考虑OD对换道次数的影响,而在环形交叉口中的换道行为是由OD与流量共同决定的 ...

2005

0.0

. 2005, 22(6):117-120 DOI:doi:10.3969/j.issn.1002-0268.2005.06.032

Study on the lane utilization ratio under different volumes with microscopic traffic simulation

不同流量条件下车道利用率的仿真研究

Zhang Xiao-xiong , Juan Zhi-cai , Jia Hong-fei.

张枭雄, 隽志才, 贾洪飞

The lane utilization ratio reflects the traffic distribution on different lanes of road section for a single direction.It influences the stability of traffic flow, and is an important influential factor of road capacity and safety.Considering the uncertainty of the lane utilization ratio and the difficulty to collect the field data under different volumes, in this paper, the research is carried out with microscopic traffic simulation model of car-following and lane-changing to study the basic patterns of the lane utilization ratio lane-changing times and the lane utilization ratio traffic volume of the road section with two carriageways or three carriageways.

车道利用率反映的是单一方向路段交通量在不同车道上的分布情况,它影响交通流的稳定性,是道路通行能力和交通安全的重要影响因素。针对不同流量条件下车道利用率的不确定性和现场数据采集困难等特点,应用车辆跟驰、车道变换等微观交通流仿真模型在一体化仿真环境下进行模拟研究,得到双车道和三车道路段流量换道次数以及流量车道利用率关系的基本规律。

... 关于车道选择特性方面,已有的研究多是针对高速公路或城市路段的,研究结果表明车辆的车道选择特性与所在时段的流量有直接关系^[14,15] ...

2004

0.0

. 2004, 30(4):15-19 DOI:doi:10.3969/j.issn.1001-5337.2004.04.004

Study on the lane utilization ratio under different volumes with microscopic traffic simulation

微观交通仿真研究不同流量条件下的车道利用率

Wang Xiao-yuan , Xu Feng.

王晓原, 徐峰

车道利用率反映的是单一方向路段交通量在不同车道上的分布情况,它影响交通流的稳定性,是道路通行能力和交通安全的重要影响因素. 针对不同流量条件下车道利用率的不确定性和难以通过实验采获等特点,应用车辆跟驰、车道变换等微观交通流仿真模型在一体化仿真环境下进行模拟研究,得到双车道和三车道路段流量-换道次数以及流量-车道利用率关系的基本规律.

... 关于车道选择特性方面,已有的研究多是针对高速公路或城市路段的,研究结果表明车辆的车道选择特性与所在时段的流量有直接关系^[14,15] ...