信号交叉口实时排队长度估计

引用本文

赵淑芝, 梁士栋, 马明辉, 刘华胜, 朱永刚. 信号交叉口实时排队长度估计. 吉林大学学报: 工学版, 2016, 46(1): 85-91
ZHAO Shu-zhi, LIANG Shi-dong, MA Ming-hui, LIU Hua-sheng, ZHU Yong-gang. Real-time queue length estimation at signalized intersection. Journal of Jilin University Engineering and Technology Edition, 2016, 46(1): 85-91 复制到剪切板

Permissions

信号交叉口实时排队长度估计

赵淑芝¹, 梁士栋¹, 马明辉¹, 刘华胜¹, 朱永刚²

1.吉林大学交通学院,长春 130022

2.吉林财经大学工商管理学院,长春130117

梁士栋(1990-),男,博士研究生.研究方向:交通运输系统规划.E-mail:liangsd14@mails.jlu.edu.cn

作者简介:赵淑芝(1958-),女,教授,博士生导师.研究方向:交通运输系统规划.E-mail:zhaosz@jlu.edu.cn

基金:国家自然科学基金项目(51378237)

摘要

通过改进的METANET模型来模拟车辆排队形成和释放过程,并以该模型为基础,通过分析排队队尾车辆的空间分布计算得出排队队尾位置,从而获得实时信号交叉口车辆排队长度。最后,对提出的城市信号交叉口排队长度实时估计方法进行验证。结果表明,用本文提出的车辆排队长度估计方法能够实时精确地得到交叉口信号周期内车辆动态排队长度,进而为城市道路交通控制与管理提供必要的决策支持。

关键词: 交通运输工程; 宏观交通流模型; 交叉口信号控制; 排队长度

中图分类号:U491 文献标志码:A 文章编号:1671-5497(2016)01-0085-07

Real-time queue length estimation at signalized intersection

ZHAO Shu-zhi¹, LIANG Shi-dong¹, MA Ming-hui¹, LIU Hua-sheng¹, ZHU Yong-gang²

1.College of Transportation, Jilin University,Changchun 130022,China

2.School of Business Administration,Jilin University of Finance and Economics,Changchun 130117,China

Abstract

In order to estimate the real-time queue length at signalized intersection, a macroscopic traffic flow model METANET was improved to describe vehicle accumulation and discharge process in urban road. First, the queue tail cell is identified according to analysis of the density calculated with the improved traffic flow model. Then, the vehicle spatial distribution in the queue tail cell is analyzed to identify the location of the queue tail, so that the queue length can be calculated. Finally, the proposed model is evaluated and the results demonstrate that this model can be used to estimate queue length in real-time with satisfactory accuracy. The proposed estimation method may be used to support the strategy generation of traffic control and management.

Keyword: communication and transportation engineering; macroscopic traffic flow model; intersection signal control; queue length

Show Figures

0 引言

城市信号交叉口排队长度作为评价城市交通系统运行效率的重要指标, 为城市交通管理与控制提供必要的决策支持^[1]。国内外城市交通相关研究学者针对车辆排队长度的确定问题提出了大量计算方法。现有排队长度估计模型构建主要基于交通波理论、累积曲线理论及排队论方法。累积曲线理论首先由Webster^[2]提出, 通过构建车辆到达与离去曲线, 利用图论的相关方法得到曲线之间的部分, 从而得到排队长度; 交通波理论由Lighthill和Whitham^[3]提出, 用以描述连续交通流, 之后由Stephanopoulos等^[4]和Michalopoulos等^[5]将该理论应用于信号交叉口, 基本原理是通过追踪交通波波阵面的位置得到排队长度; 排队论方法是将道路瓶颈看成一个服务系统, 车辆到达规律服从一定分布, 当车辆到达率超过服务能力时, 排队开始形成, 车辆到达累计数与离去累计数之差为排队车辆数^[6]。目前, 已有的排队长度估计方法主要旨在交通流状态保持不变或连续变化的交通状态条件下, 获得交通交叉口信号周期内最大排队长度^[7]和平均排队长度^[8]。然而, 城市道路交通系统是一个复杂的、随机性极强的系统, 即使在较短时间内, 交通参数也有可能会发生较大的变化, 现有的排队长度估计模型无法对交通流短时变化条件下信号交叉口排队长度进行实时有效地计算。

本文针对城市道路交通流的时变性, 从信号交叉口交通流运行时空特性出发, 对二阶宏观交通流模型METANET进行改进, 使其能够准确有效地对信号交叉口车辆排队形成和消散过程进行描述, 并以此模型为基础, 通过线圈数据实时获取道路上每一个单元内的交通密度, 实时判断排队队尾所在空间单元内的具体位置, 进而构建排队长度估计模型, 以实现对信号交叉口车辆排队长度进行实时有效的估计。

1 二阶宏观交通流模型及扩展

1.1 宏观交通流模型METANET

宏观交通流模型METANET是对交通流动态速度连续守恒方程在时间和空间上实施离散化处理, 实现对交通流在时空域中状态变化的准确描述^[9]。

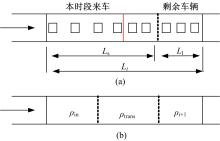
将城市道路两个相邻交叉口所截路段m以长度L_i为单位划分为i个单元, 如图1所示。以单元i为基础对各单元交通流参数变化情况进行描述。根据交通流流量守恒定律, t到t+Δ t采样间隔内, 单元i+1中车辆数等于t时刻单元i车辆加上流入单元i的车辆, 再减去流出单元i的车辆数。每个单元i中流入的交通量q_i(t)等于道路车辆密度ρ _i-₁(t)、车辆平均速度v_i-₁(t)与车道数λ 乘积:

$\begin{matrix} q_{i} (t) = λ \cdot ρ_{i - 1} (t) \cdot v_{i - 1} (t) (1) \end{matrix}$

	Figure Option View Download New Window
	图1 道路离散化示意图Fig.1 Road discretization diagram

对道路交通参数基本关系描述整理可得:

$\begin{matrix} ρ_{i} (t + Δt) = ρ_{i} (t) + \frac{Δt}{λ \cdot L_{i}} (q_{i} (t) - q_{i + 1} (t)) (2) \end{matrix}$

t到t+Δ t采样间隔单元i内动态速度值描述为:t-Δ t到t采样间隔内车辆运行平均速度值同驾驶员期望速度V[ρ _i(t)]离差、q_i(t)引起的速度增加(减少)量及交通流密度对驾驶员经验速度的影响变化量之和, 如式(3)所示:

$\begin{matrix} \begin{matrix} v_{i} (t + Δt) = v_{i} (t) + \frac{T}{τ} \{V [ρ_{i} (t)] - v_{i} (t)\} + \\ \frac{T}{L_{i}} [v_{i - 1} (t) - v_{i} (t)] v_{i} (t) - \\ \frac{λυT}{τ L_{i}} \frac{ρ_{i + 1} (t) - ρ_{i} (t)}{ρ_{i} (t) + κ} (3) \end{matrix} \end{matrix}$

式中:τ 、υ 、κ 均为模型参数, 其中期望速度V[ρ _i(t)]表示为:

$\begin{matrix} V [ρ_{i} (t)] = v_{f} \exp [- \frac{1}{α_{m}} {(\frac{ρ_{i} (t)}{ρ_{c}})}^{α_{m}}] (4) \end{matrix}$

式中:α _m为模型参数; v_f为自由流速度; ρ _c为临界密度。

当交通流处于拥挤状态时, 考虑到下游单元所能容纳的车辆数和道路的通行能力的限制, 单元间的流率应取为上游单元的需求、下游单元的供给与道路通行能力Q_max的最小值:

$\begin{matrix} \begin{matrix} q_{i} (t) = \min {λ ρ_{i} (t) v_{i} (t), λ (ρ_{j} - \\ ρ_{i + 1} (t - Δt)) L_{i}, Q_{\max}} (5) \end{matrix} \end{matrix}$

式(1)~式(5)共同组成宏观交通流基本参数迭代公式, 以此为基础可递推得到路段上任意时刻任一单元内交通基本参数。

1.2 边界单元参数的输入和输出

为了确保路段各个单元格内交通流参数计算的准确性, 除需明确道路内部各单元间传递关系外, 还需对道路整体交通流的输入和输出情况进行描述。

道路交通流输入情况可通过在实验路段起始处设置检测器获得。路段输出交通量主要可通过两种方式获得:①通过布设线圈直接得到输出交通参数^[10]; ②通过信号交叉口的交通信号配时参数对停车线单元格的输出交通参数进行估计。通过信号配时方案对路段输出交通流参数进行估计, 当交通信号为红灯时, 停车线处无车辆通行, 此时单元i+1内交通流密度为零; 当信号灯初变绿灯时, 单元i+1内交通流密度需根据停车线上游单元i内交通流密度及临界密度ρ _c两个基本量确定; 当交通信号处于绿灯初期时, 道路交通流以饱和流率通过停车线, 此时单元i+1内交通流密度为路段临界密度ρ _c; 当信号处于绿灯后期时, 此时如单元i内交通流密度大于临界密度ρ _c, 车流将继续以饱和流率状态通过停车线, 反之, 如小于临界密度ρ _c时, 单元i+1的密度与上一采样间隔内单元i的密度相同。综上, 可以通过信号周期设置情况对边界条件进行确定:

ρ _i+₁(t)= $\begin{matrix} \{\begin{matrix} 0, ift \in redp h ase \\ \min {\frac{q_{i} (t - Δt)}{V_{i} [ρ_{i} (t - Δt)]}, λ \cdot ρ_{c}}, \\ ift \in greenp h ase \end{matrix} \end{matrix}$ (6)

1.3 METANET模型扩展

由于宏观交通流模型METANET最早用于描述高速公路中的连续流, 因此是否能直接将该模型用于描述城市道路信号交叉口前的车辆排队聚散过程, 需要先进行验证。本文利用数值仿真的方法对该模型进行检验。对单车道进行排队长度估计, 时间步长为4 s, 每个单元长度为60 m, 检测器与停车线的距离为480 m(分为8个单元), 首先对一个周期内的到达释放过程进行模拟, 车辆为随机到达, 路段临界密度ρ _c=0.033 veh/(m· lane), 阻塞密度ρ _J=0.144 veh/m。图2为由传统METANET模型计算得到的一个信号周期内各道路各单元格内交通流密度变化示意图, 纵坐标为时间坐标, 横坐标为空间坐标(刻度为单元的编号), 最右侧为停车线, 图例中颜色的深浅代表道路上交通流密度。

	Figure Option View Download New Window
	图2 一个周期排队过程单元格内密度演化Fig.2 Density evolution in a signal cycle

图2可以直观地表现出单元4到单元8中各单元内交通流密度由阻塞密度转化为临界密度过程中所花费的时间不同, 而传统METANET模型假设每个单元具有相同的性质, 除初始和末尾单元外, 剩余单元内交通流密度演变过程应具有一致性, 故假设与检验结果相违背。另一方面, 该离散化交通流模型将每一单元内车辆分布假设为均匀分布, 只要下游单元格内的密度小于阻塞密度就认为能够提供交通供给空间, 故模型描述释放过程中, 单元8尚未达到临界密度时单元7内车辆已经开始移动, 然而实际上单元内车辆分布是不均匀的, 排队释放过程中即使单元内密度低于阻塞密度, 只要单元内最后一辆车没有启动, 上游单元内车辆就不能移动, 即实际交叉口路段车辆排队释放过程中, 路段交通流释放过程应为停车线上游相邻单元8首先以饱和流率释放, 当该单元内交通流密度达到临界密度时, 单元7内车辆开始释放, 依次类推直到交通波传输到排队队尾单元格, 故传统的METANET模型不能直接用于描述城市道路交通变化过程。

针对上述问题, 对METANET模型进行改进, 使其能准确描述城市道路交叉口车辆释放过程。改进思路如下:当下游单元密度均为接近于临界密度, 而该单元格密度等于或接近临界密度时, 与之相邻的上游单元格内车辆开始释放; 反之若该单元格密度尚未达到临界, 则此时相邻上游单元无车辆释放, 具体表示为:

$\begin{matrix} q_{i} (t) = \{\begin{matrix} 0, if ρ_{i - 1} (t - Δt) > ρ_{i} (t - Δt) \\ ρ_{i} (t - Δt) - ρc > ρc; \\ (λ \cdot (2 \cdot ρc - ρ_{i} (t - Δt)) \cdot L_{i}) / Δt, \\ if {ρ_{i}}_{- 1} (t - Δt) > ρ_{i} (t - Δt) \\ 2 \cdot ρc > ρ_{i} (t - Δt) > ρc; \\ \min {λ \cdot ρ_{i} (t) v_{i} (t), Q_{\max}, \\ λ \cdot (ρ_{j} - ρ_{m + 1} (t - Δt)) \cdot L_{i}}, \\ else 。 \end{matrix} (7) \end{matrix}$

2 车辆排队长度估计模型

2.1 排队队尾位置的确定

道路车辆排队形成阶段, 车辆在停车线前不断累积, 此时停车线相邻单元内交通流密度逐渐增加并接近于道路交通阻塞密度, 远离停车线的上游单元车辆呈自由到达状态; 车辆排队释放阶段, 停车线上游单元内车辆以饱和流率依次驶入交叉口, 按照交通流运行方向的反方向, 各单元内交通流密度依次变为临界密度。综上, 队尾单元下游的交通流密度介于临界密度与阻塞密度之间, 其上游单元内交通流密度小于临界密度。

在初步判断排队队尾在单元i或单元i-1中的基础上, 为了能够进一步确定队尾位置, 需对单元i和单元i-1中交通流变化情况进行具体分析。如采样间隔t-Δ t到t内, i-1单元内车辆全部流入单元i内, 说明排队尚未上溯到单元i-1内, 故排队队尾在单元i内; 反之, i-1单元内车辆全部流入单元i内, 说明单元i内已无法提供充足的空间吸收上游车辆, 故此时排队队尾确定在单元i-1中, 排队队尾位置判别条件表示为:

$\begin{matrix} \begin{matrix} 队尾位置 = \\ \{\begin{matrix} i, if q_{i} (t) \cdot Δt \geq λ \cdot ρ_{i - 1} (t - Δt) \cdot L_{i} \\ i - 1, if q_{i} (t) \cdot Δt < λ \cdot ρ_{i - 1} (t - Δt) \cdot L_{i} \end{matrix} (8) \end{matrix} \end{matrix}$

2.2 排队长度估计模型构建

通过对排队队尾位置的初步判别可知排队队尾所处单元, 由于单元长度较长无法得到队尾车辆精确位置, 因此, 需进一步构建精确的排队长度计算模型。根据上文可确认排队队尾所处单元, 对该单元内密度参数进行分析。

图3中, L_s表示单元i为上游来车供给空间长度; L_l为已存车辆占据的空间长度; ρ _in为上游单元车辆进入单元i的车辆密度; ρ _trans为过渡密度; ρ _i+₁为下游单元i+1内交通流密度。结合图3(a)和(b)分析, 单元中排队车辆由上一时段剩余车辆和该时段内到达的车辆共同构成, 而排队队尾与上游到达车辆的密度以临界密度ρ _c为分隔密度, 即当某一位置密度由小于临界密度转变为临界密度时则认为该位置车辆为排队车辆, 故确定排队队尾具体位置只需确定单元内车辆密度分界位置即可。首先对剩余车辆所占据的空间长度L_l进行确定:

$\begin{matrix} \begin{matrix} L_{l} = \frac{n_{i} (t - Δt) - q_{i + 1} (t) \cdot Δt}{λ \cdot ρ_{i + 1} (t)} (9) \\ L_{s} = L_{i} - L_{l} (10) \end{matrix} \end{matrix}$

	Figure Option View Download New Window
	图3 排队队尾单元分析图Fig.3 Analysis of queue tail cell

由于采样间隔时间Δ t较短, 故假设该时间段内车辆呈均匀到达状态, 进而可知图3(b)中ρ _in可表示为:

$\begin{matrix} ρ_{in} = \frac{q_{i} (t - Δt) \cdot Δ t}{λ \cdot L_{i}} (11) \end{matrix}$

采样间隔内新到达的车辆数由单元内密度转变为ρ _trans的车辆和处于自由行驶状态尚未加入车辆排队的车辆组成, 单元供给空间长度和新到车辆数计算如式(12)(13)所示:

$\begin{matrix} \begin{matrix} L_{s} = \frac{n_{x}}{λ \cdot ρ_{in}} + \frac{2 \cdot n_{y}}{λ \cdot (ρ_{in} + ρ_{i + 1} (t))} (12) \\ n_{x} + n_{y} = q_{i} (t - Δt) \cdot Δt (13) \end{matrix} \end{matrix}$

式中:n_x为密度变为ρ _in的车辆数; n_y为密度变为ρ _trans的车辆数。

联立式(12)(13)可解得车辆数n_x:

$\begin{matrix} n_{x} = \frac{λ \cdot ρ_{in} \cdot (ρ_{in} \cdot L_{s} + ρ_{i + 1} (t) \cdot L_{s} - 2 ρ_{i} (t) \cdot Δt)}{ρ_{i + 1} (t) - ρ_{in}} (14) \end{matrix}$

为了进一步确定过渡ρ _trans转变为临界ρ _c排队队尾车辆所处的空间位置, 需对队尾单元空间密度分布情况进行分析, 如图4所示。

	Figure Option View Download New Window
	图4 队尾单元密度空间分布图Fig.4 Spatial distribution of density in queue tail cell

图4中, B点为排队单元内排队队尾所处空间位置, A、B和C点位于同一直线上, 故:

$\begin{matrix} \frac{ρ_{i + 1} (t) - ρ_{in}}{L_{s} - \frac{n_{x}}{λ \cdot ρ_{in}}} = \frac{ρ_{c} - ρ_{in}}{L_{end} - \frac{n_{x}}{λ \cdot ρ_{in}}} (15) \end{matrix}$

整理式(15)得到单元内排队队尾位置L_end:

$\begin{matrix} \begin{matrix} L_{end} = \frac{2 λ \cdot n_{y} \cdot ρ_{in} \cdot (ρ_{c} - ρ_{in})}{ρ_{in} \cdot (ρ_{i + 1}^{2} (t) - ρ_{in}^{2})} + \\ \frac{λ \cdot n_{x} \cdot (ρ_{i + 1}^{2} (t) - ρ_{in}^{2})}{ρ_{in} \cdot (ρ_{i + 1}^{2} (t) - ρ_{in}^{2})} (16) \end{matrix} \end{matrix}$

队尾位置计算公式存在分母可能为零值情况, 需对分母为零时排队长度的计算方法进一步讨论:

(1)当ρ _i+₁(t)=0时, 交叉口信号处于红灯启亮初期, 交叉口排队刚刚开始, 排队队尾临近停车线单元, 停车线下游虚拟单元格密度为0, 此时ρ _i+₁(t)不能作为末尾单元格密度, 可由阻塞密度ρ _j替换, 排队队尾位置L_end可表示为:

$\begin{matrix} L_{end} = \frac{2 λ \cdot n_{y} \cdot ρ_{in} \cdot (ρ_{c} - ρ_{in}) + λ \cdot n_{x} \cdot (ρ_{j}^{2} - ρ_{in}^{2})}{ρ_{in} \cdot (ρ_{j}^{2} - ρ_{in}^{2})} (17) \end{matrix}$

(2)当ρ _in=0时, 此种情况的物理意义是本时段排队队尾单元i内无车辆驶入, 故判断排队队尾应位于上一时段该单元剩余车辆队尾位置, 即:

$\begin{matrix} L_{end} = L_{i} - L_{l} = L_{i} - \frac{n_{i} (t - Δt) - q_{i + 1} (t) \cdot Δt}{λ \cdot ρ_{i + 1} (t)} (18) \end{matrix}$

(3)当 $\begin{matrix} ρ_{i + 1}^{2} \end{matrix}$ (t)- $\begin{matrix} ρ_{in}^{2} \end{matrix}$ =0时, 由于密度参数为非负, 根据上文排队队尾初步判别方法可知排队队尾单元格上有单元密度ρ _i-₁(t)小于临界密度ρ _c、而下游相邻单元格密度ρ _i+₁(t)应大于临界密度ρ _c, 则有ρ _i+₁(t)=ρ _in=ρ _c, 本时段进入队尾单元的车辆全部加入排队, 排队队尾位于单元末端, 则有L_end=0。

综上对排队单元内排队队尾位置L_end进行了确定, 以此为基础对交叉口排队长度L_q进行计算, 排队长度为队尾单元内排队长度与下游所有单元长度之和, 如式(19)所示:

$\begin{matrix} L_{q} (t) = L_{i} - L_{end} + \overset{I}{\sum_{j = i + 1}} L_{i} (19) \end{matrix}$

第k个信号周期内交叉口平均排队长度为该周期内所有的采样时刻排队长度的算术平均值, 即:

$\begin{matrix} \begin{matrix} L_{K, average} = \\ \frac{L_{q} (\frac{KC}{Δt}) + L_{q} (\frac{KC}{Δt} + 1) + \dots + L_{q} (\frac{(K + 1) C}{Δt})}{C / Δt} (20) \end{matrix} \end{matrix}$

第k个周期内最大排队长度为该周期内所有的采样时刻排队长度的最大值, 即:

$\begin{matrix} \begin{matrix} L_{K, \max} = \\ \max {L_{q} (\frac{KC}{Δt}), L_{q} (\frac{KC}{Δt} + 1), \dots, L_{q} (\frac{(K + 1) C}{Δt})} (21) \end{matrix} \end{matrix}$

3 实证分析

3.1 实验方案设计

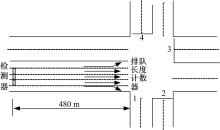
根据本文所提出的城市路段车辆排队长度计算方法对交叉口排队长度计算流程进行描述, 首先利用交通流模型得到道路上车辆空间分布, 进而根据道路上各单元内交通流密度获得车辆排队队尾所在单元, 最后根据队尾单元格内密度分布情况计算得出排队队尾确切位置。为了提高仿真数据与实际交通流运行数据的契合度, 选用长春市某交叉口作为仿真拟合区域, 并通过在该区域采集的交通流数据对VISSIM仿真软件相关参数进行标定。利用VISSIM仿真软件对本文提出的排队长度估计模型进行仿真验证, 交叉口示意如图5所示。

	Figure Option View Download New Window
	图5 仿真交叉口示意图Fig.5 Intersection for simulation platform

仿真软件基本参数设置如下:在瓶颈区域起始路段起点处布设检测器, 天气状况良好, 仿真路段总长度为480 m, 以60 m为基本单位将仿真路段划分为8个单元, 采样间隔为4 s, 自由流速度为15 m/s, 对进口道1的三条直行车道上的排队长度进行估计, 采用仿真软件中Wiedeman 74跟驰模型, 并将车辆驾驶行为设置为通过检测器后不再发生换道行为, 为了对各种状态下排队长度进行有效估计, 输入流量由小逐渐变大设置, 东西直交叉口、东西左交叉口、南北直交叉口、南北左交叉口的绿灯时长分别为68、40、48、36 s。

3.2 实验结果分析

通过VISSIM仿真软件对交叉口进口道1的交通运行态势进行仿真, 获得道路交通运行基本参数数据, 并通过本文提出的排队长度计算方法对周期内道路的最大排队长度和平均排队长度进行计算, 并与通过传统METANET计算得出的排队长度以及仿真输出的实际道路车辆排队长度进行对比分析。

为了详细说明改进后交通流密度模型的有效性和本文提出城市道路排队长度实时计算模型的具体实施过程, 以改进后交通流模型计算得出的一个周期内路段上各个单元内交通流密度演化过程为例, 以密度图形式进行展现, 如图6所示。为了能够直观表现出改进前后的差别, 参数设置与图2一致。

	Figure Option View Download New Window
	图6 基于改进模型的密度演化过程Fig.6 Density evolution based on modified METANET

结合图2和图6对比改进前、后交通流模型对单元密度变化过程的描述。图2中, 在排队释放过程中, 随时间变化, 每一个单元内密度变化过程存在一定的差异性, 即越靠近停车线位置的元胞密度变化越快, 而越远离停车线的单元内元胞密度变化越慢, 与其模型假设各单元内同质性相矛盾, 同时, 与实际排队释放过程也存在一定差异, 由改进后模型计算获得的各单元内交通流密度变化呈现出相同的演变规律, 故原有模型中存在的密度变化不均匀现象(如图2所示)通过模型改进得到了有效解决, 且改进后模型能够准确体现实际排队释放过程中道路各单元内交通流密度的演变过程。

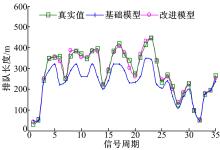
由图7可以看出, 仿真初期由于道路运行车辆数较少, 仿真路段基本无车辆排队产生, 但随着道路交通流量的增加, 车辆排队产生, 图7中3条曲线所呈现的车辆排队变化趋势基本一致。通过本文提出的排队长度计算模型计算得出的车辆最大排队长度曲线同仿真得出的实际最大排队长度曲线基本重合, 而通过未改进模型获得的计算值比真实值小。

	Figure Option View Download New Window
	图7 最大排队长度计算结果对比Fig.7 Comparison of maximum queue length estimation

改进后模型计算得出的最大排队相对误差值基本在5%左右波动, 平均相对误差为4.17%, 平均绝对误差为10 m; 而未改进模型计算结果相对误差大约在20%上下波动, 平均相对误差为17.2%, 平均绝对误差为41 m, 说明与传统模型相比, 改进后模型能够准确地计算得到车辆的最大排队长度。由此可以看出, 改进模型能较为准确地对道路交通流的最大排队长度进行计算, 且计算结果的相对误差处在容忍度(0~5%)以内。

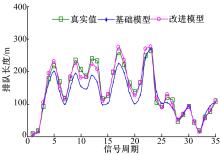
由图8可知, 传统METANET模型计算出的车辆平均排队长度低于真实值, 这是由于应用该原始模型时, 队尾单元内的车辆会比实际中提前移动, 导致本应加入排队的车辆没有减速停车而是直接以较大速度向前行驶, 因此排队车辆较实际排队车辆较少, 该结果与第一节中的分析相吻合。而改进模型平均排队长度计算值同真实值具有较高的吻合度。改进模型平均排队长度相对误差值波动较小, 误差范围在16%以内, 平均误差为7.04%, 平均绝对值为8 m; 而传统模型平均排队长度相对误差值波动较大, 平均误差为15.53%, 绝对误差平均值为18 m。由此可知, 相对于传统模型构建的排队长度计算模型, 改进模型能够更加精确地计算出车辆排队长度值, 且与排队长度实际采样值具有较好的契合度。

	Figure Option View Download New Window
	图8 平均排队长度计算结果Fig.8 Comparison of average queue length estimation

4 结束语

针对城市道路交叉口上游车辆排队长度难以精确测量等问题, 提出对宏观交通流模型METANET进行改进, 以再现交叉口处车辆排队形成、消散过程, 并以此为基础, 从交叉口排队动态变化时空特性角度出发, 对车辆排队形成过程进行深入分析, 从而构建实时排队长度计算模型, 并通过仿真手段验证了该模型的有效性和排队长度计算精确性, 进而为城市交叉口管理与控制提供了实时可靠的决策依据。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Mirchand ani P B, Zou N. Queuing models for analysis of traffic adaptive signal control[J]. IEEE Transactions on Intelligent Transportation Systems, 2007, 8(1): 50-59. [本文引用:1]
[2]	Webster F V. Traffic signal settings[J]. Road Research Laboratory Technical Paper, 1958, 39(1) , 1-39. [本文引用:1]
[3]	Lighthill M J, Whitham G B. On kinematic waves. II. a theory of traffic flow on long crowded roads[J]. Proceedings of the Royal Society of London, Series A: Mathematical and Physical Sciences, 1955, 229(1178): 317-345. [本文引用:1]
[4]	Stephanopoulos G, Michalopoulos P G, Stephanopoulos G. Modelling and analysis of traffic queue dynamics at signalized intersections[J]. Transportation Research Part A: General, 1979, 13(5): 295-307. [本文引用:1]
[5]	Michalopoulos P G, Stephanopoulos G, Stephanopoulos G. An application of shock wave theory to traffic signal control[J]. Transportation Research Part B: Methodological, 1981, 15(1): 35-51. [本文引用:1]
[6]	Newell G F. Applications of Queuing Theory[M]. Cambridge: University Press, 1982. [本文引用:1]
[7]	祁宏生, 王殿海. 信号控制交叉路口车辆排队长度[J]. 吉林大学学报: 工学版, 2009, 39(6): 1457-1462. Qi Hong-sheng, Wang Dian-hai. Vehicle queue length at signal controlled intersection[J]. Journal of Jilin University(Engineering and Technology Edition), 2009, 39(6): 1457-1462. [本文引用:1]
[8]	姚荣涵, 贾婧. 单车道路段上车辆排队的链式反应模型[J]. 吉林大学学报: 工学版, 2012, 42(4): 892-898. Yao Rong-han, Jia Jing. Chain reaction models for vehicles queuing on signal-lane road section[J]. Journal of Jilin University(Engineering and Technology Edition), 2012, 42(4): 892-898. [本文引用:1]
[9]	Kotsialos A, Papageorgiou M, Mangeas M, et al. Coordinated and integrated control of motorway networks via non-linear optimal control[J]. Transportation Research Part C: Emerging Technologies, 2002, 10(1): 65-84. [本文引用:1]
[10]	杨庆芳, 马明辉, 杨聚芬, 等. 高速公路交通流运行稳定性分析[J]. 吉林大学学报: 工学版, 2014, 44(6): 1596-1603. Yang Qing-fang, Ma Ming-hui, Yang Ju-fen, et al. Analysis of the traffic flow operating stability on highway[J]. Journal of Jilin University(Engineering and Technology Edition), 2014, 44(6): 1596-1603. [本文引用:1]

2007

0.0

... 0 引言城市信号交叉口排队长度作为评价城市交通系统运行效率的重要指标,为城市交通管理与控制提供必要的决策支持^[1] ...

1958

0.0

... 累积曲线理论首先由Webster^[2]提出,通过构建车辆到达与离去曲线,利用图论的相关方法得到曲线之间的部分,从而得到排队长度 ...

1955

0.0

... 交通波理论由Lighthill和Whitham^[3]提出,用以描述连续交通流,之后由Stephanopoulos等^[4]和Michalopoulos等^[5]将该理论应用于信号交叉口,基本原理是通过追踪交通波波阵面的位置得到排队长度 ...

1979

0.0

1981

0.0

1982

0.0

... 排队论方法是将道路瓶颈看成一个服务系统,车辆到达规律服从一定分布,当车辆到达率超过服务能力时,排队开始形成,车辆到达累计数与离去累计数之差为排队车辆数^[6] ...

2009

0.0

. 2009, 39(6):1457-1462

Vehicle queue length at signal controlled intersection

信号控制交叉路口车辆排队长度

Qi Hong-sheng , Wang Dian-hai.

祁宏生, 王殿海

A study was performed to estimate the real-time vehicle queue length before the stop line at the urban signal controlled intersection. The relationship among traffic flow directions in road sections was analyzed, and two models,i.e., an artificial neural network model and a Bayesian network model were established to deal with the effects of traffic flows in the road sections, and the structure of the models was specified. To facilitate the practical application of these models, the principal component analysis was used to decrease the input dimensions, the EM algorithm and GMM were used to represent the parameters of the train models. A simulation road network was designed based on the real world data to validate the proposed models under various experiment scenarios. Simulation results showed that the Bayesian network model can grasp the traffic flow tendencies better than the artificial neural network model because of the randomness in the urban road network.

建立了一个能够估计市内信号交叉路口车辆实时排队长度的模型。分析了路段交通流之间的流向关系，根据流向关系建立了两种路段交通流影响模型：神经网络模型和贝叶斯网络模型，并描述了模型的结构。为了方便模型的实际应用，分别用主成份对输入变量降维，用EM算法和高斯混合分布函数来表达模型和训练模型参数。基于实际路网设计了一个仿真路网，并用不同的实验场景对模型进行有效性验证。仿真实验的结果表明，由于城市路网中存在的随机性，贝叶斯网络模型能够更好地把握交通流变化的趋势。

... 目前,已有的排队长度估计方法主要旨在交通流状态保持不变或连续变化的交通状态条件下,获得交通交叉口信号周期内最大排队长度^[7]和平均排队长度^[8] ...

2012

0.0

. 2012, 42(4):892-898

Chain reaction models for vehicles queuing on signal-lane road section

单车道路段上车辆排队的链式反应模型

Yao Rong-han , Jia Jing.

姚荣涵, 贾婧

To reveal the vehicle queue formation and dissipation behavior on a road section with a single lane, the similarity between the growth and dissipation process of vehicle queuing and the chain reaction process of nuclear fission was described. According to the theory of nuclear chain reaction, a chain reaction model system of vehicle queuing on a road section with a single lane was built, including the vehicle queue formation model, the vehicle queue dissipation model, and the vehicle queue model for signalized intersections. By using the field survey data from a typical road section in Dalian city, vehicle queue formation and dissipation models were validated. Also, the numerical simulations for traffic streams under different conditions were made by applying MATLAB software. Based on the simulation results, the sensitivities of the propagation speed of block and dissipation signal to arrival flow rate and running speed were further analyzed. The results show that the proposed models were characterized by high precision, which can be used to calculate the propagation velocity and boundary of the chain reaction of vehicle queuing, and explain the vehicle queue behavior on a road section with a single lane. The research achievements provide a foundation for explaining the vehicle queuing behavior on a multilane road section and the chain reaction mechanism of road jam, give a theoretical basis for solving urban traffic congestion and jam problems and offer a novel idea and a method for studying traffic queue.

为揭示单车道路段上车辆排队的演化规律,描述了车辆排队的形成和消散过程与核裂变的链式反应过程之间的相似性。根据核链式反应原理,建立了单车道路段上车辆排队的链式反应模型体系,包括车辆排队形成模型、车辆排队消散模型和信号交叉口车辆排队模型。利用大连市典型路段的实测交通数据对车辆排队形成和消散模型进行了验证,并运用MATLAB软件对不同条件下的交通流进行数值模拟,分析了阻滞信号和消散信号的传播速度对于到达流量和行驶速度的敏感度。结果显示,模型具有较高的精度,可以测算单车道路段上车辆排队的链式反应速度和范围,能够解释车辆排队形成和消散的内在规律。研究成果为解析多车道路段上车辆排队的演化规律以及路段阻塞的链式反应规律奠定了基础,可为解决城市交通拥堵问题提供理论依据,同时为研究交通排队提供新的思路和方法。

2002

0.0

... 1 宏观交通流模型METANET宏观交通流模型METANET是对交通流动态速度连续守恒方程在时间和空间上实施离散化处理,实现对交通流在时空域中状态变化的准确描述^[9] ...

2014

0.0

. 2014, 44(6):1596-1603 DOI:doi:10.13229/j.cnki.jdxbgxb201406010

Analysis of the traffic flow operating stability on highway

高速公路交通流运行稳定性分析

Yang Qing-fang , Ma Ming-hui , Yang Ju-fen

杨庆芳, 马明辉, 杨聚芬

In order to enhance the credibility of the highway speed limit setting and ensure reasonable selection of speed control method, this paper analyzes the traffic flow data collected by single section and double section. The analysis is from the perspective of spatial and temporal characteristics of highway. Then three stability analysis models are constructed, which treat speed difference as the main research focus. Further, a recognition method of traffic flow stability is presented. The three new models are verified with the microwave monitoring data on a highway in Shandong province using WISSIM simulation software. The results show that identification model of traffic flow stability can identify the dispersion of traffic flow and describe the stability of traffic flow efficiently, which will provide reliable decision basis for highway management of dynamic speed limits.

为了提升高速公路限速值设置的可信度,确保速度控制方法选择的合理性,从高速公路交通流运行的时间特性和空间特性角度出发,对单截面和双截面采集的交通流参数数据进行分析,分别构建了以速度差为基础的稳定性分析模型,并进行优化组合,提出了高速公路交通流稳定性识别方法。采用山东某高速公路微波实测数据和VISSIM微观仿真软件对其进行实证分析,结果表明:高速公路交通流稳定性识别方法能够高效地识别出道路交通流的离散度,并能够定量地、较好地描述交通流运行的稳定性,从而为高速公路的动态限速管理及限速值的确定提供可靠的决策依据。

... 路段输出交通量主要可通过两种方式获得:①通过布设线圈直接得到输出交通参数^[10] ...