信号控制交叉口车均延误模型适用性分析

引用本文

姚荣涵, 刘美妮, 徐洪峰. 信号控制交叉口车均延误模型适用性分析.吉林大学学报:工学版, 2016, 46(2): 390-398
YAO Rong-han, LIU Mei-ni, XU Hong-feng. Applicability analysis of vehicle delay models for isolated signalized intersection. Journal of Jilin University Engineering and Technology Edition, 2016, 46(2): 390-398 复制到剪切板

Permissions

信号控制交叉口车均延误模型适用性分析

姚荣涵, 刘美妮, 徐洪峰

大连理工大学交通运输学院,辽宁大连 116024

通讯作者:徐洪峰(1978-),男,副教授,博士.研究方向:交通组织,管理与控制.E-mail:hfxu@dlut.edu.cn

作者简介:姚荣涵(1979-),女,副教授,博士.研究方向:交通流理论,交通控制,交通规划.E-mail:cyanyrh@dlut.edu.cn

基金:国家自然科学基金项目(61374193); 教育部人文社会科学研究青年基金项目(13YJCZH213)

摘要

构建一种基于一定交通需求和信号控制的实验环境,对比分析了4种经典的信号控制交叉口车均延误模型的适用性.首先,从模型结构和变量个数两个角度比较了4种车均延误模型在使用过程中的难易程度.然后,针对微观交通仿真软件VISSIM,研究了检测区段和分析期对延误测算值的影响.最后,通过对交叉口饱和度与周期时长进行交叉分类设计了多种实验方案,进而对比分析了4种车均延误模型与仿真模型的吻合程度.结果显示,Webster模型简单易用,倾向于低估延误,其适用性最差;ARRB模型较为复杂,其适用性最好;HCM1985模型同样简单易用,其适用性一般;HCM2000模型适用范围广但过于复杂,其适用性一般.总体来讲,对于单点信号控制交叉口,ARRB车均延误模型在估计车辆延误方面有最好的性能表现.本文研究成果能为选用车均延误模型提供理论依据与参考.

关键词: 交通运输系统工程; 车均延误模型; 难易程度; 适用性

中图分类号:U491.2 文献标志码:A 文章编号:1671-5497(2016)02-0390-09

Applicability analysis of vehicle delay models for isolated signalized intersection

YAO Rong-han, LIU Mei-ni, XU Hong-feng

School of Transportation and Logistics, Dalian University of Technology, Dalian 116024, China

Abstract

To analyze the applicability of four vehicle delay models for signalized intersections, the experimental environments were designed on the basis of certain traffic demands and signal control. First, the degree of difficulty for using the four vehicle delay models was compared in view of model structure and the number of variables. Then, for the microscopic traffic simulation software VISSIM, the impacts of the travel time section and analysis duration on the measured delay were discussed. Finally, several experimental scenarios were designed according to the cross-classification of the intersection degree of saturation and cycle length. The goodness of fit between each vehicle delay model and the simulation model was investigated. Results show that the Webster model is easy to use and apt to underestimate vehicle delay and its applicability is the worst; the ARRB model is more complex and its applicability is the best; the HCM1985 model is also easy to use and it applicability is moderate; the HCM2000 model has broad application range but it is too complex, and its applicability is moderate. On the whole, for isolated signalized intersections, the ARRB model displays the best performance in vehicle delay estimation. This research may provide a theoretical basis and reference to the selection of vehicle delay model.

Keyword: engineering of communications and transportation system; vehicle delay model; degree of difficulty; applicability

Show Figures

0 引言

车辆延误是指机动车通过某一道路区段的实际行程时间与理想行程时间的差值.就信号控制交叉口而言, 某一控制时段内, 通过各个机动车相位的行程时间检测区段的所有机动车的车辆延误算术平均值称为车均延误.车均延误能够表征信号控制交叉口的通行效率和服务水平, 获取车均延误是科学制定交通管理与控制技术方案, 客观评价交通管理与控制技术方案性能表现的重要依据.鉴于车辆延误受到诸多因素的影响, 现实中, 通过人工调查方法获取车均延误是一项十分艰巨的工作.基于交通流理论, 排队论的经典方法建立的车均延误模型, 能够以较小的代价估计信号控制交叉口的车均延误, 在交通管理与控制理论, 方法和关键技术的研究中起到重要作用.

目前, 受到业界广泛认同的车均延误模型包括Webster模型^[1], ARRB模型^[2], HCM1985模型^[3]和HCM2000模型^[4].众多研究者致力于修正上述模型, 以便适应更为丰富, 多样的应用场景, 并提高车均延误估计的精确度和可靠度.针对不均衡交通情况, Arasan等^[5]通过考虑不同车辆组之间的交互作用采用一次二阶矩概率方法估计了信号交叉口的车辆延误.沈旅欧等^[6]通过实例分析了基于车道组和基于车道的两种控制延误计算方法的适用条件.针对利用请求检测器和连续相位的半感应和全感应控制, Lin等^[7]基于修正的韦伯斯特模型提出了用于评价替代配时方案的延误模型.为了清楚地理解溢出排队, van Zuylen等^[8]运用描述排队长度概率分布的马尔科夫链模型分析了交叉口的延误计算问题, 进而针对定时交通控制导出了新的延误公式.为使延误模型能准确地估计特定场景下的车辆延误, 庄焰等^[9]利用中国的实际调查数据采用最小二乘法修正了HCM2000延误模型; Akgü ngö r^[10]通过将延误参数作为分析期的函数而非固定值提出了一种新的信号交叉口延误模型, 并与现有的4种延误模型进行了性能对比; Mazloumi等^[11]通过考虑驾驶员行为提出了一种适用于交通分配模型的延误函数.针对孤立, 定时控制交叉口, Chen等^[12]提出了一种延误可变性分析模型, 研究了饱和度和到达规律对延误可变性的影响.针对欠饱和与过饱和情况, Dion等^[13]比较了确定性排队模型, 冲击波模型, 韦伯斯特稳态模型以及1981年澳大利亚通行能力指南, 1995年加拿大通行能力指南, 1994和1997版通行能力手册定义的排队模型与INTEGRATION微观交通仿真软件对延误估计的结果.此外, 微观交通仿真软件VISSIM以单个车辆为研究对象, 通过模拟车辆的运行轨迹可以准确地获取每条车道或车道组上单个车辆的延误数据, 并进而集计成进口道或交叉口的延误数据^[14].

虽然信号控制交叉口车均延误模型已得到很大发展, 但是这些模型的延误计算值能否准确地反映实际的延误, 哪种模型的适用性更好, 在以后的研究中应选择哪种模型作为评价标准, 这些问题仍需进一步探讨.鉴于此, 本文选择4种得到业界广泛认同的车均延误模型来进行分析, 比较各模型在使用过程中的难易程度, 并构建了一种基于一定交通需求和信号控制的实验环境, 对比延误模型的计算结果与VISSIM仿真模型的实验结果, 进而评价各延误模型的适用性.

1 车均延误模型

根据交通流运行特性和延误成因, 信号控制交叉口的车辆延误可分为均匀延误, 随机延误与过饱和延误, 后两者又被统称为增量延误.均匀延误反映交通流的流体特性, 可由流体理论来描述; 增量延误代表交通流的随机性, 可用排队模型来刻画.现有的车均延误模型采用不同的思路和方法对车辆延误进行估计, 其侧重点与适用性各不相同.本文分析以下4种经典的车均延误模型.

1.1 Webster延误模型

1958年, Webster^[1]在假设车辆到达服从泊松分布的基础上, 通过修正给出的车均延误模型为:

$\begin{matrix} d_{i} = 0.9 [\frac{C (1 - λ_{i})^{2}}{2 (1 - λ_{i} x_{i})} + \frac{{x_{i}}^{2}}{2 q_{i} (1 - x_{i})}] \end{matrix}$ (1)

式中:λ _i=g_i/C; g_i=G_i-l_s+e; x_i=q_i/c_i; c_i=S_iλ _i; d_i为车道组i的车均延误(s/pcu); C为信号周期时长(s); λ _i为车道组i的绿信比; g_i为车道组i的有效绿灯时间(s); G_i为车道组i的显示绿灯时间(s); l_s为前损失时间(s); e为后补偿时间(s); x_i为车道组i的饱和度; q_i为车道组i的交通量(pcu/h); c_i为车道组i的通行能力(pcu/h); S_i为车道组i的饱和流率(pcu/h).

1.2 ARRB延误模型

1981年, Akç elik^[2]基于稳态理论提出车均延误模型, 该模型也被称为ARRB模型:

$\begin{matrix} d_{i} = \{\begin{matrix} \frac{C (1 - λ_{i})^{2}}{2 (1 - y_{i})} + \frac{c_{i} x_{i} T}{4 q_{i}} [(x_{i} - 1) + \frac{}{} \\ \sqrt[]{(x_{i} {- 1)}^{2} + \frac{12 (x_{i} - x_{0 i})}{c_{i} T}}], x_{i} > x_{0 i} \\ \frac{C (1 - λ_{i})^{2}}{2 (1 - y_{i})}, x_{i} \leq x_{0 i} \end{matrix} \end{matrix}$ (2)

式中:y_i为车道组i的流量比, y_i=q_i/S_i; x₀_i为平均溢出排队近似为0时车道组i的饱和度, x₀_i=0.67+S_ig_i/600; T为分析期(h).

1.3 HCM1985延误模型

1985年, 美国通行能力手册(HCM)在假设车辆随机到达的基础上, 利用协调变换方法得到的车均延误模型^[3]为:

$\begin{matrix} \begin{matrix} d_{i} = \frac{0.38 C (1 - λ_{i})^{2}}{(1 - λ_{i} x_{i})} + 173 {x_{i}}^{2} [(x_{i} - 1) + \\ \sqrt[]{(x_{i} {- 1)}^{2} + 16 x_{i} / c_{i}}] \end{matrix} \end{matrix}$ (3)

1.4 HCM2000延误模型

2000年, 美国通行能力手册(HCM)将车均延误模型修正为^[4]:

$\begin{matrix} \begin{matrix} d_{i} = \frac{0.5 C (1 - λ_{i})^{2}}{1 - \min (1, x_{i}) λ_{i}} \times \frac{(1 - P_{i}) f_{i}}{1 - λ_{i}} + \\ 900 T [(x_{i} - 1) + \sqrt[]{(x_{i} {- 1)}^{2} + \frac{8 K I_{i} x_{i}}{c_{i} T}}] + \\ 1800 Q_{i} t_{i} (1 + u_{i} \frac{)}{(} c_{i} T) \end{matrix} \end{matrix}$ (4)

式中:I_i= $\begin{matrix} \{\begin{matrix} 1 - 0.91 X_{i}^{2.68}, X_{i} \leq 1 \\ 0.09, X_{i} > 1 \end{matrix} \end{matrix}$

t_i= $\begin{matrix} \{\begin{matrix} 0, Q_{i} = 0 \\ \min \{T, \frac{Q_{i}}{c_{i} [1 - \min (1, x_{i})]}\}, Q_{i} \neq 0 \end{matrix} \end{matrix}$

u_i= $\begin{matrix} \{\begin{matrix} 0, t_{i} < T \\ 1 - \frac{c_{i} T}{Q_{i} [1 - \min (1, x_{i})]}, t_{i} \geq T \end{matrix} \end{matrix}$

P_i为车道组i在绿灯期间到达的车辆所占比例; f_i为车道组i绿灯期间车辆成队列到达的修正系数; K为信号控制类型的延误修正系数; I_i为车道组i的上游调节增量延误修正系数; X_i为车道组i的所有上游有贡献车流按流量进行加权所得的饱和度; Q_i为分析期初车道组i的初始排队车辆数(pcu); t_i为分析期内车道组i不能满足交通需求的时间(h); u_i为车道组i的延误参数.

式(1)~(4)给出的是一条车道或车道组的车均延误, 通过将每条车道或车道组的车均延误进行集计可以得到交叉口的车均延误 $\begin{matrix} \bar{d} \end{matrix}$ , 即:

$\begin{matrix} \bar{d} = \overset{m}{\sum_{i = 1}} d_{i} q_{i} / \overset{m}{\sum_{i = 1}} q_{i} \end{matrix}$ (5)

式中:m为车道组数.

1.5 模型对比

从模型结构来看, Webster延误模型为二项式; HCM1985延误模型为三项式; ARRB延误模型为两段式分段函数, 其中一段为三项式, 另一段为单项式; HCM2000延误模型为三项式, 其中有3个变量为两段式分段函数.为进一步比较这4种车均延误模型在使用过程中的难易程度, 表1归纳了这些模型在计算交叉口车均延误时涉及的直接变量, 间接变量和待定参数的名称和个数.这里直接变量是指那些在使用模型过程中需要通过交通调查获取相应数据的变量; 间接变量是指那些在模型使用过程中根据直接变量进行计算即可获得的变量; 待定参数是指那些在模型使用前需要通过交通调查或参阅相关文献进行确定的变量.从模型结构和变量个数两个角度来看, Webster和HCM1985两种延误模型简单易用; ARRB延误模型较为复杂; HCM2000延误模型最为复杂.此外, 这4种延误模型均适用于单点信号控制交叉口, 其中只有HCM2000延误模型还适用于协调信号控制交叉口^[15].

表1 车均延误模型对比 Table 1 Comparison of the vehicle delay models

2 案例设计

2.1 方案设计

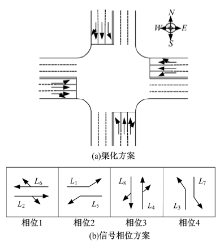
为进一步分析上述车均延误模型的适用性, 设计如图1所示的十字型信号控制交叉口.

图1(a)为该交叉口的渠化方案, 其4条进口道均渠化3条车道, 由内向外分别为左转, 直行和直右车道.图1(b)为该交叉口的信号相位方案, 即东西直行, 东西左转, 南北直行和南北左转4个信号相位, 其中L₁~L₈表示车道组编号.

	Figure Option View Download New Window
	图1 交叉口渠化方案与信号相位方案Fig.1 Channelization scheme and signal phase plan for a four-leg intersection

首先, 通过设置各流向车流的交通量使交叉口饱和度以0.1为增量从0.1变化到1.2, 共12种水平.然后, 信号交叉口采用的周期时长以30 s为增量从60 s变化到180 s, 共5种水平.最后, 使用交叉口饱和度与周期时长进行交叉分类, 形成60组设计方案.表2列出了这60组设计方案的序号, 其序号所在的列和行分别对应其交叉口饱和度与周期时长.所谓交叉口饱和度是指所有车道组的饱和度按流量进行加权所得的饱和度^[16].基于此, 本文不再直接给出机动车交通量数据.

表2 设计方案编号 Table 2 Number of design scenarios

2.2 参数标定

为了设计信号配时方案, 假设每条进口道上的左转, 直行和直右车道的饱和流率分别为1800, 1840和1810 pcu/h; 各进口道交通量相等且均为标准小汽车数, 而且各流向占比相等.

在计算信号配时参数时, 设前损失时间为2 s, 后补偿时间为2 s, 黄灯时间为3 s, 全红时间为0 s, 每相位的绿信比相同.

在计算车均延误时, 对于HCM2000延误模型, 由于交叉口采用单点定时信号控制策略, 那么P_i为λ _i, f_i和I_i为1, K为0.5; 假设初始时刻无滞留排队车辆, 则Q_i为0.

在建立仿真模型时, 为排除折算系数的影响, 车辆类型均选择小汽车; 为拟合饱和流率, 通过改变驾驶行为参数为不同类型的车道设置不同的饱和流率.根据驾驶行为参数和饱和流率的对应关系图, 对于左转, 直行和直右车道, 分别设置安全距离的附加部分为2.50, 2.36和2.43; 安全距离的倍数部分为3.50, 3.36和3.43.此外, 仿真模型中的其他参数采用软件提供的默认值.

为了消除随机因素对仿真结果的影响, 在运行仿真模型时采用多运行模式.鉴于VISSIM用户手册推荐仿真次数为5~20^[14], 为减轻工作量, 本次仿真实验选择仿真5次.另外, 设起始随机种子和随机种子增量均为1, 仿真时间设置为60 min.

3 影响因素分析

3.1 检测区段

在VISSIM中, 延误的检测结果由行程时间检测器提供, 其检测断面的起始, 终止位置以及检测区段长度对延误的测算值有很大影响.

为研究检测区段设置对所得延误的影响, 选取交叉口饱和度与周期时长均不相同的5种设计方案进行交通仿真.首先, 使用仿真软件得到每种方案下各进口道的最大排队长度; 然后, 根据最大排队长度设置10组延误检测区段, 再次运行仿真软件测得延误.

表3给出了起始检测断面的设置对交叉口车均延误的仿真实验值的影响, 进口道最大排队长度中的加粗数字为4个进口道中的最大值, 延误仿真实验值中的加粗数字代表延误趋于稳定的实验值, 偏差在0.2 s以内.

由表3可以看出:① 随着位于停车线上游的起始检测断面距离停车线由近至远, 延误由小变大, 最终趋于稳定; ② 当交叉口饱和度较低, 周期时长较短, 起始检测断面所处位置对延误仿真实验值的影响较小, 反之, 其影响较大; ③ 当起始检测断面与停车线的间距大于最大排队长度的2倍时, 延误测算值趋于稳定.因此, 建议起始检测断面设置在停车线上游, 且与停车线的间距不小于最大排队长度的2倍.另外, 终止检测断面位于停车线下游, 经过仿真实验, 该断面所处位置对延误仿真实验值没有影响.

表3 起始检测断面的设置对交叉口车均延误的仿真实验值的影响 Table 3 Impacts of the settings of the start section on the experimental value of the intersection delay

3.2 分析期

由于不同模型的建模思路和方法不同, 部分延误模型考虑了分析期对延误的影响.一方面, ARRB和HCM2000两种延误模型涉及分析期, 该参数的取值会影响延误的模型计算值.另一方面, 在VISSIM仿真模型中, 分析期是评价车辆延误的一个重要参数, 该参数的取值还会影响延误的仿真实验值.

类似地, 为研究分析期对各模型所得延误的影响, 选取交叉口饱和度与周期时长逐渐增加的5种设计方案, 使用VISSIM仿真模型, ARRB模型和HCM2000模型分别计算这5种设计方案下的交叉口车均延误的仿真实验值或模型计算值.这里分析期选取3个水平, 即15, 30, 60 min.在VISSIM仿真模型中, 起始检测断面距离停车线足够远, 仿真次数为5.

表4显示了分析期对交叉口车均延误的影响.由该表可见, 随着分析期的延长, 3种模型所得延误均呈现递增趋势; 随着交叉口饱和度与周期时长的增加, 采用不同分析期得到的延误的极差不断增大, 即测算的车均延误的差异越来越大.因此, 分析期的取值直接影响延误的测算结果, 这将影响对各车均延误模型适用性的评价.

表4 分析期对交叉口车均延误的影响 Table 4 Impacts of the duration of analysis period on the intersection delay

4 适用性分析

4.1 模型适用性规律

如前所述, 使用不同车均延误模型所测算的延误受分析期, 饱和度, 周期时长等因素的影响.为了分析不同车均延误模型的适用性, 本文将交通仿真软件VISSIM测得的延误称为仿真实验值, 将车均延误模型计算的延误称为模型计算值.根据模型计算值对仿真实验值的吻合程度来评价各延误模型的适用性.为此, 引入车均延误的相对误差, 该参数被定义为:

$\begin{matrix} δ = [({\bar{d}}_{c} - {\bar{d}}_{s}) / {\bar{d}}_{s}] \times 100 % \end{matrix}$ (6)

式中:δ 为车均延误的相对误差(%); $\begin{matrix} {\bar{d}}_{c} \end{matrix}$ 和 $\begin{matrix} {\bar{d}}_{s} \end{matrix}$ 分别为车均延误的模型计算值和仿真实验值(s).

首先, 针对3种分析期, 分别使用Webster模型, ARRB模型, HCM1985模型, HCM2000模型和VISSIM仿真模型计算或检测60组设计方案下的交叉口车均延误.为排除初始排队对延误的影响, 仿真实验值采用每种情况下的第一组数据.其次, 计算4种延误模型与VISSIM仿真模型所得交叉口车均延误的相对误差, 其结果列于表5~表8.

表5显示了Webster模型与VISSIM仿真模型对测算交叉口车均延误的差异.由于Webster模型具有一定局限性, 即当交叉口饱和度接近1.0时, 延误趋于无穷大, 即该模型不适用于交叉口饱和度为1.0, 1.1和1.2的设计方案, 因此这里没有相关数据.从表5可以看出:① 车均延误的相对误差均为负值, 说明Webster模型倾向于低估延误; ② 针对同一种设计方案, 在大多数情况下, 采用15 min分析期所得车均延误的相对误差较小, 这说明Webster模型计算的延误与VISSIM仿真模型最初15 min内测算的延误接近, 换句话说, 在最初15 min内使用Webster模型能够准确地测算延误; ③ 当交叉口饱和度在0.1~0.7时, 车均延误的相对误差能被控制在30%以内, 说明在低饱和度条件下Webster模型能够较好地测算延误.

表5 Webster模型计算值和VISSIM仿真实验值的相对误差 Table 5 Relative errors between the calculated delays from the Webster model and those from the VISSIM model

表6显示了ARRB模型与VISSIM仿真模型对测算交叉口车均延误的差异.由表6可以看出:① ARRB模型有时低估延误, 有时高估延误; ② 当交叉口饱和度在0.1~0.7时, 车均延误的相对误差有正有负, 但能被控制在10%以内, 说明在低饱和度条件下ARRB模型能够较好地测算延误; ③ 当交叉口饱和度在0.8~1.2时, 车均延误的相对误差均为正值, 说明在高饱和度条件下ARRB模型明显高估延误.

表7显示了HCM1985模型与VISSIM仿真模型对测算交叉口车均延误的差异.从表7可以看出:① HCM1985模型有时低估延误, 有时高估延误; ② 当交叉口饱和度小于1.0时, 车均延误的相对误差都为负, 且能被控制在30%以内, 说明在欠饱和条件下HCM1985模型倾向于低估延误; ③ 当交叉口饱和度大于1.0时, 车均延误的相对误差有正有负, 说明在过饱和条件下HCM1985模型对车均延误估计的准确度受分析期, 饱和度与周期时长影响.

表8显示了HCM2000模型与VISSIM仿真模型对测算交叉口车均延误的差异.从表8可以看出:① 车均延误的相对误差只有在极低饱和度条件下可能出现负值, 说明HCM2000模型基本倾向于高估延误; ② 当交叉口饱和度在0.1~0.7时, 车均延误的相对误差能被控制在20%以内, 而当交叉口饱和度小于1.0时, 车均延误的相对误差能被控制在60%以内, 说明在低饱和度条件下HCM2000模型能够较好地测算延误; ③ HCM2000模型对车均延误估计的准确度受分析期, 饱和度与周期时长影响.

表6 ARRB模型计算值和VISSIM仿真实验值的相对误差 Table 6 Relative errors between the calculated delays from the ARRB model and those from the VISSIM model

表7 HCM1985模型计算值和VISSIM仿真实验值的相对误差 Table 7 Relative errors between the calculated delays from the HCM1985 model and those from the VISSIM model

表8 HCM2000模型计算值和VISSIM仿真实验值的相对误差 Table 8 Relative errors between the calculated delays from the HCM2000 model and those from the VISSIM model

4.2 模型适用性对比

为比较4种车均延误模型的适用性, 对表5~表8中交叉口车均延误相对误差的675个数据点进行统计分析.将相对误差绝对值以10%为间隔进行区间划分, 分别统计4个延误模型所得车均延误的相对误差绝对值落在每个区间内的百分比, 如图2所示.

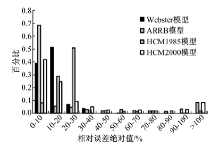	Figure Option View Download New Window
	图2 交叉口车均延误的相对误差绝对值的分布规律Fig.2 Distribution of the absolute values of the relative errors of the intersection delay

从图2可以看出:① Webster模型与VISSIM仿真模型所得车均延误的相对误差绝对值在0~30%范围内的百分比超过95%, 但该模型不适用于高饱和度的情况; ② ARRB模型与VISSIM仿真模型所得车均延误的相对误差绝对值在0~10%范围内的百分比接近70%; ③ HCM1985模型与VISSIM仿真模型所得车均延误的相对误差绝对值在10%~30%范围内的百分比为80%; ④ HCM2000模型与VISSIM仿真模型所得车均延误的相对误差绝对值在0~30%范围内的百分比为75%.比较这些结果可以发现:针对单点信号控制交叉口, 在估计车辆延误方面, ARRB模型的适用性最好, 其次为HCM1985, HCM2000模型, Webster模型的适用性最差.

综上所述, 在4种经典的车均延误模型中, Webster模型存在致命缺陷, HCM2000模型过于复杂但适用范围较广, ARRB模型与HCM1985模型的适用性都较好.与HCM1985模型相比, ARRB模型尽管稍显复杂, 但是与VISSIM仿真模型的差异较小.因此, 当估计单点信号控制交叉口的车辆延误时, 推荐使用ARRB模型.

4.3 模型使用条件

为方便科研人员与工程技术人员在实际应用中选用合适的车均延误模型, 根据各模型的适用性, 表9归纳了4种经典车均延误模型的使用条件.

表9 车均延误模型的使用条件 Table 9 Service conditions of vehicle delay models

5 结束语

为了估计信号交叉口的车辆延误, 通常需要选择合适的车均延误模型.此时, 车均延误模型的适用性是模型选择的一个关键问题.本文基于一定交通需求和信号控制构建了一种实验环境, 从模型结构和变量个数两个角度对比分析了4种经典车均延误模型在模型使用过程中的难易程度.在考虑多种设计方案的基础上, 分析了VISSIM仿真模型中的多个因素对交叉口车均延误测算值的影响.针对每一种设计方案, 使用4种经典车均延误模型计算交叉口车均延误, 并使用VISSIM仿真模型测算交叉口车均延误.以VISSIM仿真模型所测得的车均延误为标准, 对比分析了4种经典车均延误模型的适用性.结果表明, 对于单点信号控制交叉口, Webster模型简单易用, 在高饱和度条件下失效, 其适用性最差, ARRB模型较为复杂, 其适用性最好, HCM1985模型简单易用, 其适用性较好, HCM2000模型最为复杂, 其适用性一般.这些研究成果可以为正确选择与应用车均延误模型提供依据.

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Webster F V. Traffic signal settings[R]. Road Research Technical Paper No. 39, London: Road Research Laboratory, Her Majesty Stationary Office, 1958. [本文引用:2]
[2]	Akçelik R. Traffic signals: capacity and timing analysis[R]. Research Report No. 123, Vermont South: Australian Road Research Board, 1981. [本文引用:2]
[3]	Transportation Research Board (TRB). Highway capacity manual 1985[R]. Washington DC: National Research Council, 1985. [本文引用:2]
[4]	Transportation Research Board (TRB). Highway capacity manual 2000[R] . Washington DC: National Research Council, 2001. [本文引用:2]
[5]	Arasan V T, Jagadeesh K. Effect of heterogeneity of traffic on delay at signalized intersections[J]. Journal of Transportation Engineering, 1995, 121(5): 397-404. [本文引用:1]
[6]	沈旅欧, 刘好德. 信号交叉口控制延误算法的适应性研究[J]. 同济大学学报: 自然科学版, 2012, 40(4): 559-563. Shen Lyu-ou, Liu Hao-de. Applicability study of different control delay calculation methods[J]. Journal of Tongji University (Natural Science), 2012, 40(4): 559-563. [本文引用:1]
[7]	Lin F B, Mazdeyasna F. Delay models of traffic-actuated signal controls[J]. Transportation Research Record, 1983, 905: 33-38. [本文引用:1]
[8]	van Zuylen H J, Viti F. Delay at controlled inter-sections: the old theory revised[C]//2006 IEEE Intelligent Transportation Systems Conference, Toronto, Canada, 2006: 17-20. [本文引用:1]
[9]	庄焰, 曾文佳. 信号交叉口延误计算模型研究[J]. 深圳大学学报: 理工版, 2006, 23(4): 309-313. Zhuang Yan, Zeng Wen-jia. Study of traffic delay model at signalized intersection[J]. Journal of Shenzhen University (Science and Engineering), 2006, 23(4): 309-313. [本文引用:1]
[10]	Akgüngör A P. A new delay parameter dependent on variable analysis periods at signalized intersections. part 1: model development[J]. Transport, 2008, 23(1): 31-36. [本文引用:1]
[11]	Mazloumi E, Moridpour S, Mohsenian H. Delay function for signalized intersections in traffic assignment models[J]. Journal of Urban Planning and Development, 2010, 136(1): 67-74. [本文引用:1]
[12]	Chen P, Liu H, Qi H S, et al. Analysis of delay variability at isolated signalized intersections[J]. Journal of Zhejiang University (Science A), 2013, 14(10): 691-704. [本文引用:1]
[13]	Dion F, Rakha H, Kang Y S. Comparison of delay estimates at under-saturated and over-saturated pre-timed signalized intersections[J]. Transportation Research Part B, 2004, 38(2): 99-122. [本文引用:1]
[14]	VISSIM 5. 30-05 User Manual[M]. Germany : Planung Transport Verkehr (PTV) AG, 2011. [本文引用:2]
[15]	姚荣涵, 彭程, 周红媚. 协调控制交叉口短车道长度和配时参数协同优化[J]. 吉林大学学报: 工学版, 2015, 45(4): 1082-1087. Yao Rong-han, Peng Cheng, Zhou Hong-mei. Synergistic optimization of short lane length and signal timing parameters for adjacent intersections with coordinated signals[J]. Journal of Jilin University(Engineering and Technology Editon), 2015, 45(4): 1082-1087. [本文引用:1]
[16]	Roess R P, Prassas E S, McShane W R. Traffic Engineering[M]. 3rd ed. Beijing: China Machine Press, 2008. [本文引用:1]

1958

0.0

... 目前,受到业界广泛认同的车均延误模型包括Webster模型^[1],ARRB模型^[2],HCM1985模型^[3]和HCM2000模型^[4] ...

... 1 Webster延误模型1958年,Webster^[1]在假设车辆到达服从泊松分布的基础上,通过修正给出的车均延误模型为: ...

1981

0.0

... 目前,受到业界广泛认同的车均延误模型包括Webster模型^[1],ARRB模型^[2],HCM1985模型^[3]和HCM2000模型^[4] ...

... elik^[2]基于稳态理论提出车均延误模型,该模型也被称为ARRB模型: ...

1985

0.0

... 目前,受到业界广泛认同的车均延误模型包括Webster模型^[1],ARRB模型^[2],HCM1985模型^[3]和HCM2000模型^[4] ...

... 3 HCM1985延误模型1985年,美国通行能力手册(HCM)在假设车辆随机到达的基础上,利用协调变换方法得到的车均延误模型^[3]为: ...

2001

0.0

... 目前,受到业界广泛认同的车均延误模型包括Webster模型^[1],ARRB模型^[2],HCM1985模型^[3]和HCM2000模型^[4] ...

... 4 HCM2000延误模型2000年,美国通行能力手册(HCM)将车均延误模型修正为^[4]: ...

1995

0.0

... 针对不均衡交通情况,Arasan等^[5]通过考虑不同车辆组之间的交互作用采用一次二阶矩概率方法估计了信号交叉口的车辆延误 ...

2012

0.0

. 2012, 40(4):559-563 DOI:doi:10.3969/j.issn.0253-374x.2012.04.010

Applicability study of different control delay calculation methods

信号交叉口控制延误算法的适应性研究

Shen Lyu-ou , Liu Hao-de.

沈旅欧, 刘好德

针对美国HCM 2000基于车道组计算信号交叉口控制延误方法中对同一车道组内各车道使用不均衡情况的处理方式与实际情况不符合的问题，依托交叉路口实例分析了基于车道组和基于车道两种控制延误计算方法的差异，且对Webster延误计算公式以及排队论模型进行了探讨，分析了造成此差异的原因，得出了基于车道组和基于车道的两种控制延误计算方法的适用条件，并对普遍采用的控制延误计算方法及计算工具的开发提出了改进建议.研究成果对于准确计算信号交叉口控制延误、指导相应的辅助计算工具开发具有参考价值.

... 沈旅欧等^[6]通过实例分析了基于车道组和基于车道的两种控制延误计算方法的适用条件 ...

1983

0.0

... 针对利用请求检测器和连续相位的半感应和全感应控制,Lin等^[7]基于修正的韦伯斯特模型提出了用于评价替代配时方案的延误模型 ...

2006

0.0

... 为了清楚地理解溢出排队,van Zuylen等^[8]运用描述排队长度概率分布的马尔科夫链模型分析了交叉口的延误计算问题,进而针对定时交通控制导出了新的延误公式 ...

2006

0.0

. 2006, 23(4):309-313 DOI:doi:10.3969/j.issn.1000-2618.2006.04.005

Study of traffic delay model at signalized intersection

信号交叉口延误计算模型研究

Zhuang Yan, Zeng Wen-jia

庄焰, 曾文佳

摘　要：利用深圳市主要信号交叉口延误实际调查结果,结合美国2000年版HCM延误模型计算结果,应用最小二乘法对模型进行修正,建立与深圳市交叉口延误相符合的延误计算模型,为深圳市信号交叉口和道路系统的分析评价提供了理论依据.

... 为使延误模型能准确地估计特定场景下的车辆延误,庄焰等^[9]利用中国的实际调查数据采用最小二乘法修正了HCM2000延误模型 ...

2008

0.0

... r^[10]通过将延误参数作为分析期的函数而非固定值提出了一种新的信号交叉口延误模型,并与现有的4种延误模型进行了性能对比 ...

2010

0.0

... Mazloumi等^[11]通过考虑驾驶员行为提出了一种适用于交通分配模型的延误函数 ...

2013

0.0

... 针对孤立,定时控制交叉口,Chen等^[12]提出了一种延误可变性分析模型,研究了饱和度和到达规律对延误可变性的影响 ...

2004

0.0

... 针对欠饱和与过饱和情况,Dion等^[13]比较了确定性排队模型,冲击波模型,韦伯斯特稳态模型以及1981年澳大利亚通行能力指南,1995年加拿大通行能力指南,1994和1997版通行能力手册定义的排队模型与INTEGRATION微观交通仿真软件对延误估计的结果 ...

2011

0.0

... 此外,微观交通仿真软件VISSIM以单个车辆为研究对象,通过模拟车辆的运行轨迹可以准确地获取每条车道或车道组上单个车辆的延误数据,并进而集计成进口道或交叉口的延误数据^[14] ...

... 鉴于VISSIM用户手册推荐仿真次数为5~20^[14],为减轻工作量,本次仿真实验选择仿真5次 ...

2015

0.0

. 2015, 45(4):1082-1087 DOI:doi:10.13229/j.cnki.jdxbgxb201504009

Synergistic optimization of short lane length and signal timing parameters for adjacent intersections with coordinated signals

协调控制交叉口短车道长度和配时参数协同优化

Yao Rong-han , Peng Cheng , Zhou Hong-mei.

姚荣涵, 彭程, 周红媚

To optimally allocate the time and space resources for two adjacent intersections with coordinated signals and short left-turn lanes on the common section of a road, an optimization model was presented to jointly obtain the signal cycle length and green slit for each intersection. The objectives are to maximize the passing capacity of the entire intersection and minimize the total delay of vehicles. The decision variables of the model are the length of each short left-turn lane and the effective green time per phase. A case was designed to verify the effectiveness of the proposed model. First, two signal timing plans for each intersection were obtained using the proposed model and Webster model, respectively. Then, the offset between coordinated phases was calculated by a known method. Finally, the traffic operations under the two signal timing scenarios were simulated using VISSIM software. The outcomes show that the unit delay is decreased by 30% and the vehicle throughput is slightly increased for each intersection under the optimization scenario.

为了优化配置共有路段上均含左转短车道的相邻协调控制交叉口的时空资源,以最大化交叉口通行能力和最小化车辆总延误为目标,以左转短车道长度和相位有效绿灯时间为决策变量,建立了交叉口周期时长与绿信比组合优化模型。为验证优化模型的有效性,设计了一个案例,使用优化模型和韦伯斯特模型分别获得每个交叉口的配时方案,并使用已有方法计算了相邻交叉口协调相位的绿时差,进而使用VISSIM软件模拟了两种配时方案下的交通流运行状况。结果显示:与韦伯斯特方法相比,本文优化方法能使交叉口车均延误降低约30%,而通过车辆数略有增加。

... 此外,这4种延误模型均适用于单点信号控制交叉口,其中只有HCM2000延误模型还适用于协调信号控制交叉口^[15] ...

2008

0.0

... 所谓交叉口饱和度是指所有车道组的饱和度按流量进行加权所得的饱和度^[16] ...