作者简介:季彦婕(1980-),女,副教授,博士.研究方向:交通诱导信息系统.E-mail:jiyanjie@seu.edu.cn
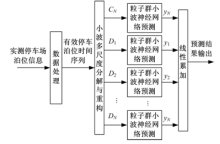
基于停车场有效停车泊位短时变化特性,提出了一种小波变换和粒子群小波神经网络组合预测方法.首先,通过选择合适的小波函数对有效停车泊位时间序列进行多尺度的小波分解与重构,然后对重构后的时间序列分别采用小波神经网络进行预测,并利用粒子群算法对神经网络初始参数的选取进行优化,最后将各自外推的预测结果进行合成,得到最终预测结果.实例分析表明:与单独使用小波神经网络模型相比,小波变换-粒子群小波神经网络模型的预测精度提高了5~7倍,且预测稳定性较好.
A forecasting model was proposed based on the short-term changing characteristics of Available Parking Space (APS). This model integrates the wavelet analysis, Particle Swarm Optimization (PSO) and Wavelet Neural Network (WNN). First, the APS time series were decomposed and reconstituted by wavelet analysis. Then, WNN model was used to forecast the reconstructed time series respectively. The PSO method was employed to optimize the selection of the initial parameters of the neural network. Finally, the final forecasted ASP was induced by integrating the prediction results. A case study was carried out to verify the applicability of the proposed model. Compared with simple WNN model, the new method enjoys higher accuracy and stable performance that the APS forecasting can be improved by 5 to 7 times by this new method.
停车场是否有空余泊位可供停车是驾车者停车选择时最为关注的问题之一.利用停车泊位信息采集技术获得停车场内空余车位信息并对其进行实时预测是停车诱导信息系统的一项关键技术.实时, 准确地预测出停车场的空余车位信息, 供系统用户选择停车场时参考, 不仅有利于用户合理地安排自己的出行, 也有利于交通管理部门对交通的宏观调控.纳入停车诱导信息系统的停车泊位主要是指公共停车设施内可供社会车辆停放的车位, 被单位或个人长期租用的固定车位不在研究范围之内.因此, 本文采用有效停车泊位来直观地描述停车场可供利用的泊位情况.有效停车泊位是指正在开放的停车场内未被车辆或其他物品占用, 可以用来停放车辆的停车泊位[1].
停车场的泊位变化受诸多因素的影响, 如停车场类型, 所处位置, 天气, 事件等, 多因素的作用造成了泊位变化的复杂性和随机性.近年来, 国内外学者建立了多种泊位短时预测模型, 如模糊神经网络, 一般BP网络方法[1], 基于相空间重构和Elman神经网络相结合方法[2], 自回归移动平均模型[3], 基于混沌时间序列的加权一阶局域预测方法[4], 马尔可夫模型[5, 6, 7].在这些预测方法中, 神经网络模型有较强的容错性和鲁棒性, 具有识别非线性复杂系统的特点, 较适合于有效停车泊位短时预测, 但神经网络具有易陷入局部极小和引起振荡效应现象的缺点, 预测效果会有较大的随机波动.考虑到小波分析在非平稳时间序列的预测中有较好的应用[8], 粒子群算法具有很强的全局搜索能力, 应用于神经网络初始参数的选取可以有效避免神经网络陷入局部最优, 本文拟根据有效停车泊位的短时变化特性, 提出小波变换-粒子群小波神经网络组合预测模型, 并通过实例分析验证本文所提出的预测模型的有效性.
以英国纽卡斯尔市埃尔登停车楼2011年9月12日(星期一)至9月16日(星期五)的统计数据为例, 分析该停车场有效停车泊位的短时变化特性(见图1).总体而言, 各天的有效停车泊位变化趋势大致相同, 但时间间隔越短, 各种随机干扰造成的影响就越大, 有效停车泊位的变化越剧烈.
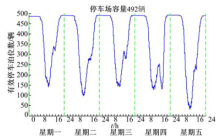 | 图1 埃尔登停车楼9月12日至9月16日全天有效停车泊位变化曲线Fig.1 Whole day's available parking space change curve in Eldon Multi parking lot (from 12-9-2011 to 16-9-2011) |
为了能细致地刻画有效停车泊位时间序列微观动力学特征, 本文采用波动率来直接反映有效停车泊位相邻数据间的波动特征[9]:设时间序列为s(k), 则s(k)的波动率为v(m)=[s(m+1)-s(m)]/s(m), m=1, 2, , et al., n-1; 其中k=1, 2, , et al., n为对应的序号, 并根据有效停车泊位时间序列的波动率值绘制得到相应的波动率图, 如图2所示.
由图2可以看出:在每天12:00~16:00时间段内, 有效停车泊位时间序列波动率较大且表现不规则, 其余部分时间段的波动率虽相对较小, 但波动的规律性也较弱, 传统的短时预测方法无法做到准确预测.而小波分析正是处理这些非平稳数值信号的有力工具, 在非平稳时间序列的分析和预测中都有较好的应用.本文尝试通过小波变换将时间序列中的干扰信号屏蔽在高频信号中, 并结合粒子群算法对小波神经网络的参数进行优化选取, 提出小波变换-粒子群小波神经网络组合预测模型.
如图3所示, 小波变换-粒子群小波神经网络模型的具体预测流程如下:
(1)选用某一小波函数对有效停车泊位时间序列进行多分辨率的N尺度的分解, 分解后得到一个尺度为N的低频系数向量cN 和N个不同尺度下的高频系数向量d1, d2, , et al., dN .
(2)用指定的小波函数分别对信号的低频部分cN 和高频部分d1, d2, , et al., dN 进行多尺度重构, 得到N+1个时间序列CN, D1, D2, , et al., DN .其中, CN 为低频信号, 反映有效停车泊位本质变化趋势; D1, D2, , et al., DN为高频干扰信号, 反映有效泊位的随机变化趋势.
(3)对
(4)使用粒子群小波神经网络模型进行预测, 得到N+1个预测结果
(5)将上述N+1个预测结果累加, 获得对应于原始有效停车泊位的预测结果, 即
由于有效停车泊位预测中用的是离散的时间序列, 故引入离散小波变换(DWT)中的二进正交小波变换, 并采用快速二进正交小波变换算法(简称Mallat算法)进行小波分解和重构.
Mallat算法[10]表示为:
式中:H和G分别为低通滤波器和高通滤波器; c0 为原始时间序列, 可以将原始时间序列分解为高频系数向量d1, d2, , et al., dN 和低频系数向量cN .
经Mallat算法分解后的序列可以用重构算法进行重构:
2.3.1 小波神经网络
本文中的小波神经网络以三层BP神经网络的拓扑结构为基础, 是一种以小波基函数作为隐含层节点的传递函数, 信号向前传播而误差向后传播的神经网络[11], 其拓扑结构如图4所示.网络输入节点数为r, 隐层节点数为l, 输出节点数为m.本文中输出节点只有一个, 即m为1.
设小波神经网络的输入信号可以表示为一个一维向量xi (i=1, 2, , et al., r), 输出信号表示为y(k)(k=1, 2, , et al., m).隐含层输出的计算公式为:
式中:h(j)为隐含层第j个节点的输出值; ω ij 为输入层i节点和隐含层j节点间的连接权值; φ (x)为小波基函数; bj 为小波基函数的平移因子; aj为小波基函数的伸缩因子.
本文中的小波基函数选用母小波基函数:
小波神经网络输出层预测值的计算公式为:
式中: ω jk 为隐含层j节点和输出层k节点间的连接权值.
本文中的小波神经网络的权值和阈值的修正算法采用梯度修正法来更新网络权值和小波基函数参数, 从而使小波神经网络预测输出不断逼近期望输出.
2.3.2 粒子群算法
粒子群算法(PSO)是一种基于群体智能理论的优化算法.粒子群的个体(这里称作粒子)代表问题的一个可能解.每个粒子具有位置和速度两个特征.粒子位置坐标对应的目标函数值即可作为该粒子的适应度.算法通过适应度来衡量粒子的优劣.首先初始化一群随机粒子, 然后通过迭代找到最优解.在每一次迭代中, 粒子通过跟踪两个"极值"来更新自己:一个是粒子本身所找到的最优解, 即个体极值pBest; 另一个是整个粒子群目前找到的最优解, 称之为全局极值gBest.
粒子在找到上述两个极值后, 就根据下面两个公式来更新自己的速度与位置[12]:
式中:
在迭代过程中, 粒子每一维的更新速度都被限制在最小和最大更新速度[-Vmax, Vmax]之间, 粒子每一维的坐标也被限制在合理范围内.同时, 每个粒子的个体极值pBest和整个粒子群的全局极值gBest在不断地更新, 最终得到的gBest就是算法得到的最优解.
2.3.3 粒子群小波神经网络预测流程
利用上文介绍的粒子群算法对小波神经网络的初始权值和阈值进行最优选取.
粒子群算法的适应度函数选为小波神经网络的训练误差均方差, 即:
式中:N为训练样本数; yn(k)为第k个点的期望输出; y(k)为第k个点的实际输出值.
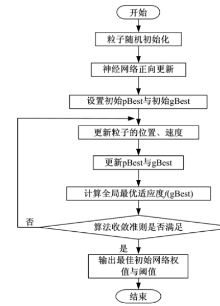
混合模型通过粒子群算法的优化搜索来训练网络参数, 以获得尽可能低的训练误差, 其具体的训练流程图如图5所示.
训练完成后将输出的网络权值和阈值作为小波神经网络的初始权值和阈值, 对有效停车泊位数进行预测.
本文试验数据来源于英国纽卡斯尔市埃尔登停车楼2011年9月12日至9月16日和纽卡斯尔市约翰停车楼2011年11月8日至11月11日全天的停车泊位信息, 并将其处理成以1 min为间隔的有效停车泊位时间序列.
由于两处停车楼工作日夜间22:00到凌晨6:00几乎没有车辆停泊, 停车需求较低, 因此本文均以两个停车楼前三天6:00~22:00时间段内的2883个数据作为训练样本, 剩余一天6:00~22:00时间段内的961个数据作为测试样本, 分别对两个停车楼有效停车泊位进行预测.
误差指标采用测试样本的均方差:
本文选用"db2"函数作为小波分析函数, 利用后验的方法对原始有效停车泊位时间序列采取5层分解, 得到6个子有效停车泊位时间序列:高频干扰时间序列D1~D5以及低频确定时间序列C5.
粒子群的种群规模设置为30, 进化代数设置为200, 神经网络正向更新时迭代次数为10, 最优适应度
结合粒子群算法的小波神经网络为三层拓扑结构, 输入层数目设为3, 即输入当前时间点的前3个时间间隔的有效停车泊位数, 隐含层数目经多次对比试验设为6, 输出层为1, 即输出下一个时间间隔的有效停车泊位数.初始网络权值和阈值为粒子群算法输出结果.设置网络学习速率为0.01, 收敛误差与粒子群最优适应度相同.为了在相同的训练次数下比较小波神经网络模型与粒子群小波神经网络模型的预测精度, 单独使用小波神经网络模型预测时的迭代学习次数为:种群规模× 进化次数× 神经网络正向更新时的迭代次数=30× 200× 10=60000次.
根据以上所述的参数设置, 将通过粒子群算法训练好的初始权值和阈值代入小波神经网络中训练.为减少训练时间, 在利用小波神经网络预测时, 高频干扰时间序列(D1~D5)均采用从低频确定时间序列(C5)中训练得到的初始权值与阈值.
由于各模型预测效果具有随机性, 故本文对于埃尔登停车楼与约翰停车楼的有效泊位数据分别利用前文所述的3种预测模型进行了5次预测试验, 在一定程度上降低了偶然性的影响.表1中记录了对于小波神经网络(WNN), 粒子群小波神经网络(PSO-WNN)和基于小波变换的粒子群小波神经网络(WA-PSO-WMM)5次试验的预测均方差(MSE).5次预测的均方差(MSE)平均值和标准差记录在表2中, 计算如下:
| 表1 各模型5次试验的预测均方差 Table 1 Prediction MSE of three models in five experiments |
| 表2 各模型5次预测的MSE平均值和标准差以及训练时间 Table 2 Average MSE, standard deviation, and training time of three models in five experiments |
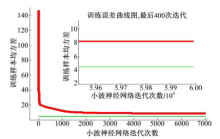
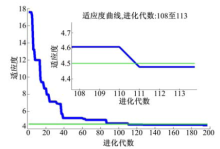
以埃尔登停车楼为例, 图6和图7分别表示了在埃尔登停车楼试验数据的训练过程中, 小波神经网络随迭代次数的增加其训练误差的变化以及粒子群算法中适应度(本文中即训练误差)随进化代数的变化.可以看出:单纯使用小波神经网络进行迭代训练时, 当迭代次数大于5000次, 训练误差几乎不再减少, 算法陷入局部最优, 60 000次迭代结束后离收敛误差还有一定差距.而利用粒子群算法的全局搜索能力有利于神经网络达到收敛误差, 一定程度上避免了网络训练陷入局部最优.试验表明:实际上单独应用小波神经网络进行预测时, 最大迭代次数设置为5000次即可, 此时网络训练时间约为8 min.
各个模型第5次试验12:30~14:30间的拟合曲线图如图8, 图9所示.
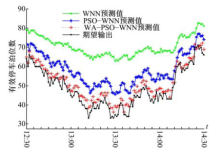 | 图8 各模型第5次试验的拟合曲线图(埃尔登停车楼)Fig.8 Fitting curve of fifth experiment of three forecasting models(Eldon Multi parking lot) |
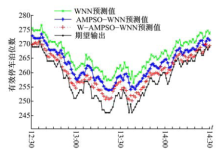 | 图9 各模型第5次试验的拟合曲线图(约翰停车楼)Fig.9 Fitting curve of fifth experiment of three forecasting models(John Dobson parking lot) |
从图表中可以看出:
(1)在埃尔登停车楼和约翰停车楼的有效停车泊位预测试验中, 与随机选取初始权值和阈值的WNN模型相比, PSO-WNN模型的预测精度均有所提高, 而WA-PSO-WNN模型的预测精度则提高了5~7倍, 应用于有效停车泊位短时预测有较好的预测效果.
(2)与WNN模型相比, PSO-WNN模型和WA-PSO-WNN模型预测误差的标准差较小, 即使用粒子群优化算法可以使得模型的预测精度波动较平缓, 稳定性较好, 增强了停车泊位预测的可靠性.
(3)粒子群算法所需要的训练时间较长, 可以利用停车场停车需求不高的时间段对模型进行训练, 如埃尔登停车楼夜间22:00至凌晨6:00.
在分析有效停车泊位短时变化特性的基础上, 提出了一种小波变换和粒子群小波神经网络组合预测模型, 用于有效停车泊位的短时预测.通过小波变换将时间序列中的干扰信号屏蔽在高频信号中, 对重构后的时间序列采用小波神经网络进行预测, 并结合粒子群算法对小波神经网络的参数进行优化选取.以英国纽卡斯尔市埃尔登停车楼和约翰停车楼为例, 利用所提出的组合预测模型对有效停车泊位进行短时预测.实例分析表明:与单独使用小波神经网络相比, 组合预测模型的预测精度提高了5~7倍; 通过粒子群算法对小波神经网络进行参数优化, 可以提高组合预测模型的预测稳定性; 考虑到粒子群算法所需训练时间较长, 可以利用停车需求较低的时间段对模型进行训练.
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|