引用本文
宗芳, 王占中, 贾洪飞, 焦玉玲, 吴杨. 基于支持向量机的通勤日活动-出行持续时间预测.吉林大学学报:工学版, 2016, 46(2): 406-411
ZONG Fang, WANG Zhan-zhong, JIA Hong-fei, JIAO Yu-ling, WU Yang. Prediction of commuter's daily activity-travel duration time with support vector regression. Journal of Jilin University Engineering and Technology Edition, 2016, 46(2): 406-411  
Permissions
Copyright©2016, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
基于支持向量机的通勤日活动-出行持续时间预测
宗芳, 王占中, 贾洪飞, 焦玉玲, 吴杨
吉林大学 交通学院,长春 130022
通讯作者:王占中(1965-),男,教授,博士.研究方向:运输系统规划,生产物流运作与优化技术.E-mail:wangzz@jlu.edu.cn

作者简介:宗芳(1979-),女,副教授,博士.研究方向:交通行为分析.E-mail:zongfang@jlu.edu.cn

基金:国家自然科学基金项目(50908099, 51278221); 教育部人文社科青年基金项目(14YJC630225); 吉林大学国家优秀青年科学基金后备人选培育计划项目
摘要

构建了通勤者的日活动-出行链,并给出其时间构成要素,对比分析了Hazard和回归支持向量机模型的预测精度,应用回归支持向量机模型建立了出行耗时预测模型和活动持续时间预测模型,预测了通勤日活动-出行链中各次出行的出行耗时和各次活动的持续时间,并应用已建模型考察公交优先策略对出行耗时的影响.研究表明:本文所建模型能够以较高精度预测通勤者的日出行耗时和活动持续时间,在出行耗时预测中回归支持向量机的预测精度高于Hazard模型,相关影响因素分析也有助于掌握居民的通勤出行时间决策规律.研究成果可以为构建通勤日活动-出行行为预测模型系统提供连续时间预测模块,也可以为交通需求管理政策的制定和实施提供决策依据.

关键词: 交通运输工程; 通勤出行时间; 回归支持向量机
中图分类号:U491.1 文献标志码:A 文章编号:1671-5497(2016)02-0406-06
Prediction of commuter's daily activity-travel duration time with support vector regression
ZONG Fang, WANG Zhan-zhong, JIA Hong-fei, JIAO Yu-ling, WU Yang
College of Transportation, Jilin University, Changchun 130022, China
Abstract

The commuter's daily activity-travel schedule is proposed and its key time allocation is investigated. According to the comparison of hazard model and Support Vector Regression (SVR) model, travel time prediction models and activity duration prediction models are developed by employing SVR. Then, the continuous time allocation, i.e. all the travel times and activity durations in daily activity-travel schedule are derived and the transit priority policy is evaluated using these models. The results indicate that the model system has a high level of prediction accuracy, and the goodness-of-fit of SVR models is higher than that of Hazard models. This study provides useful insights into commuter's activity-travel time allocation decision. It also serves a foundation that future models of full-scale daily activity-travel pattern can be built on. Moreover, it provides potential for transportation demand management policy analysis.

Keyword: engineering of communications and transportation; commute travel time; support vector regression
0 引 言

日活动-出行链的时间构成要素包括活动时间和出行时间, 以往研究多将二者分开考虑.例如, 在出行时间预测方面, 隽志才等[1]应用Hazard模型预测日出行链中的出行耗时; Bhat[2]和Small[3]分别构建Ordered generalized extreme value(OGEV)模型和非集计经济模型, 预测了购物出行和早通勤的出发时段.在活动时间预测方面, Bhat等[4, 5]应用Hazard模型预测购物活动耗时, 并结合应用连续-离散方法预测活动开始时间和活动持续时间.另外, 以上这些研究多数均仅考虑日活动链中的一部分[2, 3, 4, 5].也有学者[6]结合出行时间预测和活动时间预测, 整体预测通勤日活动-出行时间, 但仅考虑了典型的通勤日活动-出行链, 即仅包含早晚通勤出行, 不包含早晚出行和工作子往返行程.本文将构建完整的通勤日活动-出行链, 对全日所有出行和活动的持续时间进行整体建模预测.

1 日通勤活动链和时间要素

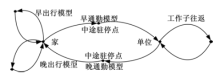
一般来说, 日通勤活动链由图1所示的5个部分组成:① 早出行:指早通勤离家之前的出行和活动, 例如晨练; ② 早通勤:由家到工作单位的出行; ③ 工作子往返:基于工作单位的子往返行程, 如中午从单位出门吃饭; ④ 晚通勤:由工作单位回家的出行; ⑤ 晚出行:下班回家后的出行和活动.每部分又可能由一次以上的出行或者中途驻停组成.为了减少模型复杂度, 仅考虑每部分的第一次出行以及早通勤或晚通勤中的第一次中途驻停.

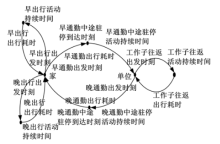
图1 日通勤活动-出行链Fig.1 Daily commute activity-travel pattern

将所有通勤出行时间要素分为离散时刻和连续时间两类.其中离散时刻包括出发时刻和中途驻停到达时刻, 连续时间包括出行耗时和活动持续时间, 从而确定通勤日活动链中的时间要素(见图2).本文仅预测连续时间, 通勤日活动链中的连续时间要素包括:① 出行耗时:早出行耗时, 早通勤出行耗时, 工作子往返出行耗时, 晚通勤出行耗时和晚出行耗时; ② 活动持续时间:早出行活动持续时间, 早出行中途驻停时间, 工作子往返活动持续时间, 晚通勤中途驻停持续时间和晚出行活动持续时间.

图2 通勤日活动-出行时间要素Fig.2 Key time and duration values in daily commute activity-travel pattern

2 模型建立
2.1 数据和变量

本文数据取自2006年北京市居民日出行调查.调查区域为该市18个区, 涉及人口13.8万(约为常驻总人口的1.17%).经数据筛选得到包括54 398个家庭138 480名居民的202 883次出行数据以及出行者个人和家庭属性数据, 主要数据项及统计结果见表1.其中, 出行目的中的工作包括上班, 上学, 回家, 工作外出等; 生活包括购物, 看病, 探亲访友等; 娱乐包括休闲健身, 文化娱乐等; 其他包括乘车, 换乘, 回程等.

表1 模型变量及数据统计 Table 1 Variables and statistics based on survey data

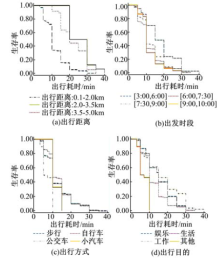
以早出行耗时为例, 应用Stata软件绘制在几个主要因素影响下早出行耗时的分布曲线, 如图3所示.图中横坐标表示出行耗时, 纵坐标表示出行耗时能维持到某一时间点的概率.由图3(a)可见, 随着出行距离的逐渐增大, 出行耗时逐渐增加.结果表明, 另外3个变量, 即出发时段, 出行方式和出行目的也均对早出行耗时有显著影响.

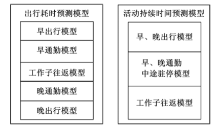
图3 主要因素对早出行耗时的影响Fig.3 Influences of key factors on before-work travel time

2.2 模型框架及建模方法

建立出行耗时预测和活动持续时间预测两组模型, 模型框架见图4.

图4 连续时间预测模型框架Fig.4 Modeling framework of continuous times in commuter's daily schedule

Hazard模型是近年来进行连续时间预测所采用的主要模型[1, 4, 6].然而, 一些学者的研究表明[7], 回归支持向量机(Support vector regression, SVR)在连续时间预测方面具有较高的正确性和可靠性, 应用SVR方法进行出行时间预测可以大大减少相对均值误差和均方根误差.因此, 本文将验证Hazard模型和SVR模型在持续时间预测中的精确度, 选择精度高的模型建立持续时间预测模型.

2.2.1 回归支持向量机

支持向量机(Support vector machines, SVM)是近年来出现的一种新的数据分析和模式识别的机器学习方法.主要研究如何从有限观测数据中挖掘出目前尚不能通过原理分析得到的规律, 并利用这些规律对未知数据或无法观测的新现象进行预测和判断[8].SVR是SVM的一种, 用于连续独立变量的回归建模.

已知 l组关系未知的数据样本 (x1y1), (x2y2), …, (xiyi), …, (xlyl), 其中xi∈X⊆Rm, yi∈Y⊆Rn, l为训练样本的数量, SVM可以利用一个非线性映射 φ将数据 x映射到非线性高维特征空间, 并在这个高维特征空间进行线性逼近, 从而找到映射函数, 使其能更好地逼近已知的数据样本.SVM的基本形式为:

f(x)=w·φ(x)+bw, x∈Rm, b∈Rn(1)

式中:φ(x)为从输入空间x到非线性高维特征空间的映射;w为参数;b为阈值.

将回归估计问题定义为对一个损失函数进行风险最小化的问题, 而最优的回归函数是通过在一定的约束条件下进行最小化, 规则化风险泛函见式(2).

12‖w‖2+C1l∑i=1lLeyi, fxi(2)

式中:第一项使函数更为平坦, 以提高泛化能力, 称为规则化项; 第二项为经验风险泛函, 由不同的损失函数确定; 常数 C> 0, 控制对超出误差 ε的样本的惩罚程度, 用于在结构风险和经验风险之间进行平衡, 采用 ε不敏感损失函数:

Leyi, fxi=maxyi-fxi-ε, 0(3)

对于 Leyi, fxi, 如果估计输出 fxi与期望输出 yi的偏差的绝对值小于 ε, 则 Leyi, fxi等于0; 否则, Leyi, fxi等于偏差的绝对值减去 ε, 通过引入非负的松弛变量 ξi、ξi* , 式(2)可重新描述为:

min12‖w‖2+C1l∑i=1lξi+ξi* (4)

s.t.yi-w·φ(xi)-b≤ε+ξiw·φ(xi)+b-yi≤ε+ξi* ξi* ≥0, i=1, …, l(5)

式(5)为凸二次优化问题, 引入拉格朗日函数, 可得:

w-∑i=1laixi-ai* xi=0(6)

式中: ai、ai* 为拉格朗日乘数, 因此有:

fx=∑i=1lai-ai* φxi·φxj+b(7)

将核函数 Kxixj代入式(7)可得:

fx=∑i=1lai-ai* Kxixj+b(8)

式中: Kxixj为 xi和 xj在特征空间 φxi和 φxj上的内积, 即 Kxixj=φxi·φxj.通过核函数, 所有运算都不必映射到高维特征空间, 可以直接在输入空间中计算, 本文选用径向基核函数[9].

2.2.2 Hazard模型

将非负持续时间T(连续的出行耗时或活动持续时间)看作随机变量, 将T的条件概率定义为风险函数h(t), 表示一次出行或活动在持续时间t之后的某一时点结束的瞬时概率, 即:

h(t)=limΔ→0+P(t≤T< (t+Δ)T> t)Δ(9)

式中: Δ为无穷小区间.

T的概率密度函数和概率分布函数分别为f(t)和F(t):

f(t)=limΔ→0+P(t≤T< (t+Δ))ΔF(t)=P(T≤t)=∫0tf(u)du(10)

定义生存函数S(t)为出行耗时或活动持续时间大于t的概率, 则h(t)与f(t)、F(t)和S(t)之间的关系为:

h(t)=f(t)S(t)=dF(t)/dtS(t)=-dS(t)/dtS(t)=-dlnS(t)dt(11)

假设风险函数服从指数分布, 建立出行耗时或活动持续时间的加速失效时间模型, 风险函数h(t)及生存函数s(t)分别为:

ht=expβ0+β1x1+β2x2+…+βixi(12)

st=exp-expβ0+β1x1+β2x2+…+βixi(13)

式中: x1, …, xi为影响出行耗时或活动持续时间的因素; β0为常数项, β1, …, βi为各影响因素的权重系数.

2.3 SVR与Hazard的精度对比

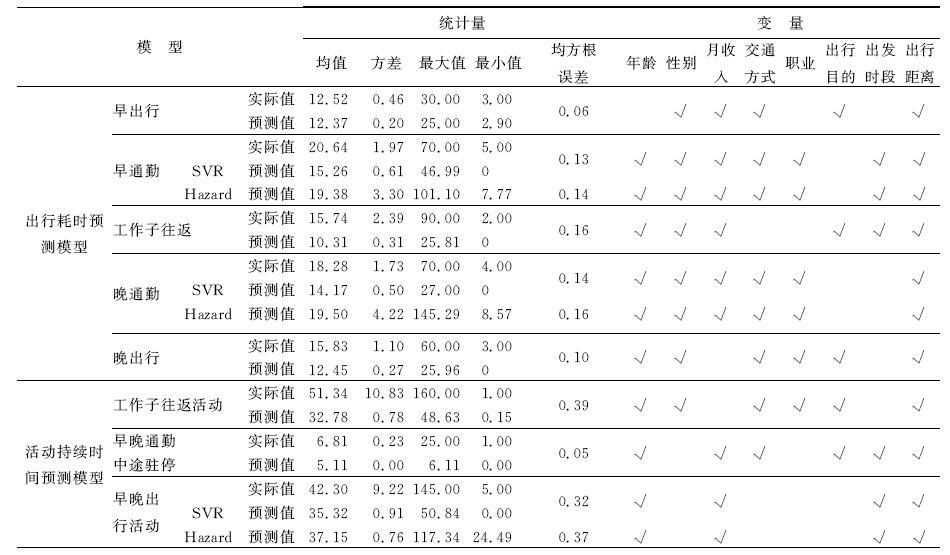
分别应用SVR和Hazard构建早通勤, 晚通勤出行耗时模型和早晚出行活动持续时间模型, 模型标定和预测结果如表2所示.对比二者的预测结果与真实值可知, SVR的预测结果比真实值更集中, 波动小, Hazard的预测结果更发散, 波动大.均方根误差计算结果表明, SVR的预测精度高于Hazard模型.可见, 在活动-出行连续时间预测方面, SVR优于Hazard模型, 因此选用SVR模型进行出行耗时和活动持续时间建模.

2.4 基于SVR的模型建立

基于SVR模型构建出行耗时和活动持续时间2组, 共8个模型, 各模型的标定结果见表2.均方根误差计算结果表明:各模型的预测精度均在可接受范围内[9], 早出行模型和早晚通勤中途驻停模型的预测精度较高, 而工作子往返和早晚出行活动持续时间模型的预测精度较低.另外, 各模型预测值均小于真实值, 预测结果比真实值分布更集中, 浮动小, 这一点也符合建模预测的基本规律.为了验证所建模型的可转移性, 应用已建立的模型, 代入2010年北京市居民出行调查数据, 进行通勤者的出行耗时和活动持续时间预测, 并将预测结果与实际值相对比.结果表明:在出行耗时预测中, 晚通勤的均方根误差最大, 为0.158; 在活动持续时间预测中, 工作子往返活动的均方根误差最大, 为0.382.两项误差均与表2所示的基于2006年出行调查数据的误差结果接近.这说明模型具有良好的稳定性和随时间可转移的特性.

从各模型涉及的变量来看, 出行距离在各个模型中均为显著影响变量, 说明出行距离是通勤者的出行耗时和活动持续时间决策中的一项重要因素.另外, 出行方式对工作子往返出行耗时及早晚出行的活动持续时间影响不显著.统计出行数据表明:工作子往返和早晚出行一般为短距离出行, 其中55.40%采取步行方式, 方式分布的不均衡可能是出行方式影响不显著的原因之一.此外, 出行目的对于早, 晚通勤出行耗时和早, 晚出行活动持续时间外的其他时间要素有影响.标定结果还说明出发时段对于出行耗时以及活动持续时间有影响.

表2 出行耗时和活动持续时间模型标定结果 Table 2 Estimation results of travel time and activity duration prediction models
3 模型应用

将已建的出行耗时预测模型应用于公交优先政策评价.选取数据库中家庭编号为0101* * * * 585到0102* * * * 853的150位通勤者的早出行, 早通勤, 工作子往返, 晚通勤和晚出行数据.统计得到这五类出行中的公交(含地铁)方式分担率分别为6.0%, 29.3%, 10.7%, 30.7%和9.3%.假设通过实施公交优先相关措施, 使五类出行的公交分担率均提高到50%, 将此值分别代入已建的5个出行耗时预测模型, 预测出行方式调整后的各段出行耗时, 并与真实值对比, 结果见表3.

表3 公交优先政策实施前后出行耗时对比表 Table 3 Prediction results of travel time affected by transit priority policy min

表3表明:公交出行比例提高后, 各段出行耗时的预测值明显低于真实值, 最高降低比例达到90%.说明公交优先政策可以有效减少居民的通勤出行耗时.

4 结束语

本研究基于活动链理论构建了通勤日活动-出行链, 给出了其中的主要时间要素, 对比分析了Hazard和SVR模型在活动-出行持续时间预测中的精度, 基于SVR模型建立了出行耗时预测模型和活动持续时间预测模型, 预测了通勤活动-出行链中各次出行的出行耗时以及各次活动的持续时间, 并应用出行耗时模型分析了公交优先策略对出行耗时的影响.研究表明, 所建模型能够以较高精度预测通勤者的日出行耗时和活动持续时间, 在连续的出行耗时预测中SVR的预测精度高于Hazard模型.研究结论可以为活动-出行行为的整体建模预测提供模型基础, 同时为掌握居民通勤出行规律, 考察相关交通管理政策的可行性提供决策分析工具.后续研究需继续考虑通勤日活动-出行时间系统中的离散时间要素的预测问题, 并研究如何构建通勤日活动-出行时间预测模型系统以及将其嵌入日活动-出行行为预测模型系统中.

The authors have declared that no competing interests exist.

参考文献
[1] 隽志才, 鲜于建川. 基于持续时间模型的日出行时间分析[J]. 交通运输系统工程与信息, 2010, 10(4): 62-67.
Juan Zhi-cai, Xianyu Jian-chuan. Daily travel time analysis with duration model[J]. Journal of Transportation System Engineering & Intelligent, 2010, 10(4): 62-67. [本文引用:2]
[2] Bhat C. Analysis of travel mode and departure time choice for urban shopping trips[J]. Transportation Research B, 1998, 32(6): 361-371. [本文引用:2]
[3] Small K A. The scheduling of consumer activities: work trips[J]. American Economic Review, 1982, 72(3): 467-479. [本文引用:2]
[4] Bhat C, Steed J. A continuous-time model of departure time choice for urban shopping trips[J]. Transportation Research, 2002, 36(3): 207-224. [本文引用:3]
[5] Pendyala R, Bhat C R. An exploration of the relati onship between timing and duration of maintenance activities[J]. Transportation, 2004, 31(4): 429-456. [本文引用:2]
[6] Zong Fang, Lin Hai-yun, Yu Bo, et al. Daily commute time prediction based on genetic algorithm[J]. Mathematical Problems in Engineering, 2012, doi: DOI:10.1155/2012/321574. [本文引用:2]
[7] 李福双. 智能公交车辆到站时间预测研究[D]. 北京: 北京交通大学交通运输学院, 2009.
Li Fu-shuang. Research on the prediction of intelligent bus arrival time[D]. Beijing: School of Traffic and Transportation, Beijing Jiaotong University, 2009. [本文引用:1]
[8] Vapnik V. The Nature of Statistical Learning Theory[M]. New York: Springer, 2000. [本文引用:1]
[9] 于滨, 蒋永雷, 于博, 等. 支持向量机在公交车辆运行时间预测中的应用[J]. 大连海事大学学报, 2008, 34(4): 158-160.
Yu Bin. Jiang Yong-lei, Yu Bo, et al. Application of support vector machines in bus travel time prediction[J]. Journal of Dalian Maritime University, 2008, 34(4): 158-160. [本文引用:2]