基于可靠度的动态随机交通网络耗时最优路径

引用本文

潘义勇, 马健霄, 孙璐. 基于可靠度的动态随机交通网络耗时最优路径.吉林大学学报:工学版, 2016, 46(2): 412-417
PAN Yi-yong, MA Jian-xiao, SUN Lu. Optimal path in dynamic network with random link travel times based on reliability. Journal of Jilin University Engineering and Technology Edition, 2016, 46(2): 412-417 复制到剪切板

Permissions

基于可靠度的动态随机交通网络耗时最优路径

潘义勇¹, 马健霄¹, 孙璐²

1.南京林业大学汽车与交通工程学院,南京 210037

2.美国Catholic大学土木工程系,美国华盛顿特区 20064

通讯作者:马健霄(1966-),男,教授,博士生导师.研究方向:交通管理与控制.E-mail:majx@njfu.edu.cn

作者简介:潘义勇(1980-),男,讲师,博士.研究方向:交通管理与控制.E-mail:uoupanyg@163.com

基金:国家自然科学基金重点项目(U1134206); 国家自然科学基金青年科学基金项目(51508280); 交通运输部西部项目(0901005C); 江苏省自然科学基金创新学者攀登计划项目(SBK200910046)

摘要

为了反映交通网络中考虑可靠性的路径选择行为,基于可靠性理论建立了动态随机网络环境下自适应最可靠路径模型.首先,定义行程时间可靠度为路径的目标函数,建立动态随机网络自适应最可靠路径模型反映交通网络的耗时随机特性,时变特性和风险性;其次,通过最优化理论把该问题转化为动态规划问题;然后,构造动态规划算法求解该问题;最后,通过Matlab计算机语言实现了算法程序,并针对实际交通网络展开数值试验.计算结果显示了该算法的收敛性和可行性.

关键词: 交通运输工程; 智能交通; 动态随机网络; 自适应路径; 可靠性; 动态规划

中图分类号:U491 文献标志码:A 文章编号:1671-5497(2016)02-0412-06

Optimal path in dynamic network with random link travel times based on reliability

PAN Yi-yong¹, MA Jian-xiao¹, SUN Lu²

1.College of Automobile and Traffic Engineering, Nanjing Forestry University, Nanjing 210037,China

2.Department of Civil Engineering,The Catholic University of America,Washington DC 20064,USA

Abstract

In order to reflect the routing selection behavior considering reliability in essence, a mathematic model of optimal-reliable routing in stochastic and dynamic traffic network is developed based on reliability theory. First, through defining reliability as the objective function of routing, the adaptive reliable shortest path problem in stochastic and dynamic network is established to reflect the stochastic, time-varying and risk characteristics of travel time. Then, using optimization theory, the adaptive reliable shortest path problem is transformed the dynamic programming problem. Finally, an algorithm based on dynamic programming is developed to solve the proposed problem. Numerical results in typical transportation network demonstrate the validity and feasibility of the proposed algorithm.

Keyword: engineering of communications and transportation; intelligent transportation; stochastic and dynamic network; adaptive path; reliability; dynamic programming

Show Figures

0 引言

耗时最优路径问题是智能交通系统(Intelligent transportation system, ITS)核心子系统之一的路径诱导系统(Route guidance system, RGS)的核心问题, 是交通工程研究热点领域^{[1, 2, 3]}.动态随机网络指网络边的权值不仅是随机变量, 而且该随机变量的概率分布函数是随时间变化的, 可以用来同时描述实际交通网络行程时间的时变特性和随机特性^[4].随机路径分为先验路径和自适应路径, 但是自适应路径比先验路径更优^[4].另一方面, 随着实时导航系统的发展和广泛应用, 在线的自适应路径问题越来越受到重视, 具有深刻的应用背景和重要的理论意义.

在动态随机网络环境下, 路径的最优性条件根据不同的需求有不同的定义, 主要分为期望值最小和可靠性最大.国内外学者主要研究最小期望路径问题, Miller-Hooks^{[5, 6]}假设动态随机网络中网络边的时间维和空间维都是独立的随机变量, 并构造了标号修正算法求解最小期望路径策略问题, 但是这种独立性的假设不满足实际交通网络的需要.Bander和White^[7]设计了启发式搜索方法AO* 求解自适应最小期望路径问题, 但是该算法不能保证收敛性.Gao^{[8, 9, 10]}讨论了自适应最小期望路径问题的几种近似问题, 并基于在线实时信息获取的不同情形对问题进行了分类, 提出了基于文献^{[5, 6]}DOT算法的DOT-SPI算法求解自适应最小期望路径问题.但是, 最小期望路径不能反映该路径的可靠性, 而对于风险规避的行驶者不仅关注行程时间的节省, 而且还关注行程时间的可靠性^{[11, 12, 13, 14, 15]}.把可靠度^[16]定义为路径目标函数以反映交通网络中考虑可靠性的路径选择行为, 文献^[17]研究了静态随机网络环境下最可靠路径问题, 本文是文献^[17]的后续研究, 把上述问题扩展到动态网络环境下, 研究动态随机交通网络环境下最可靠路径问题.

1 问题模型

动态随机网络 $G = (N, A, \tilde{X}, T), N (| N |= n)$ 是节点的集合, $A (| A |= m)$ 是边的集合.每个节点i都有若干前节点和后节点与之连接, 这些前节点的集合记为 $Φ (i) = {j, (i, j) \in A}$ , 后节点的集合记为 $Φ^{- 1} (i) = {k, (k, i) \in A}$ .边(i, j)的行程时间可以构造为离散形式的随机过程 ${{\tilde{X}}_{ij} (t), t \in T}$ , T是出发时间的离散点集合.边(i, j)在出发时间t∈ T的行程时间是独立的随机变量 ${\tilde{X}}_{ij} (t)$ , 该随机变量的可能取值是有限个支撑点 $(X_{ij}^{1} (t), X_{ij}^{2} (t), \dots, X_{ij}^{R_{ij} (t)} (t))$ , 其中R_ij (t)为支撑点的总个数.第r个支撑点取值的概率为 $p_{ij}^{r} (t)$ , 并且 $\overset{R_{ij} (t)}{\sum_{r = 1}} p_{ij}^{r} (t) = 1$ . $X_{ij}^{r} (t)$ 表示随机变量 ${\tilde{X}}_{ij} (t)$ 取r支撑点, 其相应的概率为 $p_{ij}^{r} (t)$ .在本文中, 上标"~"是表示随机变量, 不含"~"表示该随机变量的具体取值.

自适应路径并不是严格上的一条路, 是一个自适应路径策略的集合, 决策者根据当前的行车状态x_i=(i, t, b) 选择下一个节点, 其中i为当前节点, t为当前时刻, b∈ B为当前的行程时间预算.定义集合N, T和B的笛卡尔积的集合Ω =N× T× B, 自适应路径策略是一个函数μ :Ω → N, μ (i, t, b)表示根据当前的行车状态选择的下一个节点.行驶者根据自适应路径策略μ :Ω → N选择的下一个节点是j, 下一个节点的当前状态 $x_{j} = {j, \tilde{t}, \tilde{b}}$ 是不确定的, 例如随机变量 $\tilde{t}, \tilde{b}$ .边(i, j)的行程时间 ${\tilde{X}}_{ij} (t)$ 是随机变量, 所以到达下一个节点j的时刻 $\tilde{t} = t - {\tilde{X}}_{ij} (t)$ 和行程时间预算 $\tilde{b} = b - {\tilde{X}}_{ij} (t)$ 也是随机变量.决策者根据自适应路径策略μ :Ω → N在行程中所经历的状态时间序列为 $μ^{od} = {x_{o}, \dots, x_{i}, x_{j}, \dots, x_{d}}$ , 称为自适应路径, 自适应路径并不是严格上的一条路, 是依据自适应路径策略所经历的状态集合.给定起始状态x_o=(o, t, b)和自适应路径策略μ :Ω → N, 起点和终点之间的行程时间为随机变量 ${\tilde{S}}_{μ}^{od}$ .终点的当前状态 $x_{d} = (d, \tilde{t}, \tilde{b})$ 是不确定的, 到达终点的时刻 $\tilde{t} = t + {\tilde{S}}_{μ}^{od}$ 和终点的行程时间预算 $\tilde{b} = b - {\tilde{S}}_{μ}^{od}$ 是随机变量.

设 $U_{μ} (x_{o}) = P ({\tilde{S}}_{μ}^{od} (t) \leq b)$ 为事件 ${\tilde{S}}_{μ}^{od} (t) \leq b$ 发生的概率, 则动态随机网络自适应最可靠路径问题定义为:

$\begin{matrix} U_{μ}^{*} (x_{o}) = \max {P ({\tilde{S}}_{μ}^{od} (t) \leq b), \forall μ} \end{matrix}$ (1)

$\begin{matrix} μ^{*} (x_{o}) = \arg \max {P ({\tilde{S}}_{μ}^{od} (t) \leq b), \forall μ} \end{matrix}$ (2)

2 动态规划

下面把动态随机网络自适应最可靠路径问题(1)(2)转化为动态规划问题求解, 证明其满足动态规划的Bellman's准则^[18].首先定义自适应最可靠路径策略和自适应最可靠路径.

定义1((t, b)-自适应最可靠路径策略) 给定出发时间t和行程时间预算b, 路径策略μ ^*是(t, b)-自适应最可靠路径策略当且仅当

$\begin{matrix} \begin{matrix} μ^{*} (i, t + x, b - x) = \\ \arg \max {U_{μ} (i, t + x, b - x), \forall μ} \\ \forall i \in N, x \in [0, b) \end{matrix} \end{matrix}$

定义2((t, b)-自适应最可靠路径) 依据(t, b)-自适应最可靠路径策略μ ^*所构成的自适应路径{x_u, x_j, , et al., x_d}称为(t, b)-自适应最可靠路径.

下面证明自适应最可靠路径满足动态规划的Bellman's准则^[18].

定理1 (t, b)-自适应最可靠路径的任意子路径都是(t, b)-自适应最可靠路径.

证明假设{x_i, x_j, , et al., x_d}是(t, b)-自适应最可靠路径, 并且它的子路径{x_j, , et al., x_d}不是(t, b)-自适应最可靠路径.因此, 存在路径策略μ '使得对某一个x∈ [0, b), $U_{μ}^{*} (j, t + x, b - x) < {U^{'}}_{μ} (j, t + x, b - x)$ .定义 $U_{μ} (x_{i}) = P ({\tilde{S}}_{μ}^{id} (t) \leq b)$ 表示当初始状态是x_i={i, t, b}时采用自适应路径策略μ 到达终点的概率, 则下一个节点的状态 $x_{j} = {j, \tilde{t}, \tilde{b}} = {j, t + {\tilde{X}}_{ij} (t), b - {\tilde{X}}_{ij} (t)}$ 是不确定的.定义 $P (X_{ij}^{r} (t))$ 为事件 ${\tilde{X}}_{ij} (t) = X_{ij}^{r} (t)$ 发生的概率.t和 $\tilde{t}$ , b和 $\tilde{b}$ , ${\tilde{S}}_{μ}^{id} (t)$ 和 ${\tilde{S}}_{μ}^{jd} (\tilde{t})$ 的关系为:

$\tilde{t} = t + {\tilde{X}}_{ij} (t), \tilde{b} = b - {\tilde{X}}_{ij} (t)$ (3)

${\tilde{S}}_{μ}^{jd} (t) = {\tilde{X}}_{ij} (t) + {\tilde{S}}_{μ}^{jd} (t) (t + {\tilde{X}}_{ij} (t))$ (4)

因此

$\begin{matrix} \begin{matrix} U_{μ} (x_{i}) = U_{μ} (i, t, b) = P ({\tilde{S}}_{μ}^{id} (t) \leq b) = \\ \sum_{r | X_{ij}^{r} (t) \leq b} P (X_{ij}^{r} (t)) \times P (X_{ij}^{r} (t) + {\tilde{S}}_{μ}^{id} (t + X_{ij}^{r} (t)) \leq b) = \\ \sum_{r | X_{ij}^{r} (t) \leq b} P (X_{ij}^{r} (t)) \times P ({\tilde{S}}_{μ}^{jd} (t + X_{ij}^{r} (t)) \leq b - X_{ij}^{r} (t)) = \\ \sum_{r | X_{ij}^{r} (t) \leq b} P (X_{ij}^{r} (t)) \times U_{μ} (j, t + X_{ij}^{r} (t), b - X_{ij}^{r} (t)) \end{matrix} \end{matrix}$ (5)

因为对某些 $\begin{matrix} X_{ij}^{r} (t), U_{μ}^{*} (j, t + X_{ij}^{r} (t), b - X_{ij}^{r} (t)) < U'_{μ} (j, t + X_{ij}^{r} (t), b - X_{ij}^{r} (t)), \end{matrix}$ 所以有:

$\begin{matrix} \begin{matrix} U_{μ}^{*} = \\ \sum_{r | X_{ij}^{r} (t) \leq b} P (X_{ij}^{r} (t)) \times U_{μ}^{*} (j, t + X_{ij}^{r} (t), b - X_{ij}^{r} (t)) < \\ \sum_{r | X_{ij}^{r} (t) \leq b} P (X_{ij}^{r} (t)) \times U'_{μ} (j, t + X_{ij}^{r} (t), b - X_{ij}^{r} (t)) = \\ U'_{μ} (x_{i}) \end{matrix} \end{matrix}$ (6)

这与假设{x_i, x_j, , et al., x_d}是(t, b)-自适应最可靠路径矛盾.

根据定理1, 动态随机网络环境下自适应最可靠路径问题满足动态规划Bellman's准则^[18], 因此, 给定出发时间t和时间预算b, 动态随机网络环境下自适应最可靠路径问题可以转化为下列动态规划问题:

$\begin{matrix} \begin{matrix} U_{μ}^{*} (i, t + x, b - x) = \\ \max_{j \in Φ (i)} {\sum_{r | X_{ij}^{r} (t + x) \leq b - x} P (X_{ij}^{r} (t + x)) \times \\ U_{μ}^{*} (j, t + x + X_{ij}^{r} (t), b - x - X_{ij}^{r} (t))} \\ \forall i \neq d, x \in [0, b) (7) \\ μ^{*} (i, t + x, b - x) = \\ \underset{j \in Φ (i)}{\arg \max} {\sum_{r | X_{ij}^{r} (t + x) \leq b - x} P (X_{ij}^{r} (t + x)) \times \\ U_{μ}^{*} (j, t + x + X_{ij}^{r} (t), b - x - X_{ij}^{r} (t))} \\ \forall i \neq d, x \in [0, b) (8) \\ U_{μ}^{*} (d, t + x, b - x) = 1, \forall x \in [0, b) \\ μ^{*} (d, t + x, b - x) = d, \forall x \in [0, b) \end{matrix} \end{matrix}$

下面构造基于动态规划的算法求解上述动态规划问题(7)和(8).给定出发时间t和行程时间预算b, 寻找(t, b)-自适应最可靠路径策略 $μ^{*} (i, t, b)$ .算法在第k次迭代时, $U_{μ}^{k} (i, t + x, b - x)$ 表示根据路径策略μ , t+x时刻从起点i出发在行程时间b-x内到达终点的概率, 并且该路径包含不超过k条边. $μ^{k} (i, t + x, b - x)$ 表示与 $U_{μ}^{k} (i, t + x, b - x)$ 相对应的下一个节点. $U_{μ}^{k} (i, t + x, b - x)$ 随着k的增大逼近最优值 $U_{μ}^{*} (i, t + x, b - x)$ , 当k的取值是最优路径所包含的边的条数时有:

$\begin{matrix} U_{μ}^{k} (i, t + x, b - x) = U_{μ}^{*} (i, t + x, b - x) \end{matrix}$

算法如下:

Step 0 初始化

0.1输入出发时间t, 行程时间预算b.

0.2初始化

k=0

For ∀ i∈ N, i≠ d, ∀ x∈ [0, b)

$\begin{matrix} U_{μ}^{k} \end{matrix}$ (i, t+x, b-x)=0

μ ^*(i, t+x, b-x)=φ

End for

$\begin{matrix} U_{μ}^{k} \end{matrix}$ (d, t+x, b-x)=1, ∀ x∈ [0, b)

μ ^*(d, t+x, b-x)=d, ∀ x∈ [0, b)

Step 1 迭代

k=k+1

1.1 终点迭代

$\begin{matrix} U_{μ}^{k} \end{matrix}$ (d, t+x, b-x)=1, ∀ x∈ [0, b)

μ ^*(d, t+x, b-x)=d, ∀ x∈ [0, b)

1.2 其他节点迭代

For ∀ i≠ N, i≠ d, ∀ x∈ [0, b)

$\begin{matrix} U_{μ}^{k} \end{matrix} (i, t + x, b - x) = \begin{matrix} \max_{j \in Φ (i)} \end{matrix} [\begin{matrix} \sum_{r | X_{ij}^{r} (t + x) \leq b - x} \end{matrix} P (\begin{matrix} X_{ij}^{r} \end{matrix} (t + x)) \times \begin{matrix} U_{μ}^{k - 1} \end{matrix} (j, t + x + \begin{matrix} X_{ij}^{r} \end{matrix} (t + x), b - x - \begin{matrix} X_{ij}^{r} \end{matrix} (t + x))]$

μ ^k(i, t+x, b-x)=

$\begin{matrix} \max_{j \in Φ (i)} \end{matrix} [\begin{matrix} \sum_{r | X_{ij}^{r} (t + x) \leq b - x} \end{matrix} P (\begin{matrix} X_{ij}^{r} \end{matrix} (t + x)) \times \begin{matrix} U_{μ}^{k - 1} \end{matrix} (j, t + x + \begin{matrix} X_{ij}^{r} \end{matrix} (t + x), b - x - \begin{matrix} X_{ij}^{r} \end{matrix} (t + x))]$

End for

Step 2 收敛性判定

If ∀ i≠ N, ∀ x∈ [0, b)

max $\begin{matrix} |U_{μ}^{k} (i, t + x, b - x) - U_{μ}^{k - 1} (i, t + x, b - x)| \end{matrix}$ =0 stop;

Otherwise go to step 1.

3 数值试验

本文采用实际交通网络的拓扑结构Sioux Falls(SF)network^[17].这有利于数值试验符合实际的交通状况, 有利于下一步的应用研究.所有算法都是通过Matlab计算机语言编程并且在Windows-XP(64)工作站(two 2.00 GHz Xeon CPUs and 4G RAM)条件下运行的.另外, 由于实际交通流数据采集的困难和缺失, 为了模拟实际交通网络中每个路段的行程时间采集的离散数据, 假设交通网络中每个路段的行程时间采集离散数据符合Gamma概率分布函数, 这也是符合实际交通网络行程时间的概率分布函数, 当然也可以假设其他的概率分布函数, 因为本算法针对的是交通网络行程时间的任意概率分布函数, 交通网络边的行程时间的概率分布函数的不同设定不影响验证算法的可行性和正确性.

边的随机行程时间 $\begin{matrix} {\tilde{X}}_{ij} (t) \end{matrix}$ 服从以下的Gamma分布Gamma $\begin{matrix} (α_{ij} (t), β_{ij} (t)) : \end{matrix}$

$f_{ij} (t, x) = \frac{(β_{ij} {(t))}^{α_{ij} (t)} x^{α_{ij} (t) - 1} e^{β_{ij} (t) x}}{Γ (α_{ij} (t))}$ (9)

式中

$\begin{matrix} α_{ij} (t) = 0.4 g (t) \lg (10 + 0.8 i + 0.7 j) \\ β_{ij} (t) = 2 g (t) \lg (12 + 1.2 i + 0.8 j) \\ g (t) = \{\begin{matrix} 1, 0 \leq t \leq 3 \\ 1, 3 \leq t \leq 6 \\ 2.5, t > 6 \end{matrix} \end{matrix}$

$\begin{matrix} g (t) \end{matrix}$ 是一个阶段函数.Gamma分布的期望值和方差分别是 $\begin{matrix} α_{ij} (t) / β_{ij} (t) 和 α_{ij} (t \frac{)}{(} β_{ij} {(t))}^{2} 。 \end{matrix}$

为了模拟离散型动态随机网络模型, 设b=Lϕ 是行程时间预算, 其中ϕ 为划分的时间单元.这里取ϕ =2.对于任意的边(i, j), 随机行程时间 ${\tilde{X}}_{ij} (t)$ 的概率质量函数P_ij (t, x)可以通过概率密度函数f_ij (t, x)获得, 如下式所示:

$\begin{matrix} \begin{matrix} P_{ij} (t, x) = \\ \{\begin{matrix} \int_{x}^{x} f_{ij} (t, w) dw, x = 0, ϕ, 2 ϕ, \dots, (L - 1) ϕ \\ \int_{x}^{\infty} f_{ij} (t, w) dw, x = Lϕ \\ 0, ot h erwise \end{matrix} \end{matrix} \end{matrix}$ (10)

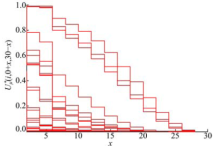
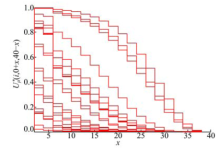
上述定义假设随机变量 $\begin{matrix} {\tilde{X}}_{ij} (t) \end{matrix}$ 的取值只能是ϕ 的倍数, 则:

$\begin{matrix} \begin{matrix} U_{μ} (i, t + x, b - x) = \overset{b - x}{\sum_{y = 0}} P_{ij} (t + x, y) \times \\ U_{μ} (j, t + x + y, b - x - y) \\ \forall x = 0, ϕ, 2 ϕ, \dots; Lϕ = b \end{matrix} \end{matrix}$ (11)

图1表示从节点i=1, 2, , et al., 24(i≠ 18)在t+x(t=0)时刻出发在b-x(b=30)时间内到达终点N=18的最大概率值 $U_{μ}^{*} (i, t + x, b - x)$ 关于x的函数图.图2表示从节点i=1, 2, , et al., 24(i≠ 18)在t+x(t=0)时刻出发在b-x(b=40)时间内到达终点N=18的最大概率值 $U_{μ}^{*} (i, t + x, b - x)$ 关于x的函数图.

	Figure Option View Download New Window
	图1 $\begin{matrix} U_{μ}^{} \end{matrix}$ (i, 0+x, 30-x)关于x的变化图Fig.1* $\begin{matrix} U_{μ}^{*} \end{matrix}$ (i, 0+x, 30-x) following the x

	Figure Option View Download New Window
	图2 $\begin{matrix} U_{μ}^{} \end{matrix}$ (i, 0+x, 40-x)关于x的变化图Fig.2* $\begin{matrix} U_{μ}^{*} \end{matrix}$ (i, 0+x, 40-x) following the x

计算结果表明:

(1)因为数值实验中采用了离散型的随机变量, 所以函数 $U_{μ}^{*} (i, t + x, b - x)$ 是一个阶梯函数, 并且是关于x的单调递减函数, 这符合在动态随机网络满足随机一致先进先出准则的情况下, $U_{μ}^{*} (i, t + x, b - x)$ 关于x的单调递减函数的性质.

(2)因为本文采用的分段时段的概率分布函数表达式参数取值是不同的, 所以函数 $\begin{matrix} U_{μ}^{*} (i, t + x, b - x) \end{matrix}$ 关于x的单调递减函数在t取值为时间分段点会有一个大的波动.

(3)函数 $U_{μ}^{*} (i, t + x, b - x)$ 的取值与起点, 终点, 时间预算b, 出发时间t和x的取值都有关, 是一个多元函数.函数 $U_{μ}^{*} (i, t + x, b - x)$ 在起点和终点一定的情况下的取值不仅取决于起点的出发时间t, 而且还取决于时间预算b.对于同样的出发时间t, 不同时间预算b对应的函数 $U_{μ}^{*} (i, t + x, b - x)$ 的取值是不同的, 同样, 对于相同的时间预算b, 不同出发时间t对应的函数 $U_{μ}^{*} (i, t + x, b - x)$ 的取值也不同; 对于给定的起点和终点, 时间预算b和出发时间t, 函数 $U_{μ}^{*} (i, t + x, b - x)$ 的取值与x有关.

(4)起点离终点越远, 则相应的 $U_{μ}^{*} (i, t + x, b - x)$ 的函数值越小.相反, 起点离终点越近, 则相应的 $U_{μ}^{*} (i, t + x, b - x)$ 的函数值越大.当终点一致, 起点邻近时, 相应的 $U_{μ}^{*} (i, t + x, b - x)$ 取值非常接近, 因此图中相邻点的 $U_{μ}^{*} (i, t + x, b - x)$ 关于x的函数曲线图有一定的重合.这与理论分析是一致的.

(5)起点离终点越远, 则相应的概率 $U_{μ}^{*} (i, t + x, b - x)$ 取值越低, 甚至为零.当函数 $U_{μ}^{*} (i, t + x, b - x)$ 取值为零时, 算法不能判断最优解, 无法给出自适应最可靠路径.

4 结束语

针对交通网络中考虑风险的路径选择行为, 基于可靠性理论, 定义行程时间可靠度为路径的目标函数, 建立动态随机网络环境下最可靠路径模型.通过最优化理论把该问题转化为动态规划问题求解, 通过对实际交通网络的计算对提出的算法进行了验证.计算结果表明, 给定起始时间和预算时间, 本文算法可以获得动态随机网络自适应最可靠路径, 研究结果可为智能交通系统路径诱导子系统提供理论支撑和核心技术, 是对运筹学理论研究的扩展, 具有深刻的应用背景和重要的理论意义.

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	黄卫, 张宁. 智能交通系统理论研究与实践[M]. 南京: 江苏科学技术出版社, 2011. [本文引用:1]
[2]	杨兆升. 城市交通流诱导系统理论与模型[M]. 北京: 人民交通出版社, 2000. [本文引用:1]
[3]	Schrank D, Lomax T. The 2012 annual urban mobility report[R]. Texas: Texas Transportation Institute, The Texas A&M University, 2012. [本文引用:1]
[4]	Hall R W. The fastest path through a network with rand om time-dependent travel times[J]. Transportation Science, 1986, 20(3): 182-188. [本文引用:2]
[5]	Miller-Hooks E D. Optimal routing in time-varying, stochastic networks: algorithms and implementations[D]. Austin: The University of Texas at Austin, 1997. [本文引用:2]
[6]	Miller-Hooks E. Adaptive least-expected time paths in stochastic, time-varying transportation and data networks[J]. Networks, 2001, 37(1): 35-52. [本文引用:2]
[7]	Band er J L, White C C. A heuristic search approach for a nonstationary stochastic shortest path problem with terminal cost[J]. Transportation Science, 2002, 36(2): 218-230. [本文引用:1]
[8]	Gao S, Chabini I. Optimal routing policy problems in stochastic time-dependent networks[J]. Transportation Research Part B: Methodological, 2006, 40(2): 93-122. [本文引用:1]
[9]	Gao S, Huang H. Real-time traveler information for optimal adaptive routing in stochastic time-dependent networks[J]. Transportation Research Part C: Emerging Technologies, 2012, 21(1): 196-213. [本文引用:1]
[10]	Huang H, Gao S. Optimal paths in dynamic networks with dependent rand om link travel times[J]. Transportation Research Part B: Methodological, 2012, 46(5): 579-598. [本文引用:1]
[11]	Wu X, Nie Y. Modeling heterogeneous risk-taking behavior in route choice: a stochastic dominance approach[J]. Transportation Research Part A, 2011, 45: 896-915. [本文引用:1]
[12]	Chen B Y, Lam W H K, Sumalee A, et al. Finding reliable shortest paths in road networks under uncertainty[J]. Networks and Spatial Economics, 2013, 13(2): 123-148. [本文引用:1]
[13]	Chen B Y, Lam W H K, Sumalee A, et al. Reliable shortest path finding in stochastic networks with spatial correlated link travel times[J]. International Journal of Geographical Information Science, 2012, 26(2): 365-386. [本文引用:1]
[14]	Ramaekers K, Reumers S, Wets G, et al. Modelling route choice decisions of car travellers using combined GPS and diary data[J]. Networks and Spatial Economics, 2013, 13(3): 351-372. [本文引用:1]
[15]	Yao B, Hu P, Lu X, et al. Transit network design based on travel time reliability[J]. Transportation Research Part C: Emerging Technologies, 2014, in Press. [本文引用:1]
[16]	张志华. 可靠性理论及工程应用[M]. 北京: 科学出版社, 2012. [本文引用:1]
[17]	潘义勇, 孙璐. 随机交通网络环境下自适应最可靠路径问题[J]. 吉林大学学报: 工学版, 2014, 44(6): 1622-1627. Pan Yi-yong, Sun Lu. Adaptive reliable shortest path problem in stochastic traffic net work[J]. Journal of Jilin University(Engineering and Technology Edition), 2014, 44(6): 1622-1627. [本文引用:3]
[18]	党耀国, 朱建军, 李帮义, 等. 运筹学[M]. 北京: 科学出版社, 2012. [本文引用:3]

2011

0.0

... 0 引言耗时最优路径问题是智能交通系统(Intelligent transportation system,ITS)核心子系统之一的路径诱导系统(Route guidance system,RGS)的核心问题,是交通工程研究热点领域^[1,2,3] ...

2000

0.0

2012

0.0

1986

0.0

... 动态随机网络指网络边的权值不仅是随机变量,而且该随机变量的概率分布函数是随时间变化的,可以用来同时描述实际交通网络行程时间的时变特性和随机特性^[4] ...

... 随机路径分为先验路径和自适应路径,但是自适应路径比先验路径更优^[4] ...

1997

0.0

... 国内外学者主要研究最小期望路径问题,Miller-Hooks^[5,6]假设动态随机网络中网络边的时间维和空间维都是独立的随机变量,并构造了标号修正算法求解最小期望路径策略问题,但是这种独立性的假设不满足实际交通网络的需要 ...

... Gao^[8,9,10]讨论了自适应最小期望路径问题的几种近似问题,并基于在线实时信息获取的不同情形对问题进行了分类,提出了基于文献^[5,6]DOT算法的DOT-SPI算法求解自适应最小期望路径问题 ...

2001

0.0

2002

0.0

... Bander和White^[7]设计了启发式搜索方法AO#cod#x0002A ...

2006

0.0

2012

0.0

2012

0.0

2011

0.0