集中力作用下考虑剪切滑移效应的双层结合面组合梁解析解

引用本文

郭学东, 马立军, 张云龙. 集中力作用下考虑剪切滑移效应的双层结合面组合梁解析解.吉林大学学报:工学版, 2016, 46(2): 432-438
GUO Xue-dong, MA Li-jun, ZHANG Yun-long. Analytical solution of the double joint layer composite beam with shear-slip under vertical concentrated load. Journal of Jilin University Engineering and Technology Edition, 2016, 46(2): 432-438 复制到剪切板

Permissions

集中力作用下考虑剪切滑移效应的双层结合面组合梁解析解

郭学东¹, 马立军^1,², 张云龙²

1.吉林大学交通学院,长春 130022

2.吉林建筑大学交通科学与工程学院,长春 130118

通讯作者:张云龙( 1975-),男, 副教授.研究方向:道路与桥梁工程计算理论.E-mail:zyl_ql@163.com

作者简介:郭学东(1955-),男,教授,博士生导师.研究方向:桥梁加固与检测.E-mail:ypyc@jlu.edu.com

基金:国家自然科学基金项目(51308256)

摘要

为了分析碳纤维-钢-混凝土组合梁在竖向集中荷载作用下的静力响应,基于弹性力学的经典理论,推导了竖向集中力作用下的双层结合面组合梁的解析解,得到了碳纤维-钢-混凝土双层结合面组合梁的挠曲线方程,并通过具体算例与有无相互作用的组合梁计算结果进行了对比,结果表明该解析解是正确的,合理的,为工程设计人员提供了一种可靠的设计计算方法,具有较强的实际应用价值.

关键词: 土木工程; 碳纤维-钢-混凝土; 双层结合面组合梁; 滑移

中图分类号:TU311.1 文献标志码:A 文章编号:1671-5497(2016)02-0432-07

Analytical solution of the double joint layer composite beam with shear-slip under vertical concentrated load

GUO Xue-dong¹, MA Li-jun^1,², ZHANG Yun-long²

1.College of Transportation, Jilin University,Changchun 130022,China

2.School of Transportation Science and Engineering, Jilin Jianzhu University, Changchun 130118, China

Abstract

In order to analyze the static response of the carbon fiber-steel-concrete composite beams under vertical concentrated load, an analytical solution of the double joint layer composite beams under vertical concentrated load was derived. This analytical solution is based on classical theory of elasticity. The equation of deflection curve of the carbon fiber-steel-concrete double joint layer composite beams was obtained. Numerical calculations of the composite beams with or without interaction are carried out to compare the effect of interaction. The results demonstrate that the analytical solution is correct and reasonable, which provides the engineering designers with a reliable calculation method and has strong practical value.

Keyword: civil engineering; carbon fiber-steel-concrete; double joint layer composite beam; slip

Show Figures

0 引言

组合梁是将具有不同力学性能的材料组合在一起, 能将各自性能充分发挥出来的一种梁.由于该种结构具有质量轻, 承载力大, 跨越能力强, 施工方便等优点^{[1, 2, 3, 4, 5]}, 对有高度及跨度要求的建筑采用组合梁比较合适.近些年组合梁应用于公路及城市桥梁工程中比较普遍, 因此, 有关组合梁理论及试验研究也成为土木工程领域的研究热点之一^{[6, 7, 8, 9]}.目前较为常用的组合梁由抗压能力强的混凝土和抗拉能力强的钢两层材料组成.随着碳纤维技术的逐渐成熟, 在组合梁的受拉区采用碳纤维板材代替钢梁的底板, 形成具有双层结合面的新型组合梁结构形式, 不失为一种理想的方案, 但由于双层结合面组合梁是三种材料组合而成, 具有两层结合面, 其变形不再符合平截面假定, 当考虑结合面的滑移效应时, 相对常规组合梁(两种材料组成的组合梁)而言, 其力学状态复杂得多, 应力及变形未知量增多, 很难寻找到符合实际的边界条件, 求解难度成倍增加, 目前还无此种组合梁的精确计算方法.本文以碳纤维-钢-混凝土三种材料结合的具有双层结合面的组合梁为研究对象, 基于弹性力学方法, 推导了集中力作用下考虑两层交界面剪切滑移效应的简支组合梁挠曲线方程, 并给出了对应的滑移曲线.

1 基本假定

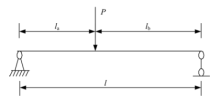
根据图1所示的双层结合面组合梁在使用阶段的受力特性, 为便于问题的分析, 本文采用的基本假设如下:① 碳纤维板, 钢梁, 混凝土板均视为均质连续弹性体; ② 各结合面存在剪切滑移, 剪切力与滑移量成正比; ③ 混凝土板及钢梁自身满足平截面假定, 且同一截面三者竖向位移及转角相等; ④ 碳纤维板与钢梁之间, 混凝土板与钢梁之间均无掀起.

	Figure Option View Download New Window
	图1 双层结合面组合梁Fig.1 Double joint layer composite beam

2 双层结合面组合梁挠曲线方程

2.1 双层结合面组合梁位移函数

	Figure Option View Download New Window
	图2 简支梁受力图示Fig.2 Force shown of simply supported beam

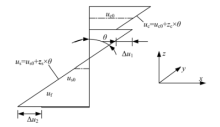
根据图2给出的简支梁受力图, 基于弹性力学的经典理论, 可得出碳纤维-钢-混凝土组合梁的位移函数为: $u_{c} (x, z_{c}) 、 u_{s} (x, z_{s}) 、 u_{f} (x) 、 w (x)$ , 其中 $u_{c} (x, z_{c}) 、 u_{s} (x, z_{s}) 、 u_{f} (x)$ 分别为截面x处混凝土顶板, 钢梁和碳纤维底板的轴向位移, $\begin{matrix} w (x) \end{matrix}$ 为组合梁竖向位移, 由于不考虑组合梁的竖向掀起效应, $\begin{matrix} w (x) = w_{c} (x) = w_{s} (x) = w_{f} (x) 。 \end{matrix}$

	Figure Option View Download New Window
	图3 组合梁横断面位移图示Fig.3 Composite beam cross-sectional shown of displacement

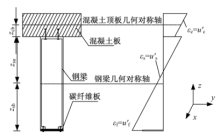
根据图3, 可给出双层结合面组合梁的位移函数式为:

$\begin{matrix} \{\begin{matrix} u_{c} (x, z_{c}) = u_{c 0} (x) + z_{c} θ (x) \\ w (x) = w (x) \\ u_{s} (x, z_{s}) = u_{s 0} (x) + z_{s} θ (x) \\ u_{f} (x) = u_{f} (x) \end{matrix} \end{matrix}$ (1)

式中: $\begin{matrix} u_{c 0} (x) \end{matrix}$ 为混凝土截面几何对称轴处轴向位移; $\begin{matrix} u_{s 0} (x) \end{matrix}$ 为钢梁截面几何对称轴处轴向位移; $\begin{matrix} θ (x) = w' (x) \end{matrix}$ 为截面x处转角; z_c为混凝土顶板各点距混凝土截面几何对称轴处的距离矢量; $\begin{matrix} z_{s} \end{matrix}$ 为钢梁各点距钢梁截面几何对称轴处的距离矢量.

令 $\begin{matrix} Δ u_{1} 、 Δ u_{2} \end{matrix}$ 分别为上下两层结合面处滑移位移差, 根据式(1)可得:

$\begin{matrix} \begin{matrix} Δ u_{1} (x) = u_{cb} (x) - u_{su} (x) = [u_{c 0} (x) - u_{s 0} (x)] - z_{d} θ (x) \end{matrix} \end{matrix}$ (2)

式中: $\begin{matrix} u_{cb} (x) \end{matrix}$ 为混凝土顶板底缘轴向位移, $\begin{matrix} u_{su} (x) \end{matrix}$ 为钢梁顶面轴向位移, $\begin{matrix} z_{d} = z_{cb} + z_{su} 。 \end{matrix}$

$\begin{matrix} \begin{matrix} Δ u_{2} (x) = u_{sb} (x) - u_{f} (x) = [u_{s 0} (x) - u_{f} (x)] - z_{sb} θ (x) \end{matrix} \end{matrix}$ (3)

式中: $\begin{matrix} u_{f} (x) \end{matrix}$ 为碳纤维板轴向位移; $\begin{matrix} u_{sb} (x) \end{matrix}$ 为钢梁底面轴向位移.

2.2 双层结合面组合梁几何方程

由弹性力学可知, 如图4所示, 各部分位移与应变之间的关系为:

$\begin{matrix} \{\begin{matrix} ε_{c} (x) = u'_{c} (x) \\ ε_{s} (x) = u'_{s} (x) \\ ε_{f} (x) = u'_{f} (x) \\ θ (x) = w' (x) \\ k (x) = w ″ (x) \end{matrix} \end{matrix}$ (4)

式中: $\begin{matrix} ε_{c} (x) 、 ε_{s} (x) 、 ε_{f} (x) \end{matrix}$ 分别为混凝土应变, 钢梁应变及碳纤维板应变; $\begin{matrix} k (x) 为截面 x \end{matrix}$ 处曲率, 为挠度的二阶导数.

	Figure Option View Download New Window
	图4 组合梁各部分应变分布Fig.4 Composite Beams strain distribution

2.3 双层结合面组合梁的物理方程

(1)层间剪切集度与剪切滑移量之间的关系

由文献^[5]可知:

$\begin{matrix} [\begin{matrix} q_{1} \\ q_{2} \end{matrix}] = [\begin{matrix} k_{s} Δ u_{1} / l_{s} \\ k_{f} Δ u_{2} / l_{f} \end{matrix}] \end{matrix}$ (5)

式中: $\begin{matrix} q_{1} 、 q_{2} \end{matrix}$ 分别为混凝土与钢梁结合面处剪切应力集度和钢梁与碳纤维板结合面处剪切应力集度; $\begin{matrix} k_{s} 、 k_{f} \end{matrix}$ 分别为上下两层剪切刚度; $\begin{matrix} l_{s} 、 l_{f} \end{matrix}$ 分别为上下两层剪力连接件距离.

(2)各部分内力与应变之间的关系

$\begin{matrix} \{\begin{matrix} N_{c} (x) = A_{c} σ_{c} (x) = E_{c} A_{c} ε_{c} (x) \\ N_{s} (x) = A_{s} σ_{s} (x) = E_{s} A_{s} ε_{s} (x) \\ N_{f} (x) = A_{f} σ_{f} (x) = E_{f} A_{f} ε_{f} (x) \\ M_{c} (x) = E_{c} I_{c} k (x) \\ M_{s} (x) = E_{s} I_{s} k (x) \end{matrix} \end{matrix}$ (6)

式中: $\begin{matrix} E_{c} 、 E_{s} 、 E_{f} \end{matrix}$ 分别为混凝土, 钢材, 碳纤维的弹性模量; $\begin{matrix} A_{c} 、 A_{s} 、 A_{f} \end{matrix}$ 分别为混凝土顶板, 钢梁, 碳纤维底板的横断面面积; $\begin{matrix} I_{c} 、 I_{s} \end{matrix}$ 分别为混凝土顶板, 钢梁的抗弯惯性矩.

2.4 双层结合面组合梁的平衡方程

根据文献[2]给出的交界面剪力集度与轴力的关系和式(4)(6)可知:

$\begin{matrix} \{\begin{matrix} q_{1} = N'_{c} (x) = E_{s} A_{c} u ″_{c} (x) \\ q_{2} = N'_{f} (x) = - E_{f} A_{f} u ″_{f} (x) \end{matrix} \end{matrix}$ (7)

由图2所示的简支梁和图4给出的应变分布, 依据内外力之间的平衡关系可知:在外力 $\begin{matrix} P \end{matrix}$ 的作用下, 组合梁的轴力为零, 即:

$\begin{matrix} N_{c} (x) + N_{s} (x) + N_{f} (x) = 0 \end{matrix}$ (8)

组合梁的抗力弯矩为:

$\begin{matrix} \begin{matrix} M (x) = M_{c} (x) + M_{s} (x) + N_{c} (x) z_{d} - N_{f} (x) z_{sb} \end{matrix} \end{matrix}$ (9)

外力 $\begin{matrix} P \end{matrix}$ 对简支组合梁产生的弯矩为:

$\begin{matrix} M (x) = \{\begin{matrix} \frac{l_{b}}{l} Px, & x \leq l_{a} \\ \frac{l_{a}}{l} P (l - x), & l_{a} < x \leq l \end{matrix} \end{matrix}$ (10)

根据弹性力学的基本理论, 可知弯矩抗力与外力 $\begin{matrix} P \end{matrix}$ 产生的弯矩平衡, 令 $\begin{matrix} B_{0} = E_{c} I_{c} + E_{s} I_{s}, \end{matrix}$ 由式(4)~(6)可得:

当 $\begin{matrix} 0 \leq x \leq l_{a} \end{matrix}$ 时:

$\begin{matrix} \begin{matrix} B_{0} w ″ (x) + E_{c} A_{c} ε_{c 0} (x) z_{d} - E_{f} A_{f} ε_{f} (x) z_{sb} = \frac{l_{b}}{l} Px \end{matrix} \end{matrix}$ (11)

当 $\begin{matrix} l_{a} < x \leq l \end{matrix}$ 时:

$\begin{matrix} \begin{matrix} B_{0} w ″ (x) + E_{c} A_{c} ε_{c 0} (x) z_{d} - E_{f} A_{f} ε_{f} (x) z_{sb} = \frac{l_{a}}{l} P (l - x) \end{matrix} \end{matrix}$ (12)

2.5 双层结合面组合梁挠曲线方程求解

由式(2)~(7)可得:

$k_{s} [u_{c 0} (x) - u_{s 0} (x) - z_{d} w' (x)] = E_{c} A_{c} u ″_{c 0} (x)$ (13)

$k_{f} [u_{s 0} (x) - u_{f} (x) - z_{sb} w' (x)] = - E_{f} A_{f} u ″_{f} (x)$ (14)

由式(13)可得:

$\begin{matrix} \{\begin{matrix} u'_{s 0} (x) = u'_{c 0} (x) - [\frac{E_{c} A_{c}}{k_{s}} u ‴_{c 0} (x) + z_{d} w ″ (x)] \\ u ″_{s 0} (x) = u ″_{c 0} (x) - [\frac{E_{c} A_{c}}{k_{s}} u_{c 0}^{(4)} (x) + z_{d} w ‴ (x)] \\ u ‴_{s 0} (x) = u ‴_{c 0} (x) - [\frac{E_{c} A_{c}}{k_{s}} u_{c 0}^{(5)} (x) + z_{d} w^{(4)} (x)] \end{matrix} \end{matrix}$ (15)

式中: $\begin{matrix} z_{d} = (z_{cb} + z_{su}) \end{matrix}$

由式(6)(8)可得:

$\begin{matrix} \{\begin{matrix} u'_{f} (x) = - \frac{E_{c} A_{c}}{E_{f} A_{f}} u'_{c 0} (x) - \frac{E_{s} A_{s}}{E_{f} A_{f}} u'_{s 0} (x) \\ u ″_{f} (x) = - \frac{E_{c} A_{c}}{E_{f} A_{f}} u ″_{c 0} (x) - \frac{E_{s} A_{s}}{E_{f} A_{f}} u ″_{s 0} (x) \\ u ‴_{f} (x) = - \frac{E_{c} A_{c}}{E_{f} A_{f}} u ‴_{c 0} (x) - \frac{E_{s} A_{s}}{E_{f} A_{f}} u ‴_{s 0} (x) \end{matrix} \end{matrix}$ (16)

由式(11)(12)可得:

$\begin{matrix} \begin{matrix} w ″ (x) = \\ \{\begin{matrix} \frac{l_{b}}{B_{0} l} Px - k_{Mcs} u'_{c 0} (x) + k_{Mf} u'_{f} (x), 0 \leq x \leq l_{a} \\ \frac{l_{a}}{B_{0} l} P (l - x) - k_{Mcs} u'_{c 0} (x) + k_{Mf} u'_{f} (x), l_{a} \leq x \leq l \end{matrix} \end{matrix} \end{matrix}$ (17)

式中:

$\begin{matrix} k_{Mcs} = \frac{E_{c} A_{c} z_{d}}{B_{0}}, k_{Mf} = \frac{E_{f} A_{f} z_{sb}}{B_{0}} \end{matrix}$

由式(17)可得:

$\begin{matrix} w^{(4)} (x) = - k_{Mcs} u ‴_{c 0} (x) + k_{Mf} u ‴_{f} (x) \end{matrix}$ (18)

由式(13)~(18)可得:

$\begin{matrix} \begin{matrix} a_{1} u_{c 0}^{(5)} (x) + a_{2} u ‴_{c 0} (x) + a_{3} u'_{c 0} (x) = \\ \{\begin{matrix} d_{1} x, & x \leq l_{a} \\ d_{2} (l - x), & l_{a} < x \leq l \end{matrix} \end{matrix} \end{matrix}$ (19)

式中:

$\begin{matrix} a_{1} = \frac{E_{s} A_{s}}{k_{s}} \frac{E_{c} A_{c}}{k_{f}}, \end{matrix}$

$\begin{matrix} \begin{matrix} a_{2} = - \frac{E_{c} A_{c} + E_{s} A_{s}}{k_{f}} - \frac{E_{s} A_{s}}{k_{s}} - \\ \frac{E_{c} A_{c} E_{s} A_{s}}{E_{f} A_{f} k_{s}} - \frac{E_{c} A_{c} E_{s} A_{s} z_{sb}^{2}}{B_{0} k_{s}} - \\ \frac{E_{c} A_{c} E_{s} A_{s} z_{d}^{2}}{B_{0} k_{f}}, \end{matrix} \end{matrix}$

$\begin{matrix} \begin{matrix} a_{3} = 1 + \frac{(E_{c} A_{c} + E_{s} A_{s}) z_{sb}^{2}}{B_{0}} + \\ \frac{E_{c} A_{c} z_{d}^{2}}{B_{0}} + \frac{2 E_{c} A_{c} z_{sb} z_{d}}{B_{0}} + \\ \frac{E_{c} A_{c} E_{s} A_{s} z_{d}^{2}}{B_{0} E_{f} A_{f}} + \frac{E_{c} A_{c} + E_{s} A_{s}}{E_{f} A_{f}}, \end{matrix} \end{matrix}$

$\begin{matrix} d_{1} = (z_{cb} + z_{su} + z_{sb} + \frac{E_{s} A_{s}}{E_{f} A_{f}} z_{d}) \frac{P l_{b}}{a_{3} B_{0} l}, \end{matrix}$

$\begin{matrix} d_{2} = (z_{cb} + z_{su} + z_{sb} + \frac{E_{s} A_{s}}{E_{f} A_{f}} z_{d}) \frac{P l_{a}}{a_{3} B_{0} l} 。 \end{matrix}$

解微分方程(19)可得混凝土顶板截面几何对称轴位置处的轴向应变为:

当 $\begin{matrix} 0 \leq x \leq l_{a} \end{matrix}$ 时:

$\begin{matrix} \begin{matrix} u'_{c} (x) = c_{1} e^{R_{1} x} + c_{2} e^{- R_{1} x} + c_{3} e^{R_{2} x} + c_{4} e^{- R_{2} x} + d_{1} x \end{matrix} \end{matrix}$ (20)

当 $\begin{matrix} l_{a} < x \leq l \end{matrix}$ 时:

$\begin{matrix} \begin{matrix} u'_{c} (x) = c_{5} e^{R_{1} x} + c_{6} e^{- R_{1} x} + c_{7} e^{R_{2} x} + c_{8} e^{- R_{2} x} + d_{2} (l - x) \end{matrix} \end{matrix}$ (21)

式中: $\begin{matrix} c_{1} 、 c_{2} 、 c_{3} 、 c_{4} 、 c_{5} 、 c_{6} 、 c_{7} 、 c_{8} \end{matrix}$ 为待定系数; $\begin{matrix} R_{1} = \sqrt[]{b_{2} - b_{1}}; R_{2} = \sqrt[]{b_{2} + b_{1}}; b_{1} = - a_{2} / (2 a_{1}); b_{2} = \sqrt[]{a_{2}^{2} - 4 a_{1} a_{3}} 。 \end{matrix}$

联立式(15), (16), (20), (21)可得钢梁截面几何对称轴位置处的应变为:

当 $\begin{matrix} 0 \leq x \leq l_{a} \end{matrix}$ 时:

$\begin{matrix} \begin{matrix} u'_{s 0} (x) = (β - R_{1}^{2} α) c_{1} e^{R_{1} x} + \\ (β - R_{1}^{2} α) c_{2} e^{- R_{1} x} + (β - R_{2}^{2} α) c_{3} e^{R_{2} x} + \\ (β - R_{2}^{2} α) c_{4} e^{- R_{2} x} + γ_{1} x \end{matrix} \end{matrix}$ (22)

当 $\begin{matrix} l_{a} < x \leq l \end{matrix}$ 时:

$\begin{matrix} \begin{matrix} u'_{s 0} (x) = (β - R_{1}^{2} α) c_{5} e^{R_{1} x} + (β - R_{1}^{2} α) c_{6} e^{- R_{1} x} + \\ (β - R_{2}^{2} α) c_{7} e^{R_{2} x} + (β - R_{2}^{2} α) c_{8} e^{- R_{2} x} + γ_{2} (l - x) \end{matrix} \end{matrix}$ (23)

式中:

$\begin{matrix} α = E_{c} A_{c} / [k_{s} (1 - \frac{E_{s} A_{s} z_{sb} z_{d}}{B_{0}})], \end{matrix}$

$\begin{matrix} β = \frac{1 + \frac{E_{c} A_{c} z_{d} (z_{d} + z_{sb})}{B_{0}}}{1 - \frac{E_{s} A_{s} z_{sb} z_{d}}{B_{0}}}, \end{matrix}$

$\begin{matrix} γ_{1} = β d_{1} - \frac{l_{b} z_{d}}{B_{0} l} P, \end{matrix}$

$\begin{matrix} γ_{2} = β d_{2} - \frac{l_{a} z_{d}}{B_{0} l} P 。 \end{matrix}$

根据双层结合面简支梁位移连续条件, 轴力连续条件和剪切滑移差的连续条件, 可得如下8个边界条件:

$\begin{matrix} u'_{c 0} (0) = 0, u'_{s 0} (0) = 0, u'_{c 0} (l) = 0, \\ u'_{s 0} (l) = 0, u'_{c 0} (l_{a 左}) = u'_{c 0} (l_{a 右}), \\ u'_{s 0} (l_{a 左}) = u'_{s 0} (l_{a 右}), u ″_{c 0} (l_{a 左}) = u ″_{c 0} (l_{a 右}), u ″_{s 0} (l_{a 左}) = u ″_{s 0} (l_{a 右}) 。 \end{matrix}$

将式(20)~(23)代入上述边界条件, 可得含有 $\begin{matrix} c_{1} ~ c_{8} \end{matrix}$ 八个待定系数的线性方程组, 写成矩阵形式为:

$\begin{matrix} A \cdot C = B \end{matrix}$ (24)

式中:

$\begin{matrix} C = {[\begin{matrix} c_{1} & c_{2} & c_{3} & c_{4} & c_{5} & c_{6} & c_{7} & c_{8} \end{matrix}]}^{T} \end{matrix}$

$\begin{matrix} \begin{matrix} A = [\begin{matrix} 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & e^{R_{1} l} & e^{- R_{1} l} & e^{R_{2} l} & e^{- R_{2} l} \\ α_{R 1} & α_{R 1} & α_{R 2} & α_{R 2} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & α_{R 1} e^{R_{1} l} & α_{R 1} e^{- R_{1} l} & α_{R 2} e^{R_{2} l} & α_{R 2} e^{- R_{2} l} \\ e^{R_{1} l_{a}} & e^{- R_{1} l_{a}} & e^{R_{2} l_{a}} & e^{- R_{2} l_{a}} & - e^{R_{1} l_{a}} & - e^{- R_{1} l_{a}} & - e^{R_{2} l_{a}} & - e^{- R_{2} l_{a}} \\ α_{R 1} e^{R_{1} l_{a}} & α_{R 1} e^{- R_{1} l_{a}} & α_{R 2} e^{R_{2} l_{a}} & α_{R 2} e^{- R_{2} l_{a}} & - α_{R 1} e^{R_{1} l_{a}} & - α_{R 1} e^{- R_{1} l_{a}} & - α_{R 2} e^{R_{2} l_{a}} & - α_{R 2} e^{- R_{2} l_{a}} \\ R_{1} e^{R_{1} l_{a}} & - R_{1} e^{- R_{1} l_{a}} & R_{2} e^{R_{2} l_{a}} & - R_{2} e^{- R_{2} l_{a}} & - R_{1} e^{R_{1} l_{a}} & R_{1} e^{- R_{1} l_{a}} & - R_{2} e^{R_{2} l_{a}} & R_{2} e^{- R_{2} l_{a}} \\ α_{R 1} R_{1} e^{R_{1} l_{a}} & - α_{R 1} R_{1} e^{- R_{1} l_{a}} & α_{R 2} R_{2} e^{R_{2} l_{a}} & - α_{R 2} R_{2} e^{- R_{2} l_{a}} & - α_{R 1} R_{1} e^{R_{1} l_{a}} & α_{R 1} R_{1} e^{- R_{1} l_{a}} & - α_{R 2} R_{2} e^{R_{2} l_{a}} & α_{R 2} R_{2} e^{- R_{2} l_{a}} \end{matrix}] \\ B = [\begin{matrix} 0 & 0 & 0 & 0 & - d_{1} l_{a} + d_{2} (l - l_{a}) & - γ_{1} l_{a} + γ_{2} (l - l_{a}) & - d_{1} - d_{2} & - γ_{1} + γ_{2} \end{matrix}] \end{matrix} \end{matrix}$

式中: $\begin{matrix} α_{R 1} = (β - R_{1}^{2} α), α_{R 2} = (β - R_{2}^{2} α) 。 \end{matrix}$

解方程(24)可得:

$\begin{matrix} C = A^{- 1} B \end{matrix}$ (25)

由公式(17)(20)(21)(22)(23)(25)可以得到双层结合面组合梁的挠曲线方程表达式如式(26)所示:

$\begin{matrix} w (x) = \{\begin{matrix} c_{α} \frac{1}{R_{1}^{2}} c_{1} e^{R_{1} x} + c_{α} \frac{1}{R_{1}^{2}} c_{2} e^{- R_{1} x} + c_{β} \frac{1}{R_{2}^{2}} c_{3} e^{R_{2} x} + c_{β} \frac{1}{R_{2}^{2}} c_{4} e^{- R_{2} x} + \frac{1}{6} c_{γ 1} x^{3} + c_{9} x + c_{10}, & 0 \leq x \leq l_{a} \\ c_{α} \frac{1}{R_{1}^{2}} c_{5} e^{R_{1} x} + c_{α} \frac{1}{R_{1}^{2}} c_{6} e^{- R_{1} x} + c_{β} \frac{1}{R_{2}^{2}} c_{7} e^{R_{2} x} + c_{β} \frac{1}{R_{2}^{2}} c_{8} e^{- R_{2} x} + c_{γ 2} (\frac{l}{2} x^{2} - \frac{1}{6} x^{3}) + c_{11} x + c_{12}, & l_{a} < x \leq l \end{matrix} (26) \end{matrix}$

式中: c₉ , c₁₀ , c₁₁ , c₁₂ 为待定系数, 根据集中荷载作用下简支梁的位移边界条件w(0)=0, w(l)=0, w'(la_左)=w'(la_右), w(la_左)=w(la_右)可得如下方程:

$\begin{matrix} A' C' = B' \end{matrix}$ (27)

式中:

$\begin{matrix} \begin{matrix} A' = [\begin{matrix} 0 & 0 & 1 & 0 \\ 0 & l & 0 & 1 \\ l_{a} & - l_{a} & 1 & - 1 \\ 1 & - 1 & 0 & 0 \end{matrix}], \\ C' = [c_{9} c_{10} c_{11} c_{12}]^{T}, \\ B' = [B_{1} B_{2} B_{3} B_{4}]^{T}, \\ B_{1} = - \frac{c_{α} c_{1}}{R_{1}^{2}} - \frac{c_{α} c_{2}}{R_{1}^{2}} - \frac{c_{β} c_{3}}{R_{2}^{2}} - \frac{c_{β} c_{4}}{R_{2}^{2}}, \\ B_{2} = - \frac{c_{α} c_{5}}{R_{1}^{2}} e^{R_{1} l} - \frac{c_{α} c_{6}}{R_{1}^{2}} e^{- R_{1} l} - \\ \frac{c_{β} c_{7}}{R_{2}^{2}} e^{R_{2} l} - \frac{c_{β} c_{8}}{R_{2}^{2}} e^{- R_{2} l} - \frac{c_{χ 2} l^{3}}{3}, \\ B_{3} = \frac{c_{α} (c_{5} - c_{1})}{R_{1}^{2}} e^{R_{1} l_{a}} + \frac{c_{α} (c_{6} - c_{2})}{R_{1}^{2}} e^{- R_{1} l_{a}} + \\ \frac{c_{β} (c_{7} - c_{3})}{R_{2}^{2}} e^{R_{2} l_{a}} + \frac{c_{β} (c_{8} - c_{4})}{R_{2}^{2}} e^{- R_{2} l_{a}} + \\ c_{γ_{2}} (\frac{l \cdot l_{a}}{2} - \frac{l_{a}^{3}}{6}) - c_{γ_{1}} \frac{l_{a}^{3}}{6} \\ B_{4} = \frac{c_{α} (c_{5} - c_{1})}{R_{1}} e^{R_{1} l_{a}} + \frac{c_{α} (c_{6} - c_{2})}{R_{1}} e^{- R_{1} l_{a}} + \\ \frac{c_{β} (c_{7} - c_{3})}{R_{2}} e^{R_{2} l_{a}} + \frac{c_{β} (c_{8} - c_{4})}{R_{2}} e^{- R_{2} l_{a}} + \\ c_{γ_{2}} (l \cdot l_{a} - \frac{l_{a}^{3}}{2}) - c_{γ_{1}} \frac{l_{a}^{2}}{2} 。 \end{matrix} \end{matrix}$

$\begin{matrix} \begin{matrix} c_{α} = \frac{E_{c} A_{c} E_{s} A_{s} z_{sb}}{k_{s} (B_{0} - E_{s} A_{s} z_{sb} z_{d})} R_{1}^{2} - \\ \frac{E_{c} A_{c} (z_{d} + z_{sb}) + E_{s} A_{s} z_{sb}}{(B_{0} - E_{s} A_{s} z_{sb} z_{d})}, \end{matrix} \end{matrix}$

$\begin{matrix} \begin{matrix} c_{β} = \frac{E_{c} A_{c} E_{s} A_{s} z_{sb}}{k_{s} (B_{0} - E_{s} A_{s} z_{sb} z_{d})} R_{2}^{2} - \\ \frac{E_{c} A_{c} (z_{d} + z_{sb}) + E_{s} A_{s} z_{sb}}{(B_{0} - E_{s} A_{s} z_{sb} z_{d})}, \end{matrix} \end{matrix}$

$\begin{matrix} \begin{matrix} c_{γ_{1}} = \frac{l_{b} P}{l (B_{0} - E_{s} A_{s} z_{sb} z_{d})} - \\ \frac{E_{c} A_{c} (z_{d} + z_{sb}) + E_{s} A_{s} z_{sb}}{(B_{0} - E_{s} A_{s} z_{sb} z_{d})} d_{1}, \\ c_{γ_{2}} = \frac{l_{a} P}{l (B_{0} - E_{s} A_{s} z_{sb} z_{d})} - \\ \frac{E_{c} A_{c} (z_{d} + z_{sb}) + E_{s} A_{s} z_{sb}}{(B_{0} - E_{s} A_{s} z_{sb} z_{d})} d_{2} 。 \end{matrix} \end{matrix}$

由式(27)可解得 $\begin{matrix} c_{9} 、 c_{10} 、 c_{11} 、 c_{12} \end{matrix}$ 四个待定系数系数:

$\begin{matrix} C' = A'^{- 1} B' \end{matrix}$ (28)

3 算例及分析

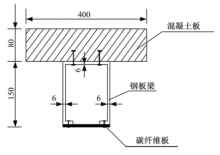
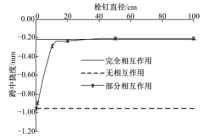
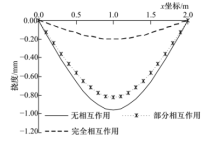
为验证本文推导公式的正确性, 以横断面如图5所示的跨度为2 m, 10 kN的集中力作用于跨中截面的双层结合面碳纤维-钢-混凝土简支组合梁为例, 计算了当栓钉直径由小到大(即交界面的剪切刚度由小到大)逐渐增加过程中的跨中挠度, 将本文给出的解析解与按简单梁理论计算的结果进行了比较, 对比结果如图6, 图7所示.从图6中可以看出:在交界面剪切刚度逐渐增加过程中, 跨中挠度从无相互作用的最大值开始逐渐接近完全相互作用对应的简单梁理论计算结果, 符合预期结果.图7给出了跨中集中力作用下, 当组合梁在交界面处无相互作用, 部分相互作用, 完全相互作用时的挠曲线, 部分相互作用对应的挠曲线位于无相互作用和完全相互作用对应的挠曲线之间, 进一步验证了本文给出的计算方法的准确性.从图6和图7给出的结果中可以肯定本文推导的基本理论是合理的, 可信的.

	Figure Option View Download New Window
	图5 组合梁一般构造(mm)Fig.5 Composite beam general construction unit(mm)

	Figure Option View Download New Window
	图6 跨中挠度与栓钉直径的关系Fig.6 Span deflection relationship with stud diameter

	Figure Option View Download New Window
	图7 挠度曲线Fig.7 Deflection curve

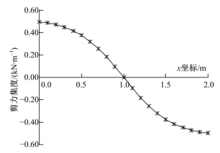
碳纤维-钢-混凝土组合梁三种材料能够共同协调受力的关键是在交界面设置了一定数量的剪力连接件(即本文对应的栓钉), 但目前栓钉直径和间距的设置主要依靠经验算法, 利用本文的理论可以精确计算出交界面处的剪力集度, 根据公式(7)和文献^[6]给出的剪切刚度计算方法, 可以方便地计算出栓钉的布置数量, 为实际工程设计栓钉提供了准确的理论依据.剪力集度沿梁长的分布曲线如图8所示, 从图8中可以看出, 在跨中集中力作用下, 支点附近的剪力集度较大, 栓钉沿梁长的间距应与剪力集度的分布规律一致, 或者保守地按支点处的剪力集度等间距布置栓钉.

	Figure Option View Download New Window
	图8 交界面剪力集度曲线Fig.8 Interface shear stress curve

4 结论

(1)基于弹性力学理论推导了具有双层结合面的碳纤维-钢-混凝土组合梁在集中荷载作用下的解析解, 建立了在竖向集中荷载作用下考虑交界面剪切滑移的具有双层结合面的组合梁应变和位移表达式.

(2)通过算例验证了该解析解的正确性, 解决了在考虑剪切滑移时的双层结合面组合梁无解析计算的难题, 为该组合梁的工程应用奠定了理论基础.

(3)通过具体算例说明了在设计组合梁剪力连接件时, 应沿梁长变间距布置.

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	聂建国, 余志斌. 钢-混凝土组合梁在我国的研究及应用[J]. 土木工程学报, 1999, 32(2): 3-8. Nie Jian-guo, Yu Zhi-bin. Research and practice of composite steel-concrete beams in China[J]. China Civil Engineering Journal, 1999, 32(2): 3-8. [本文引用:1]
[2]	刘寒冰, 马辉, 刘天明, 等. 竖向集中荷载作用下钢-混凝土组合梁的解析解[J]. 中国公路学报, 2010, 23(4): 39-44. Liu Han-bing, Ma Hui, Liu Tian-ming, et al. Analytical solution of a steel-concrete composite beam under vertical loads[J]. China Journal of Highway and Transport , 2010, 23(4): 39-44. [本文引用:1]
[3]	余志武, 蒋丽忠, 李佳. 集中荷载作用下钢-混凝土组合梁截面滑移及变形[J]. 土木工程学报, 2003, 36(8): 1-6. Yu Zhi-wu, Jiang Li-zhong, Li Jia. The interface slip and deformation of steel-concrete composite beams under concentrated loads[J]. China Civil Engineering Journal, 2003, 36(8): 1-6. [本文引用:1]
[4]	邵晓辉, 段树金. 均布荷载作用下双面组合梁的滑移效应分析[J]. 石家庄铁道学院学报: 自然科学版, 2007, 20(4): 40-44. Shao Xiao-hui, Duan Shu-jin. Analysis of interface slip Effect of double steel-concrete composite beam under uniform load[J]. Journal of Shijiazhuang Railway Institute (NaturaL Science), 2007, 20(4): 40-44. [本文引用:1]
[5]	劳埃杨. 钢-混凝土组合结构设计[M]. 张陪信译. 上海: 同济大学出版社, 1991. [本文引用:2]
[6]	刘寒冰, 刘文会, 张云龙. 集中荷载作用下组合梁剪切滑移计算分析[J]. 应用数学和力学, 2005, 26(6): 677-682. Liu Han-bing, Liu Wen-hui, Zhang Yun-long. Cal- culation analysis of shearing slip for steel-concrete composite beam under concentrated load[J]. Applied Mathematics and Mechanics, 2005, 26(6): 677-682. [本文引用:2]
[7]	苗林, 陈德伟. 考虑层间滑移效应的组合梁解析计算[J]. 同济大学学报: 自然科学版, 2011, 39(8): 1113-1119. Miao Lin, Chen De-wei. Closed-form solution of composite beam considering interfacial slip effects[J]. Journal of Tongji University(Natural Science), 2011, 39(8): 1113-1119. [本文引用:1]
[8]	谢峻, 余天庆. 部分剪力连接钢-混凝土组合梁的截面抗弯分析[J]. 南京理工大学学报, 2000, 24(5): 453-456. Xie Jun, Yu Tian-qing. Analysis of bending capacity of steel-concrete composite beams with partial shear connection[J]. Journal of Nanjing University of Science and Technology, 2000, 24(5): 453-456. [本文引用:1]
[9]	刘航, 李晨光, 聂建国. 体外预应力钢与混凝土组合梁试验研究[J]. 建筑技术开发, 2002, 29(11): 1-2. Liu Hang, Li Chen-guang, Nie Jian-guo. Experimental research on prestressed steel & concrete composite beam[J]. Building Technique Development, 2002, 29(11): 1-2. [本文引用:1]

1999

0.0

. 1999, 32(2):3-8 DOI:doi:10.3321/j.issn:1000-131X.1999.02.001

Research and practice of composite steel-concrete beams in China

钢-混凝土组合梁在我国的研究及应用

Nie Jian-guo , Yu Zhi-bin.

聂建国, 余志斌

近年来,钢-混凝土组合梁结构在我国发展很快,在建筑和桥梁结构等领域已经得到越来越多的应用,取得了显著的技术经济效益和社会效益.本文较为系统地阐述组合梁在我国的研究和应用情况,并指出了有关钢-混凝土组合梁方面值得进一步研究的问题.

... 由于该种结构具有质量轻,承载力大,跨越能力强,施工方便等优点^[1,2,3,4,5],对有高度及跨度要求的建筑采用组合梁比较合适 ...

2010

0.0

. 2010, 23(4):39-44

Analytical solution of a steel-concrete composite beam under vertical loads

竖向集中荷载作用下钢-混凝土组合梁的解析解

Liu Han-bing , Ma Hui , Liu Tian-ming

刘寒冰, 马辉, 刘天明

In order to accurately analyze the flexural behavior of steel-concrete composite beam, based on contact theory and basic idea of elastic mechanics and considering the shear-slip effect, differential equation of the structure under vertical load was deduced and analytical solution was given. The strain and displacement conditions of composite beam under vertical load were calculated by the analytical solution. Shear-slip strain difference of interface of steel beam and concrete top slab was also analyzed. The results calculated by this method were compared with test result. Result shows that test value has a good agreement with calculated value obtained from a simple beam experiment, and the deflection error is less than 2%. It is concluded that this equation is rational, believable and practical. The method can be used as a simple and convenient analytical method for construction design.

为了准确分析钢-混凝土组合梁的抗弯性能,基于接触理论和弹性力学基本思想推导了钢-混凝土组合梁在竖向荷载作用下考虑剪切滑移效应的微分方程,给出了解析解。计算了竖向集中力作用下组合梁的各部分应变和位移状态,分析了钢梁和混凝土顶板交界面处的剪切滑移应变差,并与试验结果进行了对比。结果表明:计算值与试验值有较好的一致性,挠度相对误差不超过2%;该计算公式是合理的、可信的,为工程设计提供了一种简便的计算方法,具有较强的实用价值。

... 由于该种结构具有质量轻,承载力大,跨越能力强,施工方便等优点^[1,2,3,4,5],对有高度及跨度要求的建筑采用组合梁比较合适 ...

2003

0.0

... 由于该种结构具有质量轻,承载力大,跨越能力强,施工方便等优点^[1,2,3,4,5],对有高度及跨度要求的建筑采用组合梁比较合适 ...

2007

0.0

. 2007, 20(4):40-44 DOI:doi:10.3969/j.issn.2095-0373.2007.04.010

Analysis of interface slip Effect of double steel-concrete composite beam under uniform load

均布荷载作用下双面组合梁的滑移效应分析

Shao Xiao-hui , Duan Shu-jin.

邵晓辉, 段树金

利用基本力学方法对钢-混凝土双面组合梁在均布荷载作用下的滑移效应进行分析,推导得到了负弯矩区上、下交界面滑移沿梁长方向的表达式,并通过算例比较了双面组合梁与传统单面连续组合梁的滑移特点.计算表明,与传统单面连续组合梁相比,钢-混凝土双面组合连续梁不仅在负弯矩区提高了截面承载力,也使截面刚度得到了提高.

... 由于该种结构具有质量轻,承载力大,跨越能力强,施工方便等优点^[1,2,3,4,5],对有高度及跨度要求的建筑采用组合梁比较合适 ...

1991

0.0

... 由于该种结构具有质量轻,承载力大,跨越能力强,施工方便等优点^[1,2,3,4,5],对有高度及跨度要求的建筑采用组合梁比较合适 ...

... 由文献^[5]可知: ...

2005

0.0

. 2005, 26(6):677-682 DOI:doi:10.3321/j.issn:1000-0887.2005.06.008

Cal- culation analysis of shearing slip for steel-concrete composite beam under concentrated load

集中荷载作用下组合梁剪切滑移计算分析

Liu Han-bing , Liu Wen-hui , Zhang Yun-long.

刘寒冰, 刘文会, 张云龙

The strain's difference of steel and concrete under vertical concentrated load was analyzed on the basis of elastic theory,and was compared with ideal solution of steel and concrete under vertical uniform load.The results indicate that the computing formula concluded from the paper is believable.The practical structure usually bears concentrated load,so it can be used in the practical engineering.

基于弹性理论，对钢-混凝土组合梁在竖向集中荷载作用下的剪切滑移应变差进行了理论分析，并与均布荷载作用下公认的理论解进行了计算对比．结果表明,所推导的在集中荷载作用下，钢-混凝土组合梁的剪切滑移应变差的计算公式是可信的．因为实际工程多为集中荷载作用，所以用该计算公式可以很方便的解决工程实际问题．

... 近些年组合梁应用于公路及城市桥梁工程中比较普遍,因此,有关组合梁理论及试验研究也成为土木工程领域的研究热点之一^[6,7,8,9] ...

... 碳纤维-钢-混凝土组合梁三种材料能够共同协调受力的关键是在交界面设置了一定数量的剪力连接件(即本文对应的栓钉),但目前栓钉直径和间距的设置主要依靠经验算法,利用本文的理论可以精确计算出交界面处的剪力集度,根据公式(7)和文献^[6]给出的剪切刚度计算方法,可以方便地计算出栓钉的布置数量,为实际工程设计栓钉提供了准确的理论依据 ...

2011

0.0

. 2011, 39(8):1113-1119 DOI:doi:10.3969/j.issn.0253-374x.2011.08.003

Closed-form solution of composite beam considering interfacial slip effects

考虑层间滑移效应的组合梁解析计算

Miao Lin , Chen De-wei.

苗林, 陈德伟

Based on Goodman model,which is used for simulating the contact surface between beams,this paper presents an analysis of the relationship interfacial slip of composite beam,internal force,deflection and load in elastic state.For the simply supported and cantilever beams subjected to variety of loads,the impacts on deformation due to the interfacial slip are considered through the “additional slip bending moment”.This theoretical formula can describe the law of slip,deflection and sectional stress distribution.The closed form solutions are then validated by means of finite element analysis.All the theoretical formula in the paper which reflects the structural mechanism can simplify calculation of interfacial slip effects of composite beam.

将双层组合梁的接触面模拟成Goodman弹性夹层,用Goodman弹性夹层法分析双层组合梁在弹性工作阶段的滑移、内力及挠度与荷载之间的关系.分别针对简支梁、悬臂梁在多种荷载作用下,根据边界条件计算出梁在该荷载约束条件下的内力、滑移和挠度分布规律,通过“滑移附加弯矩”引入层间相对滑移对组合梁的影响.该理论公式既能描述组合梁的界面滑移规律,又可以计算界面滑移对组合梁变形挠度及截面应力分布的影响.利用通用有限元软件对组合梁的界面滑移与变形进行了有限元分析,验证了解析计算结果.所得的理论计算公式物理意义明确,简化了组合梁结构截面应力分布和变形挠度的计算.

... 近些年组合梁应用于公路及城市桥梁工程中比较普遍,因此,有关组合梁理论及试验研究也成为土木工程领域的研究热点之一^[6,7,8,9] ...

2000

0.0

... 近些年组合梁应用于公路及城市桥梁工程中比较普遍,因此,有关组合梁理论及试验研究也成为土木工程领域的研究热点之一^[6,7,8,9] ...

2002

0.0

. 2002, 29(11):1-2

Experimental research on prestressed steel #cod#x00026; concrete composite beam

体外预应力钢与混凝土组合梁试验研究

Liu Hang , Li Chen-guang , Nie Jian-guo.

刘航, 李晨光, 聂建国

进行了5根简支体外预应力钢与混凝土组合梁在竖向荷载下的试验研究.对比分析了普通钢与混凝土组合梁、预应力钢与混凝土组合梁和预应力加固钢与混凝土组合梁的受力性能与破坏形态.

... 近些年组合梁应用于公路及城市桥梁工程中比较普遍,因此,有关组合梁理论及试验研究也成为土木工程领域的研究热点之一^[6,7,8,9] ...