排桩支护结构内力与变形三维有限元数值分析

引用本文

胡玉明, 黄音, 古海东. 排桩支护结构内力与变形三维有限元数值分析.吉林大学学报:工学版, 2016, 46(2): 445-450
HU Yu-ming, HUANG Yin, GU Hai-dong. Three-dimensional finite element analysis of internal forces and displacement of scattered row piles. Journal of Jilin University Engineering and Technology Edition, 2016, 46(2): 445-450 复制到剪切板

Permissions

排桩支护结构内力与变形三维有限元数值分析

胡玉明^1,², 黄音³, 古海东⁴

1.四川大学水利水电学院,成都 610065

2.四川盛唐建设工程有限公司,成都 610042

3.重庆大学土木工程学院,重庆 400045

4.浙江交通规划设计院,杭州 310006

通讯作者:黄音(1971-),男,副教授,博士.研究方向:预应力混凝土结构,结构检测与加固.E-mail:1450481918@qq.com

作者简介:胡玉明(1971-),男,高级工程师,博士研究生.研究方向:土木工程及水电建设.E-mail:huym8088@sina.com

基金:国家自然科学基金项目(51078370); 重庆市科委攻关项目(2011AC4067)

摘要

针对离心模型试验建立了三维有限元数值模型,通过与试验的比较验证了模型的可靠性,并与规范法中的 m法进行了比较分析.结合一个悬臂排桩支护结构实例分析了桩身截面尺寸,桩间距和土体强度参数对桩身内力和变形的影响规律.研究表明:采用 m法进行排桩支护结构设计偏于保守,与 m法相比三维有限元法计算结果与离心机试验结果更为接近;桩身弯矩和桩顶水平位移随桩间净距的增加和桩身截面宽度的减小近似呈线性增加,随着土体黏聚力和内摩擦角的增加近似呈指数形式增加.

关键词: 排桩支护; 离心模型试验; 三维有限元法

中图分类号:TU47 文献标志码:A 文章编号:1671-5497(2016)02-0445-06

Three-dimensional finite element analysis of internal forces and displacement of scattered row piles

HU Yu-ming^1,², HUANG Yin³, GU Hai-dong⁴

1.College of Water Resource & Hydropower, Sichuan University, Chengdu 610065,China

2.Sichuan Suntang Construction Engineering Co., Ltd., Chengdu 610042 ,China

3.School of Civil Engineering, Chongqing University, Chongqing 400045,China

4.Zhejiang Institute of Communications Planning,Design & Research,Hangzhou 310006,China

Abstract

A three-dimensional Finite Element Model (FEM) of centrifuge was established first, and the reliability of the model was validated by centrifuge test. Then this method was compared with the current specified m-method. A case study of cantilever row piles was carried out to analyze the impact factors to the internal force and head horizontal displacement of the pile. These impact factors include the cross-section area of the pile, the pile spacing and soil strength. Results show that the design of row pile retaining structure by the m-method is conservative. The three-dimensional FEM method is more consistent with the centrifuge testing results than the m-method. The bending moment and the horizontal displacement of the pile linearly increase as the pile spacing increases and the pile width decreases. They nearly exponentially increase with the cohesion and internal friction angle of the soil.

Keyword: row pile protection; centrifuge; three-dimensional FEM

Show Figures

0 引言

深基坑支护结构设计一直以来都是岩土工程领域里的一个热点和难点问题, 对于深基坑排桩支护结构, 常用的设计方法有等值梁法和弹性地基梁法, 目前, 在工程设计中, 多采用国家行业标准(JGJ120-2012)^[1]中的弹性支点法(m法), 同济大学的杨敏在文献[2]中给出了弹性支点法(m法)的有限元实现过程, 并编制和开发了相应的计算软件----同济启明星深基坑支挡结构分析计算软件, 并采用该软件对维护结构变形和变形性状影响因素进行了分析和讨论^[3].规范法^[1]中的计算模型对单根支护桩上的主动土压力计算宽度取为排桩间距.只有当桩间土体的土压力完全通过土拱效应传递给排桩时, 排桩计算宽度取桩间距才较为合理, 然而, 实际中土拱效应能否存在以及土拱效应能传递多少土压力给排桩还有待进一步的研究^{[4, 5, 6, 7]}.因此, 对深基坑排桩支护结构进行考虑空间效应的三维模型试验和三维有限元数值分析是十分必要的.古海东等^[8]通过一组离心机模型试验分析了深基坑排桩支护结构的桩身内力分布情况以及支护结构破坏模式.

本文结合文献^[8]中的离心机模型试验建立了三维有限元模型, 通过与离心模型试验的比较, 验证了三维有限元模型的合理性, 并探讨了规范法计算排桩内力的适宜性.结合一个排桩支护结构实例分析了桩身截面尺寸, 桩间距以及土体强度参数对桩身内力和变形的影响规律.

1 三维有限元数值分析

1.1 三维有限元方法可靠性验证

古海东等^[8]通过一组离心机模型试验分析了深基坑排桩支护结构的桩身内力分布情况.试验得到的不同离心加速度下的支护桩桩身弯矩如图1所示.

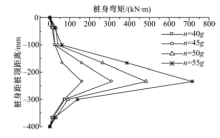	Figure Option View Download New Window
	图1 不同离心加速度(g)下的桩身弯矩分布图Fig.1 Distribution of the bending moment pile under different centrifugal acceleration

本文针对文献[8]中的离心机模型试验, 建立了三维有限元数值模型, 为了建模方便, 有限元模型中采用实心混凝土方形截面桩, 设方形截面桩的宽度为b, 根据等效抗弯刚度原则, 不同离心加速度下对应的有限元模型桩宽度为:

$\begin{matrix} b = n \times \sqrt[4]{\frac{12 π \times E_{L} \times (D^{4} - d^{4})}{64 \times E_{c}}} \end{matrix}$ (1)

式中: $\begin{matrix} n \end{matrix}$ 为离心加速度; $\begin{matrix} E_{L} \end{matrix}$ 和 $\begin{matrix} E_{c} \end{matrix}$ 分别为空心铝管桩和实心混凝土桩的弹性模量; $\begin{matrix} D 和 d \end{matrix}$ 分别为离心试验模型桩的外径和内径.

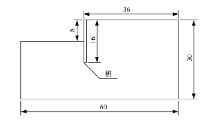
为了减少计算时间, 有限元模型采用对称结构, 选取相邻两桩中心距间的土体作为研究对象, 基坑土体尺寸按离心机试验原型尺寸乘以相应的离心加速度来确定, 有限元模型简图如图2所示.有限元模型中桩体采用线弹性本构模型, 土体采用摩尔-库伦本构模型, 同时为了考虑桩与土体间的相互作用, 在ABAQUS中桩和土体采用摩擦接触, 切线方向接触属性为罚函(Penalty), 法线方向为硬接触.为了和离心机模型试验保持一致, 有限元分析中通过调用ABAQUS中的MODEL CHANGE, REMOVE命令模拟土体开挖.

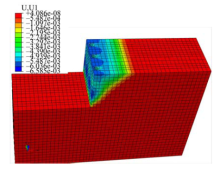
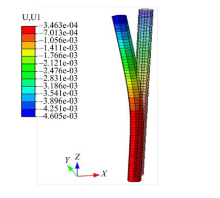
	Figure Option View Download New Window
	图2 有限元网格划分Fig.2 FEM model

图3和图4分别为对应离心加速度为50g(g表示重力加速度)时的有限元计算结果中的基坑水平位移云图和排桩水平位移云图.

	Figure Option View Download New Window
	图3 基坑开挖后支护结构水平位移云图Fig.3 Horizontal displacement contour of retaining structure after excavation

	Figure Option View Download New Window
	图4 基坑开挖后支护排桩的水平位移Fig.4 Horizontal displacement contour of supporting piles after excavation

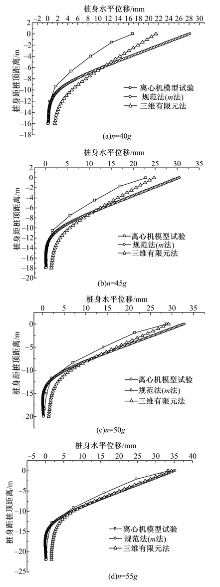
为了验证三维有限元模型计算结果的合理性, 将离心模型试验得出的桩身弯矩和桩身水平位移以及建筑基坑支护技术规程(JGJ120-2012)^[1]中的m法计算结果进行了对比分析, 桩身弯矩和桩身水平位移分布图如图5和图6所示.其中m法中m的取值采用规程^[1]中的推荐经验公式:

$\begin{matrix} m = \frac{1}{Δ} (0.2 φ^{2} - φ + c) \end{matrix}$ (2)

式中: $\begin{matrix} c \end{matrix}$ 和 $\begin{matrix} φ \end{matrix}$ 分别为土体固结不排水的黏聚力和内摩擦角; $\begin{matrix} Δ \end{matrix}$ 取10 mm.将 $\begin{matrix} c \end{matrix}$ 和 $\begin{matrix} φ \end{matrix}$ 的值代入式(2)得出本文所用基坑模型的 $\begin{matrix} m \end{matrix}$ 值为22.48 MN/m⁴.

由图5和图6可知:采用三维有限元法计算得到的桩身弯矩和水平位移分布形态与离心机模型试验以及 $\begin{matrix} m \end{matrix}$ 法计算结果基本一致.与 $\begin{matrix} m \end{matrix}$ 法计算结果相比, 三维有限元法计算结果与离心机试验结果更为接近, 随着离心加速度的不断增加, 三维有限元法计算结果与规范法及离心机试验结果越来越接近.其主要原因是, 离心加速度越大时支护桩间土体不均匀位移越大, 土拱效应越明显, 排桩承担的土压力荷载也越大.

	Figure Option View Download New Window
	图5 不同计算方法得出的桩身弯矩分布曲线Fig.5 Bending moment distribution of pile under different methods

	Figure Option View Download New Window
	图6 不同计算方法得出的桩身水平位移分布曲线Fig.6 Horizontal displacement distribution of pile under different methods

由以上分析结果可知, 本文采用的三维有限元分析模型分析深基坑排桩支护结构的桩身内力的结果是合理, 可靠的.

1.2 桩身内力影响因素分析

1.2.1 桩间净距的影响

分别取桩身截面宽度 $\begin{matrix} b \end{matrix}$ 为0.5, 1, 1.5和2 m保持不变, 依次取排桩净间距 $\begin{matrix} s \end{matrix}$ 为1, 3, 5和7 m研究排桩净间距对桩身最大弯矩和桩顶水平位移的影响, 基坑开挖深度为8 m, 桩长为16 m, 土层参数和上文保持一致, 模型截面尺寸如图7所示.

	Figure Option View Download New Window
	图7 基坑模型简图(单位:m)Fig.7 Foundation model diagram(m)

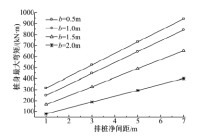
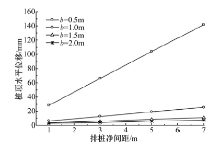
图8和图9分别为不同桩间距下的桩身最大弯矩和桩顶水平位移图.由图可知:桩身最大弯矩和桩顶水平位移随排桩净间距的增大近似呈线性增长, 当桩身截面宽度为0.5 m时, 桩顶水平位移随排桩净间距线性增长的速率最大.

	Figure Option View Download New Window
	图8 桩间净距对桩身最大弯矩的影响Fig.8 Influence of net spacing of pile on its maximum bending moment

	Figure Option View Download New Window
	图9 桩间净距对桩顶水平位移的影响Fig.9 Influence of net spacing of pile on its top horizontal displacement

1.2.2 桩身截面宽度的影响

分别取排桩净间距 $\begin{matrix} s \end{matrix}$ 为1, 3, 5和7 m保持不变, 依次取桩身截面宽度 $\begin{matrix} b \end{matrix}$ 为0.5, 1, 1.5和2 m研究桩身截面宽度对桩身最大弯矩和桩顶水平位移的影响, 图10和图11分别为不同桩截面宽度下的桩身最大弯矩和桩顶水平位移图.

	Figure Option View Download New Window
	图10 桩身截面宽度对桩身最大弯矩的影响Fig.10 Influence of section width of pile on its maximum bending moment

	Figure Option View Download New Window
	图11 桩身截面宽度对桩顶水平位移的影响Fig.11 Influence of section width of pile on its top horizontal displacement

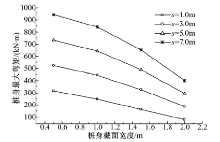
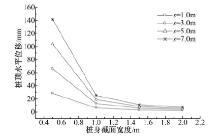
由图10和图11可知:桩身最大弯矩随桩身截面宽度的增大近似呈线性减小, 桩顶水平位移随着桩身截面宽度的增大近似呈指数形式衰减.

1.2.3 土体强度参数的影响

(1)土体内摩擦角的影响

取桩身截面宽度b=1 m, 桩间净距s=4 m, 土体黏聚力c=23 kPa保持不变, 依次取土体内摩擦角为5° , 10° , 15° , 20° , 25° , 30° 和35° , 通过三维有限元计算研究土体内摩擦角对桩身最大弯矩和桩顶水平位移的影响, 计算结果如图12和图13所示.由图可知:当土体黏聚力一定时, 桩身最大弯矩和桩顶水平位移随着土体内摩擦角的增大呈指数形式衰减.

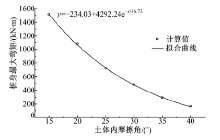	Figure Option View Download New Window
	图12 土体内摩擦角对桩身最大弯矩的影响Fig.12 Influence of internal friction angel of soil on maximum bending moment of pile

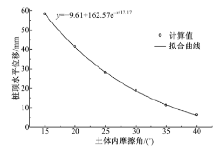	Figure Option View Download New Window
	图13 土体内摩擦角对桩顶水平位移的影响Fig.13 Influence of internal friction angel of soil on horizontal displacement of top pile

(2)土体黏聚力的影响

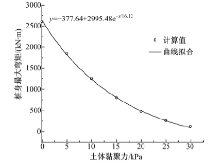
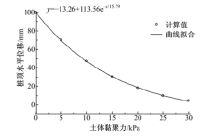
取桩身截面宽度b=1 m, 桩间净距s=4 m, 土体内摩擦角φ =34° 保持不变, 依次取土体黏聚力为0, 5, 10, 15, 20, 25和30 kPa, 通过三维有限元计算研究土体黏聚力对桩身最大弯矩和桩顶水平位移的影响, 计算结果如图14和图15所示.

	Figure Option View Download New Window
	图14 土体黏聚力对桩身最大弯矩的影响Fig.14 Influence of cohesion of soil on maximum bending moment of pile

	Figure Option View Download New Window
	图15 土体黏聚力对桩顶水平位移的影响Fig.15 Influence of cohesion of soil on horizontal displacement of top pile

由图可知:当土体内摩擦角一定时, 桩身最大弯矩和桩顶水平位移随着土体黏聚力的增大呈指数形式衰减.

2 结论

(1)采用三维有限元计算得到的桩身内力和变形与离心机试验值基本吻合, 说明采用三维有限元法计算排桩支护基坑桩身内力与变形是合理可行的.

(2)规范法(m法)计算得到的桩身弯矩和桩身水平位移均比离心机试验值大, m法得到的桩身最大弯矩是离心机试验值的1.23~1.88倍, 采用规范法(m法)进行排桩支护设计偏保守.

(3)桩身最大弯矩和桩顶水平位移随着桩间净距以及桩身截面宽度的增大近似呈线性增加, 随着土体黏聚力和土体内摩擦角的增加近似呈指数形式增加.

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	JGJ120-2012. 建筑基坑支护技术规程[S]. [本文引用:4]
[2]	杨敏, 王瑞祥, 冯又全. 基坑挡墙结构的设计: I. 计算方法与工程应用[J]. 水文地质工程地质, 1995(5): 46-50. Yang Min, Wang Rui-xiang, Feng You-quan. Design of retaining wall structures for excavations: I. theory and application[J]. Hydrogeology and Engineering Geology, 1995(5): 46-50. [本文引用:1]
[3]	杨敏, 王瑞祥, 冯又全. 基坑挡墙结构的设计: II. 分析与讨论[J]. 水文地质工程地质, 1996(5): 15-19. Yang Min, Wang Rui-xiang, Feng You-quan. Design of retaining wall structures for excavations: II. analysis and discussion[J]. Hydrogeology and Engineering Geology, 1996(5): 15-19. [本文引用:1]
[4]	Matusi Tanotsu, Hong Won Pyo, Ito Tomio. Earth pressures on piles in a row due to lateral soil movements[J]. Soils and Foundations, 1982, 22(2): 71-80. [本文引用:1]
[5]	贾海莉, 王成华, 李江洪. 基于土拱效应的抗滑桩与护壁桩的桩间距分析[J]. 工程地质学报, 2004, 12(1): 98-103. Jia Hai-li, Wang Cheng-hua, Li Jiang-hong. Analysis of pile spacing between anti-sliding piles and pertaining piles in accordance with soil arching effect[J]. Journal of Engineering Geology, 2004, 12(1): 98-103. [本文引用:1]
[6]	蒋良潍, 黄润秋, 蒋忠信. 黏性土桩间土拱效应计算与桩间距分析[J]. 岩土力学, 2006, 27(3): 445-450. Jiang Liang-wei, Huang Run-qiu, Jiang Zhong-xin. Analysis of soil arching effect between adjacent piles and their spacing in cohesive soils[J]. Rock and Soil Mechanics, 2006, 27(3): 445-450. [本文引用:1]
[7]	Ito T, Matsui T. Methods to estimate lateral force acting on stabilizing piles[J]. Soils and Foundations, 1975, 15(4): 43-59. [本文引用:1]
[8]	古海东, 杨敏. 疏排桩-土钉墙组合支护结构排桩荷载分担比试验研究[J]. 建筑结构学报, 2014, 35(2): 102-110. Gu Hai-dong, Yang Min. Experimental study on pile load sharing ratio of composite structure with scattered piles and soil nailing[J]. Journal of Building Structures, 2014, 35(2): 102-110. [本文引用:3]

0.0

... 0 引言深基坑支护结构设计一直以来都是岩土工程领域里的一个热点和难点问题,对于深基坑排桩支护结构,常用的设计方法有等值梁法和弹性地基梁法,目前,在工程设计中,多采用国家行业标准(JGJ120-2012)^[1]中的弹性支点法(m法),同济大学的杨敏在文献[2]中给出了弹性支点法(m法)的有限元实现过程,并编制和开发了相应的计算软件----同济启明星深基坑支挡结构分析计算软件,并采用该软件对维护结构变形和变形性状影响因素进行了分析和讨论^[3] ...

... 规范法^[1]中的计算模型对单根支护桩上的主动土压力计算宽度取为排桩间距 ...

... 为了验证三维有限元模型计算结果的合理性,将离心模型试验得出的桩身弯矩和桩身水平位移以及建筑基坑支护技术规程(JGJ120-2012)^[1]中的m法计算结果进行了对比分析,桩身弯矩和桩身水平位移分布图如图5和图6所示 ...

... 其中m法中m的取值采用规程^[1]中的推荐经验公式: ...

1995

0.0

1996

0.0

1982

0.0

... 只有当桩间土体的土压力完全通过土拱效应传递给排桩时,排桩计算宽度取桩间距才较为合理,然而,实际中土拱效应能否存在以及土拱效应能传递多少土压力给排桩还有待进一步的研究^[4,5,6,7] ...

2004

0.0

. 2004, 12(1):98-103 DOI:doi:10.3969/j.issn.1004-9665.2004.01.018

Analysis of pile spacing between anti-sliding piles and pertaining piles in accordance with soil arching effect

基于土拱效应的抗滑桩与护壁桩的桩间距分析

Jia Hai-li , Wang Cheng-hua , Li Jiang-hong.

贾海莉, 王成华, 李江洪

Anti-sliding pile are used to stabilize slopes and to control landslide for a long history. It is because of the soil arching effect between the piles that can work effectively. According to the limit equilibrium of the soil mass,the horizontal soil arching effect between the cylindrical anti-sliding piles in the earth is studied and the formula for largest spacing between the piles is proposed. Then, through a case study, the physical meanings and the feasibility of the largest spacing between the piles are discussed. Then the suitable spacing between the piles is proposed in consideration of the soil arching effect. Finally, Some useful suggestions for the slope engineering designing are also proposed in the paper.

抗滑桩与护壁桩分别在滑坡治理和基坑支护中发挥着巨大的作用 ,其实施正是利用了土中的成拱效应 ,然而传统桩的设计虽考虑土拱效应的存在 ,但桩间距确定理论与方法并未建立起来。本文首先基于土体的极限平衡条件对滑坡推力作用下的土体中的成拱作用进行研究 ,得出了抗滑桩的最大桩间距公式 ,并以某一具体工程为例 ,对该最大桩间距的物理意义和可用性进行了讨论。在此基础上 ,给出了在考虑土拱效应的情况下合理桩间距的确定方法 ,并以此为据 ,对边坡加固设计提出一些建议.

2006

0.0

. 2006, 27(3):445-450 DOI:doi:10.3969/j.issn.1000-7598.2006.03.021

Analysis of soil arching effect between adjacent piles and their spacing in cohesive soils

黏性土桩间土拱效应计算与桩间距分析

Jiang Liang-wei , Huang Run-qiu , Jiang Zhong-xin.

蒋良潍, 黄润秋, 蒋忠信

土拱效应是安全经济地发挥抗滑桩等非连续支挡结构的支护功能的重要前提,桩间距与成拱作用密切相关.利用合理拱轴线几何特征与受压破裂角方位,通过力学概念分析,将黏性土土拱计算的平衡条件和强度条件综合简化为以拱脚处拱圈轴向压应力表达的形式.继而从最少且最易获得的土工材料参数(内聚力c、内摩擦角()出发,根据轴向压应力与矢跨比函数关系,利用摩尔-库仑强度准则,推导了拱曲线与桩间距上下限的简便计算式,再以此进一步探讨了考虑土拱效应三维稳定的桩间距校核,并以工程实例验证,以对土拱效应的估算提供简便清晰的计算方法.

1975

0.0

2014

0.0

. 2014, 35(2):102-110

Experimental study on pile load sharing ratio of composite structure with scattered piles and soil nailing

疏排桩-土钉墙组合支护结构排桩荷载分担比试验研究

Gu Hai-dong , Yang Min.

古海东, 杨敏

Based on the results of ten groups centrifuge model tests for composite structure with scatlered piles and soil nailing, a calculation model of load sharing ratio for piles was proposed. In addition, the variation rules and influencing factors of pile load sharing ratio were analyzed and the simplified load sharing ratio calculation formula was given. The results of centrifuge tests show that when the excavation depths of pit is small, the load on supporting structure is mainly resisted by soil nailing and the bearing force of piles is small. With increase of excavation depths, piles bear more and more load up to more than 90% of the total load, since the soil arching effect passes the soil pressure within supporting structure to piles continuously. Increasing nail length and reducing nail spacing can reduce the bearing force of piles effectively, and improve the stability of the whole supporting structure significantly. Increasing pile spacing can reduce the load bearing ratio of piles, but too large pile spacing will reduce the stability of the entire supporting structure significantly. Effect of the vertical nail spacing on load sharing ration of piles is more obvious than the horizontal nail spacing.

对10个疏排桩-土钉墙组合支护结构进行离心机模型试验。基于试验结果，提出排桩荷载分担比的计算模型，探讨排桩荷载分担比的变化规律以及影响因素，并提出简化计算式。研究结果表明：当基坑挖深较小时，支护结构的荷载主要由土钉墙承担，排桩承担的荷载较小，随着开挖深度的增加，土拱效应将支护结构范围内的土压力不断传递给桩身，排桩承担的荷载越来越多，最多可达到总荷载的90%以上；增加土钉长度、减小土钉间距既可有效减少排桩分担的荷载，同时还能明显提高整个支护结构的整体稳定性；当桩间距在一定范围内时，增加桩间距能减小排桩荷载分担比，但是桩间距过大会明显降低整个支护结构的稳定性；土钉竖向间距对排桩荷载分担比的影响比土钉水平间距更为明显。

... 古海东等^[8]通过一组离心机模型试验分析了深基坑排桩支护结构的桩身内力分布情况以及支护结构破坏模式 ...

... 本文结合文献^[8]中的离心机模型试验建立了三维有限元模型,通过与离心模型试验的比较,验证了三维有限元模型的合理性,并探讨了规范法计算排桩内力的适宜性 ...

... 1 三维有限元方法可靠性验证古海东等^[8]通过一组离心机模型试验分析了深基坑排桩支护结构的桩身内力分布情况 ...