点接触正交变传动比面齿轮副重合度分析

引用本文

林超, 顾思家, 刘毅. 点接触正交变传动比面齿轮副重合度分析.吉林大学学报:工学版, 2016, 46(2): 471-478
LIN Chao, GU Si-jia, LIU Yi. Analysis of contact ratio of point contact orthogonal variable transmission ratio face gear. Journal of Jilin University Engineering and Technology Edition, 2016, 46(2): 471-478 复制到剪切板

Permissions

点接触正交变传动比面齿轮副重合度分析

林超, 顾思家, 刘毅

重庆大学机械传动国家重点实验室,重庆 400044

作者简介:林超(1958-),男,教授,博士生导师.研究方向:新型齿轮传动,机械设计计算机辅助工程,齿轮传动系统的设计与制造.E-mail:linchao@cqu.edu.cn

基金:国家自然科学基金项目(51275537)

摘要

为了改善正交变传动比面齿轮的传动质量与承载能力,研究了该齿轮副的基本几何参数对其重合度的影响.应用齿轮啮合原理,建立了正交变传动比面齿轮副的传动坐标系,推导出正交变传动比面齿轮副的节曲线及齿顶曲线方程.将正交变传动比面齿轮副传动展开成非圆齿轮齿条的传动形式,提出了点接触正交变传动比面齿轮副重合度的计算方法,分析了刀具齿轮及齿轮副的基本几何参数对其重合度的影响.通过测量试验得到的重合度与理论重合度的对比分析验证了该齿轮副重合度计算方法的正确性.

关键词: 机械设计; 重合度; 变传动比; 面齿轮; 齿条

中图分类号:TH132 文献标志码:A 文章编号:1671-5497(2016)02-0471-08

Analysis of contact ratio of point contact orthogonal variable transmission ratio face gear

LIN Chao, GU Si-jia, LIU Yi

State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China

Abstract

To improve the transmission quality and bearing capacity of orthogonal variable transmission ratio face gear, the influences of the geometric parameters of gear pair on the contact ratio are investigated. According to the spatial gear meshing theory, the meshing coordinate is established and the equations of the section curve and crest curve s are deduced. The orthogonal variable transmission ratio face gear is transformed to non-circular gear rack and pinion. The calculation method of the contact ratio is proposed, and the influences of the geometric parameters of cutter gear and gear pair on the contact ratio are analyzed. The proposed calculation method of the contact ratio is verified by the measurement experiment of the actual contact ratio.

Keyword: mechanical design; contact ratio; variable transmission ratio; face gear; pinion

Show Figures

0 引言

面齿轮传动是一种锥齿轮与柱齿轮相啮合的新型齿轮传动^[1], 当锥齿轮与柱齿轮的回转中心轴正交时, 则为正交面齿轮传动, 当正交面齿轮副中的面齿轮为正交变传动比面齿轮, 柱齿轮为非圆柱齿轮时, 为正交变传动比面齿轮传动, 简称为正交非圆面齿轮传动.正交非圆面齿轮传动集合了非圆柱齿轮, 非圆锥齿轮, 端面齿轮等的传动优点, 能实现相交轴之间的变传动比运动.该新型齿轮传动能实现点接触传动, 对安装误差不敏感, 具有良好的传动性能, 且可用现有机床加工, 因此具有很大的应用前景.目前, 国内外还没有开展关于此种新型面齿轮副重合度计算方面的研究工作, 极大地阻碍了对该齿轮副的强度, 传动特性, 动力学等的研究及其在航空航天等领域的应用^[1].正交非圆面齿轮副的重合度是评价该齿轮副的传动连续性, 确定轮齿载荷分配系数的依据^[2].齿轮副重合度也影响齿轮传动系统的啮合刚度^[3].国内学者针对用渐开线圆柱刀具齿轮加工的非圆柱齿轮进行了重合度方面的研究并提出了计算非圆齿轮重合度的不同方法^{[4, 5]}, 探索了高重合度弧齿锥齿轮的传动特性^[6], 分析了齿轮重合度对齿轮传动系统的动态传动特性的影响^[7].国外研究人员通过加载接触分析, 研究了齿轮在真实工况下的承载传动曲线误差和实际重合度, 并给出了弧齿锥齿轮传动误差和实际重合度的测量方法与结果^{[8, 9, 10]}.针对面齿轮副传动, 研究了其几何特性^{[11, 12]}, 提出了面齿轮副的加工方法^{[13, 14]}及其重合度计算公式^[15].

本文应用齿轮啮合原理, 将正交非圆面齿轮副传动展开成非圆齿轮齿条传动方式, 研究实现点接触的正交非圆面齿轮重合度的计算方法, 讨论正交非圆面齿轮副的几何参数对其重合度的影响, 通过试验验证正交非圆面齿轮副重合度计算方法的正确性.

1 齿轮副节曲线, 齿顶曲线的计算

1.1 齿轮副的传动原理

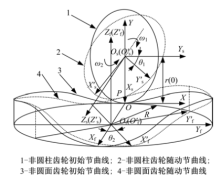
在正交非圆面齿轮副的传动过程中, 具体表现为非圆柱齿轮与非圆面齿轮的节曲线之间的纯滚动^[1], 建立如图1所示坐标系.

	Figure Option View Download New Window
	图1 齿轮副的坐标系Fig.1 Coordinate system of the gear pair

图1中 $\begin{matrix} O_{s} - X_{s} Y_{s} Z_{s} \end{matrix}$ 和 $\begin{matrix} O_{f} - X_{f} Y_{f} Z_{f} \end{matrix}$ 分别为非圆柱齿轮与非圆面齿轮的静坐标系, $\begin{matrix} O'_{s} - X'_{s} Y'_{s} Z'_{s} \end{matrix}$ 和 $\begin{matrix} O'_{f} - X'_{f} Y'_{f} Z'_{f} \end{matrix}$ 分别为非圆柱齿轮与非圆面齿轮的随动坐标系, 非圆柱齿轮为主动齿轮, 非圆面齿轮为从动齿轮, 非圆柱齿轮绕 $\begin{matrix} Z_{s} \end{matrix}$ 轴顺时针转动, 转角为 $\begin{matrix} θ_{1}, \end{matrix}$ 其在非圆柱齿轮随动节曲线上对应点为 $\begin{matrix} P, \end{matrix}$ 非圆面齿轮绕 $\begin{matrix} Z_{f} \end{matrix}$ 轴转动, 转角为 $\begin{matrix} θ_{2}, \end{matrix}$ 平面 $\begin{matrix} X_{s} Y_{s} \end{matrix}$ 到 $\begin{matrix} Z_{f} \end{matrix}$ 轴的距离为 $\begin{matrix} R, \end{matrix}$ 平面 $\begin{matrix} X_{f} Y_{f} \end{matrix}$ 到 $\begin{matrix} Z_{s} \end{matrix}$ 轴的距离为 $\begin{matrix} r (0), Z_{f} \end{matrix}$ 轴与 $\begin{matrix} Z_{s} \end{matrix}$ 轴垂直相交, $\begin{matrix} O - XY \end{matrix}$ 为固定在面齿轮机架上且在平面 $\begin{matrix} X_{s} Y_{s} \end{matrix}$ 内的平面坐标系.

1.2 非圆柱齿轮齿顶曲线, 齿根曲线表示

非圆柱齿轮的节曲线为高阶椭圆, 在随动坐标系 $\begin{matrix} O'_{s} - X'_{s} Y'_{s} \end{matrix}$ 中其极坐标方程表示为:

$\begin{matrix} r (θ_{1}) = \frac{a (1 - k^{2})}{1 - kcos (n_{1} θ_{1})} \end{matrix}$ (1)

式中: $\begin{matrix} θ_{1} 、 a 、 k 、 n_{1} \end{matrix}$ 分别为非圆柱齿轮的转角, 长半轴, 偏心率, 阶数.

非圆柱齿轮的齿顶曲线为节曲线向外的法向距离为齿顶高 $\begin{matrix} h_{a} \end{matrix}$ 的等距曲线, 齿根曲线为节曲线向内的法向距离为齿根高 $\begin{matrix} h_{f} \end{matrix}$ 的等距曲线, 如图2所示.

	Figure Option View Download New Window
	图2 非圆柱齿轮的坐标系Fig.2 Coordinate system of non-cylindrical gear

非圆柱齿轮的节曲线在随动坐标系 $\begin{matrix} O'_{s} - X'_{s} Y'_{s} Z'_{s} \end{matrix}$ 中的矢量表示为:

$\begin{matrix} {[r_{s}]}_{O'_{s}} = [\begin{matrix} r (θ_{1}) \cos (θ_{1}) \\ r (θ_{1}) \sin (θ_{1}) \\ 0 \\ 1 \end{matrix}] \end{matrix}$ (2)

非圆柱齿轮的齿顶曲线在随动坐标系 $\begin{matrix} O'_{s} - X'_{s} Y'_{s} Z'_{s} \end{matrix}$ 中的矢量表示为:

$\begin{matrix} {[r_{sa}]}_{O'_{s}} = [\begin{matrix} r_{1} \cos (θ_{1} + λ_{1}) \\ r_{1} \sin (θ_{1} + λ_{1}) \\ 0 \\ 1 \end{matrix}] \end{matrix}$ (3)

式中: $\begin{matrix} r_{1} = \sqrt[]{r^{2} (θ_{1}) + {h_{a}}^{2} + 2 h_{a} r (θ_{1}) sinμ}, h_{a} = m h_{a}^{*}, m \end{matrix}$ 为刀具齿轮模数, 即非圆柱齿轮模数, $\begin{matrix} h_{a}^{*} \end{matrix}$ 为刀具齿轮齿顶高系数, 即非圆柱齿轮齿顶高系数; $\begin{matrix} λ_{1} = \arccos [({r_{1}}^{2} + r^{2} (θ_{1}) - {h_{a}}^{2}) / (2 r_{1} r (θ_{1}))]; \end{matrix}$

$\begin{matrix} μ = \arctan (r (θ_{1}) / r' (θ_{1})); r' (θ_{1}) = dr (θ_{1}) / d θ_{1} 。 \end{matrix}$

非圆柱齿轮的齿根曲线在随动坐标系 $\begin{matrix} O'_{s} - X'_{s} Y'_{s} \end{matrix}$ 中的矢量表示为:

$\begin{matrix} {[r_{sf}]}_{O'_{s}} = [\begin{matrix} r_{2} \cos (θ_{1} - λ_{2}) \\ r_{2} \sin (θ_{1} - λ_{2}) \\ 0 \\ 1 \end{matrix}] \end{matrix}$ (4)

式中: $\begin{matrix} r_{2} = \sqrt[]{r^{2} (θ_{1}) + {h_{f}}^{2} - 2 h_{f} r (θ_{1}) sinμ}, h_{f} = m {h_{f}}^{*}, {h_{f}}^{*} \end{matrix}$ 为刀具齿轮齿根高系数, 即非圆柱齿轮齿根高系数; $\begin{matrix} λ_{2} = \arccos [({r_{2}}^{2} + r^{2} (θ_{1}) - {h_{f}}^{2}) / (2 r_{2} r (θ_{1}))] 。 \end{matrix}$

1.3 非圆面齿轮节曲线, 齿顶曲线表示

根据图1中所示齿轮副的相互运动关系, 非圆柱齿轮的随动坐标系 $\begin{matrix} O'_{s} - X'_{s} Y'_{s} Z'_{s} \end{matrix}$ 到正交非圆面齿轮的随动坐标系 $\begin{matrix} O'_{f} - X'_{f} Y'_{f} Z'_{f} \end{matrix}$ 的坐标变换矩阵为^[1]:

$\begin{matrix} \begin{matrix} M_{O'_{f}, O'_{s}} = \\ [\begin{matrix} - \sin (θ_{1}) \sin (θ_{2}) & \cos (θ_{1}) \sin (θ_{2}) & \cos (θ_{2}) & - Rcos (θ_{2}) \\ - \sin (θ_{1}) \cos (θ_{2}) & \cos (θ_{1}) \cos (θ_{2}) & - \sin (θ_{2}) & Rsin (θ_{2}) \\ - \cos (θ_{1}) & - s in (θ_{1}) & 0 & r (0) \\ 0 & 0 & 0 & 1 \end{matrix}] \end{matrix} \end{matrix}$ (5)

式中: $\begin{matrix} R = \frac{n_{2}}{2 π} \int_{0}^{\frac{2 π}{n_{1}}} r (θ_{1}) d θ_{1}; θ_{2} = \frac{1}{R} \int_{0}^{θ_{1}} r (θ) dθ 。其中的 θ_{2} 、 n_{2} \end{matrix}$ 分别为非圆面齿轮的转角与阶数, $\begin{matrix} R \end{matrix}$ 为非圆面齿轮节曲线所在圆柱面半径.

非圆面齿轮的节曲线在非圆面齿轮随动坐标系 $\begin{matrix} O'_{f} - X'_{f} Y'_{f} Z'_{f} \end{matrix}$ 中表示为:

$\begin{matrix} {[r_{f}]}_{O'_{f}} = M_{O'_{f}, O'_{s}} {[r_{s}]}_{O'_{s}} = [\begin{matrix} - Rcos (θ_{2}) \\ Rsin (θ_{2}) \\ r (0) - r (θ_{1}) \\ 1 \end{matrix}] \end{matrix}$ (6)

非圆面齿轮的齿顶曲线为半径为 $\begin{matrix} R \end{matrix}$ 的圆柱面与非圆面齿轮的齿顶曲面相交形成的空间曲线^[1], 非圆面齿轮的齿顶曲面根据非圆面齿轮的加工原理可理解为非圆柱齿轮的齿根曲面的啮合曲面, 其在非圆面齿轮随动坐标系 $\begin{matrix} O'_{f} - X'_{f} Y'_{f} Z'_{f} \end{matrix}$ 中表示为:

$\begin{matrix} \begin{matrix} {[r_{fa}]}_{O'_{f}} = \\ [\begin{matrix} - \frac{1}{2} r_{2} (\cos (θ_{2} - λ_{2}) - \cos (θ_{2} + λ_{2})) + (u_{k} - R) \cos (θ_{2}) \\ \frac{1}{2} r_{2} (\sin (θ_{2} - λ_{2}) - \sin (θ_{2} + λ_{2})) - (u_{k} - R) \sin (θ_{2}) \\ - r_{2} \cos (λ_{2}) + r (0) \\ 1 \end{matrix}] \end{matrix} \end{matrix}$ (7)

式中: $\begin{matrix} u_{k} \end{matrix}$ 为标记非圆柱齿轮沿旋转轴方向上齿根曲面的参数.在式(7)中, 当 $\begin{matrix} u_{k} = 0 \end{matrix}$ 时, 表示非圆面齿轮的齿顶曲线.

2 齿轮副的重合度计算

2.1 齿轮副的齿轮齿条形式及重合度表示

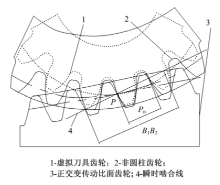
正交非圆面齿轮副均由渐开线圆柱齿轮加工而来, 在传动过程中, 正交非圆面齿轮副实现点接触传动^[1], 在其啮合时, 总是非圆柱齿轮的齿根与非圆面齿轮的齿顶处进入啮合, 非圆柱齿轮的齿顶与非圆面齿轮的齿根处退出啮合, 且接触点在非圆柱齿轮节曲线所在截面内^[14], 因此可利用机械设计的反转原理, 将齿轮副的节曲线与齿顶曲线展开到非圆柱齿轮节曲线所在的固定坐标系中, 即将正交非圆面齿轮副传动转换成非圆齿轮齿条传动, 见图3.

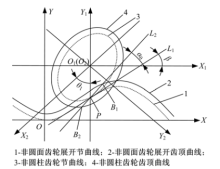
	Figure Option View Download New Window
	图3 齿轮副的齿轮齿条展开形式Fig.3 Rack and pinion expanded form of the gear pair

如图3所示, 平面坐标系 $\begin{matrix} O - XY \end{matrix}$ 为面齿轮节曲线展开后的固定坐标系, 坐标系 $\begin{matrix} O_{1} - X_{1} Y_{1} \end{matrix}$ 为固定在非圆柱齿轮的转动中心上的固定坐标系, 非圆柱齿轮的转动中心在坐标系 $\begin{matrix} O - XY \end{matrix}$ 的位置为 $\begin{matrix} (R θ_{2}, r (0)), \end{matrix}$ 坐标系 $\begin{matrix} O_{2} - X_{2} Y_{2} \end{matrix}$ 为非圆柱齿轮的随动坐标系, $\begin{matrix} O_{1} \end{matrix}$ 与 $\begin{matrix} O_{2} \end{matrix}$ 重合. $\begin{matrix} P \end{matrix}$ 点为非圆柱齿轮与正交变传动比面齿轮节曲线的啮合点, $\begin{matrix} P \end{matrix}$ 点的坐标为 $\begin{matrix} (R θ_{2}, r (0) - r (θ_{1})) \end{matrix}$ , 曲线3为非圆柱齿轮的节曲线, 曲线4为非圆柱齿轮的齿顶曲线, 直线 $\begin{matrix} L_{1} \end{matrix}$ 为在 $\begin{matrix} P \end{matrix}$ 点处非圆柱齿轮节曲线与正交变传动比面齿轮节曲线的公切线, 直线 $\begin{matrix} L_{2} \end{matrix}$ 为非圆柱齿轮与非圆面齿轮齿廓啮合点与 $\begin{matrix} P \end{matrix}$ 点的线段所在的直线(即瞬时啮合线)^[3], 且直线 $\begin{matrix} L_{1} \end{matrix}$ 与直线 $\begin{matrix} L_{2} \end{matrix}$ 之间的夹角为刀具齿轮的压力角 $\begin{matrix} α_{0} \end{matrix}$ ^[3].直线 $\begin{matrix} L_{2} \end{matrix}$ 与正交变传动比面齿轮的齿顶曲线和非圆柱齿轮的齿顶曲线分别相交于 $\begin{matrix} B_{1} 、 B_{2}, \end{matrix}$ 则线段 $\begin{matrix} \overset{B_{2}}{B_{1}} \end{matrix}$ 为此瞬时的啮合线段, 则正交非圆面齿轮副在 $\begin{matrix} P \end{matrix}$ 点处的重合度 $\begin{matrix} ε_{P} \end{matrix}$ 为:

$\begin{matrix} ε_{P} = \frac{\overset{B_{2}}{B_{1}}}{P_{n}} \end{matrix}$ (8)

正交非圆面齿轮副与刀具齿轮的法向齿距的具体关系如图4所示, 则面齿轮的法向齿距 $\begin{matrix} P_{n} \end{matrix}$ 为:

$\begin{matrix} P_{n} = πmcos (α_{0}) \end{matrix}$ (9)

	Figure Option View Download New Window
	图4 齿轮副的法向齿距Fig.4 Normal pitch of the gear pair

2.2 齿轮副齿顶曲线的展开

由图3可得非圆柱齿轮的随动坐标系 $\begin{matrix} O_{2} - X_{2} Y_{2} \end{matrix}$ 到非圆柱齿轮的固定坐标系 $\begin{matrix} O_{1} - X_{1} Y_{1} \end{matrix}$ 的坐标变换矩阵为:

$\begin{matrix} M_{O_{1}, O_{2}} = [\begin{matrix} - \sin (θ_{1}) & \cos (θ_{1}) & 0 \\ - \cos (θ_{1}) & - \sin (θ_{1}) & 0 \\ 0 & 0 & 1 \end{matrix}] \end{matrix}$ (10)

非圆柱齿轮的固定坐标系 $\begin{matrix} O_{1} - X_{1} Y_{1} \end{matrix}$ 到其固定坐标系 $\begin{matrix} O - XY \end{matrix}$ 的坐标变换矩阵为:

$\begin{matrix} M_{O, O_{1}} = [\begin{matrix} 1 & 0 & R θ_{2} \\ 0 & 1 & r (0) \\ 0 & 0 & 1 \end{matrix}] \end{matrix}$ (11)

非圆柱齿轮的随动坐标系 $\begin{matrix} O_{2} - X_{2} Y_{2} \end{matrix}$ 到其固定坐标系 $\begin{matrix} O - XY \end{matrix}$ 的坐标变换矩阵为:

$\begin{matrix} M_{O, O_{2}} = [\begin{matrix} - \sin (θ_{1}) & \cos (θ_{1}) & R θ_{2} \\ - \cos (θ_{1}) & - \sin (θ_{1}) & r (0) \\ 0 & 0 & 1 \end{matrix}] \end{matrix}$ (12)

结合式(3)可得非圆柱齿轮的齿顶曲线在固定坐标系 $\begin{matrix} O - XY \end{matrix}$ 中表示为:

$\begin{matrix} {[r_{sf}]}_{O} = [\begin{matrix} rsin (θ + λ - θ_{1}) + R θ_{2} \\ - rcos (θ + λ - θ_{1}) + r (0) \\ 1 \end{matrix}] \end{matrix}$ (13)

式中: $\begin{matrix} r 、 λ \end{matrix}$ 的计算与 $\begin{matrix} r_{1} 、 λ_{1} \end{matrix}$ 的计算相同, 仅用极角 $\begin{matrix} θ \end{matrix}$ 代换转角 $\begin{matrix} θ_{1}, θ \in [0, 2 π] 。 \end{matrix}$

如图3所示, 在固定坐标系 $\begin{matrix} O - XY \end{matrix}$ 中将非圆面齿轮齿顶曲线展开, 由式(7)可得非圆面齿轮齿顶曲线在平面坐标系 $\begin{matrix} O - XY \end{matrix}$ 中表示为:

$\begin{matrix} \{\begin{matrix} x = Rθ'_{2} = \int_{0}^{θ} r (θ) dθ \\ y = r (0) - r'_{2} \cos (λ'_{2}) \end{matrix} \end{matrix}$ (14)

式中: $\begin{matrix} θ'_{1} 、 θ'_{2} 、 r'_{2} 、 λ'_{2} \end{matrix}$ 的计算与 $\begin{matrix} θ_{1} 、 θ_{2} 、 r_{2} 、 λ_{2} \end{matrix}$ 相同, 仅用极角 $\begin{matrix} θ'_{1} \end{matrix}$ 代换转角 $\begin{matrix} θ_{1}, θ'_{1} \in [0, 2 π] 。 \end{matrix}$

2.3 齿轮副重合度计算

图3中直线 $\begin{matrix} L_{1} \end{matrix}$ 与 $\begin{matrix} X \end{matrix}$ 轴的夹角为 $\begin{matrix} β, \end{matrix}$ 直线 $\begin{matrix} L_{2} \end{matrix}$ 与直线 $\begin{matrix} L_{1} \end{matrix}$ 之间的夹角为 $\begin{matrix} α_{0}, \end{matrix}$ 则直线 $\begin{matrix} L_{2} \end{matrix}$ 与 $\begin{matrix} X \end{matrix}$ 轴的夹角为 $\begin{matrix} β + α_{0}, \end{matrix}$ 由图3可知 $\begin{matrix} β \end{matrix}$ 的表达如下:

$\begin{matrix} β = \arctan (r (θ_{1}) / r' (θ_{1})) - \frac{π}{2} \end{matrix}$ (15)

则直线 $\begin{matrix} L_{2} \end{matrix}$ 在固定坐标系 $\begin{matrix} O - XY \end{matrix}$ 中表示为:

$\begin{matrix} y_{L_{2}} - (r (0) - r (θ_{1})) = t an (β + α_{0}) (x_{L_{2}} - R θ_{2}) \end{matrix}$ (16)

直线 $\begin{matrix} L_{2} \end{matrix}$ 与非圆面齿轮的齿顶曲线的交点(即 $\begin{matrix} B_{1} \end{matrix}$ )坐标如下表示:

$\begin{matrix} \{\begin{matrix} y_{B_{1}} - (r (0) - r (θ_{1})) = \tan (β + α_{0}) (x_{B_{1}} - R θ_{2}) \\ x_{B_{1}} = \int_{0}^{θ} r (θ) dθ \\ y_{B_{1}} = r (0) - r'_{2} \cos (λ'_{2}) \end{matrix} \end{matrix}$ (17)

直线 $\begin{matrix} L_{2} \end{matrix}$ 与非圆柱齿轮的齿顶曲线的交点(即 $\begin{matrix} B_{2} \end{matrix}$ )坐标如下表示:

$\begin{matrix} \{\begin{matrix} y_{B_{2}} - (r (0) - r (θ_{1})) = \tan (β + α_{0}) (x_{B_{2}} - R θ_{2}) \\ x_{B_{2}} = r \sin (θ + λ - θ_{1}) + R θ_{2} \\ y_{B_{2}} = - rcos (θ + λ - θ_{1}) + r (0) \end{matrix} \end{matrix}$ (18)

通过式(17)(18)可以求得 $\begin{matrix} B_{1} 、 B_{2} \end{matrix}$ 的坐标 $\begin{matrix} (x_{B_{1}} (θ_{1}), y_{B_{1}} (θ_{1})) 、 (x_{B_{2}} (θ_{1}), y_{B_{2}} (θ_{1})), \end{matrix}$ 则正交非圆面齿轮副在非圆柱齿轮转角为 $\begin{matrix} θ_{1} \end{matrix}$ 时的重合度为:

$\begin{matrix} \begin{matrix} ε (θ_{1}) = \\ \frac{\sqrt[]{(x_{B_{1}} (θ_{1}) - x_{B_{2}} (θ_{1} {))}^{2} + (y_{B_{1}} (θ_{1}) - y_{B_{2}} (θ_{1} {))}^{2}}}{πmcos (α_{0})} \end{matrix} \end{matrix}$ (19)

正交变传动比面齿轮副的平均重合度 $\begin{matrix} ε \end{matrix}$ 为:

$\begin{matrix} ε = \int_{0}^{\frac{2 π}{n_{1}}} ε (θ_{1}) d θ_{1} \end{matrix}$ (20)

3 齿轮副的重合度分析

3.1 刀具齿轮参数对重合度的影响

由式(19)可知, 刀具齿轮的模数 $\begin{matrix} m 、 \end{matrix}$ 压力角 $\begin{matrix} α_{0} 、 \end{matrix}$ 齿顶高系数 $\begin{matrix} h_{a}^{*} \end{matrix}$ 对齿轮副的重合度有影响.现取非圆柱齿轮的偏心率 $\begin{matrix} k = 0.1 \end{matrix}$ 和阶数 $\begin{matrix} n_{1} = 2, \end{matrix}$ 齿数 $\begin{matrix} z_{1} = 18, \end{matrix}$ 非圆面齿轮的阶数 $\begin{matrix} n_{2} = 4 。 \end{matrix}$ 固定刀具齿轮的其中两个参数, 改变另外一个参数即可研究该参数对齿轮副重合度的影响.刀具齿轮各参数取值如表1所示.

表1 刀具齿轮基本参数表 Tabel 1 Basic parameters of cutter gear

研究内容	α ₀/(° )	m	$\begin{matrix} h_{a}^{*} \end{matrix}$
α ₀对重合度的影响	18, 20, 22.5	4	1
m对重合度的影响	20	2, 3, 4	1
$\begin{matrix} h_{a}^{*} \end{matrix}$ 对重合度的影响	20	4	0.8, 0.9, 1

表1 刀具齿轮基本参数表 Tabel 1 Basic parameters of cutter gear

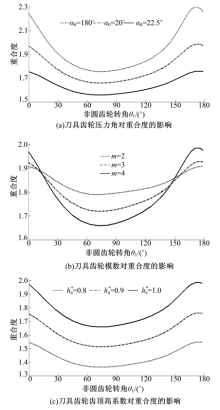
结合式(15)~(20), 编程计算出刀具齿轮的模数m、压力角α₀ 、齿顶高系数h_a^*取表1中各值时的重合度, 齿轮副重合度在一个周期内的变化规律如图5所示.

	Figure Option View Download New Window
	图5 刀具齿轮基本参数对重合度的影响Fig.5 Impacts of basic parameters of cutter gear to contact ratio

由图5(a)可知:齿轮副的重合度随着刀具齿轮的压力角的增大而减小, 不同压力角[18° , 20° , 22.5° ]对应的平均重合度为[1.932, 1.777, 1.636].由此可知, 当需要增大齿轮副的重合度时, 可以适当地减小刀具齿轮的压力角.

由图5(b)可知:齿轮副的最大重合度随着刀具齿轮的模数的增大而增大, 最小重合度随着刀具齿轮的模数的增大而减小.不同模数[2, 3, 4]对应的平均重合度为[1.835, 1.799, 1.777].由此可知, 当需要增大齿轮副的重合度时, 可以适当地减小刀具齿轮的模数.

由图5(c)可知:齿轮副的重合度随着刀具齿轮的齿顶高系数的增大而增大, 不同齿顶高系数[0.8, 0.9, 1.0]对应的平均重合度为[1.435, 1.606, 1.777].因此, 在工程应用中可以适当地增加齿轮副的齿顶高, 从而使齿轮副获得更大的重合度, 提高齿轮副的传动质量.

3.2 非圆柱齿轮参数对重合度的影响

非圆齿轮的基本参数包括偏心率 $\begin{matrix} k 、 \end{matrix}$ 阶数 $\begin{matrix} n_{1} \end{matrix}$ 和齿数 $\begin{matrix} z_{1}, \end{matrix}$ 其中, 取刀具齿轮的基本参数模数 $\begin{matrix} m = 4 \end{matrix}$ , 压力角 $\begin{matrix} α_{0} = 20 ° 、 \end{matrix}$ 齿顶高系数 $\begin{matrix} h_{a}^{*} = 1, \end{matrix}$ 非圆面齿轮的阶数 $\begin{matrix} n_{2} = 4 。 \end{matrix}$ 当加工非圆齿轮的刀具齿轮的模数确定时, 非圆齿轮的齿数变化反映在非圆柱齿轮节曲线的长半轴 $\begin{matrix} a \end{matrix}$ 的变化上^[1].其长半轴 $\begin{matrix} a \end{matrix}$ 需满足:

$\begin{matrix} \int_{0}^{2} \sqrt[]{r (θ_{1})^{2} + r' (θ_{1})^{2}} d θ_{1} = m z_{1} \end{matrix}$ (21)

固定非圆柱齿轮的其中两个参数, 改变另外一个参数即可研究该参数对齿轮副重合度的影响.非圆柱齿轮的各参数的取值如表2所示.

表2 非圆柱齿轮基本参数表 Tabel 2 Basic parameters of non-cylindrical gear

结合式(15)~(21), 编程计算出非圆柱齿轮的偏心率 k和阶数n₁,齿数z₁取表2中各值时的重合度, 得到齿轮副的重合度随其变化的规律, 如图6所示.

	Figure Option View Download New Window
	图6 非圆柱齿轮基本参数对重合度的影响Fig.6 Impacts of basic parameters of non-cylindrical gear to contact ratio

由图6(a)可知:随着非圆柱齿轮偏心率 $\begin{matrix} k \end{matrix}$ 的增加, 正交非圆面齿轮副的最大重合度变大, 最小重合度变小.不同偏心率[0.050, 0.075, 0.100]对应的平均重合度为[1.759, 1.766, 1.777].

由图6(b)可知:随着非圆柱齿轮阶数 $\begin{matrix} n_{1} \end{matrix}$ 的增加, 正交变传动比面齿轮副的最大重合度变大, 且重合度的变化周期为 $\begin{matrix} 2 π / n_{1} 。 \end{matrix}$ 不同非圆柱齿轮阶数[2, 3, 4]对应的平均重合度为[1.777, 1.865, 1.954].

由图6(c)可知:随着非圆柱齿轮齿数 $\begin{matrix} z_{1} \end{matrix}$ 的增加, 正交变传动比面齿轮副的最大重合度变小, 最小重合度变大, 但变化很小, 不同非圆柱齿轮齿数[18, 20, 22]对应的平均重合度为[1.777, 1.784, 1.792].

当确定了加工刀具与非圆柱齿轮的基本参数时, 再取定非圆面齿轮的阶数, 则非圆面齿轮唯一确定, 即非圆面齿轮的基本参数中, 唯一可能影响齿轮副重合度的基本参数为其阶数 $\begin{matrix} n_{2}, \end{matrix}$ 由式(15)~(20)可知, 非圆面齿轮的阶数 $\begin{matrix} n_{2} \end{matrix}$ 对齿轮副的重合度没有影响.

4 试验验证

选定齿轮副的基本参数为: $\begin{matrix} m = 4, k = 0.1, z_{1} = 18, \end{matrix}$ 在三轴数控铣床上加工出4阶非圆面齿轮与2阶非圆柱齿轮.利用德国克林贝格公司的P26全自动CNC控制齿轮测量中心测量正交非圆面齿轮副的齿面坐标, 如图7所示.

	Figure Option View Download New Window
	图7 齿轮副的测量试验Fig.7 Measurement experiment of the gear pair

对齿轮副中的非圆柱齿轮轮齿进行编号, 利用齿轮副测量试验, 提取出在随动坐标系 $\begin{matrix} O'_{s} - X'_{s} Y'_{s} Z'_{s} \end{matrix}$ 中非圆柱齿轮节曲线所在截面上第 $\begin{matrix} i \end{matrix}$ 齿的啮合面上的齿根与齿顶的平面坐标 $\begin{matrix} (x_{fi}, y_{fi}) 、 (x_{ai}, y_{ai}), \end{matrix}$ 提取出在随动坐标系 $\begin{matrix} O'_{f} - X'_{f} Y'_{f} Z'_{f} \end{matrix}$ 中正交变传动比面齿轮与非圆柱齿轮第 $\begin{matrix} i \end{matrix}$ 齿相啮合的啮合齿面上的齿根与齿顶坐标 $\begin{matrix} z_{fi} 、 z_{ai}, \end{matrix}$ 令:

$\begin{matrix} \{\begin{matrix} r (0) - \cos (θ_{fi} - θ_{i 1}) \sqrt[]{{x_{fi}}^{2} + {y_{fi}}^{2}} = z_{ai} \\ r (0) - \cos (θ_{ai} - θ_{i 2}) \sqrt[]{{x_{ai}}^{2} + {y_{ai}}^{2}} = z_{fi} \end{matrix} \end{matrix}$ (22)

方程 $\begin{matrix} r_{1} \cos (θ_{1} + λ_{1}) = x_{ai} \end{matrix}$ 中 $\begin{matrix} θ_{1} \end{matrix}$ 的解为 $\begin{matrix} θ_{ai}, \end{matrix}$ 方程 $\begin{matrix} r_{2} \cos (θ_{1} - λ_{2}) = x_{fi} \end{matrix}$ 中 $\begin{matrix} θ_{1} \end{matrix}$ 的解为 $\begin{matrix} θ_{fi} 。 \end{matrix}$

通过方程(21)可求得第 $\begin{matrix} i \end{matrix}$ 齿的节曲线所对应的非圆柱齿轮的齿转角 $\begin{matrix} θ_{i 0}, \end{matrix}$ 通过方程(22)可求得第 $\begin{matrix} i \end{matrix}$ 齿的啮入转角 $\begin{matrix} θ_{i 1} 、 \end{matrix}$ 啮出转角 $\begin{matrix} θ_{i 2}, \end{matrix}$ 则根据文献[14]可得第 $\begin{matrix} i \end{matrix}$ 齿的试验重合度 $\begin{matrix} ε_{i} \end{matrix}$ 为:

$\begin{matrix} ε_{i} = \frac{θ_{i 2} - θ_{i 1}}{θ_{i 0}} \end{matrix}$ (23)

由式(15)~(21)求得非圆柱齿轮第 $\begin{matrix} i \end{matrix}$ 齿的节曲线中点处的瞬时重合度作为第 $\begin{matrix} i \end{matrix}$ 齿的理论重合度, 将一个周期的理论重合度与试验重合度进行对比, 如表3所示.

表3 试验重合度与理论重合度 Tabel 3 Experimental and theoretical contact ratio

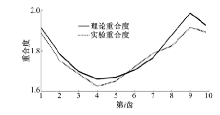
因第1齿与第10齿的重合度相同, 则可得图8.由表3和图8可知:试验重合度与理论重合度存在差异是因为齿轮副存在加工误差, 测量误差以及在选取齿轮副的齿根与齿顶坐标时有一定的偏差.试验重合度与理论重合度的变化趋势相似, 且每齿的试验重合度与理论重合度的绝对误差均小于0.07, 试验重合度与理论重合度误差均在4%以内.由此证明了正交非圆面齿轮副重合度的计算方法的正确性.

	Figure Option View Download New Window
	图8 试验重合度与理论重合度Fig.8 Experimental and theoretical contact ratio

5 结束语

应用齿轮啮合原理, 将正交非圆面齿轮传动转换成非圆齿轮齿条传动, 从几何学的角度推导了点接触正交非圆面齿轮副重合度的计算公式, 分析了刀具齿轮和正交非圆面齿轮副的基本几何参数对其重合度的影响.结果表明:刀具齿轮的压力角, 齿顶高系数, 非圆柱齿轮的阶数对重合度的影响较大.在正交非圆面齿轮副的设计过程中, 应合理选择刀具齿轮与非圆柱齿轮的基本几何参数, 从而限制齿轮副的最小重合度或增加平均重合度.通过试验结果的对比分析, 验证了该面齿轮副重合度计算公式的正确性, 得到了正交非圆面齿轮副重合度的变化规律.

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	龚海. 正交非圆面齿轮副的传动设计与特性分析[D]. 重庆: 重庆大学机械工程学院, 2012. Gong Hai. Transmission design and characteristic analysis of orthogonal non-circular face gear drive[D]. Chongqing: College of Mechanical Engineering, Chongqing University, 2012. [本文引用:7]
[2]	邓效忠, 方宗德. 弧齿锥齿轮的齿距误差对传动性能的影响研究[J]. 航空动力学报, 2002, 17(2): 268-272. Deng Xiao-zhong, Fang Zong-de. Study on contact ratio of spiral bevel gears and influence of pitch error[J]. Journal of Aerospace Power, 2002, 17(2): 265-272. [本文引用:1]
[3]	刘志峰, 张志民, 张敬莹, 等. 基于多项式的等高齿锥齿轮时变啮合刚度建模[J]. 吉林大学学报: 工学版, 2013, 43(4): 939-944. Liu Zhi-feng, Zhang Zhi-min, Zhang Jing-ying, et al. Moelling of high-spiral bevel gear mesh stiffness based on polynomial[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(4): 939-944. [本文引用:3]
[4]	聂玲. 椭圆锥齿轮啮合特性及其承载能力分析[D]. 重庆: 重庆大学机械工程学院, 2013. Nie Ling. Meshing characteristics and load capacity analysis of elliptical bevel gear[D]. Chongqing: College of Mechanical Engineering, Chongqing University, 2013. [本文引用:1]
[5]	王雷, 张瑞. 基于啮合角函数的非圆齿轮重合度求解[J]. 机械传动, 2009, 33(2): 14-19. Wang Lei, Zhang rui. Research on a novel transmission mechanism based on the principle of space curve mesh[J]. Journal of Mechanical Transmission, 2009, 33(2): 14-19. [本文引用:1]
[6]	邓效忠, 方宗德. 高重合度弧齿锥齿轮的性能分析与试验研究[J]. 航空动力学报, 2003, 18(6): 744-748. Deng Xiao-zhong, Fang Zong-de. Analysis of meshing behavior and experiments of spiral bevel gears with high contact ratio[J]. Journal of Aerospace Power, 2003, 18(6): 744-748. [本文引用:1]
[7]	陈安华, 罗善明, 王文明, 等. 齿轮系统动态传递误差和振动稳定性的数值研究[J]. 机械工程学报, 2004, 40(4): 21-25. Chen An-hua, Luo Shan-ming, Wang Wen-ming, et al. Numerical investigations on dynamic transmission error and stability of a geared rotor-bearing system[J]. Chinese Journal of Mechanical engineering, 2004, 40(4): 21-25. [本文引用:1]
[8]	Gosselin C, Cloutier L, Nguyen Q D. A general formulation for the calculation of the load sharing and transmission error under load sharing and transmission error under load of spiral bevel and hypoid gears[J]. Mech Mach Theory, 1995, 30(3): 433-450. [本文引用:1]
[9]	Gosselin C, Gagnon P, Cloutier L. Accurate tooth stiffness of spiral bevel gear teeth by the finite strip method[J]. Journal of Mechanical Design, 1998, 120(4): 599-605. [本文引用:1]
[10]	Sugimoto M, Maruyama N. Effect of tooth contact and gear dimensions on transmission errors of loaded hypoid gears[J]. Journal of Mechanical Design, 1991, 113(2): 182-187. [本文引用:1]
[11]	Cui Y M, Fang Z D, Su J Z, et al. Precise modeling of arc tooth face-gear with transition curve[J]. Chinese Journal of Aeronautics, 2013, 26(5): 1346-1351. [本文引用:1]
[12]	Litvin F L, Zhang Y, Wang J C, et al. Design and geometry of face-gear drives[J]. Journal of Mechanical Design, 1992, 114(4): 642-647. [本文引用:1]
[13]	Zanzi C, Pedrero J I. Application of modified geometry of face gear drive[J]. Computer Methods in Applied Mechanics and Engineering, 2005, 194(27-29): 3047-3066. [本文引用:1]
[14]	Litvin F L. Gear Geometry and Applied Theory[M]. Englewood Cliffs, New Jersey: Prentice Hall, Inc. , 1994. [本文引用:2]
[15]	Litvin F L, Gonzalez-Perez I, Fuentes A, et al. Design, generation and stress analysis of face-gear drive with helical pinion[J]. Computer Methods in Applied Mechanics and Engineering, 2005, 194(36-38): 3870-3901. [本文引用:1]

2012

0.0

... 0 引言面齿轮传动是一种锥齿轮与柱齿轮相啮合的新型齿轮传动^[1],当锥齿轮与柱齿轮的回转中心轴正交时,则为正交面齿轮传动,当正交面齿轮副中的面齿轮为正交变传动比面齿轮,柱齿轮为非圆柱齿轮时,为正交变传动比面齿轮传动,简称为正交非圆面齿轮传动 ...

... 目前,国内外还没有开展关于此种新型面齿轮副重合度计算方面的研究工作,极大地阻碍了对该齿轮副的强度,传动特性,动力学等的研究及其在航空航天等领域的应用^[1] ...

... 1 齿轮副的传动原理在正交非圆面齿轮副的传动过程中,具体表现为非圆柱齿轮与非圆面齿轮的节曲线之间的纯滚动^[1],建立如图1所示坐标系 ...

... 3 非圆面齿轮节曲线,齿顶曲线表示根据图1中所示齿轮副的相互运动关系,非圆柱齿轮的随动坐标系 O's-X'sY'sZ's到正交非圆面齿轮的随动坐标系 O'f-X'fY'fZ'f的坐标变换矩阵为^[1]: ...

... 非圆面齿轮的齿顶曲线为半径为 R的圆柱面与非圆面齿轮的齿顶曲面相交形成的空间曲线^[1],非圆面齿轮的齿顶曲面根据非圆面齿轮的加工原理可理解为非圆柱齿轮的齿根曲面的啮合曲面,其在非圆面齿轮随动坐标系 O'f-X'fY'fZ'f中表示为: ...

... 1 齿轮副的齿轮齿条形式及重合度表示正交非圆面齿轮副均由渐开线圆柱齿轮加工而来,在传动过程中,正交非圆面齿轮副实现点接触传动^[1],在其啮合时,总是非圆柱齿轮的齿根与非圆面齿轮的齿顶处进入啮合,非圆柱齿轮的齿顶与非圆面齿轮的齿根处退出啮合,且接触点在非圆柱齿轮节曲线所在截面内^[14],因此可利用机械设计的反转原理,将齿轮副的节曲线与齿顶曲线展开到非圆柱齿轮节曲线所在的固定坐标系中,即将正交非圆面齿轮副传动转换成非圆齿轮齿条传动,见图3 ...

... 当加工非圆齿轮的刀具齿轮的模数确定时,非圆齿轮的齿数变化反映在非圆柱齿轮节曲线的长半轴 a的变化上^[1] ...

2002

0.0

... 正交非圆面齿轮副的重合度是评价该齿轮副的传动连续性,确定轮齿载荷分配系数的依据^[2] ...

2013

0.0

. 2013, 43(4):939-944 DOI:10.7964/jdxbgxb201304016

Moelling of high-spiral bevel gear mesh stiffness based on polynomial

基于多项式的等高齿锥齿轮时变啮合刚度建模

Liu Zhi-feng , Zhang Zhi-min , Zhang Jing-ying

刘志峰, 张志民, 张敬莹

College of Mechanical Engineering and Applied Electronics Technology, Beijing University of Technology, Beijing, 100124,China

We present a new time-varying mesh stiffness model using polynomial function with regard to the time-varying mesh stiffness of the high-bevel gear of a radar device. By analyzing the revolution speed, load torque and damping factor, we build the mesh stiffness model and the nonlinear dynamic equations of the high-bevel gear. We compare the proposed mesh stiffness model with traditional rime-varying mesh stiffness model of multi-order harmonic superposition and reference data model of time-varying comprehensive stiffness. It is shown that, with small damping and overload, the proposed model is much closer to the actual characteristics of the time-varying stiffness. This model lays a foundation to study the gear transmission dynamics, such as vibration damping, noise reduction, smooth transmission and other aspects with small damping and overload.

针对某型雷达装置的等高齿锥齿轮在啮合时的时变啮合刚度,提出一种多项式函数展开的时变啮合刚度新模型。通过转速、负载扭矩、阻尼因子系数分析,构建了多项式函数展开的时变啮合刚度模型,建立了等高齿锥齿轮的非线性动力学方程。将本文建立的时变啮合刚度模型与传统的多阶简谐波叠加形式的时变啮合刚度模型以及综合刚度参考数据模型进行分析对比,发现在小阻尼、重载工况下这种多项式形式的时变啮合刚度模型能更贴近于时变啮合刚度的实际特性,该模型为齿轮传动的减振、降噪、平稳传动等方面的动力学研究打下基础。

... 齿轮副重合度也影响齿轮传动系统的啮合刚度^[3] ...

... P点为非圆柱齿轮与正交变传动比面齿轮节曲线的啮合点, P点的坐标为 (Rθ2,r(0)-r(θ1)),曲线3为非圆柱齿轮的节曲线,曲线4为非圆柱齿轮的齿顶曲线,直线 L1为在 P点处非圆柱齿轮节曲线与正交变传动比面齿轮节曲线的公切线,直线 L2为非圆柱齿轮与非圆面齿轮齿廓啮合点与 P点的线段所在的直线(即瞬时啮合线)^[3],且直线 L1与直线 L2之间的夹角为刀具齿轮的压力角 α0^[3] ...

2013

0.0

... 国内学者针对用渐开线圆柱刀具齿轮加工的非圆柱齿轮进行了重合度方面的研究并提出了计算非圆齿轮重合度的不同方法^[4,5],探索了高重合度弧齿锥齿轮的传动特性^[6],分析了齿轮重合度对齿轮传动系统的动态传动特性的影响^[7] ...

2009

0.0

2003

0.0

2004

0.0

1995

0.0

... 国外研究人员通过加载接触分析,研究了齿轮在真实工况下的承载传动曲线误差和实际重合度,并给出了弧齿锥齿轮传动误差和实际重合度的测量方法与结果^[8,9,10] ...

1998

0.0

1991

0.0

2013

0.0