卡盘定心精度建模及其保持特性与修复方法

引用本文

王健健, 冯平法, 张建富, 吴志军, 张国斌, 闫培龙. 卡盘定心精度建模及其保持特性与修复方法.吉林大学学报:工学版, 2016, 46(2): 487-493
WANG Jian-jian, FENG Ping-fa, ZHANG Jian-fu, WU Zhi-jun, ZHANG Guo-bin, YAN Pei-long. Modeling of centering accuracy of chuck and its maintaining characteristics and restoration method. Journal of Jilin University Engineering and Technology Edition, 2016, 46(2): 487-493 复制到剪切板

Permissions

卡盘定心精度建模及其保持特性与修复方法

王健健^1,², 冯平法^1,², 张建富^1,², 吴志军^1,², 张国斌³, 闫培龙³

1.清华大学机械工程系,北京 100084

2.清华大学精密超精密制造装备及控制北京市重点实验室,北京 100084

3.呼和浩特众环集团, 呼和浩特 010051

通讯作者:冯平法(1966-),男,教授,博士.研究方向:高效精密加工.E-mail:fengpf@mail.tsinghua.edu.com

作者简介:王健健(1988-),男,博士研究生.研究方向:高效精密加工.E-mail:wangjj11@foxmail.com

基金:国家科技重大专项项目(2012ZX04002-061); 摩擦学国家重点实验室基金项目(SKLT2013B03); 北京市科技计划项目(D131100002713003)

摘要

为了提高三爪卡盘的精度保持性,通过建立卡盘定心精度及重复定心精度的计算模型,研究了卡盘主要零部件的磨损对卡盘定心精度的影响及精度修复方法.研究表明:卡盘零部件磨损导致的卡爪位置误差中径向误差是影响定心精度的主要因素;对于楔式三爪动力卡盘而言,重复定心精度的大小等于盘体与楔心套的配合间隙;只有当盘体与楔心套配合间隙的一半小于卡盘定心的系统误差时,才能够通过高爪配车修复卡盘长期使用后的定心精度;磨损引起盘体与楔心套配合间隙增大导致的卡盘精度失效不能通过对高爪进行配车来修复.

关键词: 机床; 三爪卡盘; 定心精度; 磨损; 高爪配车

中图分类号:TH161 文献标志码:A 文章编号:1671-5497(2016)02-0487-07

Modeling of centering accuracy of chuck and its maintaining characteristics and restoration method

WANG Jian-jian^1,², FENG Ping-fa^1,², ZHANG Jian-fu^1,², WU Zhi-jun^1,², ZHANG Guo-bin³, YAN Pei-long³

1.Department of Mechanical Engineering,Tsinghua University, Beijing 100084, China

2.Beijing Key Lab of Precision/Ultra-precision Manufacturing Equipments and Control,Tsinglua University,Beijing 100084,China

3.Huhhot ZhongHuan (Group) Co., Ltd., Huhhot 010051, China

Abstract

To improve the accuracy preservation of three-jaw chuck, the effect of the abrasion of chuck components on its centering accuracy was investigated. The model of centering accuracy and repeatability of three-jaw chuck was developed. Results show that among the position errors of jaws induced by abrasion of chuck components, the radial position error dominates. For the wedge type power chuck, the repeatability accuracy is equal to the interval between chuck body and wedge plunger. Only when the interval between chuck body and wedge plunger is limited within the double systematic error of the centering accuracy, the method of turning top jaw can renovate the centering accuracy after long-term use of the chuck. But the accuracy inefficacy caused by the enlargement of the interval between chuck body and wedge plunger due to the abrasion cannot be renovated by turning the top jaw.

Keyword: machine tool; three-jaw chuck; centering accuracy; abrasion; turning of top jaw

Show Figures

0 引言

高速切削, 硬切削等新型切削技术的发展, 对数控机床的加工精度提出了更高的要求^{[1, 2]}.而电主轴驱动技术的发展^[3]和刀具系统性能的提升^[4], 使工件夹持系统成为阻碍数控车床加工精度提高的薄弱环节^[5].三爪液压动力卡盘由于具有柔性高, 夹紧力大等优点, 是数控车床及车铣复合中心上的主流夹具, 其中以楔式卡盘应用最为广泛.与工件和主轴直接相连相比, 卡盘的夹持势必会对工件的尺寸和形状加工精度产生不利影响^[6].理想的卡盘应该时刻保证工件待加工表面的"理论轴线"与机床的回转轴线相重合, 这种重合的准确程度称为卡盘的定心精度^[7].对于一般的轴类工件而言, 待加工表面的理论轴线就是被夹持工件表面的几何轴线.卡盘定心误差的存在会导致圆柱工件已加工表面与未加工表面之间的同轴度误差^[8].影响卡盘定心精度的因素有很多, 例如几何误差, 高爪成型模具的倾斜, 主定位面的选择^[9], 卡爪/工件的接触变形, 动态冗余度^[10]等, 而卡盘零部件的制造误差, 磨损造成的卡爪几何误差是其中最基本的因素^[11].卡盘零部件的制造误差可以通过优化卡盘的制造公差, 对软爪进行配车等方法来减小或者消除^[12].卡盘零部件的磨损是在卡盘的使用中逐渐出现的, 直接关系到卡盘的精度可靠性^[13].目前, 针对卡盘零部件磨损对定心精度影响的研究还停留在定性阶段, 由于缺乏必要的理论计算, 这些研究不能满足卡盘的精度可靠性设计中对定量计算方法的迫切需求.

本文通过建立卡盘几何定心精度的理论计算模型, 研究了零部件磨损对卡盘定心精度的影响规律, 并对零部件磨损后的卡盘定心精度修复问题进行了理论分析.

1 卡盘定心精度理论建模

三爪卡盘的定心精度可以用三爪所夹持工件的几何轴线(即夹持中心)与机床主轴回转中心的接近程度来度量, 两者之间差距越小, 说明定心精度越高.

1.1 夹持中心的向量表示方法

理想三爪卡盘的三个卡爪夹持弧的位置应该严格中心对称, 且对称中心在主轴的轴线上.当卡盘由于零件磨损引起单爪或多爪夹持弧的位置存在误差而导致三爪位置不对称时, 则会出现定心误差.

如图1所示, 设点O为主轴回转中心, W_i 为三爪完全中心对称时的卡爪i夹持弧位置, R为三爪位置无误差时所夹持工件的半径, 即 $| \vec{O W_{i}} |= R$ . $W'_{i}$ 为存在误差时卡爪i的夹持弧位置, Δ R_i 为卡爪i的径向位置误差, Δ C_i 为卡爪i的周向位置误差.O'为 $△ W'_{1} W'_{2} W'_{3}$ 外接圆的圆心, 即卡爪位置存在误差时三爪的夹持中心.三个矢量 $\vec{O W_{1}} 、 \vec{O W_{2}} 、 \vec{O W_{3}}$ 夹角互为120° , → _i 为 $\vec{O W_{i}}$ 方向的单位向量.

	Figure Option View Download New Window
	图1 三爪位置存在误差时的夹持中心示意图Fig.1 Diagram of clamping center when three jaws possess a position error

1.1.1 单爪径向位置存在误差时, 夹持中心的向量表示方法

图2为卡盘的一个爪(爪1)的径向位置存在大小为Δ R₁ 的误差, 导致与另外两爪位置不对称时的夹持中心计算示意图.图中, G₁ O'为线段W'₁ W₂ 的垂直平分线, W'₂ 与W₂ 重合, W'₃ 与W₃ 重合, 并有 $| \vec{W_{1} W'_{1}} | = Δ R_{1}$ .

	Figure Option View Download New Window
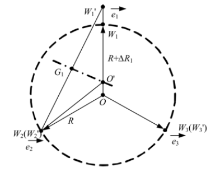	图2 单爪径向位置存在误差时夹持中心计算示意图Fig.2 Calculation of clamping center when a single jaw possesses a radial position error

在△ OO'W₂ 中, $\begin{matrix} | \vec{O' W_{2}} |= R + Δ R_{1} - | \vec{OO'} |, \end{matrix}$ 由余弦定理得到:

$\begin{matrix} \begin{matrix} (R + Δ R_{1} {- | \vec{OO'} |)}^{2} = \\ R^{2} + | \vec{OO'} |^{2} - 2 R | \vec{OO'} | \cos 120 ° \end{matrix} \end{matrix}$ (1)

对式(1)进行化简变形, 得到:

$\begin{matrix} | \vec{OO'} |= \frac{2 Δ R_{1}}{3} \cdot \frac{1 + 0.5 \frac{Δ R_{1}}{R}}{1 + \frac{2 Δ R_{1}}{3 R}} \end{matrix}$ (2)

一般卡盘的径向位置误差不会很大, 即 $\begin{matrix} Δ R_{1} ≪ R, \end{matrix}$ 则可以得到:

$\begin{matrix} \frac{1 + 0.5 \frac{Δ R_{1}}{R}}{1 + \frac{2 Δ R_{1}}{3 R}} \approx 1 \end{matrix}$ (3)

由式(2)(3)可知, 卡盘单爪的径向位置存在误差 $\begin{matrix} Δ R_{1} \end{matrix}$ 时三爪夹持中心的向量表示公式为:

$\begin{matrix} \vec{OO'} = \frac{2 Δ R_{1}}{3} {e \vec{\to}}_{i} \end{matrix}$ (4)

1.1.2 单爪周向位置存在误差时, 夹持中心的向量表示方法

图3为卡盘一个爪(爪1)的周向位置存在大小为Δ C₁ 的误差, 导致与另外两爪不对称时的夹持中心计算示意图.图中, G₂ O'为线段W'₁ W₂ 的垂直平分线, W'₂ 与W₂ 重合, W'₃ 与W₃ 重合, 并有 $| \vec{W_{1} W'_{1}} | = Δ C_{1}$ .

	Figure Option View Download New Window
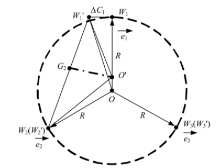	图3 单爪周向位置存在误差时夹持中心计算示意图Fig.3 Calculation of clamping center when a single jaw possesses a circumferential position error

在 $\begin{matrix} △ OO' W_{2} \end{matrix}$ 中:

$\begin{matrix} | \vec{O' W_{2}} |= \sqrt[]{{(R - | \vec{OO'} |)}^{2} + Δ C_{1}^{2}}, \end{matrix}$

由余弦定理可知:

$\begin{matrix} \begin{matrix} {(R - | \vec{OO'} |)}^{2} + Δ C_{1}^{2} = \\ R^{2} + | \vec{OO'} |^{2} - 2 R | \vec{OO'} | \cos 120 ° \end{matrix} \end{matrix}$ (5)

将式(5)化简得到:

$\begin{matrix} | \vec{OO'} |= \frac{Δ C_{1}^{2}}{3 R} \end{matrix}$ (6)

由于 $\begin{matrix} Δ C_{1} ≪ R, \end{matrix}$ 所以:

$\begin{matrix} | \vec{OO'} | = 0 \end{matrix}$ (7)

由以上分析可知, 卡盘零部件磨损导致的卡爪径向位置误差对其定心精度有较大影响, 而磨损导致的卡爪周向位置误差对其定心精度影响非常小.因此, 在后文的分析中忽略卡爪的周向位置误差对卡盘定心精度的影响.

1.1.3 两个及以上卡爪的径向位置存在误差时, 夹持中心的向量表示方法

图4为两个及以上卡爪的径向位置存在误差, 导致三爪的径向位置互不对称时夹持中心的计算示意图.图中O″为△ W'₁ W₂ W₃ 外接圆的圆心, G₃ O″为线段W'₁ W₃ 的垂直平分线, 并且有 $| \vec{W_{1} W'_{1}} | = Δ R_{1}, | \vec{W_{2} W'_{2}} | = Δ R_{2}$ .

	Figure Option View Download New Window
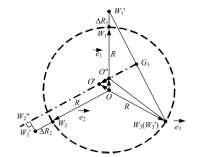	图4 多爪径向位置存在误差时夹持中心计算示意图Fig.4 Calculation of clamping center when two jaws possess radial position errors

由1.1.1和1.1.2节的分析可以得到:

$\begin{matrix} \{\begin{matrix} | \vec{OO″} |= \frac{2 Δ R_{1}}{3} \\ | \vec{O″W'_{2}} |= R + Δ R_{2} + | \vec{OO'} | \sin 30 ° \\ | \vec{O″W'_{1}} |= R + Δ R_{1} + | \vec{OO'} | \end{matrix} \end{matrix}$ (8)

由式(8)可以得到:

$\begin{matrix} | \vec{O″W'_{2}} |-| \vec{O″W'_{1}} | = Δ R_{2} \end{matrix}$ (9)

进而得到:

$\begin{matrix} | \vec{O'O″} |= \frac{2 Δ R_{2}}{3} \end{matrix}$ (10)

由式(8)和式(10)得到:

$| \vec{OO'} |= \frac{2}{3} (Δ R_{1} {e \to}_{1} + Δ R_{2} {e \to}_{2})$ (11)

由于:

$\{\begin{matrix} Δ R_{1} = | \vec{OW'_{1}} |-| \vec{OW'_{3}} | \\ Δ R_{2} = | \vec{OW'_{2}} |-| \vec{O W'_{3}} | \end{matrix}$ (12)

将式(12)代入到式(11), 得到卡盘三爪径向位置不对称时, 三爪夹持中心的向量表示公式:

$\begin{matrix} | \vec{OO'} |= \frac{2}{3} \sum \vec{OW'_{1}} \end{matrix}$ (13)

由式(13)可知, 三爪的卡盘定心精度可以用3个卡爪径向位置向量相加后乘以系数2/3得到.根据向量的可加性, 每种因素对卡盘定心精度的影响可以单独分析.

1.2 重复定心误差的理论分析

在影响单个卡盘的几何定心精度的众多因素中, 有些因素(例如磨损导致的卡爪尺寸误差)在一定时间内单个卡盘重复夹持工件时是不变的, 这些因素引入的是系统误差; 有些因素(例如卡盘零部件的配合间隙引起的卡爪径向和周向窜动)在单个卡盘重复夹持工件时是变化的, 使卡盘在重复多次夹持同一工件时, 夹持中心的位置并不完全一致, 这些因素引入的是随机的重复定心误差.

三爪卡盘的重复定心精度是指单个卡盘的三爪多次夹持工件的几何轴线之间的接近程度, 这些几何轴线之间的差距越小, 说明重复定心精度越高.卡盘的定心精度是系统误差和随机误差的综合表征, 决定着单件工件的加工精度; 而重复定心精度一般只与随机误差有关, 决定着批量加工工件的一致性.

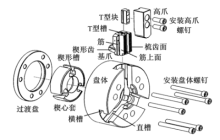
图5为楔式动力卡盘的结构示意图.楔式动力卡盘由盘体, 过渡盘, 楔心套, 基爪, T型块和高爪等零部件组成.

	Figure Option View Download New Window
	图5 楔式动力卡盘的结构图Fig.5 Structure of wedge type power chuck

如图5所示, 卡盘夹紧系统里存在的主要配合间隙有:过渡盘外圆与盘体止口的间隙, 盘体横槽与基爪筋的间隙, 盘体直槽与基爪筋上面的间隙, T型块与基爪和高爪的配合间隙, 盘体内圆与楔心套外圆的间隙.其中过渡盘外圆与盘体止口的间隙引起的卡盘安装误差对于已经安装在机床上单个卡盘来说是不变的系统误差; 盘体横槽与基爪筋的间隙在卡盘夹紧工件时由于基爪的倾转也会消除, 这一间隙引起的定心误差对于单个卡盘来说也是不变的系统误差; 盘体直槽与基爪筋上面的配合间隙, 以及T型块与基爪和高爪的配合间隙, 则会引起基爪的周向位置, 表现出不确定性, 但是由1.1.2节可知, 这种不确定性对卡盘的定心精度的影响很小; 而盘体内圆与楔心套外圆之间的间隙, 则会导致楔心套的径向位置的窜动, 进而引起基爪径向位置的不确定性, 最终导致卡盘的重复定心误差.

图6为在不考虑系统误差时楔心套与盘体的配合间隙引起卡盘重复定心误差的示意图.图中点O表示盘体内圆轴线, 与机床主轴轴线重合.圆O的直径等于盘体与楔心套的配合间隙d_cx. $\vec{{| M}_{i} W_{i}} |$ 表示楔心套三口到卡爪夹持弧的径向尺寸, $\vec{M_{i} W_{i}}$ 互成120° 角且长度相等.A表示楔心套外圆的轴线, $\vec{A N_{i}}$ 表示楔心套三个楔形口的径向尺寸, 三个向量 $\vec{A N_{i}}$ 互成120° 角且长度相等. $\vec{M_{i} W_{i}} 与 \vec{A N_{i}}$ 相互平行.

	Figure Option View Download New Window
	图6 楔心套与盘体的配合间隙引起卡盘重复定心误差Fig.6 Calculation of repeatability accuracy induced by the existence of the interval between chuck body and wedge plunger

图6中, A在圆O内, 则向量点 $\begin{matrix} \vec{OA} \end{matrix}$ 应满足:

$\begin{matrix} \vec{OA} \leq d_{cx} / 2 \end{matrix}$ (14)

则在系统误差为零时, 由式(13)可得夹持中心的向量计算公式为:

$\begin{matrix} \vec{OO'} = \frac{2}{3} \sum (\vec{OA} \cdot {e \vec{\to}}_{i}) {e \vec{\to}}_{i} \end{matrix}$ (15)

式中: $\begin{matrix} \vec{OA} \cdot e \to_{i} \end{matrix}$ 为楔心套的外圆轴线与盘体内圆轴线不重合时引起的卡爪i的径向位置误差.

将 $\begin{matrix} < {e \to}_{i}, {e \vec{\to}}_{i} > = 120 °, i \neq j \end{matrix}$ 代入到式(15)中, 化简得到:

$\begin{matrix} \vec{OO'} = \vec{OA} \end{matrix}$ (16)

即点A和点O'重合, 楔心套外圆的轴线与三爪夹持中心重合.

由式(14)和式(16)得到:

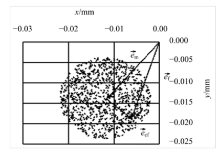
$\begin{matrix} \vec{OO'} \leq d_{cx} / 2 \end{matrix}$ (17)

为了表示楔式三爪卡盘的重复定心精度与定心精度的关系, 采用蒙特卡洛法^[14]模拟单个卡盘重复夹持标准工件1000次, 得到夹持中心的坐标数据图, 如图7所示.图7所用的坐标系建立在机床主轴上, 坐标平面垂直于机床主轴轴线, 原点与机床主轴轴线重合, x轴与盘体某一直槽的中心平面相平行.d_cx取值为0.02 mm, 系统误差为0.018 mm.图中e → _m 为散点圆的圆心位置向量, 由系统误差决定; e → _ef 为某一个散点相对于散点圆圆心的位置矢量, 由随机误差决定; e → _f为夹持中心相对于主轴轴线的位置矢量.

	Figure Option View Download New Window
	图7 单个卡盘重复夹持工件获得的工件轴线坐标散点图Fig.7 Scatter diagram of clamping center of a single chuck

由图7可知, 单个卡盘重复夹持工件获得的工件轴线坐标的散点分布区域是一个圆.由于卡盘的重复定心精度表示的是定心精度的离散程度, 因此图7中的散点圆的直径等于卡盘的重复定心精度.图7中圆的直径为0.02 mm, 与楔心套与盘体配合间隙的大小相等, 结合式(17)可知:楔式三爪动力卡盘的重复定心精度在数值上等于盘体与楔心套配合间隙的大小.

2 零部件磨损量与定心精度的关系

卡盘零部件的磨损一方面会使卡爪的尺寸产生误差, 引入系统性误差, 这些误差在卡盘多次重复夹持工件时总是存在, 且大小不变; 另一方面会使零部件的配合间隙增大, 特别是盘体与楔心套配合间隙的增大, 从而引入随机性的重复定心误差, 这些误差在卡盘多次重复夹持工件时, 会随着楔心套外圆轴线与盘体内圆轴线的相对位置的变化而变化.

图8为夹紧状态下盘体, 楔心套和基爪等卡盘主要零部件应力分布的有限元分析结果.

	Figure Option View Download New Window
	图8 卡盘各主要零部件应力分布图Fig.8 Stress diagram of chuck components

由图8可知:在卡盘夹紧工件时, 卡盘主要零部件之间的接触并不均匀, 这主要是由于卡爪在夹紧力的作用下发生倾转造成的.

对于盘体横槽和基爪筋的接触而言, 应力最大处发生在接触面沿卡盘径向方向的两端, 相应的磨损会使盘体横槽与基爪筋的配合间隙增大, 设增大量为Δ d_{1, i}, 则引起的爪i的径向误差ε _{1, i}为:

$\begin{matrix} ε_{1, i} = Δ d_{1, i} \frac{L_{h}}{L_{b}} \end{matrix}$ (18)

式中:L_h为卡盘的夹持中心高, 表示夹紧力作用点到基爪筋中心平面的距离; L_b为基爪的筋沿卡盘径向方向的长度.

由式(18)可知, 卡盘在长时间服役后应避免使用过大的夹持中心高, 以降低基爪筋与盘体横槽配合间隙的增大对定心精度的不利影响.

楔心套的最大应力发生在楔型槽的远主轴端, 会使爪i对应的楔型槽径向尺寸产生误差Δ d_{2, i}, 引起的单爪径向误差ε _{2, i}为:

$\begin{matrix} ε_{2, i} = Δ d_{2, i} \end{matrix}$ (19)

楔心套和基爪的接触不均匀使楔角变小, 变化量为Δ α _i, 则由泰勒公式可以得到楔角变小引起的单爪径向误差ε _{3, i}为:

$\begin{matrix} ε_{3, i} = ΔSse c^{2} αΔ α_{i} \end{matrix}$ (20)

式中:Δ S为卡盘夹紧工件时楔心套的轴向位移.

高爪i夹持弧的径向磨损量Δ d_{4, i} 会直接导致单爪的径向位置误差ε _{4, i}为:

$\begin{matrix} ε_{4, i} = Δ d_{4, i} \end{matrix}$ (21)

则卡盘定心误差中系统误差的总变化量 $\begin{matrix} \vec{ε} \end{matrix}$ '_m为:

$\begin{matrix} \vec{ε}'_{m} = \sum_{i} (\overset{4}{\sum_{k}} ε_{k, i}) e \to_{i} \end{matrix}$ (22)

盘体与楔心套配合间隙增大为d'_cx, 则卡盘定心误差中随机误差的最大值ε '_cf变为:

$\begin{matrix} ε'_{cf} = d'_{cx} / 2 \end{matrix}$ (23)

3 高爪配车修复卡盘定心精度

对卡爪进行配车是修复卡盘长时间服役后精度的重要方法.生产中一般会用高爪预先夹持一个配车环, 然后在高爪上车出一个与工件相同直径的夹持弧, 如图9所示.

	Figure Option View Download New Window
	图9 卡爪配车示意图Fig.9 Turning of the top jaws

	Figure Option View Download New Window
	图10 配车过程误差传递示意图Fig.10 Error propagation of turning top jaws

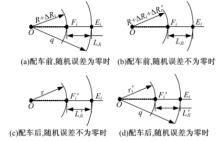
图10为配车过程的误差传递示意图, 图中E_i 表示卡爪i上某一个固定的点, 在随机误差为零(即楔心套的轴线与盘体内圆的轴线重合)时, 该点到O点(主轴回转中心)距离等于定值q.图10(a)和图10(b)分别表示对卡爪进行配车前随机误差为零时和不为零时的卡爪径向位置误差情况.图中F_i 为配车前卡爪夹持弧的径向位置, L_Ji 为F_i 点到E_i 点的径向距离, Δ R_i 为爪i夹持弧的径向位置系统误差, Δ R'_i 为爪i夹持弧的径向随机误差.图10(c)和图10(d)分别表示对卡爪进行配车后, 随机误差不为零时和为零时的卡爪径向位置误差情况示意图.其中, 图10(c)与图10(b)中的楔心套外圆轴线与盘体内圆轴线的相对位置相同.图10(c)中, r为卡爪配车出的夹持弧半径, F'_i 为爪i配车后的夹持弧径向位置, L'_Ji 为F'_i 点到E_i点的径向距离.图10(d)中, r'_i 为随机误差为零时F'_i 点到O点的距离.

由图10(a)可以得到:

$\begin{matrix} R + Δ R_{i} + L_{Ji} = q \end{matrix}$ (24)

由图10(b)和图10(c)可以得到:

$\begin{matrix} r + L'_{Ji} = R + Δ R_{i} + ΔR'_{i} + L_{Ji} \end{matrix}$ (25)

由图10(d)可以得到:

$\begin{matrix} r'_{i} + L'_{Ji} = q \end{matrix}$ (26)

由式(24)~(26)可以得到:

$\begin{matrix} r'_{i} = r - ΔR'_{i} \end{matrix}$ (27)

则高爪配车后卡盘定心误差中系统误差ε _{m, t}为:

$\begin{matrix} ε_{m, t} = | \frac{2}{3} \sum r'_{i} {\vec{e}}_{i} |= \frac{2}{3} | \sum ΔR'_{i} {e \vec{\to}}_{i} | \end{matrix}$ (28)

由式(28)可知, 对卡爪进行配车, 只能消除卡盘零部件磨损导致的系统误差, 而盘体和楔心套配合间隙引起的卡爪径向位置随机误差在配车后会转化为系统误差.因此, 由于磨损导致楔心套外圆和盘体内圆配合间隙增大引起的卡盘精度失效无法通过配车方法来修复.

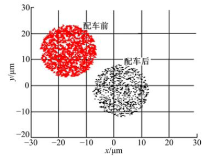
图11为一定系统误差(0.022 mm)下, 蒙特卡洛法^[14]模拟获得的卡盘配车前后重复夹持中心分布示意图, 其坐标系与图7相同.

	Figure Option View Download New Window
	图11 高爪配车前后的夹持中心散点图Fig.11 Scatter diagram of clamping center before and after turning the top jaws

由图11可知, 单个卡盘配车后重复夹持工件获得的工件轴线坐标的散点分布区域也是一个圆.与该卡盘配车前的散点圆相比, 两个散点圆的直径相同, 另外, 卡盘配车后的散点圆整体上更加接近坐标原点, 但不与坐标原点重合.因此, 图11进一步说明了式(28)的结果, 对高爪配车能够有效修复卡盘长时间服役后零部件磨损引起的精度降低, 但是只能部分消除系统误差, 对盘体与楔心套的配合间隙导致的随机误差无能为力.

结合式(14)(15)(16)可以得到:

$\begin{matrix} ε_{m, t} \leq d'_{cx} / 2 \end{matrix}$ (29)

则由式(23)和式(29)在高爪通过配车修复精度后, 卡盘的定心精度e_{f, t}为:

$\begin{matrix} e_{f, t} = ε_{m, t} + ε'_{cf} \leq d'_{cx} \end{matrix}$ (30)

由式(30)可知, 卡盘在对高爪配车后的定心精度总小于盘体与楔心套的配合间隙.

由式(29)和(30)可知, 要使高爪配车后的精度得到修复, 需要满足以下关系:

$\begin{matrix} d'_{cx} / 2 \leq ε_{m} \end{matrix}$ (31)

式中: $\begin{matrix} ε_{m} \end{matrix}$ 为配车前的系统误差.

由式(31)可知, 只有当盘体与楔心套的配合间隙足够小(小于系统误差的两倍)时才能通过对高爪配车来修复卡盘的定心精度, 因此生产中要特别注意盘体与楔心套配合处的润滑与防尘.

4 结论

(1)卡盘零部件磨损导致的卡爪径向位置误差对卡盘定心精度的影响很大, 而周向位置误差对卡盘定心精度的影响很小.对于楔式三爪动力卡盘而言, 其重复定心精度大小等于盘体与楔心套的配合间隙.

(2)盘体与楔心套配合间隙导致的随机误差会在配车时转化为系统误差, 因此对高爪重新配车只能消除部分系统误差.只有当盘体和楔心套配合间隙足够小(小于系统误差的两倍)时, 才能通过高爪配车修复卡盘长期使用后的定心精度.

(3)对高爪进行配车修复后的卡盘定心精度总小于盘体与楔心套配合间隙; 磨损引起盘体与楔心套配合间隙增大导致的卡盘精度失效不能通过对高爪进行配车来修复.

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Fnides B, Aouici H, Yallese M A. Cutting forces and surface roughness in hard turning of hot work steel X38CrMoV5-1 using mixed ceramic[J]. Mechanika, 2008, 2(70): 73-78. [本文引用:1]
[2]	Zhou J M, Andersson M, Ståhl J E. Identification of cutting errors in precision hard turning process[J]. Journal of Materials Processing Technology, 2004, 153: 746-750. [本文引用:1]
[3]	胡志栋, 姜继海, 戴达军, 等. 动力卡盘对数控机床加工精度的影响[J]. 现代制造工程, 2009(8): 4-9. Hu Zhi-dong, Jiang Ji-hai, Dai Da-jun, et al. Research on the effect of power chuck on the machining precision of numerical control machine tool[J]. Modern Manufacturing Engineering, 2009(8): 4-9. [本文引用:1]
[4]	Ventura C E H, Köhler J, Denkena B. Cutting edge preparation of PCBN inserts by means of grinding and its application in hard turning[J]. CIRP Journal of Manufacturing Science and Technology, 2013, 6(4): 246-253. [本文引用:1]
[5]	Byun J, Liu C R. Methods for improving chucking accuracy[J]. Journal of Manufacturing Science and Engineering, 2012, 134(5): 051004. [本文引用:1]
[6]	Sölter J, Grote C, Brinksmeier E. Influence of clamping strategies on roundness deviations of turned rings[J]. Machining Science and Technology, 2011, 15(3): 338-355. [本文引用:1]
[7]	周城. 数控机床高速液压动力卡盘的研究[D]. 杭州: 浙江大学机械电子工程系, 2011. Zhou Cheng. Research on high speed hydraulic power chuck for CNC machine tools[D]. Hangzhou: Department of mechanical Engineering, Zhejiang University, 2011. [本文引用:1]
[8]	Byun J. Methods for improving chucking accuracy of a cylindrical workpiece in finish hard turning[D]. Indianapolis: Purdue University, 2003. [本文引用:1]
[9]	Byun J, Liu C R. Selection of major locating surface for improving chucking accuracy[C]//International Manufacturing Science and Engineering Conference. Indiana, USA: ASME, 2009: 489-497. [本文引用:1]
[10]	Byun J, Liu C R. Improving chucking accuracy and reeatability by reducing kinematic redundancy[J]. Journal of Manufacturing Science and Engineering, 2010, 132(6): 064501. [本文引用:1]
[11]	Solaja V, Malajdzic M. Some experiments with three and four jaw chucks[J]. Annals of the CIRP, 1968, 16: 131-136. [本文引用:1]
[12]	王健健, 张建富, 冯平法, 等. 楔式动力卡盘静态夹持精度建模与综合[J]. 西安交通大学学报, 2013, 47(3): 90-95. Wang Jian-jian, Zhang Jian-fu, Feng Ping-fa, et al. Modeling and optimizing of static chucking accuracy of power-operated wedge hook chuck[J]. Journal of Xi'an Jiaotong University, 2013, 47(3): 90-95. [本文引用:1]
[13]	龚俊, 汤文成, 韦鸣, 等. 高速精密动力卡盘的失效形式分析研究[J]. 中国制造业信息化, 2012(3): 70-73, 76. Gong Jun, Tang Wen-cheng, Wei Ming, et al. A study on failure mode analysis of high-speed and high-precision power chucks[J]. Manufacture Information Engineering of China, 2012(3): 70-73, 76. [本文引用:1]
[14]	Metropolis Ni, Stanislaw U. The monte carlo method[J]. Journal of the American Statistical Association, 1949, 44(247): 335-341. [本文引用:2]

2008

0.0

... 0 引言高速切削,硬切削等新型切削技术的发展,对数控机床的加工精度提出了更高的要求^[1,2] ...

2004

0.0

... 0 引言高速切削,硬切削等新型切削技术的发展,对数控机床的加工精度提出了更高的要求^[1,2] ...

2009

0.0

. 2009, (8):4-9 DOI:doi:10.3969/j.issn.1671-3133.2009.08.002

Research on the effect of power chuck on the machining precision of numerical control machine tool

Hu Zhi-dong , Jiang Ji-hai , Dai Da-jun

胡志栋, 姜继海, 戴达军

数控机床主轴的精度直接影响数控机床的加工精度,目前其转速要求越来越高,现有的机床附件--动力卡盘与主轴的高转速形成了矛盾,其中安全和精度是首先要考虑的因素.分析了动力卡盘对加工精度的影响,针对回转油缸配流问题对提高动力卡盘转速的限制,将配流副的问题归结为端面油膜密封技术问题,为动力卡盘的高速化提供了参考,也为数控机床高速切削下的加工精度问题提供了解决途径.

... 而电主轴驱动技术的发展^[3]和刀具系统性能的提升^[4],使工件夹持系统成为阻碍数控车床加工精度提高的薄弱环节^[5] ...

2013

0.0

... 而电主轴驱动技术的发展^[3]和刀具系统性能的提升^[4],使工件夹持系统成为阻碍数控车床加工精度提高的薄弱环节^[5] ...

2012

0.0

... 而电主轴驱动技术的发展^[3]和刀具系统性能的提升^[4],使工件夹持系统成为阻碍数控车床加工精度提高的薄弱环节^[5] ...

2011

0.0

... 与工件和主轴直接相连相比,卡盘的夹持势必会对工件的尺寸和形状加工精度产生不利影响^[6] ...

2011

0.0

. 2011, :-

Research on high speed hydraulic power chuck for CNC machine tools

数控机床高速液压动力卡盘的研究[D]

Zhou Cheng.

周城

高档数控机床的高速高精度发展趋势,对数控机床的功能部件提出了更高的速度与精度要求,液压动力卡盘作为数控车床和车铣复合加工中心的重要功能部件,向着高转速和高夹持精度方向发展。然而,高速液压动力卡盘的发展相对落后于电主轴和切削刀具等其它功能部件,缺乏高速、安全的液压动力卡盘已成为高速车削技术未能在批量生产中得到广泛应用的一个重要原因；我国的液压动力卡盘技术落后于欧洲和日本,高档液压动力卡盘全部进口。本学位论文研究高速液压动力卡盘的高速回转密封和夹紧力损失补偿等关键技术,目的在于提高液压动力卡盘的转速性能,并为液压动力卡盘的结构设计和优化提供理论参考,为其性能检测提供手段,具有重要的工程意义和学术研究价值。本文创建了回转液压缸多段微米级密封缝隙的液固气三相热耦合流动数值模型,该模型考虑了液压油液的粘温特性、油液与固体壁面和空气之间的热传递、以及三个密封缝隙之间的相互传热,因此对油液温度的预测效果比经典的缝隙流动理论更加准确,而且还能预测固体圆环的壁面温度,计算与实验结果对比表明,该模型计算的油液温度误差小于5%内,可为高速回转液压缸回转密封的设计提供理论基础。提出了高速动力卡盘的夹紧力损失分段模型,该模型考虑了动力卡盘传动机构在低速阶段与高速阶段的变形差异、卡盘传动机构的摩擦力、回转液压缸中液压油液的压缩性等因素,更深入地揭示了高速动力卡盘的夹紧力损失机理,与实验结果对比表明,该模型计算的夹紧力损失尤其是夹紧力损失系数,比已有的夹紧力损失模型具有更高的精度。据此研制的外径250mm和160mm两种规格的离心力补偿型高速动力卡盘样机,填补了国内空白。样机的大量试验结果表明,外径250规格的动力卡盘在6000rpm时的剩余夹紧力是初始夹紧力的82.9%,外径 160规格的动力卡盘在7500rpm时的剩余夹紧力是初始夹紧力的71.5%,远高于行业标准规定的33%,剩余夹紧力和转速达到目前国际量产动力卡盘的最好指标。发明了一种高转速拉压力传感器,该传感器将应变式拉压力测量技术与非接触式供电和信号传输技术结合为一体,能够在高转速时测量回转液压缸的输出推拉力,解决了高转速工况下回转液压缸的保压性能检测难题,为回转液压缸及其液压锁的性能改进提供了有效的检测手段。论文主要结构如下：第一章,介绍液压动力卡盘的发展历程、关键技术问题和国内外研究现状,论述了本文的研究目的、意义和主要研究内容。第二章,建立了回转液压缸全周口密封缝隙流动和温升的理论模型,以及三段微米级密封缝隙的液固气三相热耦合流动的数值模型,并开展了实验研究；分析了全周口缝隙流动的温升、热传递和泄漏量等特性,提出了降低缝隙流动温升的措施；开展了非全周口密封缝隙流动的温升、泄漏量和转矩的实验研究。第三章,建立了楔式动力卡盘的静态夹紧力模型,分析了楔式动力卡盘的传动效率；建立了楔式动力卡盘的夹紧力损失分段模型,并分析了摩擦力、刚度和结构尺寸对夹紧力损失的影响。第四章,建立了杠杆式补偿型动力卡盘的夹紧力损失模型,并提出了夹紧力损失的优化设计方法,研制了杠杆式补偿型动力卡盘样机；提出了基于电液比例压力控制和压力多级控制的夹紧力控制方法。第五章,介绍了高转速拉压力传感器的工作原理,分析了离心力对传感器测量精度的影响,提出了膨胀变形引起的测量误差的补偿方法。论述了高转速拉压力传感器在液压动力卡盘中的应用。第六章,总结本文的研究工作,归纳了主要的研究结论,指出论文的创新点,并对今后的研究工作进行展望。

... 理想的卡盘应该时刻保证工件待加工表面的"理论轴线"与机床的回转轴线相重合,这种重合的准确程度称为卡盘的定心精度^[7] ...

2003

0.0

... 卡盘定心误差的存在会导致圆柱工件已加工表面与未加工表面之间的同轴度误差^[8] ...

2009

0.0

... 影响卡盘定心精度的因素有很多,例如几何误差,高爪成型模具的倾斜,主定位面的选择^[9],卡爪/工件的接触变形,动态冗余度^[10]等,而卡盘零部件的制造误差,磨损造成的卡爪几何误差是其中最基本的因素^[11] ...

2010

0.0

1968

0.0

2013

0.0

. 2013, 47(3):90-95 DOI:doi:10.7652/xjtuxb201303017

Modeling and optimizing of static chucking accuracy of power-operated wedge hook chuck

楔式动力卡盘静态夹持精度建模与综合

Wang Jian-jian , Zhang Jian-fu , Feng Ping-fa

王健健, 张建富, 冯平法

摘　要：为了提高液压动力卡盘的设计及制造精度，基于小位移旋量的方法，考虑4个精度指标及9项一致性的因素后，采用多体理论建立了楔式动力卡盘的静态夹持精度模型。基于该模型，采用蒙特卡罗方法对批量生产条件下的卡盘的静态夹持精度、单个卡盘的重复静态夹持精度，以及高爪配车后的定心精度进行了分析，定量地阐述了各因素对卡盘静态夹持精度的影响程度，进而针对线性化处理后的精度模型，以成本最小化为目标函数，提出了使用遗传算法进行精度综合的方法。研究表明，对于型号为KT55200的卡盘，当楔心套和盘体的配合间隙控制在10μm以内时，高爪配车才能有效提高卡盘的重复定心精度，通过一致性控制向量寻优进行精度综合，可降低19％的生产成本。

... 卡盘零部件的制造误差可以通过优化卡盘的制造公差,对软爪进行配车等方法来减小或者消除^[12] ...

2012

0.0

. 2012, (3):70-73,76 DOI:doi:10.3969/j.issn.1672-1616.2012.03.019

A study on failure mode analysis of high-speed and high-precision power chucks

Gong Jun , Tang Wen-cheng , Wei Ming

龚俊, 汤文成, 韦鸣

对高速精密动力卡盘的失效形式进行了分析研究,提出了避免在预定寿命期内失效的要求,建立了失效鱼骨图.分析动力卡盘的材料选择和热处理技术、摩擦磨损和精度对动力卡盘失效的影响,对卡盘的优化设计和应用以及夹紧力计算具有指导意义.

... 卡盘零部件的磨损是在卡盘的使用中逐渐出现的,直接关系到卡盘的精度可靠性^[13] ...

1949

0.0

... 为了表示楔式三爪卡盘的重复定心精度与定心精度的关系,采用蒙特卡洛法^[14]模拟单个卡盘重复夹持标准工件1000次,得到夹持中心的坐标数据图,如图7所示 ...

... 022 mm)下,蒙特卡洛法^[14]模拟获得的卡盘配车前后重复夹持中心分布示意图,其坐标系与图7相同 ...